基于内积矩阵及深度学习的结构健康监测研究

王 慧，郭晨林，王 乐，张敏照

(1.长安大学理学院，西安 710064；2.西北工业大学航空学院，西安 710072；3.上海交通大学航空航天学院，上海 200240)

基于振动的结构健康监测方法因其容易实现在线监测，一直以来受到国内外研究者的广泛关注。根据结构健康监测是否需要建立准确的结构理论模型，基于振动的结构健康监测方法可分为基于模型的方法及不基于模型的方法[1]。基于模型的方法一般为基于有限元模型修正的方法，其计算过程直观、物理意义明确[2]。对于较为复杂的结构，一般不容易建立其准确的理论模型，因此不基于模型的方法更容易应用于复杂结构的健康监测。不基于模型的方法一般利用结构时域响应、频域响应或模态参数及其组合[3-5]，并结合相关数据处理方法，建立结构振动响应特征量与结构健康状态的对应关系。可以看出，数据处理在不基于模型的方法中有着至关重要的作用；同时，针对实际工程结构的健康监测往往涉及大量的测试数据。因此基于大数据及深度学习思想的结构健康监测研究是该领域的一个发展方向[6-7]。

深度学习作为一种更容易实现人工智能的机器学习方法，近些年来首先在计算机视觉、语音识别、自然语言处理等领域取得了显著的成效[8]。深度学习的本质是通过深层次特征提取来获取数据特征，因此在与数据处理相关的其他领域也开始受到关注，如数据检测[9]、优化设计[10]、机械/结构健康监测[11]等多个领域。在结构健康监测领域，目前基于深度学习的方法主要从两个方面开展研究：一类基于图像识别的方法；另一类是基于振动响应信号处理的方法。

基于图像识别的方法也称计算机视觉，通过对结构局部照片图像进行特征提取并识别其健康状态[12]，一般监测的均为结构表面裂纹、表面腐蚀等结构表面损伤，其本质属于图像识别，且广泛采用的是卷积神经网络及其扩展网络。例如，Cha 等[13]及Dorafshan 等[14]利用卷积神经网络识别了混凝土的裂纹损伤，Liu 和Zhang[15]利用卷积神经网络识别了结构钢的超低周疲劳损伤裂纹，Reddy 等[16]利用卷积神经网络识别了风机叶片的裂纹损伤，Yao 等[17]利用卷积神经网络识别了船体结构板的腐蚀损伤，Ren 等[18]利用全卷积网络识别了混凝土中裂纹损伤。

基于振动响应信号处理的方法利用深度神经网络从振动响应中提取损伤特征，进而建立振动响应与结构健康状态的映射关系，目前研究中最常采用的都是卷积神经网络或自编码器。在这类方法中，主要研究集中在两个方面：一类为旋转机械的故障诊断；另一类为结构损伤检测。在旋转机械故障诊断研究中，Guo 等[19]提出了基于分层自适应深度卷积神经网络的轴承故障诊断方法，并采用轴承故障诊断实验验证了方法的有效性；Jing 等[20]提出了基于一维卷积神经网络的故障诊断方法，并利用PHM2019 变速箱数据以及行星齿轮箱数据验证了方法的有效性；Chang 等[21]提出了基于并行卷积神经网络的故障诊断方法，并采用涡轮机齿轮的故障诊断实验验证了方法的有效性；Chen 等[22]提出了基于卷积循环神经网络的故障诊断方法，并采用涡轮机齿轮的故障诊断实验验证了方法的有效性。在结构损伤检测研究中，Lin 等[23]提出了利用多个测点加速度响应作为深度卷积神经网络输入的损伤定位方法，并利用仿真简支梁的损伤检测示例验证了方法的有效性；Pathirage 等[24]以结构固有频率及模态振型为输入提出了基于堆栈自编码器的深度学习框架，建立了包含特征降维及关系学习两个步骤的结构损伤检测方法，并通过钢框架模型单位置及多位置损伤检测的仿真算例及实验研究验证了方法的有效性，之后他们利用堆栈稀疏自编码器来改善特征提取过程的抗噪性[25]，仿真及实验结果表明采用稀疏自编码器在存在测量噪声及模型不确定性的情况下可以显著提升检测精度；Liu 等[26]利用过桥车辆上测试的振动加速度信号及相关特征降维技术(主成分分析、等度量映射、拉普拉斯特征映射、堆栈自编码器)获取结构损伤特征，建立了用于桥梁损伤检测的数据驱动方法，通过损伤检测模型实验验证了方法的有效性，结果表明采用堆栈自编码器的检测效果最佳。

上述研究现状可以看出，不管是基于图像识别的表面损伤检测还是基于振动信号处理的各类型损伤检测，其基本原理都是利用深度神经网络强大的特征提取功能，建立可获取的损伤图像或振动响应与结构健康状态之间的映射关系。

笔者前期在基于振动信号处理的结构损伤检测研究中，以振动时域响应相关性分析为理论基础提出了一种称为内积向量(inner product vector，IPV)的损伤指标及对应的损伤检测方法[1]，通过框架结构的刚度下降损伤、蜂窝夹层复合材料梁的脱粘损伤、航空壁板的螺栓松动损伤等实验验证了方法的有效性[27]，研究了环境激励频带以及测试响应类型对检测方法的影响[28]，并结合数据融合技术提升了方法对微小损伤的检测精度[29]。研究表明，内积向量与结构的模态振型有关，可直接通过时域响应内积进行计算，且在其计算过程中可自动剔除相关测量噪声的影响。然而，这些前期的研究仅利用了结构时域响应的部分相关性分析数据来构建损伤指标，也没有采用大量的损伤指标给出具有统计意义的检测结果。考虑到深度学习中的卷积神经网络可以从大量数据中提取深层次的特征信息，并充分利用结构各个测点时域响应的相关性分析数据，本文将一维的内积向量扩展到了二维的内积矩阵，进而结合深度学习中常用的二维卷积神经网络，提出基于内积矩阵及二维卷积神经网络的结构健康监测方法，并通过典型航空加筋壁板螺栓松动的监测实验验证方法的可行性及有效性。

1 理论基础

本文以振动时域响应的相关性分析为基础，获取表征结构健康状态的原始特征信息，即内积矩阵，进而结合二维卷积神经网络的深层次特征提取功能，建立相应的结构健康监测方法。因此，这里首先介绍内积矩阵与二维卷积神经网络的基本概念与理论。

1.1 内积矩阵

假设可获得结构n个测点的时域响应x1(t),x2(t),···,xn(t)，取其中测点l的响应xl(t)为参考响应，内积向量为：

式中，Rkl(0)表示响应xk(t) (k=1,2,···,n)与响应xl(t)的互相关函数在时间延迟τ=0时的值，根据互相关函数的定义可知：

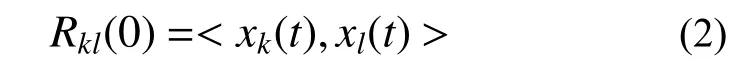
式中：＜,＞表示内积运算符。研究表明，在带通白噪声激励下内积向量是结构各阶模态振型的加权叠加，且各阶模态的加权系数与结构的模态参数有关[1,27-28]。对于一般的环境激励谱，可视为若干个不同频带范围的带通白噪声的组合谱，根据线性系统的叠加原理可知，在环境激励下内积向量仍是结构各阶模态振型的加权叠加，同时各阶模态的加权系数也与结构的模态参数有关。通常，结构物理参数的变化(例如结构损伤导致的局部刚度下降)会体现在相关模态振型的突变上，因此内积向量也会因结构局部损伤而发生突变，即可以利用内积向量作为结构损伤指标来进行结构健康监测。

可以看出，内积向量是一个典型的一维向量，且只包含了结构各测点时域响应的部分内积计算数据，而深度学习中常用的二维卷积神经网络的输入是一个二维矩阵，为了采用内积向量作为二维卷积神经网络的输入，并充分利用结构各测点时域响应的所有内积计算数据，可将内积向量扩展到内积矩阵。从内积向量的定义式可以看出，内积向量仅采用某一个测点l的响应xl(t)作为参考响应来与其他测点响应进行内积运算，若参考测点l的取值也分别设为各个测点，即l=1,2,···,n，则可获得内积矩阵：

结合内积向量的定义式，从内积矩阵的定义式可以看出，内积矩阵其实就是将参考响应测点分别设置为不同测点的多个内积向量依次排列组成的矩阵，因此内积矩阵也可以作为结构特征参数来进行结构健康监测。

1.2 二维卷积神经网络

二维卷积神经网络是深度学习中最常用的一种卷积神经网络，可以从二维图像中提取数据特征，其网络结构主要包括用于提取数据特征的卷积层(convolution layer)、避免训练过程梯度消失问题的批归一化层(batch normalization layer)、对数据进行降采样的池化层(pooling layer)、用于过渡的拉直层(flatten layer)、用于整合分类信息的全连接层(fully connected layer)以及用于网络输出的分类层(classification layer)等[13]。

在建立神经网络结构之后，需选取一个合适的损失函数(loss function)来训练网络，损失函数是用于评估模型预测值与真实值不一致程度的函数，对于不同的问题应选择不同的损失函数。结构健康监测往往可以抽象为分类问题，而针对分类问题，目前最常用的损失函数为交叉熵，其定义如下[21,23]：

式中：m为样本数量；k为分类的类别数量；p(xi j)是样本xi为第j类的真实概率；q(θ,xi j)为模型参数θ时将样本xi预测为第j类的概率。

2 方法原理

二维卷积神经网络通常用于处理图片信息，将图片每一个像素点的颜色信息作为特征，针对每一个图片构建一个数值矩阵，并以数值矩阵作为深度神经网络的输入。考虑到表征结构健康状态特征的内积矩阵也是数值矩阵，且与二维图片像素颜色信息构成的数据矩阵有着相同的形式，则可将内积矩阵作为二维卷积神经网络的输入来构建深度神经网络，以实现基于内积矩阵及卷积神经网络的结构健康监测。

基于深度学习的结构健康监测方法与传统的基于机器学习的结构健康监测方法类似，通常均包含2 个关键的步骤，即标签数据库的构建以及网络模型的设计。标签数据库是指用于训练、验证、测试模型的输入输出数据，通常由一组特征数据及其对应的结构状态标签构成。网络模型是指用于描述输入-输出关系的复杂非线性函数，在结构健康监测中，网络的输入为可测量的结构特征参数，网络的输出为结构健康状态标签。

结合作者前期研究以及二维卷积神经网络对输入数据的要求，本文以内积矩阵为网络输入数据。考虑到深度学习神经网络需要大量的带标签数据来训练模型，本文利用结构上多个测点的时域响应，并通过数据分组来构建标签数据库，具体实施过程如图1 所示。将结构各个测点的时域振动响应信号分割为若干个数据子集，每个数据子集均包含了各个响应测点在同一时间段的振动响应信号；利用每一个数据子集内的所有响应信号，按照式(3)计算内积矩阵，即可获得该数据子集对应的内积矩阵；针对若干个数据子集，可以获得若干个内积矩阵，这些内积矩阵就构成了当前结构健康状态下的标签数据库。

图1 结构健康监测标签数据库的构建Fig.1 Construction of the labelled database for structural health monitoring

根据图像识别研究中二维卷积神经网络的基本结构，图2 给出了本文采用的二维卷积神经网络结构示意图。输入层之后连接若干个卷积层，以逐层提取输入数据中所包含的结构健康特征信息；卷积层之后连接一个批归一化层及一个池化层，以提升网络训练效率并防止过拟合；池化层之后连接一个拉直层，以实现二维数据向一维数据的转变，用于后续的分类问题；拉直层之后连接若干个全连接层，以逐步整合前述层中具有类别区分性的局部信息；最后为分类层，以获得各个分类的概率，即给出结构的健康状态。

图2 深度卷积神经网络结构示意图Fig.2 Schematic diagram of the deep convolutional neural network architecture

本文方法的具体流程如图3 所示，即：利用图1 所示的方法，针对每一种结构健康状态，构建其内积矩阵集及其对应的健康状态标签集，获得样本数据库，并从中随机筛选出训练集、验证集以及测试集，按照图2 所示的方法设计深度卷积神经网络模型，然后，利用训练集及验证集进行模型训练，最终通过测试集验证模型的识别准确率。

图3 本文方法的流程框架Fig.3 Framework of the proposed methodology

3 实验验证

加筋壁板是航空领域中常用的一种结构形式，传统的加筋壁板一般采用螺栓或铆钉等紧固件将型材连接在壁板上，以提升壁板结构的承载能力，而紧固件松动是导致壁板承载能力下降甚至引发安全事故的隐患，本节将采用加筋壁板结构的紧固件松动监测来验证本文方法在航空结构健康监测中的可行性及有效性。

实验采用常见的四边固支加筋壁板，如图4所示，加筋壁板由1 块450 mm×350 mm×2 mm 的铝板以及3 根长度340 mm、截面宽度25 mm、壁厚2 mm 的等边角铝组成，每根角铝与铝板均用11 个M5 螺栓连接，加筋壁板四边由宽度为50 mm、厚度为20 mm、长度为450 mm 或350 mm 的8 块钢制夹板加持，以模拟四边固支边界条件。

图4 加筋壁板示意图Fig.4 Schematic diagram of the stiffened panel

为模拟航空结构所受的激励形式，本文采用某飞机振动环境谱作为激励，并采用加速度响应来构建内积矩阵，实验布置及现场照片如图5 所示。在m+p VibControl 振动控制系统中设置振动环境谱，并驱动东菱ET-50 振动台来激励四边固支壁板，最后利用Dewesoft SIRIUS 数据采集系统采集布置在壁板上的15 个PCB Piezoelectrics 333B30加速度传感器记录的加速度响应。实验中分别模拟了7 种结构状态，包括完好状态(即所有螺栓都完全紧固)以及分别松开编号为1、10、14、19、28、33 六个螺栓的6 种损伤状态。针对每一种结构状态，采用20 kHz 的采样频率进行加速度信号的采集，采集信号时长为50 s，即数据采样点数为106个。

图5 加筋壁板振动环境实验Fig.5 Vibration tests of the stiffened panel

3.1 标签数据库容量对识别结果的影响

在标签数据库的构建中，选取各加速度测点同一时间段的512 个采样点组成一个数据子集，来计算一个内积矩阵。标签数据库容量对深度学习方法一般有着显著的影响，为了研究标签数据库容量(即每一种结构健康状态所包含的内积矩阵个数)对监测方法的影响，分别从每一种结构健康状态的总数据库中按顺序选取包含64 个、128 个、256 个、512 个及1024 个内积矩阵的标签数据库来验证方法，则标签数据库的总容量(即模拟的7 种结构健康状态下的内积矩阵个数)分别为64×7、128×7、256×7、512×7 及1024×7，简称为数据库1～数据库5。考虑到内积矩阵是采用环境激励下的随机响应计算而得，总数据库中的内积矩阵相当于是随机生成的，因此这里构建的各个数据库中的样本数据也具有随机性。

考虑到本文研究用于输入的数据维数较小(15×15)且识别的结构健康状态数目不多(7 种)，结合图2 所示的深度卷积神经网络结构示意图，本文仅采用2 层卷积层及1 层全连接层，具体网络结构如表1 所列。在神经网络训练及方法验证过程中，针对研究的六种不同容量的标签数据库，训练集、验证集及测试集所采用的数据量均为8∶1∶1。

表1 采用的网络结构Table 1 The utilized network architecture

图6～图10 分别给出了利用数据库1～数据库5的网络训练过程的损失函数与识别准确率的变化曲线。从图中可以明显看出，随着数据库容量增大，训练收敛速度加快、损失函数数值减小、识别准确率提高，且训练集与验证集的差异越来越小。

图6 网络训练过程(数据库1)Fig.6 Training process of network (Database 1)

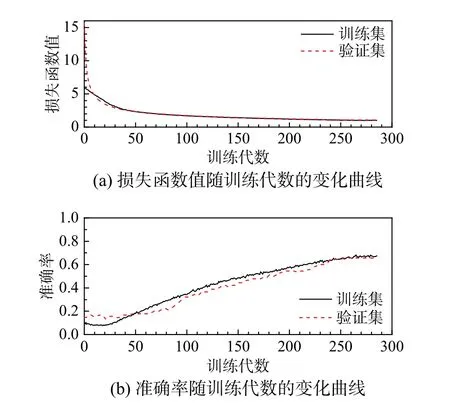
图7 网络训练过程(数据库2)Fig.7 Training process of network (Database 2)

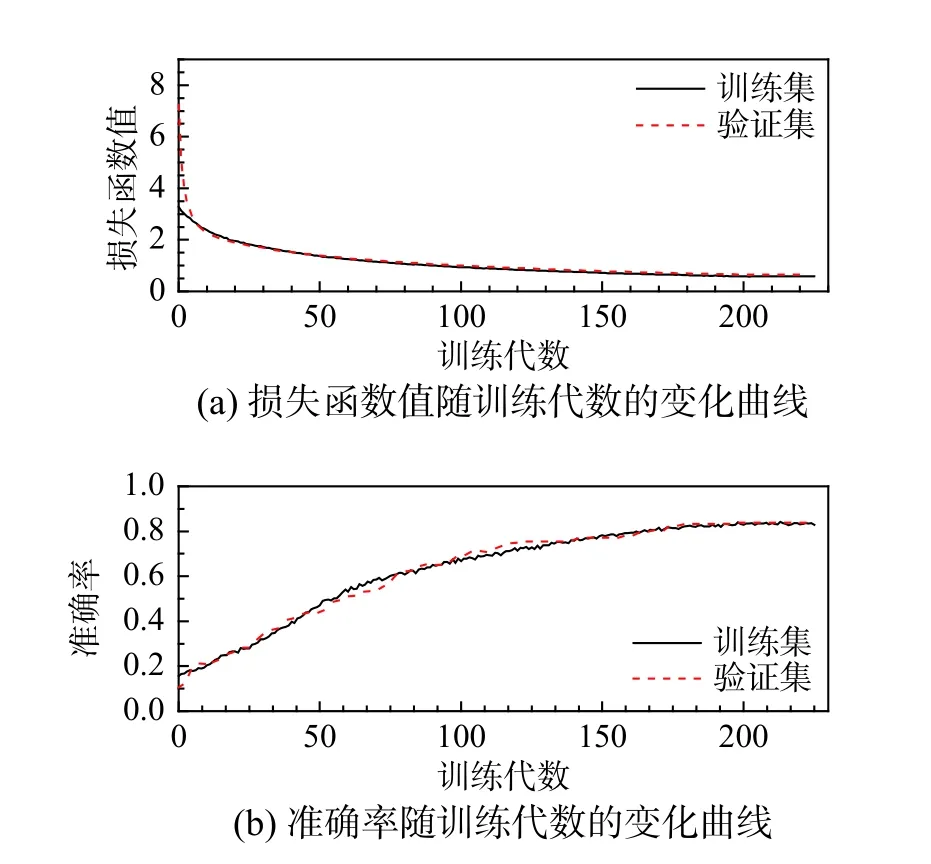
图8 网络训练过程(数据库3)Fig.8 Training process of network (Database 3)

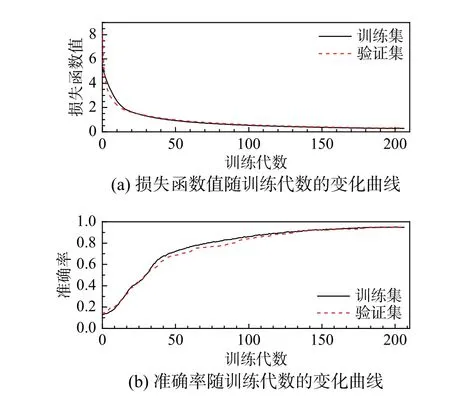
图9 网络训练过程(数据库4)Fig.9 Training process of network (Database 4)

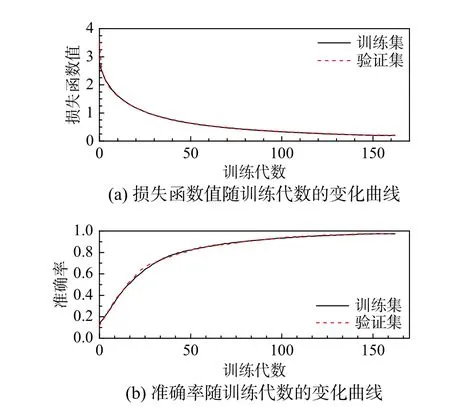
图10 网络训练过程(数据库5)Fig.10 Training process of network (Database 5)

为了进一步说明网络在测试集上的识别准确率，表2 列出了分别利用数据库1～数据库5 进行网络训练的最终损失函数值及识别准确率。可以看出，当数据容量很小时，由于样本数量不足，识别准确率很低，而当每一种结构健康状态所包含的内积矩阵个数为1024 时，网络在训练集、验证集以及测试集上的识别准确率均大于97%，这表明当数据库容量足够时，本文方法具有很高的识别准确率。上述图6～图10 以及表2 出现的规律表明，样本容量较大时以内积矩阵作为网络输入可准确识别螺栓松动位置，这是因为内积矩阵的特征变化：一方面是由螺栓松动引起；另一方面是由相关测试噪声引起。根据一般测试噪声具有的随机特性，在神经网络训练过程中通常可通过增加样本数量来减缓测试噪声的影响，因此随着样本容量的增加，网络的识别准确率显著增加。

表2 不同数据容量下网络的损失函数值及识别准确率Table 2 The loss value and accuracy for different datasets

为了进一步对比不同数据容量下训练的模型的识别准确率，针对每一种健康状态，分别选取100 个内积矩阵(不包含在上述数据库中)，组成用于验证模型准确率的固定测试集(即共包含100×7个内积矩阵)，表2 的最后一行列出了各个网络在固定测试集上的识别准确率。可以看出，固定测试集的识别准确率与训练集、验证集以及测试集上的识别准确率并无显著差异。

3.2 测点数量对识别结果的影响

在结构健康监测中，通常难以获得很多测点的测试数据，本节将研究测点数量对网络识别结果的影响。考虑到15 个测点情况下，标签数据库容量为1024 个时识别准确率较高，本节后续的研究中的数据容量均为1024 个。针对图5(a)中的测点布置，分别采用8 个测点、4 个测点的加速度响应进行螺栓松动识别。按照测点尽可能均布的原则，针对8 个测点，选取(1)、(3)、(5)、(7)、(9)、(11)、(13)、(15)号测点；针对4 个测点，选取(3)、(7)、(9)、(13)号测点。

采用同样的网络结构以及标签数据库容量进行网络训练，结果发现：当测点数量为8 时，网络识别准确率下降到90%以下，当测点数量为4 时，网络识别准确率下降到80%以下。分析出现这一情况的原因，主要是由于测点数量降低，在其它参数不变的情况下，导致包含结构健康信息的原始数据量下降，网络难以从不足的信息中提取结构健康特征。在测点数量不足的情况下，通常可以从单个测点获取更多的数据来提升特征信息量，基于此，本节将上节计算内积矩阵所采用的512 个加速度采样点逐步增加到1024 个、2048 个、4096 个、8192 个，以研究测点数量对网络识别准确率的影响，表3～表5 分别给出了15 个、8 个以及4 个测点数量下网络的最终损失函数值及识别准确率。

表3 15 个测点下网络的损失函数值及识别准确率Table 3 The loss value and accuracy of the network by 15 measurement points

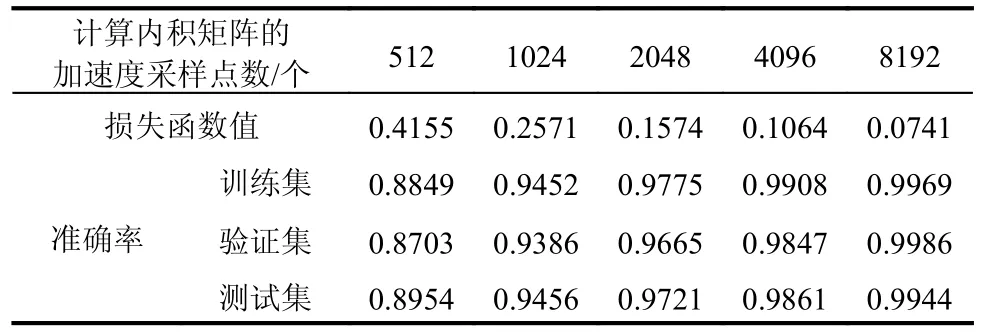
表4 8 个测点下网络的损失函数值及识别准确率Table 4 The loss value and accuracy of the network by 8 measurement points

表5 4 个测点下网络的损失函数值及识别准确率Table 5 The loss value and accuracy of the network by 4 measurement points

当计算内积矩阵的加速度采样点数从512 个增加到8192 个时，从表3～表5 可以看出：当采用15 个测点时，准确率略有提高(从97%增加到99%)；当采用8 个测点时，准确率有明显提高(从小于90%增加到99%)；当采用4 个测点时，准确率显著提高(从小于80%增加到98%)。为了说明加速度采样点个数以及测点数量对计算耗时的影响，表6 给出了表3～表5 所有情况的计算耗时(含构建数据库耗时及模型训练耗时2 部分)，可以看出：1)构建数据库的耗时随着加速度采样点或是测点数量的增加而增加，这是因为加速度采样点越多、测点数量越多，进行内积运算的数据量越大，因而耗时越多；2)模型训练的耗时随着加速度采样点或是测点数量的增加而减小，这是因为加速度采样点越多、测点数量越多，提取的结构特征信息越显著，网络训练越容易收敛，因而耗时越少；3)综合构建数据库及模型训练两部分耗时，单纯增加加速度响应点个数或是减少测点数量对整个计算耗时并没有显著影响。上述分析结果表明，本文方法即便是在测点数量较少的情况下，合理增加计算内积矩阵的加速度采样点个数可显著提升网络的识别准确率，且整个计算耗时并没有显著变化。

表6 不同情况下的计算耗时Table 6 Computational time consuming for different cases

为了进一步说明测点位置对监测结果的影响，针对4 个测点的情况，选取了远离螺栓松动位置的(2)、(8)、(10)、(11)号测点进行研究，表7给出了这种情况下网络的最终损失函数值及识别准确率。对比表7 和表5 可以看出，当测点数量不变仅改变测点位置时(且测点位置远离螺栓松动位置)，各种状态下网络的识别准确率并无显著差异，这说明本文方法受传感器位置的影响较小。

表7 采用远离螺栓松动位置的4 个测点时网络的损失函数值及识别准确率Table 7 The loss value and accuracy of the network by 4 measurement points located far from the loosed bolt

上述研究表明，利用结构上少量测点在环境激励下的时域加速度响应信号，并选取足够的加速度采样点来计算内积矩阵，进而以内积矩阵作为输入来构建深度卷积神经网络，可以有效地识别典型航空加筋壁板的螺栓松动位置。

4 结论

通过将各个响应测点分别设置为参考点，构建了多个内积向量并将其组成矩阵，提出了内积矩阵的概念。然后，根据内积矩阵的定义以及深度学习神经网络训练对数据库的需求，针对完整的测试数据引入了数据分组策略，获得了多个数据子集，通过在每一个数据子集中进行内积矩阵计算，建立了包含内积矩阵与结构健康状态一一对应的标签数据库构建方法。进而以内积矩阵为输入、结构健康状态为输出，构建了包含卷积层、批归一化层、池化层、拉直层、全连接层以及分类层的深度卷积神经网络结构，提出了基于内积矩阵及深度学习的结构健康监测方法。

利用典型航空加筋壁板的螺栓松动监测实验验证了方法的可行性及有效性，结果表明：1)随着标签数据库容量的增大，网络训练收敛速度加快、损失函数数值减小、识别准确率提高；2)当每一种结构健康状态所包含的内积矩阵个数足够、且计算内积矩阵的加速度采样点个数充足时，即便是仅有少量测点的加速度响应数据，网络在训练集、验证集以及测试集上的识别准确率均可达到98%以上。