相同条件下一类不等式问题的探究

江苏省仪征中学 (211400) 李军焰

在一些不等式问题所给出的条件中，“已知正数a，b，c满足abc=a+b+c+2”出现的频率较高.本文首先给出“abc=a+b+c+2”的几个等价形式，然后探究以“abc=a+b+c+2”或它的等价形式为条件的一些不等式问题，最后探究“abc=a+b+c+2”的几何背景，仅供参考.

1.abc=a+b+c+2的等价形式

证明：由abc=a+b+c+2，两边同除以abc，移项即得(1).

2.abc=a+b+c+2或其等价形式为条件的不等式问题

以“abc=a+b+c+2”或其等价形式作为条件，可以得到许多有趣的不等式.

例1 已知正数a，b，c满足abc=a+b+c+2，求证：abc≥8.

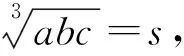
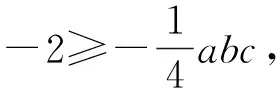
例3 已知正数a，b，c满足abc=a+b+c+2，求证：ab+bc+ca≥2(a+b+c). (2005年哈萨克斯坦数学奥林匹克竞赛题)

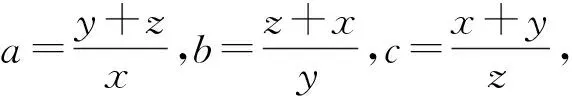
下面来证明(1)式成立.

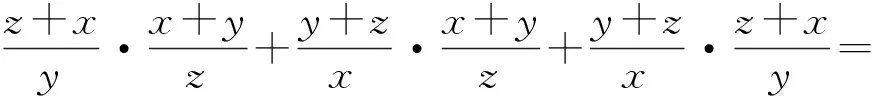
例4 已知正数a，b，c满足abc=a+b+c+2，求证：a2+b2+c2+2(a+b+c)≥2(ab+bc+ac).

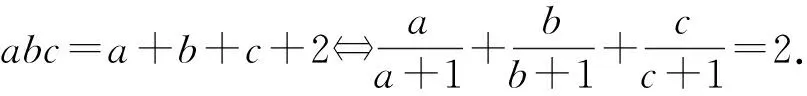
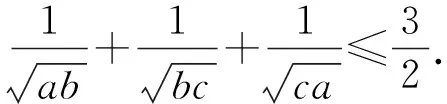
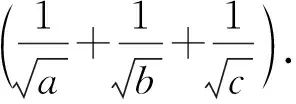
证法1：由例1可知abc≥8.

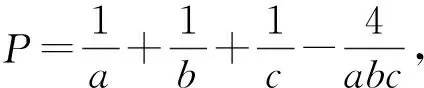
点评：证法1将条件abc=a+b+c+2变形为2=abc-a-b-c进行“常数代换”，两次运用3元均值不等式后换元将不等式等价转化，借助二次函数的最值完成不等式证明的.

下面来证明(1)式成立.

点评：证法2首先将所证不等式等价转换，然后实施代换，应用舒尔不等式和2元均值不等式，巧妙地进行了化简证明.

3.abc=a+b+c+2的几何背景

如图1，在△ABC及其内部的任意一点G，直线AG，BG，CG交三角形的对边于D，E，F，记△ABC，△BGC，△AGC，△AGB，的面积分别为S，S1，S2，S3，则S=S1+S2+S3.

图1