两个不等式的简证

山东省邹平双语学校 (256200) 姜坤崇

山东省邹平市临池镇古城小学 (256220) 孟凡慎

文[1]以鲜明的观点阐述了化分式不等式为整式不等式是证明分式不等式的一条重要途径，并举出了若干例子加以说明.同时，文中绝大部分例子证明得都很简洁，但其中的两例用化为整式不等式的方法来处理给人以繁冗之感，本文给出这两例的几个简证.

例1 (文[1]例7)已知a,b,c>0,abc=1,求证：

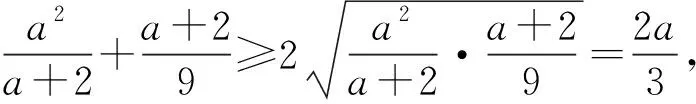
评注：以上简证使用的方法是配凑项(也称添加项)法，它是证明分式不等式的一种常用技巧.

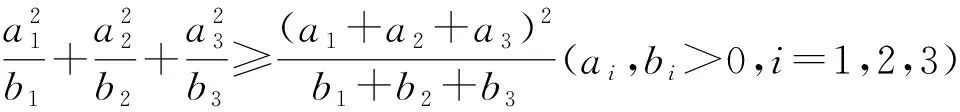
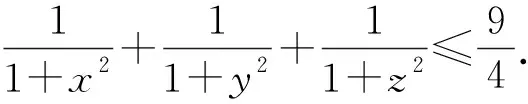
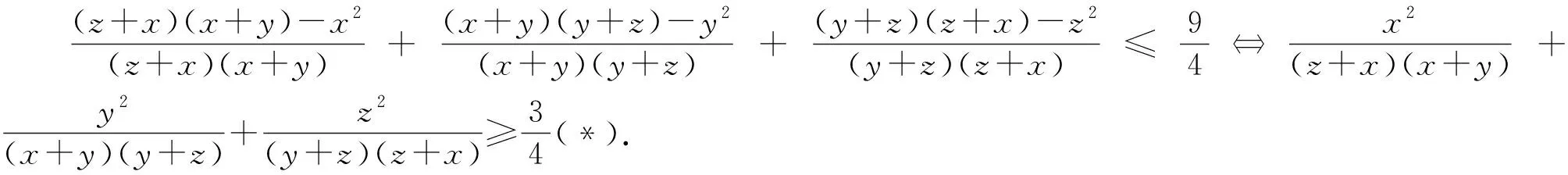
将不等式(*)化为整式不等式得x2y+xy2+y2z+yz2+z2x+zx2≥6xyz⟺x(y-z)2+y(z-x)2+z(x-y)2≥0,由于以上最后一个不等式显然成立，所以所证不等式成立.

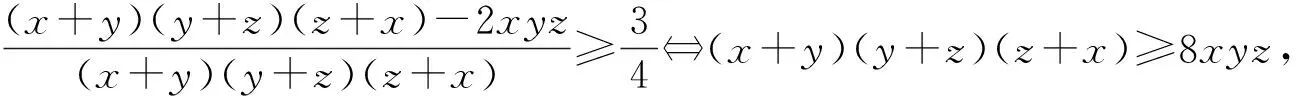
评注：以上简证将所证不等式转化为不等式(*)来证明，使用的方法技巧是齐次化和等价反向转化，这两种方法也是证明不等式的常用方法.