基于深度强化学习的多域联合干扰规避

潘筱茜 张 姣 刘 琰 王 杉 陈海涛 赵海涛 魏急波

（1.国防科技大学电子科学学院，湖南长沙 410073；2.中国人民解放军91428部队，浙江宁波 315456）

1 引言

随着信息化战争时代的到来，敌我双方围绕通信干扰与抗干扰的电子战已经成为信息化战争的重要组成部分。为应对敌方恶意生成的电磁干扰，当前通信抗干扰主要目的是依据通信任务的需求与战场干扰环境动态变化，在电磁和网络空间形成电磁频谱安全非对称制衡能力。未来信息化战场的主要特征就是网络中心化、智能化以及多样化。通信干扰设备不断发展进步，其具备的感知、分析、学习能力，使其可以轻易干扰正在进行的通信传输。面对智能化通信干扰时，传统的抗干扰通信体制已经很难取得理想的效果。

针对无线通信系统中存在的电磁干扰问题，现有工作分别基于时、频、空、功率等通信资源构建抗干扰优化模型，并提出优化算法求解最优抗干扰策略。文献［1-3］采用了博弈论方法建模，很好地模拟了合法用户与干扰者之间的交互，通过求解纳什均衡获得最优通信策略。启发式优化算法［4］也广泛用于多域参数的决策，文献［5］研究了人工蜂群算法（ABC，Artificial Bee Colony Algorithm）在认知抗干扰系统中智能决策中的应用。上述优化算法依赖于数学模型，然而环境的动态特性往往会造成实际系统与理论模型的不匹配，无线通信需求的增长也使各种优化算法开销增大。

近年来，人工智能和机器学习研究取得重大进展，尤其是在计算机视觉、语言等领域，主要包括深度学习（DL，Deep Learning）［6］、深度强化学习（DRL，Deep Reinforcement Learning）［7］、联邦学习（FL，Federated Learning）［8］。这些进展吸引研究者将机器学习技术与智能抗干扰相结合，机器学习算法不依赖于模型，直接通过智能体与环境之间的交互捕获到环境动态变化的规律，从而学习到最佳决策。文献［9-11］总结了近年来基于机器学习的抗干扰技术，包括博弈论学习、强化学习和深度学习以及联邦学习在无线通信领域的应用。文献［12］采用单智能体Q 学习算法在宽带自主认知无线电中进行通信抗干扰，考虑干扰器在目标频谱范围内进行扫频干扰的场景，强化学习算法目标是选择连续空闲的频带，实现尽可能长时间的不间断传输，该算法证明了学习到的抗干扰选择策略的优良性能，但由于其不允许在被干扰之前通过预测干扰器的行为有效改变子频带，模型过于简单不能很好的适用于实际对抗场景。文献［13］提出了一种基于深度强化学习的抗干扰算法，该算法可以同时对通信频率和功率进行决策，但是该算法并没有考虑信道切换的代价。受DRL 的启发，文献［14］提出了一种基于深度强化学习的抗干扰方法，将频谱瀑布直接输入到卷积神经网络（CNN，Convolutional Neural Network）中，估计通信动作的Q 值，解决了状态数无限的复杂交互式决策问题。

综上，针对无线通信系统中存在的恶意电磁干扰问题，现有智能抗干扰技术主要考虑从时间、频率以及功率域等多维度设计抗干扰策略，但仍然还存在以下问题：（1）现有的抗干扰技术主要考虑从时、频、空或功率域单维度或者两两联合等角度来规避干扰，虽然所设计的抗干扰算法收敛较快，但是系统性能没有达到最优；（2）现有强化学习算法在面对较大动作空间时训练难以收敛、收敛速度慢、算法不稳定。本文针对上述问题，采用深度强化学习算法中基于剪裁的近端策略优化算法（PPOClip）［15］，从信道切换、功率控制、调制编码方式三个维度进行联合干扰规避决策，并将PPO-Clip 算法与Q 学习算法进行对比分析，验证了PPO-Clip 算法在联合干扰规避问题中收敛速度快，系统性能好。

2 模型

2.1 问题分析

无线通信环境中的一对通信节点对，受到来自外来恶意干扰节点的干扰，假设两个通信节点皆为智能节点，通过调整通信参数规避干扰。系统模型如图1所示。

图1 系统模型Fig.1 System model

假设该系统中收发双方的通信功率、调制方式、码率和传输信道可调节，发射功率集合为Pu={pu，1，pu，2，pu，3，…，pu，L}，调制方式集合为Mod={m1，m2，m3，…，}，编码速率集合为Cod={c1，c2，c3，…，}，第k个时隙所使用的发射功率为pu，k（pu，k∈Pu），第k个时隙的传输速率由调制编码方式决定：vk=cklog2mk（mk∈Mod，ck∈Cod，vk∈{v1，v2，v3，…，vN}，N=N1×N2）。干扰功率集合设为：Pj={pj，1，pj，2，pj，3，…，pj，Q}，第k个时隙干扰功率为pj，k，pj，k∈Pj，噪声功率为σ2。假设智能节点能完全感知当前的干扰状态，且认为一个时隙内干扰不发生变化。收发双方需要根据当前时刻的状态选择合适的信道、发射功率和通信波形实现正常通信，考虑信道切换、改变发射功率以及调制方式和码率对系统整体性能的影响。信道切换代价，表示后一时隙选择的通信信道与当前时隙的通信信道不同时，由于通信链路的重建需要通信设备的稳定和重建时间，因此进行信道切换会带来系统性能损失；发射功率对系统性能影响表现在发射功率越大，通信系统的功耗也越大，对于通信设备的电源要求越高，并且不利于反侦察，因此产生的系统成本也越大；改变调制方式和码率同时传输速率也会改变，传输速率对系统性能的影响一方面表现在传输速率越快，系统性能越好，另一方面速率越快通信成功的阈值也越高。因此，在未知且动态变化的干扰环境中，需要衡量信道切换、发射功率以及传输速率的综合影响，选择最优策略来规避干扰，以最小的代价完成正常通信。

2.2 马尔可夫决策过程

强化学习背景下的MDP过程通常采用状态、动作、转移概率、折扣因子和奖励这五个元素描述，五个元素可以定义为一个五元组(S，A，P，γ，R)［16］。本文将点对点通信中未知干扰环境下发送机信道切换、功率控制和传输速率控制过程建模为一个MDP过程，在此模型中，状态空间和动作空间均是离散的。具体的MDP模型建模如下：

（1）状态空间

定义第k个时隙的状态为sk=(fu，k，fj，k，pu，k，pj，k，vk)，其中fu，k，fj，k∈{1，2，…，M}，分别表示当前时隙的通信信道以及当前时隙干扰所在的信道，M为系统可用的总信道数，pu.k∈Pu表示当前时隙的通信功率，pj，k∈Pj表示当前时隙的干扰功率，vk∈{v1，v2，v3，…，vN}表示当前时隙通信传输速率，所有可能的状态s合集记为状态空间S。

（2）动作空间

定义在第k个时隙用户采取的动作为ak=(fu，k+1，pu，k+1，vk+1)，其中fu，k+1∈{1，2，…，M}，pu，k+1∈Pu，vk+1∈{v1，v2，v3，…，vN}，表示第k+1 个时隙用户选择的通信信道、发射功率和传输速率，所有可能的动作a合集记为动作空间A，动作空间大小为M×L×N。

（3）状态转移概率

状态转移概率记为P：S×A×S→[0，1]，表示给定状态sk∈S下选择动作ak∈A并转移到下一状态sk+1∈S的概率，假设状态转移概率为确定值。

（4）折扣因子

折扣因子0 <γ≤1，表示未来收益对当前收益的重要程度。

（5）奖励函数

当用户在sk状态执行动作ak时，会获得相应的奖励值rk，奖励合集定义为R。这里定义第k个时隙的信干噪比（SINR，Signal to Interference plus Noise Ratio）为：

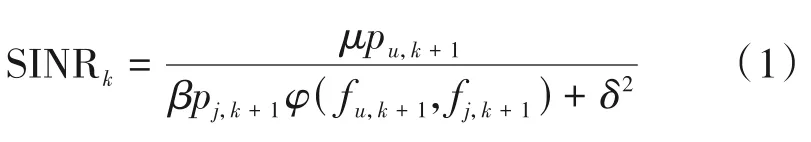
其中0 ≤β≤1，表示干扰功率在接收端的衰减因子，μ为信道增益。

即如果通信信道受到干扰，则φ(·)为1；否则为0。当SINR ≥Th时，表示当前通信成功；否则表示当前通信失败，其中Th表示根据实际应用所选择的最小SINR 门限值，门限值与当前传输速率相关，图2是信干噪比门限和传输速率对应关系示意图。

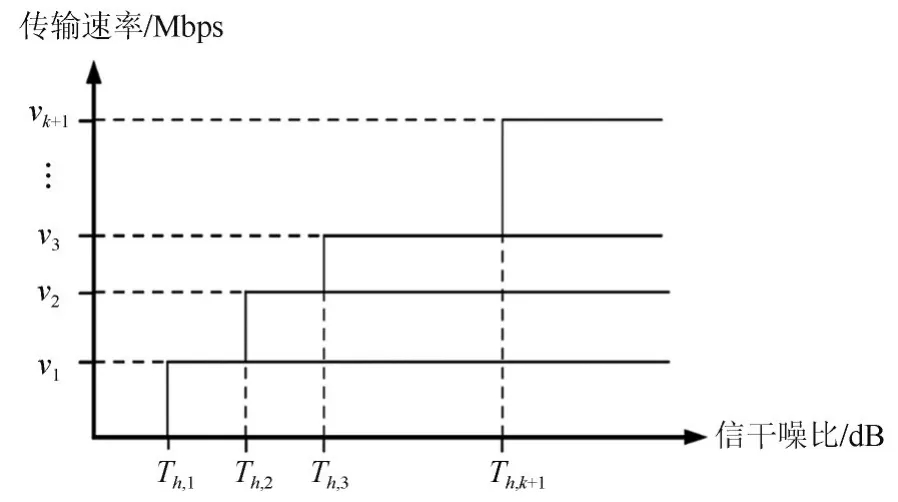
图2 传输速率和信干噪比门限关系Fig.2 Relationship with transmission rate and signal to interference plus noise ratio threshold

设信道切换代价为Ch，功率代价为pu，max表示最大发射功率，将相应的奖励值rk定义为：

在学习过程中，用户不断与环境交互，探索干扰的变化规律，从而获得最优的传输策略。在执行阶段，根据状态信息和学习到的策略快速执行。本文的系统目标是优化用户的传输策略π：S×A→[0，1]，使系统的折扣收益期望η(π)最大：

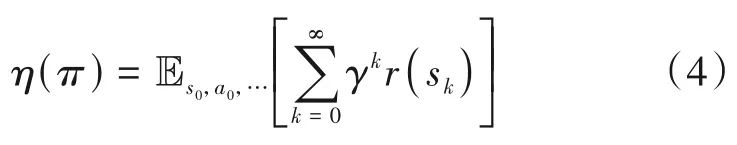
其中E[•]为期望。

3 算法

3.1 Q-Learning算法

强化学习算法中基于值函数网络采用状态-动作值函数来评价智能体在某一状态下选择某一动作的好坏：

Q-Learning 算法求解MDP 模型的主要思路是将状态和动作构建成一张二维Q 表，学习过程中利用这张二维表格存储Q 值，然后根据Q 值来选取能够获得最大收益的动作。Q 表中的元素即Q(s，a)，表示在某一时隙的s状态下（s∈S），采取动作a（a∈A）后能够得到的累计奖励值的期望。在第k个时隙的状态s下采取动作a，更新的Q函数为［17-18］

其中，sk，ak分别表示当前的动作和状态，α∈(0，1]表示学习率，γ∈(0，1]表示折扣因子，rk代表在sk状态执行动作ak时获得的奖励值。Qk(sk，ak)为当前的Q值，Qk+1(sk，ak)则表示更新后的Q值。maxaQk(sk+1，a)表示下一个状态所有Q值中的最大值。

在基于Q-Learning 的选择策略中，如果用户总是选择Q 值对应最大的动作，算法容易陷入局部最优，因此可以采用贪婪策略选择动作。在贪婪选择动作的过程中，产生一个[0，1]的随机数pr，如果该数小于ξ，则随机采取一个动作，否则选择Q 值最大对应的动作。贪婪策略定义如下：

ξ的值随着智能体对Q 表探索的逐渐完整而逐渐减小。

基于Q-Learning 的功率、信道传输速率选择策略具体步骤如算法1所示。

Q-Learning 算法需要搜索整个状态空间，由于系统模型中动作空间和状态空间数值较大，因此算法收敛速度慢。在实际无线通信场景中，很难预知干扰的动态变化情况。因此，本文进一步提出了一种基于深度强化学习的PPO-Clip算法。

3.2 PPO-Clip算法

（1）策略梯度

定义值函数Vπ，用于评价策略网络中智能体某一动作的好坏，定义优势函数Aπ：

策略梯度算法的优化目标是找到最优的神经网络参数θ∗使得关于轨迹的期望优势最大，目标函数构造如下：

策略梯度法的原理是计算出某一策略的梯度估计值，将这个估计值代入随机梯度上升算法，通过对目标函数的微分得到估计量，梯度估计量计算表达式如下：

其中πθ是一个随机策略是在一个时隙k上优势函数的估计，表示在抽样和优化之间交替的算法中，有限批样本的经验平均。最后对参数进行更新如下：

（2）演员-评论家算法

演员-评论家算法（Actor-Critic）框架融合了基于值函数估计与基于策略搜索的算法，集成二者的优点而广泛应用于深度强化学习算法中，是解决强化学习最常考虑的算法，算法框图如图3 所示。AC框架包含两个部分，Actor网络采用的是基于策略的策略梯度算法，通常使用时间差分误差TDerror来评价策略值：

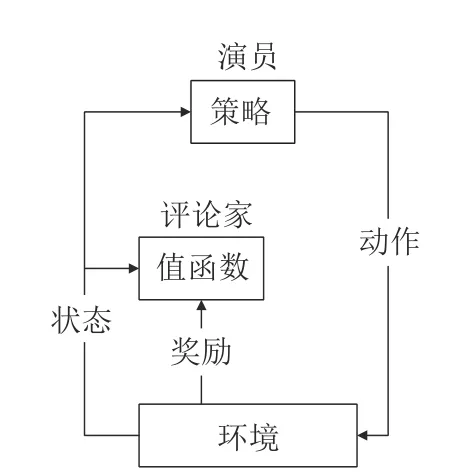
图3 演员-评论家算法框图Fig.3 Framework of Actor-Critic algorithm

此时损失函数可以表示为

Critic 网络采用的是基于值函数的Q-Learning算法损失函数表示为：

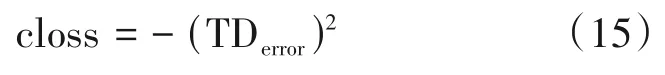
该算法解决了基于值函数求解方法的高偏差和基于策略求解方法的高方差问题，即设计一个智能体既能直接输出策略又能通过值函数评价当前策略的优劣。引用深度学习中的深度网络来拟合输出的值函数和策略，随着不断更新迭代，策略会越来越接近最优，值函数评价也会更加准确。

（3）PPO-Clip算法

本文采用一种基于目标剪裁的近端区域策略梯度算法（PPO-Clip）是演员-评论家算法的一种改进算法。进行策略网络的优化时，步长过小，则会导致训练速度过慢，且无法充分利用采样数据，造成训练的低效。但如果步长过大，策略网络容易进行过大程度的参数更新，反而造成策略变差，并且在较差的策略下进行采样，又会带来较差的采样数据，造成训练的崩溃。PPO-Clip 算法采用的目标函数可以在多回合训练中以小数量样本迭代更新，解决了策略梯度算法中步长难以确定和策略更新差异过大的问题。新策略可以使用从旧策略中采样出的样本来进行更新，设置优化目标为：

其中rk(θ)表示新旧策略的比值：

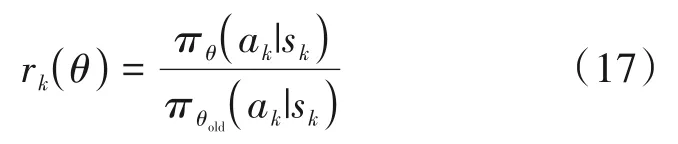
若新旧策略差异过大，则对优势函数进行剪裁：

剪裁函数：

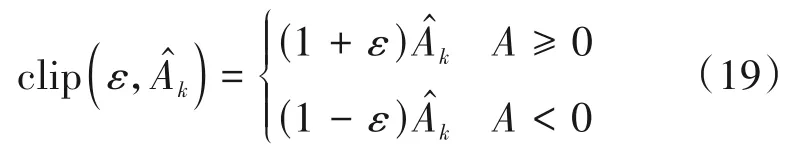
ε为超参数，表示剪裁比例，剪裁函数的作用是限制新旧策略之间的差异不要过大。

PPO-Clip算法具体框架如图4所示。

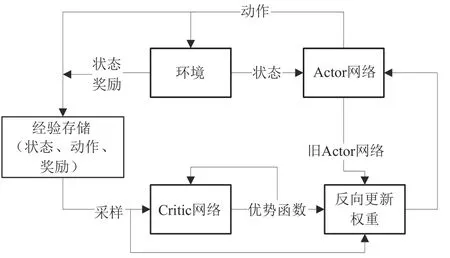
图4 PPO-Clip算法框架Fig.4 Framework of PPO-Clip algorithm

采用PPO-Clip 算法，复杂度高，但是算法收敛性能好，在实际规避干扰的过程中，能够实时进行决策而不受环境动态变化的影响，在应对复杂多变干扰时能展现出更好的适应性。

4 仿真分析

4.1 仿真参数设置

为了对系统性能进行评估，仿真过程中在每50个时隙内累积并统计一次奖励值。具体仿真参数如表1及表2所示。

表1 仿真参数Tab.1 Simulation parameters

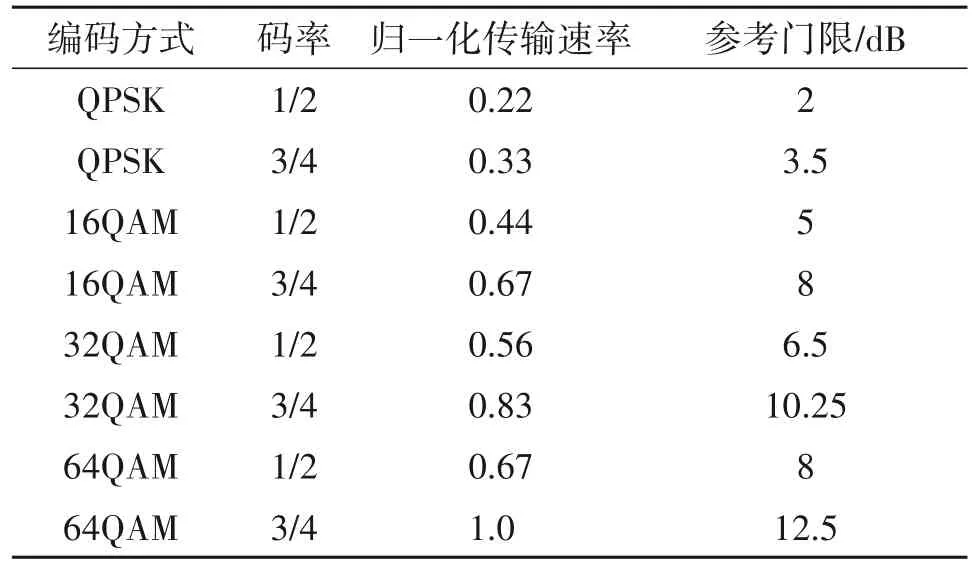
表2 归一化传输速率和参考门限Tab.2 Normalized transfer rate and reference threshold

为设置合适的PPO-Clip 算法学习率，对三种常用的学习率进行了仿真分析，具体的累积奖励曲线如图5所示。由图5可知，当学习率为0.01时，算法收敛慢，且收敛曲线出现较大波动，在300个epoch结束时，奖励收敛到20左右，可见在此情况下系统性能较低。当学习率为0.001时算法收敛速度有所提升，但是随着学习的进行到200个epoch之后，出现了奖励下降的过程。学习率为0.01和0.001时都出现了不同程度的奖励波动和下降，可能是由于学习率较大，容易受到输出误差或样本池中的异常数据的影响。当学习率为0.0001时，奖励曲线上升趋势明显，且奖励收敛到较大的数值，随着时隙增加系统性能稳定。因此后续仿真中均采用0.0001的学习率。

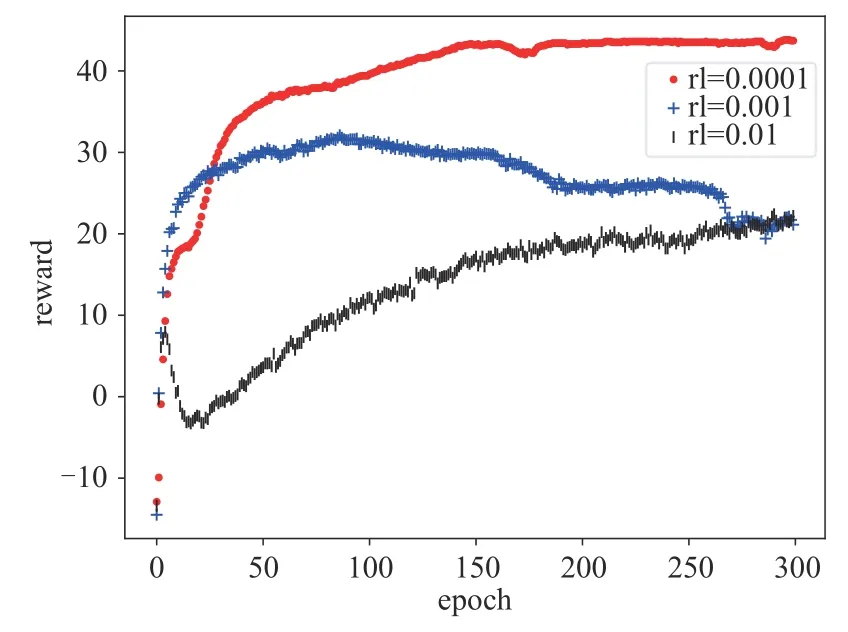
图5 不同的参数对PPO-Clip算法性能影响Fig.5 The effect of different parameters on the performance of PPO-Clip algorithm

4.2 PPO-Clip算法决策结果

利用图表详细展示了PPO-Clip 算法在扫频干扰下20个时隙的决策结果，决策结果主要包括信道切换、功率控制和调制编码选择。

如图6 所示，针对扫频干扰这种典型干扰场景进行了时隙信道切换GUI展示。设置6个频率不重叠的通信信道，图中纵坐标表示信道编号，横坐标代表时隙编号。红色代表当前时隙存在干扰的信道，颜色越深干扰功率越大，假设扫频干扰的周期为3，每个时隙存在2 个信道干扰，下图所展示的周期性干扰信道为（4，2；5，1；6，3）。蓝色代表当前时隙的通信信道，白色部分代表当前时隙的空闲信道。黄色表示当前时隙下干扰和通信存在于同一信道中，且通信成功（即SINR 值小于当前时隙门限值）。表3 对应图6 所示20 个时隙PPO-Clip 算法的干扰规避决策。由下图可知，在第2、11、17 和18 个时隙，虽然通信被干扰，但是通过调整功率和调制方式以及码率仍能实现成功通信。

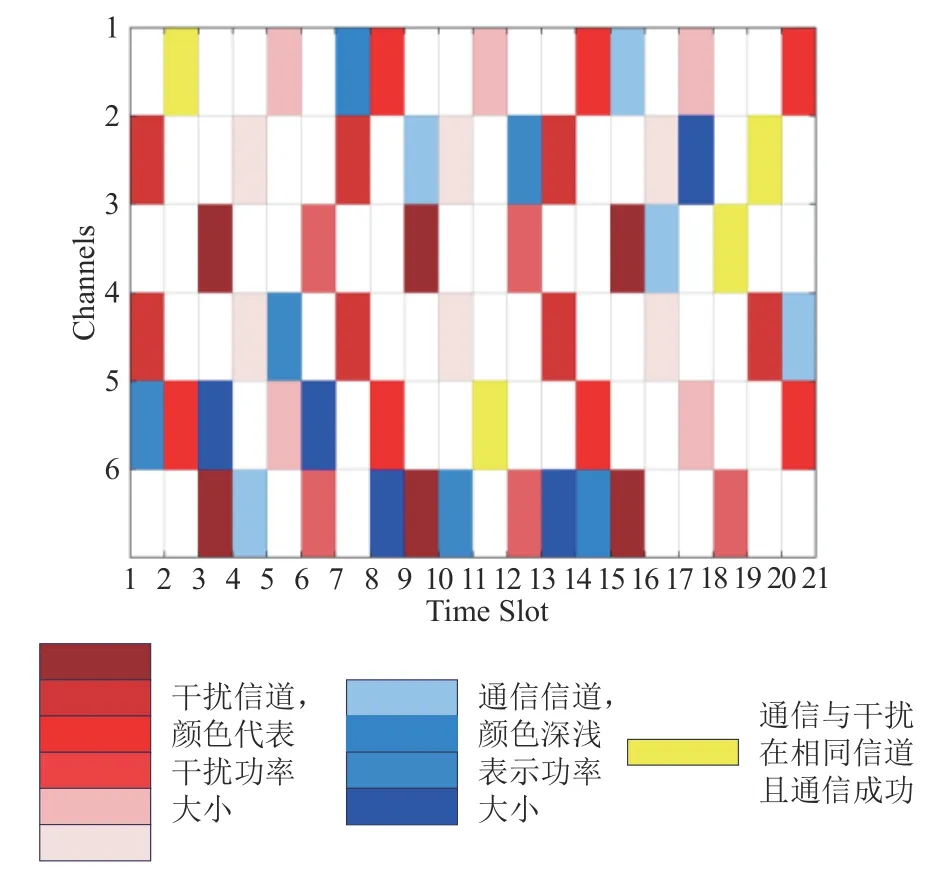
图6 扫频干扰环境下系统时频图Fig.6 System time-frequency plot in a sweep interference environment

表3 干扰规避决策结果示例Tab.3 Example of interference avoidance decision results

4.3 算法性能对比分析

为进一步验证所提PPO-Clip 算法的性能，在扫频干扰、随机扫频干扰和智能阻塞干扰这三种典型干扰场景下，将PPO-Clip 算法、Q-Learning 算法以及随机策略进行仿真分析对比。图7给出了三种典型干扰场景下的算法累积奖励曲线。

图7 不同干扰环境下累积奖励曲线Fig.7 The cumulative reward curve under different interference environments

（1）扫频干扰

设置干扰扫频周期为3，每个时隙存在两个干扰信道，干扰功率随机。如图7（a）所示。随机策略50 个时隙的累积奖励在-20 左右波动，且奖励不收敛。PPO-Clip 算法和Q-Learning 算法均优于随机策略。可以观察到PPO-Clip 比Q-Learning 收敛速度更快，Q-Learning 算法在150 个epoch 达到收敛，PPO-Clip 算法在第50 个epoch 达到收敛，说明在应对未知干扰时PPO-Clip 算法能够更快速的学习干扰规律并适应环境，采取最优策略使用户完成有效通信。在算法收敛后，PPO-Clip 算法的性能也要明显高于Q-Learning 性能。Q-Learning 累积奖励数值收敛在37 左右，PPO-Clip 累积奖励数值收敛在43 左右。由仿真结果可知，PPO-Clip 比QLearning 可以获得更快的收敛速度，且性能优于QLearning，但在奖励数值上差别不是很大。对于干扰规律固定的环境，PPO-Clip 收敛快，且奖励性能好，Q-Learning 收敛慢，但是奖励性能和PPO-Clip差距小。

（2）随机扫频干扰

随机扫频每个时隙干扰两个信道，从第一个时隙开始按随机顺序对6 个通信信道进行扫频干扰，三个时隙后遍历整个通信信道集合并切换扫频的顺序。如图7（b）所示，在随机扫频干扰场景下，由于随机扫频的随机性更强，PPO-Clip 算法收敛速度明显高于其他两种算法，并且在算法收敛后，PPOClip 累积奖励数值收敛在43.4 左右，明显高于其他两种算法。

（3）智能阻塞干扰

假设干扰机具有一定感知能力，能获取上一时隙的通信信道。每个时隙干扰机干扰两个信道，其中一个为上一时隙的通信信道，另一个在除上一时隙通信信道外的其他5 个信道内随机选择，干扰功率随机。如图7（c）所示，在智能阻塞干扰场景下，Q-Learning 算法和随机策略的性能进一步下降，而PPO-Clip 算法的性能却有所提升，这是由于PPOClip 算法，能够分析利用干扰信道规律做出更合理的决策。

由仿真结果可知，在三种典型干扰场景下，PPO-Clip 算法的性能均优于其他两种算法。在应对干扰规律相对简单的扫频干扰时，基于深度强化学习的PPO-Clip 算法与基于强化学习的Q-Learning算法的性能差距较小。在应对干扰规律复杂的随机扫频干扰、智能阻塞干扰时，PPO-Clip 算法性能明显优于Q-Learning 算法，体现出了深度强化学习的优势。

表4 至表6 分别了比较不同算法的学习速度、数据效率、时间复杂度以及通信成功率。算法的学习速度用达到特定奖励所花费的时间步长倒数表示，在本文仿真分析中，以奖励到达10 所花费的时间步长倒数表示；数据效率用训练智能体达到最佳性能所用数据量的倒数表示；时间复杂度用同样条件下平均进行一次决策所需要的时长表示；通信成功率指通信成功的时隙占总时隙数的百分比。通过表4 至表6 可以看出，PPO-Clip 算法仅在时间复杂度方面略逊于Q-Learning 算法，但是在学习速度、数据效率和通信成功率方面均超过Q-Learning 算法，特别是在随机扫频干扰和智能阻塞干扰这种复杂智能干扰场景下，表现出优秀的干扰规避性能。

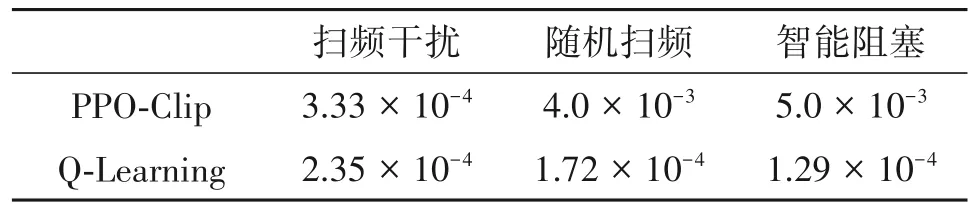
表4 不同算法的学习速度Tab.4 The speed of different algorithms

表5 不同算法的数据效率和时间复杂度Tab.5 The data efficiency and time complexity of different algorithms

表6 不同算法的通信成功率Tab.6 The communication success rate of different algorithms

5 结论

本文提出了一种基于深度强化学习的多域联合干扰规避方法。以最大化系统收益为目标，利用PPO-Clip 算法构建了干扰规避模型，能够有效提供结合发射功率控制、信道接入和调制编码适变的多域联合干扰规避决策。通过扫频干扰、随机扫频干扰和智能阻塞干扰三种典型干扰场景验证了所提算法的性能。本文初步探索了利用深度强化学习实现多域联合干扰规避的方法，未来可以考虑利用DQN 等其他深度强化学习算法实现多域联合干扰规避，或者利用多智能体深度强化学习实现多节点协同干扰规避。