开链式机械臂DH 建模思路

2022-02-10徐红鑫

装备制造技术 2022年11期

徐红鑫，慕丽

（沈阳理工大学机械工程学院，辽宁沈阳 110000）

0 引言

机械臂能模仿人手和手臂的某些功能，虽然不如人体手臂灵活，但在三维空间，四到六个自由度就能满足三维空间的简单工作，例如用以按固定程序抓取、搬运物件或操作工具的自动操作装置。他可以代替人的繁重劳动以实现生产的机械化和自动化，能在不利于人身安全的环境完成工作目的，因而广泛应用于机械制造、冶金、轻工业等各个领域。随着一些工业和航天行业的发展，对机械臂运动控制系统的精度要求越来越高，相关技术也引起了人们广泛的关注，其中重要的一环就是机械臂运动学的建模以及求解[1]。

运动学从工作需求以及功能上可分为正运动学以及逆运动学，正运动学为通过给定各个关节的角度而求出机械臂上任意一点（主要是末端执行器）的位置以及姿态。逆运动学为通过给定末端执行器的位置以及姿态，计算各个关节能够实现这一要求的运动量。其中逆运动学是运动学建模以及求解的关键也是难点[2]。机械臂的正运动学模型为机械臂递归动力学控制的每一步提供了各个连杆的质心位置以及关节位置，而机械臂的逆运动学与机械臂的轨迹规划是密不可分的。

由于工程中绝大多数机械臂都是串联结构，故主要讨论该结构类型的建模思路，以及常用建模方法和求解方法。

1 传统DH 与改进DH

1.1 两种建模方式的发展

DH 系及DH 参数表示了用关节连接的相邻两根杆件间的坐标系及坐标参数。其中a，c，琢为结构参数，定义了相邻两个关节间的固定值，准为运动参数，表示关节的运动量。 Craig 后来介绍了建立改进DH系的方法。改进DH 系与传统DH 系的不同之处在于，DH 参数与杆件之间的对应关系成为主要目标，而DH 参数与关节之间的对应关系被视为次要因素。改进DH 系在理论推导时物理意义更加明确，方便工程人员应用[3]。

1.2 DH 建模与改进DH 建模对比

在机械等相关领域书籍中，定义关节与连杆的方法如图1 所示，在串联机械臂结构中，操作臂通常都是由转动关节和移动关节组成的，基座称为连杆0，不包含在连杆之内，连杆1 和基座由关节1 相连，连杆2 和连杆1 由关节2 相连，以此类推。

图1 机械臂简图

1.3 两种方法建系区别

如图2 所示，连杆坐标系建立的位置不同，SDH方法将连杆i 的坐标系固定于连杆的远端，MDH 方法将连杆的坐标系固定于连杆的近端。

图2 关节连杆简图

SDH 与MDH 比较：

（1）固连坐标系不同

SDH 方法关节i 上固连的是i-1 坐标系，即坐标系建在连杆的输出端；MDH 关节i 上固连的是i 坐标系，即坐标系建在连杆的输入端。

（2）执行变换的顺序不同

按照SDH 方法变换时四个参数相乘的顺序依次为d-兹-a-琢，而MDH 方法则按照琢-a-兹-d（正好与SDH 相反）

2 改进DH 建系思路

在相关教材中少有解释改进DH 建模的具体思路。虽然思路并不固定。但是都大同小异，都是通过依次建立三个坐标轴的方法。但是建立坐标轴的方式并不唯一，且一般错误的原因都是坐标原点的选择错误，而不是坐标系的选择错误[4]。

2.1 自由度

如图3 所示：在三维空间中，每一个物体都有六个自由度，分别为沿着空间坐标三个轴的双向移动和绕着三个轴的双向旋转。即空间中任意两个物体，能够精确掌握二者之间三个坐标轴方向的距离差和角度差，就能够掌握二者的相对位置关系。将空间中的物体都固接一个三维直角坐标系，则直角坐标系相对于大地坐标系的位置和姿态都可以表示出来。如图所示坐标系A 与坐标系B 不仅有空间上位置的差别，还有自身角度即姿态的差别，坐标系A 要通过三个坐标轴方向的平移以及绕三个坐标轴方向的旋转才能与坐标轴B 重合[5]。

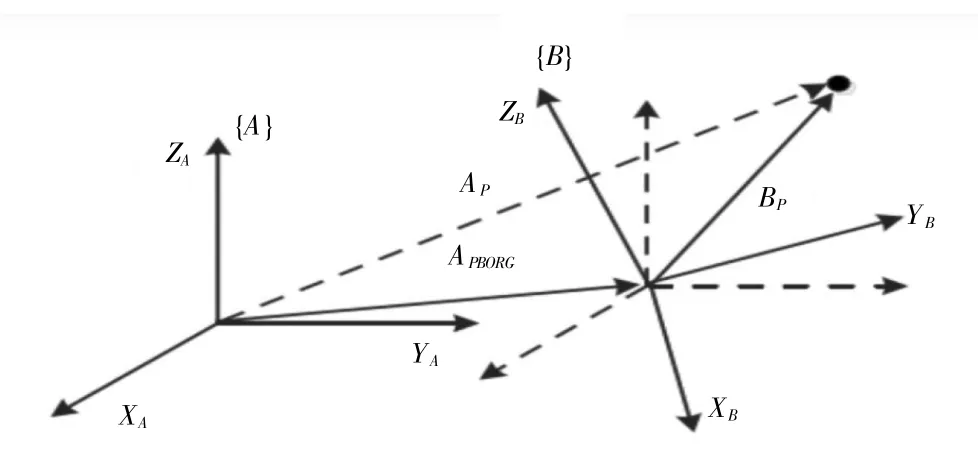
图3 位姿变换简图

为了方便计算DH 参数，将空间的六种自由度表示为空间两物体的六种相对位姿关系。

（1）坐标系A 的原点到坐标系B 的XOY 平面的最短距离即坐标系B 的Z 轴方向上的距离。

（2）坐标系A 的原点到坐标系B 的XOZ 平面的最短距离即坐标系B 的Y 轴方向上的距离。

（3）坐标系A 的原点到坐标系B 的YOZ 平面的最短距离即坐标系B 的X 轴方向上的距离。

（4）坐标系A 的X 轴绕自己的Z 轴旋转至与坐标系B 的Z 轴同向的角度，即Z 轴方向上的旋转角度。

（5）坐标系A 的Z 轴绕自己的X 轴旋转至与坐标系B 的X 轴同向的角度，即X 轴方向上的旋转角度。

（6）坐标系A 的X 轴绕自己的Y 轴旋转至与坐标系B 的X 轴同向的角度，即Y 轴方向上的旋转角度。

2.2 改进DH 建系思路整理

由于串联式机械臂的特性，机械臂可以看作成为一个开式运动链，它由一系列连杆通过转动副或者移动副串联而成，开链的一段固定在基座上，另一端是自由的，安装着末端执行器，完成各种作业。关节由驱动器驱动，关节相对运动导致连杆的运动，所以研究机械臂连杆的位置关系可以转化为研究关节的相对位置与姿态。将每一个关节固定一个坐标系，然后描述这些坐标系之间的关系。

以puma560 机械臂为例，如图4 所示：这是典型的六自由度串联式机械臂，基座称为连杆0，其中末端的三个旋转轴可理解为球形关节，具有三个自由度，相当于人类的手腕部，建立坐标系分如下几部。

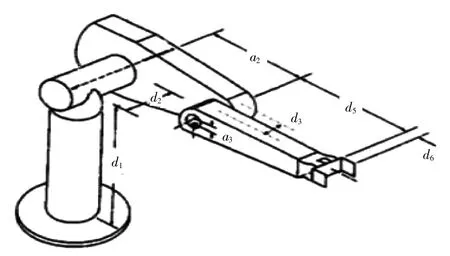
图4 PUMA560 机械臂

（1）绘制机械臂结构简图，找出影响实际操作工作的连杆与关节轴，如图5 所示。

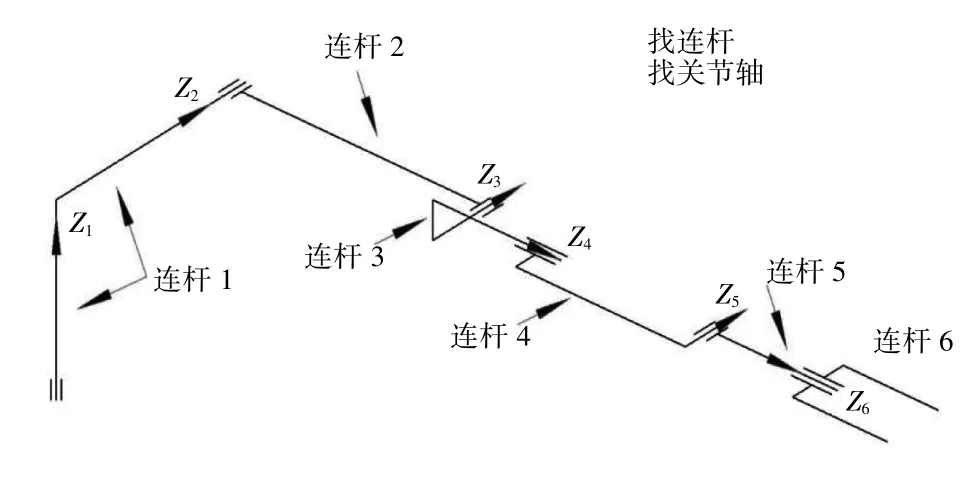
图5 PUMA560 机构简图

由于机械臂实际形态，有些连杆的结构形状特殊，例如连杆1 和连杆3。

（2）确定相邻两连杆之间的交点或者公垂线，如图6 所示，其中关节2 的轴线与关节3 的轴线相互平行，且公垂线无数条。

图6 PUMA560 原点选取

（3）确定关节坐标系原点位置：大多数教材是直接规定坐标轴的方向，由于关节2 与关节3 为平行轴，所以多个版本坐标系规定不同，切容易混乱[6]。直接规定坐标系原点位置更简洁易懂。关节i 的坐标系原点为轴线i 与轴线i+1 的交点位置，若无交点，比如两坐标轴平行时，可为了使坐标系i 与坐标系i+1的两个z 轴和两个x 轴位置更加特殊而随意选取。

（4）确定关节坐标系3个轴方向。

如图7 所示：坐标系i 的z 轴为坐标系i 的轴线方向。

图7 PUMA560 坐标轴选取

坐标系i 的x 轴为沿着轴线i 与轴线i+1 的公垂线，指向关节i+1。若轴线i 与轴线i+1 相交没有公垂线，则坐标系i 的x 轴应垂直轴线i 与轴线i+1 做构成平面，方向由右手定则决定。y 轴同理也由右手定则决定。

其中基座坐标系指固定于机器人基座上的坐标系，这个坐标系是一个固定不动的坐标系，因此在研究机械臂运动问题的时候，可以把该坐标系作为参考坐标系，可以在这个参考坐标系中描述操作臂坐在其他连杆坐标系的位姿，为了使问题简化，通常将该坐标系与坐标系1 相重合。

（5）获取dh 参数

如图8 所示：由于机械臂各个关节所固接的坐标系的特殊，坐标系i-1 并不需要六种坐标变换才能与坐标系i 重合，即通过3个轴的移动以及绕三个轴的旋转。图8 的两轴位置比实际机械臂的位置更特殊，更具有意义[7]。

图8 关节简图

淤坐标系i-1 先进行绕自身x 轴的旋转，转至坐标系i-1 的z 轴与坐标系i 的z 轴同向；将两关节之间依靠该运动所需要的角度计为琢。

于坐标系i-1 沿着两轴公垂线即坐标系i-1 的x轴的方向平移，直至坐标系i-1 的z 轴与坐标系i 的z 轴位于同一条线，所需矢量位移计为a。

盂坐标系i-1 沿着z 轴方向做平移直至两坐标系原点重合，所需矢量位移计为d。

榆坐标系i-1 绕z 轴旋转直至两坐标系完全重合，所需矢量角度计为兹。

3 奇异性

30年前的S.hayatl 的论文提到了传统的DH 的奇异性的问题，但是这种奇异性既不是空间变换矩阵是否可逆的问题，也不是我们常说的机器人运动学的奇异性问题。而是DH 坐标系定义的奇异性。

由于在运动学建立坐标系中是针对机器人运动学参数进行标定的，所以机器人实际结构参数可能会存在偏差。对于一般关节来说问题不大，但是对于两个相邻平行关节时，DH 坐标的x 轴方向定义不明确。

在定义DH 坐标系时，从上文可以得出DH 建系的方法只有4 种变换，缺少y 轴方向的平移和绕y 轴方向的旋转。在建立坐标系时，相邻平行的关节，由于加工或者装配上的误差，2个平行的轴实际上绝对位置是有小范围误差的，由于建立坐标系时x 轴定义为相邻轴线的法线方向；所以轴向的小范围误差就可能会导致dh 坐标系中x 轴方向上的大范围误差。

4 奇异性解决方法

（1）传统方法

引入修正系数茁，描述为绕y 轴的旋转，既然两个平行轴间有微小差距，坐标系i 通过正常的变换无法与坐标系i+1 重合，加入新的自由度，即绕y 轴的旋转使其重合。在正常变换中，最后一部为绕z 轴旋转使两坐标系完全重合，由于两轴实际不平行，所以无法通过该变换使其重合。通过修正系数，当两坐标原点重合时，先进行绕y 轴的旋转，使两z 轴重合，再进行z 轴的旋转使其完全重合。因为建系原则不变，坐标系i 的x 轴依然垂直两坐标系轴线，所以当原点重合时，可以通过绕自身y 轴的旋转达到两坐标系z轴重合的效果。

（2）改进方法

引入新的参数L 表示y 轴方向的平移。旋转在矩阵变换的计算量是要大于平移的，利用此特点将两个平行的关节靠近基座的关节的坐标轴的x 轴与y 轴互换，则坐标轴i 可通过平移先与坐标轴i+1 重合，原来的先绕y 轴旋转再绕z 轴旋转就变成了先绕x轴再绕z 轴，和其他相邻关节的旋转变换达成统一，相比于S.hayatl 提出的旋转参数修正方法，不仅修正效果完全等效，平移参数的修正方法在形式和计算上更为简单，易于处理。