微拓扑参数下双箭头三星型复合微结构面内冲击性能研究①
2022-02-10杨洪涛李云伍赵颖
杨洪涛,李云伍,赵颖
西南大学 工程技术学院,重庆 400715
微结构材料具有优异的吸能特性,被广泛应用于各类吸能部件中[1],研究在冲击载荷下微结构材料的动力学响应特性和吸能特性显得尤为重要.
微结构材料在不同微拓扑参数下会呈现出不同的性能. 相比于正六边形蜂窝,负泊松比(Negative Poisson’s Ratio,NPR)材料呈现更高的抗压强度和更强的吸能特性[2],元胞壁厚、元胞角度及层数也会对蜂窝材料的抗冲击和低频隔振性能产生影响[3],随着壁厚的增大,正八边形多胞材料的比吸能逐渐增大[4]. 马芳武等[5]研究了不同倾斜角度和不同冲击速度对微结构材料变形模态和动力响应的影响. 张新春等[6]通过改变微元胞高度,进而改变微结构材料的相对密度,研究发现在相同冲击速度下,相对密度越大,平台应力越大,同时不同的构型也会对微结构的动态性能产生影响. Qiao等[7]提出了一种以棱边形状为正弦曲线的微结构,并采用单胞法分析了其动态响应和性能;王博等[8]对比分析了正四边形与星形两种微结构的力学性能,得出正四边形微结构的各项力学性能均优于星形微结构;Warren[9]通过改变六边形夹角及边长,构建了多种构型六边形蜂窝的有限元仿真模型,最终得出正六边形的动态响应最优.
以上大部分研究主要聚焦于单种类型微元胞,对复合类型微结构的研究较少,因此,本文提出一种新型双箭头-三星型(Double Arrow-Tristar,DAT)复合微结构,如图1所示. 该DAT复合微结构的代表性微元胞由1个双箭头和1个三星型微元胞在水平方向上重复排布、竖直方向上周期性交错排布而成. 由于微拓扑参数(如微元胞长度、胞壁厚度、微元胞夹角等)对该DAT复合微结构的动力学性能起决定性作用,因此,研究微拓扑参数对其动力学特性的影响是非常有意义的.

图1 DAT复合负泊松比微结构代表性微元胞
图1为该DAT复合微结构代表性微元胞结构示意图,M和N分别代表双箭头微元胞长短胞壁的长度,P为三星型微元胞胞壁长度,H和K分别代表双箭头、三星型微元胞高度,Q=βM为微元胞水平胞壁的长度,φ为双箭头微元胞的长胞壁与轴线的夹角,η是三星型微元胞胞壁与轴线的夹角,且φ=2η.TL为微元胞壁厚度,TL=αM,其中,α和β分别为厚度系数和长度系数,微结构参数如表1所示.

表1 微结构参数值
1 计算模型
1.1 有限元模型建立
面内冲击荷载作用下该DAT复合微结构的计算模型如图2所示. 试件尺寸为L1×L2=180 mm×286 mm,微元胞夹角分别采用φ=20°,φ=30°,φ=35°和厚度采用TL=2 mm,TL=1.5 mm不同组合的DAT复合微结构进行填充,如图3所示. 微元胞夹角φ=20°,φ=30°,φ=35°的微结构在y,x方向的排列数目分别为6×14,6×11,6×9. 其中,基体材料采用铝合金,杨氏模量E=69 GPa,泊松比μ=0.34,屈服应力σys=462 MPa,密度ρ=2 750 kg/m3.

图2 DAT复合负泊松比微结构面内冲击模型

图3 不同夹角下DAT复合负泊松比微结构有限元仿真模型
采用显式动力学软件LS-DYNA对其进行动态性能仿真分析. 在计算过程中,赋予截面属性为SECTION_SHELL,设置计算单元积分的方式为Belytschok-Tsay,横向剪切应力缩放系数为2,厚度方向积分点为3,沿z轴方向厚度为2 mm. 同时计算中施加约束条件,保证变形平面的应变状态,模型中所有节点面外位移均被限制[10],且刚性墙沿y轴负方向冲击该DAT复合微结构,模型底端固定,并对其面内自由度进行约束,对底部固定端进行六自由度全约束.
1.2 模型可靠性验证
1.2.1 准静态压缩试验
为验证所建立有限元模型的可靠性和准确性,对该DAT复合负泊松比微结构样件进行准静态压缩试验,如图4所示. 该样件由3D打印制造而成,基体材料采用ABS工程塑料,其密度ρ=1.05 g/cm3,泊松比v=0.33,弹性模量E=2 GPa. 试验台加载速度设置为10 mm/min,y与x方向代表性微元胞分别为6个和10个.

图4 准静态压缩试验
建立与准静态压缩试验相同的有限元计算模型,对该复合微结构的面内动态响应进行分析. 若按照与准静态压缩试验相同的速度加载,计算过程很费时间,因此可通过提高加载速度的方法来缩短计算时间. 提高加载速度后需保证动能与总能量之比、沙漏能与总能量之比均在5%以下[11],这样就可保证准静态压缩过程与试验过程相对应,图5为该DAT复合微结构在面内冲击作用下的动能曲线、内能曲线、总能量曲线、滑移能曲线和沙漏能曲线. 从图中可看出,在整个冲击过程中,内能和动能的变化量可以反映出系统的总能量守恒,并且沙漏能为5%,远远小于总能量,满足模型验证的基本要求,进一步验证了仿真模型的准确性和可靠性.

图5 该DAT复合负泊松比微结构在面内冲击载荷下的能量曲线
1.2.2 面内变形模式和应力-应变曲线
图6为冲击速度为10 mm/min下,该DAT复合微结构在不同压缩程度下试验和仿真的变形模式对比图. 通过对比可知,在基体材料性能、边界条件和加载条件完全相同的条件下,计算结果与试验结果的面内变形模式基本类似. 从变形模式中看出该DAT复合微结构的变形呈现非线性变形,失效模式为屈曲失效[12]. 同样,也可分别得到该DAT复合微结构准静态压缩和有限元仿真分析的应力-应变曲线对比图,如图7所示. 从图中可看出,两条曲线趋势一致,仿真分析结果与试验结果相近,从而更进一步验证了有限元仿真模型的准确性和可靠性.

图6 DAT复合负泊松比微结构沿y轴冲击下的面内变形模式

图7 准静态压缩试验和有限元仿真分析应力-应变曲线
1.3 相对密度定义
微结构材料相对密度为代表性微元胞最小单元内胞壁的面积与最小单元的总面积之比,如图8所示. 因此,该DAT复合微结构的相对密度表示如下:

图8 DAT代表性微元胞相对密度示意图
(1)
式中,S1为该复合微结构代表性微元胞最小单元内胞壁的面积,S2为最小单元面积.
经计算,该DAT复合微结构的相对密度可由下式得到:
(2)
在微拓扑参数中,胞壁厚度和微元胞夹角对相对密度的影响较大[13]. 因此,本文保持长度系数和高度不变,通过改变微元胞夹角及胞壁厚度来讨论其对面内动态性能的影响.
1.4 临界速度模型建立
当冲击速度超过陷波波速[14]时,微结构材料的变形开始由整体变形向局部变形转变,陷波波速称为第一临界速度,即:
(3)
式中,εcr表示该DAT复合微结构的初始应变,即应力达到第一次应力峰值时所对应的应变,E为所选微结构材料的弹性模量,ρRD为所选微结构材料的相对密度,Δρ为所选微结构材料密度.
随着冲击速度的增加,受冲击载荷影响,微结构材料所产生的局部变形带由冲击端向固定端传播. 经验公式[14]给出了微结构材料局部变形带形成的临界冲击速度,称为第二临界速度.
(4)
式中,σys为所选材料屈服应力,εd为所选材料密实应变. 根据表2,当TL=1.5 mm,φ=30°时,取相对密度ρRD=0.284 3,代入式(3)和式(4),可得该复合微结构的第一临界速度Vcr1≈12.14 m/s,第二临界速度Vcr2≈71.32 m/s. 基于此,本文选取冲击速度分别为8,20,50,90 m/s,并研究不同冲击速度对该DAT复合微结构面内动态性能的影响.

表2 不同微结构参数下该DAT复合微结构的相对密度
2 计算结果与讨论
2.1 面内冲击响应
该DAT复合微结构在不同冲击速度和不同微拓扑参数下的部分面内冲击变形模式如图9所示. 当胞壁厚度一定时,随着微元胞角度由30°减小为20°,整体相对密度和结构刚度陡增,胞壁难以被压弯,从而使微结构提前产生完全塑性铰. 在压缩变形过程中,呈现出微元胞之间连接点转动、弯曲扭转和微元胞壁轴向受压直至密实的混合变形模式,负泊松比特性不够明显. 当微元胞夹角增加到35°时,降低相对密度可使“压缩-收缩”的负泊松比效应更明显. 当微元胞角度保持不变时,减小胞壁厚度,降低相对密度可有效提高负泊松比特性,尤其是厚度为1.2 mm时的负泊松比效应更明显. 冲击速度越大,局部变形带的产生愈明显,且在冲击端和底端同时产生并向中部靠拢,变形模式呈现“V”形且变形更加明显. 随着微元胞夹角的增加和胞壁厚度的降低,微结构达到密实形变的时间也有所增加. 此外,相对密度较大的微结构并没有呈现出稳定有序的负泊松比变形模式,而相对密度较低的模型则呈现出稳定有序的变形,具有良好的负泊松比特性.

图9 DAT复合负泊松比微结构在不同微拓扑参数下的变形模式
2.2 应力-应变曲线
与传统微结构材料不同,该复合微结构在整个压缩过程中的应力-应变曲线图可分为4个区域:弹性区、平台区、平台应力增强区和密实化区. 其上下两种不同构型微元胞的组合使其在动态响应中会出现两个弹性区和两个平台区,这也是该DAT复合微结构的特殊之处. 在弹性区(ε=0~0.05,ε=0.3~0.35),其变形形式主要是胞壁弯曲形变,该区域的曲线斜率较大甚至趋近于直线,主要是由于随着应变率的增加,微元胞夹角逐渐减小,胞壁之间相互接触形成新的支撑,结构刚度逐渐增大. 图10为不同微拓扑参数下该DAT复合微结构的应力-应变曲线,当胞壁产生完全塑性铰时,应力-应变曲线进入一段相对平缓区域,称为平台应力区,此时,应变处于ε=0.05~0.3和ε=0.35~0.6范围内. 在第一个平台区(ε=0.05~0.3),三星型微元胞率先出现负泊松比效应,接着双箭头微元胞产生变形,即出现第二平台区(ε=0.35~0.6). 当应变ε=0.6~0.8时,微结构向外扩张并趋于密实,逐渐填满所有孔隙,且刚度逐渐增大,该区域称为应力增强区. 当全部微元胞都发生坍塌后,相邻微元胞胞壁完全接触,孔隙几近消失,相对密度陡增,从而使其刚度变大,应力-应变曲线的斜率接近其弹性模量.

图10 不同微拓扑参数下该DAT复合微结构应力-应变曲线
从图10可看出,当胞壁厚度TL=1.5 mm和TL=1.2 mm时,冲击速度越大,平台区应力值会有些增加,冲击速度越低,双弹性区、双平台区的划分愈明显,整体曲线呈越来越均匀稳定的趋势. 当胞壁厚度TL=2 mm时,该DAT复合微结构的平台区应力分布明显提高,整体应力增大. 由于相对密度减小,平台区的压缩过程将会延长,孔隙被挤压的应变增大. 因而,厚度小的复合微结构所对应密实区应变出现的时间略有滞后. 当夹角增大至φ=35°时,TL=1.2 mm的高应变率整体应力分布偏大,表明其具有良好的吸能特性. 当进入第二平台应力区(ε=0.35~0.6),除φ=35°外,其余应力水平保持一致. 在应变增强区(ε=0.6~0.8),微元胞夹角φ=35°下复合微结构的应力增强要高于微元胞夹角φ=20°的应力增强.
2.3 平台应力分析
该DAT复合微结构的平台应力可表示如下:
(5)
式中,εcr为屈服应变;εd代表名义平台应力增强区向密实应变区转化时的应变.σ(ε)为随名义应变而变化的名义应力. 平台应力被定义为平台区应力的平均值. 基于公式(5),可得到不同结构参数和不同冲击速度下的平台应力值,分别如表3和图11所示.

表3 不同结构参数下该DAT复合微结构的平台应力 MP
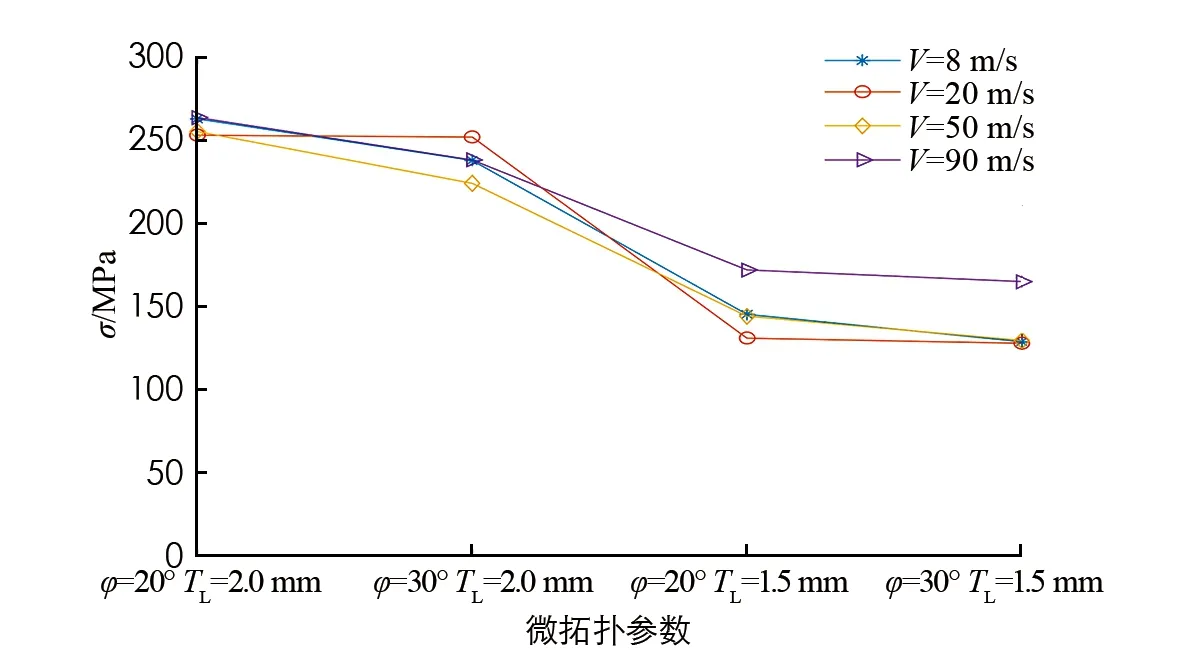
图11 不同微拓扑参数下该DAT复合微结构的平台应力曲线
从图11可看出,冲击速度为8 m/s,20 m/s时对平台区应力的影响较小,曲线保持一致且整体应力水平不如高速时显著. 除φ=35°,TL=1.2 mm以外,在冲击速度50 m/s和90 m/s下,速度的增大会使平台应力值整体增加,这是由于冲击速度的增加会导致材料的惯性效应增强. 当冲击速度相同时,φ=20°,TL=2 mm时的平台应力值最大,φ=30°,TL=2 mm下的平台应力次之.
综上所述,随着相对密度的增大,局部变形带会更加明显,且随着刚度的增加和孔隙率的降低,使平台应力水平明显增加,也表明了相对密度越高,该DAT复合微结构具备良好的吸能特性. 由表2与表3还可得出平台应力正比于该DAT复合微结构的相对密度,但过高或过低的相对密度都会使该DAT复合微结构的整体应力水平和吸能特性大幅降低.
2.4 吸能特性分析
该DAT复合微结构单位体积吸能量可由下式表示:

(6)
式中,压缩应力σ(ε)是应力-应变曲线函数,εd为微结构材料从应力增强区向密实区转化的应变率,可由数据中密实应变区的应力峰值确定应变率数值. 图12为该DAT复合微结构在相同微拓扑参数、不同冲击速度下的吸能曲线.
从图12可看出,随着应变率的增大,吸能曲线呈整体上升趋势. 当TL=1.5 mm和TL=1.2 mm时,冲击速度90 m/s所对应的吸能曲线基本都位于最上方. 微元胞夹角φ=30°时所对应的吸能曲线相近. 通过曲线表明,应变率对该DAT复合微结构的变形和吸能特性有直接的影响. 基于变形模式进行分析,在较高应变率下,其吸能主要归功于冲击端附近的局部变形带;而在较低应变率下,其吸能主要归功于固定端附近的局部变形带,因此,冲击速度8 m/s下的平台应力增强区更明显,吸能特性更强.

图12 不同微拓扑参数下DAT复合微结构吸能曲线
同理,图13为该DAT复合微结构在不同微拓扑参数、相同冲击速度下的吸能曲线.
从图13可看出,当冲击速度保持不变时,该DAT复合微结构在相同应变下的吸能曲线随着微元胞夹角的减小而增加,胞壁厚度的增加而增加,整体呈上升趋势,其中,TL=2 mm,φ=20°时的吸能曲线位于最上方,吸能特性最强,该结论与图10和图11所呈现的结果一致.

图13 不同冲击速度下DAT复合微结构吸能曲线
该DAT复合微结构的吸能曲线有两个拐点,第一个拐点代表平台应力增强区的开始,胞壁之间开始相互接触形成支撑. 第二个拐点代表该复合微结构应力增强区的结束和密实化区的开始. 结合变形模式分析可知,随着厚度系数的增大,微元胞夹角的减小,相对密度的增大和结构刚度的增大,该复合微结构进入密实应变的时间提前,等效平台应力越来越大,且吸收能量也越来越高. 但当其相对密度很大时,密实化应变值会非常小,吸能量也越低,而相对密度过小时又会削弱其吸能特性,图12中TL=1.2 mm,φ=35°时的吸能量仅为TL=2 mm,φ=20°的1/8.
3 结论
本文提出一种新的DAT复合微结构,首先采用准静态压缩试验对模型可靠性进行了验证. 其次,采用有限元软件HyperWorks和显式动力学软件LS-DYNA详细分析了微拓扑参数和冲击速度对其面内冲击变形模态和吸能特性的影响. 主要结论归纳如下:
1)建立了微拓扑参数(胞壁厚度和微元胞夹角)与变形模式之间的关系. 微拓扑参数的不同改变了其变形模式和应力分布,同时,研究了同一冲击速度下不同微拓扑参数对该DAT复合微结构动态响应的影响. 结果表明:厚度系数的增大和微元胞夹角的减小以及相对密度的增大使微结构材料的等效平台应力越来越大,负泊松比现象趋于不明显.
2)建立了微拓扑参数与该DAT复合微结构吸能特性之间的关系. 随着相对密度的增大(即厚度系数的增大,微元胞夹角的减小),胞壁之间形成相互支撑,接触更密实,且密实应变率范围更大,使该复合微结构在平台应力区、应力增强区及密实应变区所表现的吸能特性提高.
3)该复合微结构具备“压缩-收缩”的变形模式,不同于单一形状的微结构,其还具有双平台区的动态响应,通过调节微拓扑参数还可得到力学性能更优的微结构材料,为其在工程领域的实践应用提供了数据支持.
