异质预期下双寡头企业碳减排决策的复杂性分析

赵刘威, 金 帅, 姜鸿运, 彭振革

(1.江苏理工学院 管理学院,江苏 常州 213001; 2.江苏大学 管理学院,江苏 镇江 202013)

0 引言

当下全球温室效应日趋严重，发展低碳经济、节能减排已成为全球各个国家及地区促进全球经济可持续发展的重大战略举措之一[1]，相继出台各种有关环境政策规制来促进企业进行碳减排，以求降低碳排放。我国作为世界大国，一直对全球环境保护的发展保持高度的支持态度，并在巴黎的第21届气候大会上向全世界承诺到2030年单位GDP的二氧化碳要比2005年时下降60%～65%。为完成此目标，2019年党的十九届四中全会及“国民经济和社会发展第十三个五年规划纲要”均对环境保护新形势新格局做出新要求，提出绿色低碳循环发展产业体系和清洁低碳、安全高效的现代化能源体系，低碳发展目前已经成为我国当代的主旋律。

鉴于减排政策对于减排目标实现的重要性，基于政策选择的情景分析以及相应的政策成本评估成为理论研究的前沿与焦点[2]。例如，石敏俊等[3]基于动态CGE模型分析了碳税、碳交易以及碳税与碳交易组合等不同政策的减排效果、经济影响与减排成本，并提出组合政策是较优的政策选择，可以确保减排目标的实现与降低行业减排压力。段宏波和杨建龙[2]系统考察了基于碳定价和补贴的政策组合选择对2030年碳达峰和非化石能源发展目标的差异化影响。Bi等[4]运用动态CGE模型探讨了碳市场、碳税以及两者组合下碳减排政策的内在技术激励差异所引起的绿色发展路径的差异。Cao等[5]对中国碳排放交易的动态CGE模型模拟研究同样表明碳税和碳交易组合机制能够以更低的碳价与福利成本实现相同的国家减排目标。肖谦等[6]基于电力部门细分的递推动态CGE模型模拟了实现2030年国家自主贡献目标背景下不同碳交易政策组合情景的经济影响。总体而言，相关研究主要以实现国家碳减排目标为背景，从宏观层面采用CGE模型展开分析，并认为碳税和碳交易在我国可以共同发挥作用促进减排目标的实现[6]。

同时，鉴于企业作为市场经济的主体更是国家推进减排目标实现的重要落实对象，基于微观行为视角的减排政策对企业的影响、企业最优决策以及规制优化研究也愈发得到学界关注；相应地，经典博弈论与优化理论也被广泛采纳以揭示碳减排问题内在规律与微观机理。例如，Mandell[7]运用扩展的Weitzman“价格与数量模型”，从效率的角度论证了采取碳交易和碳税政策比实行单一政策拥有更好的减排效果和经济效率。张国兴等[8]运用信号博弈理论构建了企业与政府节能减排模型，探究了补贴额、违规成本等最优边界。王明喜等[9]从微观生产过程出发，基于成本最小化模型剖析了碳排放约束下碳排放配额对企业最优减排投资的影响。赵黎明和殷建立[10]建立了一个由政府作为负责碳减排总体计划和控制的上层决策者以及企业作为拥有碳减排自主决策权的下层决策者所构成的碳减排二层规划决策模型，以解决复合型政策情景下政府和企业在平衡减排与低碳效益之间的关系权衡。曹细玉和张杰芳[11]构建供应链博弈模型考察了碳税和碳减排补贴下的供应链碳减排决策优化与协调问题。Zhang等[12]则研究了碳交易和碳税组合政策下处于垄断地位的耐用品制造商对出售与租赁两种营销模式的最优选择问题。由于高碳行业的特殊性，寡头市场结构被广泛应用于碳减排问题的研究中[13,14]。Orlov和Grethe[13]基于改进的STAGE模型研究了在产品市场完全竞争和古诺寡头垄断情况下碳税对俄罗斯经济的经济影响。Wang和Zhou[14]通过构建Nash-Cournot寡头垄断市场均衡模型研究了碳配额分配对碳成本转嫁率的影响。Creti和Sanin[15]研究表明竞争性的碳交易市场也会对污染性古诺企业产生合并激励，并较好解释了美国RGGI与欧盟EU-ETS规制下电力行业合并的动因。

总体而言，近年来碳减排研究领域涌现出了丰硕成果，并为碳减排政策工具的选择提供了较为坚实的理论支撑。但是，关于企业碳减排的研究通常建立在标准的理性个体行动模型之上，并因此引发了其尚不足以支撑政策分析的质疑[16]：假设同质和理性的经济参与者[17]，而忽略了参与者的有限理性[18,19]，及其对参与者的多样化行为策略以及与其他参与者的相互作用；相关研究强调对于均衡结果的考察，但相对忽视了对均衡形成过程以及动态调整过程和动态环境下均衡稳定性的关注[20,21]。实际上，由于对现实的解释力不足，主流经济学所依赖的完全理性假设愈发遭受理论界的质疑，相对地，有限理性假设更贴近现实[22]；同时，企业所面临的碳减排体系与产品市场是一个复杂的系统，而企业的“有限理性”意味着他们无法确定实现目标的最佳行动方案，需要经过不断的调整才能适应通常无法预测的变化[17,23]；更重要的，受到外在和内在环境的影响，现实经济主体在行为和能力方面也是异质的[24]，企业之间很难做到相同预期，决策过程并不符合新古典经济学的最大化和均衡假设。异质预期是经济学家William A. Brock于1997年最早提出[25]，并已成为现代预期管理的理论基石；其核心思想是，现实经济中不同行为主体会因信息不完全、认知局限、预测模型差异等形成不同的预期，这是与经典理性预期相对的；同时，他们也会根据结果变化反馈学习而改变自身行为；相应地，经济结果取决于所有经济主体的预期，预期的异质性则是经济波动的关键因素[26]。异质预期可以直接触发碳减排市场的起伏，所引起的波动表现为由需求驱动的金融市场或实体经济波动，或者减慢供给冲击消失的速度。更为重的是，当预期异质性积累到一定程度后，整个碳减排经济体系会产生爆炸式行为，远离稳定增长路径，陷于无效的、分散的多重均衡中。已有学者明确指出在碳减排与低碳转型中应对相关利益相关主体的有限理性与异质性行为特征予以充分的关注，以洞察其对实现可持续低碳转型造成的障碍[27,28]。

综上所述，在现有研究基础上，本文做了如下扩展：(1)同时考虑参与者异质预期与有限理性下，从动态复杂性视角研究了双寡头企业的碳减排决策；(2)引入碳减排交易机制，以经济成本和碳交易成本最小化为目标，研究异质预期下企业碳减排的动态复杂性影响。本研究可为政府在设定碳限额方面及促进企业在碳减排、发展和稳定碳交易市场方面提供更贴近现实的理论依据。

1 问题描述与模型建立

在碳税+碳交易机制下，在高碳、碳密集型行业中垄断现象尤为突出，如能源领域、电力、航空等，其中电力行业在我国只有中国电网与南方电网垄断。在现实经济活动中，企业的决策行为很容易受到外在和内在环境的影响。因此，本文考虑在特定企业碳减排决策中，双方均为有限理性且为异质预期。为了更清楚地对模型进行解释，本文结合现实情况作出如下假设：

假定两生产企业研发和生产同质的产品。每个企业的行动策略是选择各个时期的碳减排投资额，且满足要求：两参与企业在离散的时间轴上制定相应的减排投资策略。Ki(t-1)表示企业i在t-1时期的资本存量，xi(t)为其在t时期企业单期的碳减排量，减排成本系数为βi(βi>0)，所以企业单期的减排投资为βixi(t)。由于资本存在一定的折旧，投资资本存量Ki(t-1)流入下一经济时期后剩余θKi(t-1)，其中θ(0<θ<1)为折旧率。从而可得企业在相邻两时期的投资资本存量间的关系式为:

Ki(t)=θKi(t-1)+βixi(t),i=1,2

(1)

对于每个企业在某一时期所生产产品的数量，有企业投资资本积累量Ki(t)来决定其在该时期产品生产的潜能，本文用线性形式qi(t)=BiKi(t)来表示，其中正常数Bi代表企业创新生产新兴产品的技术水平。由此可得:

qi(t)=Bi(θKi(t-1)+βixi(t)),i=1,2

(2)

假设市场上该类产品的销售价格是线性逆需求函数p(t)=a-bQ(t)，其中a,b>0并且Q(t)=q1(t)+q2(t)表示两企业在市场供应量的总和。同时，企业的线性生产成本函数Ci(qi(t))=ciqi(t)(i=1,2)边际成本c1和c2均为正数。

企业在生产过程中产生的二氧化碳数量与其产量qi(t)关系，表示为kiqi(t)形式的线性关系，其中ki(ki>0)为企业的二氧化碳产生的系数。因此，在t时期，企业i单期总的碳排放量为kiqi(t)-xi(t)。每个企业在t时期拥有着一定配额的碳排放权yi(t)，则企业i的碳排放权交易量为yi(t)-(kiqi(t)-xi(t))，碳交易的市场价为p。若yi(t)-(kiqi(t)-xi(t))>0，则表示企业i出售剩余的碳排放权；反之，则需要购买不足的碳排放权，并且有

yi(t)-(jiqi(t)-xi(t))=-y(yj(t)-(kjqj(t)-xj(t)))

(3)

根据以上相关变量函数关系的假设，计算得企业i在t时期的利润为:

πi(x1(t),x2(t))=qi(t)(p(t)-ci)-βixi(t)+

p(yi(t)-(kiqi(t)-xi(t))),i=1,2

(4)

将各个变量的具体表达代入式(4)，并对πi(x1(t),x2(t))关于xi(t)求偏导，得到两企业的边际利润分别为:

φ1(t)=∂π1(x1(t),x2(t))/∂x1(t)

=P+β1(B1((a-c1-pk1)-bB2(θK2(t-1)+

x2(t)β2)-2bB1(θK2(t-1)+x1(t)β1))-1)

(5a)

φ2(t)=∂π2(x1(t),x2(t))/∂x2(t)

=P+β2(B2((a-c2-pk2)-bB1(θK2(t-1)+

x1(t)β11)-2bB2(θK2(t-1)+x2(t)β2))-1)

(5b)

本文将研究异质预期的寡头垄断博弈在每一个产出的时间周期采用不同的决策机制。假设企业1基于边际利润梯度规则，企业2在适应性预期下采用最大化的Naïve预期值。如此，企业1在t+1时期，企业增加或减少所产生的减排量主要取决于当前的边际利润是正值还是负值。故企业1随时间调整输出机制如下:

x1(t+1)=x1(t)+α(x1(t))φ1(t)

(6)

其中，α(x1(t))是正的调整函数，表示企业i基于边际利润对减排量的调整幅度。考虑线性形式的调整函数形式为α(x1(t))=αx1(t)，系数αi>0代表企业根据边际利润调整减排策略的速度。

假设企业2采取适应性预期，即在确定下一期的产量时，基于自己上一时期的产量决策与上一时期Naïve预期值进行决策，由如下等式表示:

(7)

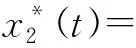
(8)

联立式(6)和(7)，并且为了表达上一致，用Ii(t)代替Ki(t-1)，显然Ki(t)替换成Ii(t+1)，得到一个如下四维离散动力学模型:

x2(t+1)=(1-β)x2(t)+

β(P+β2(B2(a-c2Pk2-bB1(θI1(t)+

(9)

离散动力系统(9)是基于市场逆需求函数和生产成本函数都是线性形式的假设，构建具有有限理性期望的博弈参与人依据边际利润调整各时期的减排策略竞争模型。

2 均衡点稳定性分析

在动力系统(9)中，令xi(t+1)=xi(t)且Ii(t+1)=Ii(t)，i=1,2得:

(10)

P-β2+B2β2(a-c2-Pk2)>0,W1>0,W2>0

(11)

在下文的分析中，非负性条件(11)均假设是成立的。

2.1 边界均衡点稳定性

要讨论动力系统(10)各均衡点(x1,x2,I1,I2)的稳定性，首先计算出其对应的Jacobian矩阵:

(12)

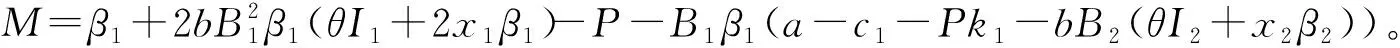
根据Schur-Cohn稳定判定条件[29]可知，当Jacobian矩阵(12)所对应的特征多项式的所有特征根都在复平面上的单位圆内，即任一特征根的模均小于1时，均衡点(x1,x2,I1,I2)是渐近稳定的。

命题1E0均是不稳定的均衡点。

证明Jacobian矩阵(12)在边界均衡点E0处的具体形式为：

通过计算得雅克比矩阵J(E0)的特征根为:

λ1=θ,λ2=1+αW1/2B2β2

由调整系数α>0和均衡点的非负性条件(11)知，后两个特征根满足λ2>1。于是，根据离散动力系统均衡点稳定判定条件知，E0是不稳定边界均衡。

2.2 内点均衡稳定性

下面主要讨论内点均衡E*的稳定性。Jacobian矩阵(12)在内点均衡E*处表达式如下:

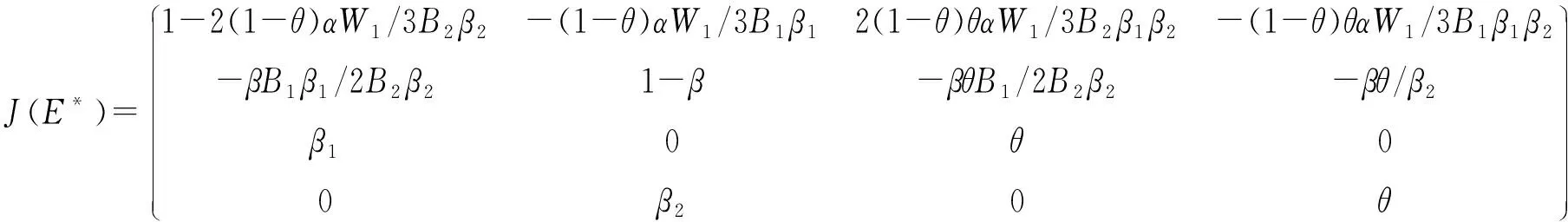
记矩阵J(E*)的特征多项式为P(λ)，且设P(λ)=λ4+p1λ3+p2λ2+p3λ+p4,则通过数值计算得多项式各项系数为:p1=β-2-2θ+2α(1-θ)W1/3B2β2,p2=1+4θ+θ2-β(1+θ)+Pα(4(θ2-1)+3β-3βθ)/3-α(1-θ)(3β-4(1+θ))β1(2B2β2+B1(P-(1+B2(a-2c1+c2-2Pk+Pk2))β2))/6B2β2,p3=3θB2β2(β-2-2θ)+2θα(1-θ)W1/3B2β2,p4=θ2。

由Schur-Cohn稳定性判定准则可知，若特征多项式也即Jacobian矩阵的所有特征值位于复平面上单位圆内，则该多项式的系数需要同时满足式Schur-Cohn稳定判定中的条件。将系统参数代入其中并化简得:

P(1)=1+p1+p2+p3+p4=αβ(1-θ)W1/2B2β2

故动力系统(9)根据Jury’s准则内点均衡E*渐近稳定，当

(13)

成立，J(E*)的所有特征值满足|λi|<1(i=1,2,3,4)。从而当满足条件(13)时，均衡点E*是稳定的。由上述的均衡点分析可知均衡点的稳定性对系统参数的取值有着依赖性。

命题2Cournot纳什均衡解E*是局部渐进稳定的，如果

α<αc=12(1-θ)(2-β+2θ)B2β2/

(1-θ)(8-3β+8θ)W1

(14)

证明由系统参数的正负性假设和条件(11)知，稳定条件中P(1)>0和1>p4显然成立。

(1-2θ+θ2+4θ3))/2(1-θ)θ

由此可知：通过以下调整速度的阈值确保纳什均衡为局部渐近稳定

从这一命题推断，纳什均衡的局部稳定性很大程度上取决于企业调整速度。特别的，如果企业过度响应(即α的值较高)，纳什均衡失去稳定性和整个系统可能会出现复杂的动力学行为。因此，分析其他数对阈值αc的影响是很有趣的，也是非常有必要的。那么，接下来将讨论β对其的影响。

对等式(14)关于β求偏导数可以得到:

∂ac/∂β=-24(1+θ)2B2β2/(1-θ)(8-3β+8θ)2W1<0

(15)

正如前面所提到的，β=1表示产出水平为最大化的纳什预期值，那么参数β的值越高，会使企业2决策者更倾向于改变前一时期产量，导致不稳定性的出现。

3 数值模拟

为了能更直观的分析模型(9)的动态行为，将运用数值仿真直观地描绘离散动力系统(9)随着模型参数变化的动态演化过程，着重分析碳交易的市场价为P和调整速度α对系统动力学性质的影响。假定参数取定值如下:a=5,b=2,c1=0.3,c2=0.4,θ=0.6,B1=0.55,B2=0.75,β1=1.2,β2=1,k1=0.4,k2=0.62,β=0.75。

图1展示在不同的调整速度α和P，使得系统(14)的纳什均衡出现震荡引起越来越多复杂的动力学行为。对比图1(a)和图1(b)发现，调整速度α的增加，Nash均衡失衡出现复杂的吸引子。对比图1(b)和图1(c)发现，碳交易的市场价P增加时，系统的Nash均衡震荡的更加剧烈。

图2给出了碳交易的市场价为P分别取P=0.125和P=0.16两种不同情况下系统(9)随着企业1调整速度α变化的分岔图。易见，在图1(a)和(b)中，随着取值的不断增大，系统由稳定于内点均衡到发生逆倍周期和逆Neimark-Sacher分岔现象，并最终进入混沌状态。图1不仅呈现了系统发生混沌现象的不同路径，还表明碳交易的市场价为越大时，状态变量的轨道进入混沌状态越早，系统具有越强的不稳定性。可以看到P的增大使得系统(9)的稳定区域减小，从而系统的动态演化更加不稳定。

图1 在不同α和P下随时间的轨迹变化图

图2 系统(9)对不同的P随调整系数α变化的分岔图

为了突显碳交易的市场价为P对动力系统(9)轨道运动稳定性的影响，在图3中描绘了不同调整系数α1取值下系统随变化而产生的分岔结果。观察图3，可分别看到逆倍周期分岔和逆Neimark-Sacher分岔现象，并且随着P的增大，系统变的更不稳定。这表明，对于碳交易的经济市场来说，碳交易市场价格增大，会增加市场上的碳库存量，从环境方面来说这是有利的，有利于促进环境保护，企业也都积极努力加大节能减排。但是在价格持续走高，影响到库存量的增加，在市场的碳库存增大到一定程度时，又引起了市场的供过于求，从而给市场的稳定性造成影响。从经济学角度来看，这一现象符合市场规律，但是从环境保护和谐发展的方面，这一现象又是一个不可取的死循环，达不到环境保护的应有的效果。

图3 系统(9)对不同的α随P变化的分岔图

图4显示，当调整速度增加时，导致纳什均衡失去稳定性，使得复杂的奇异吸引子增多的相图。图4则给出了系统轨道变化更为详细的描述，是相应于图1中轨道不同运动状态下α取值的二维相图。

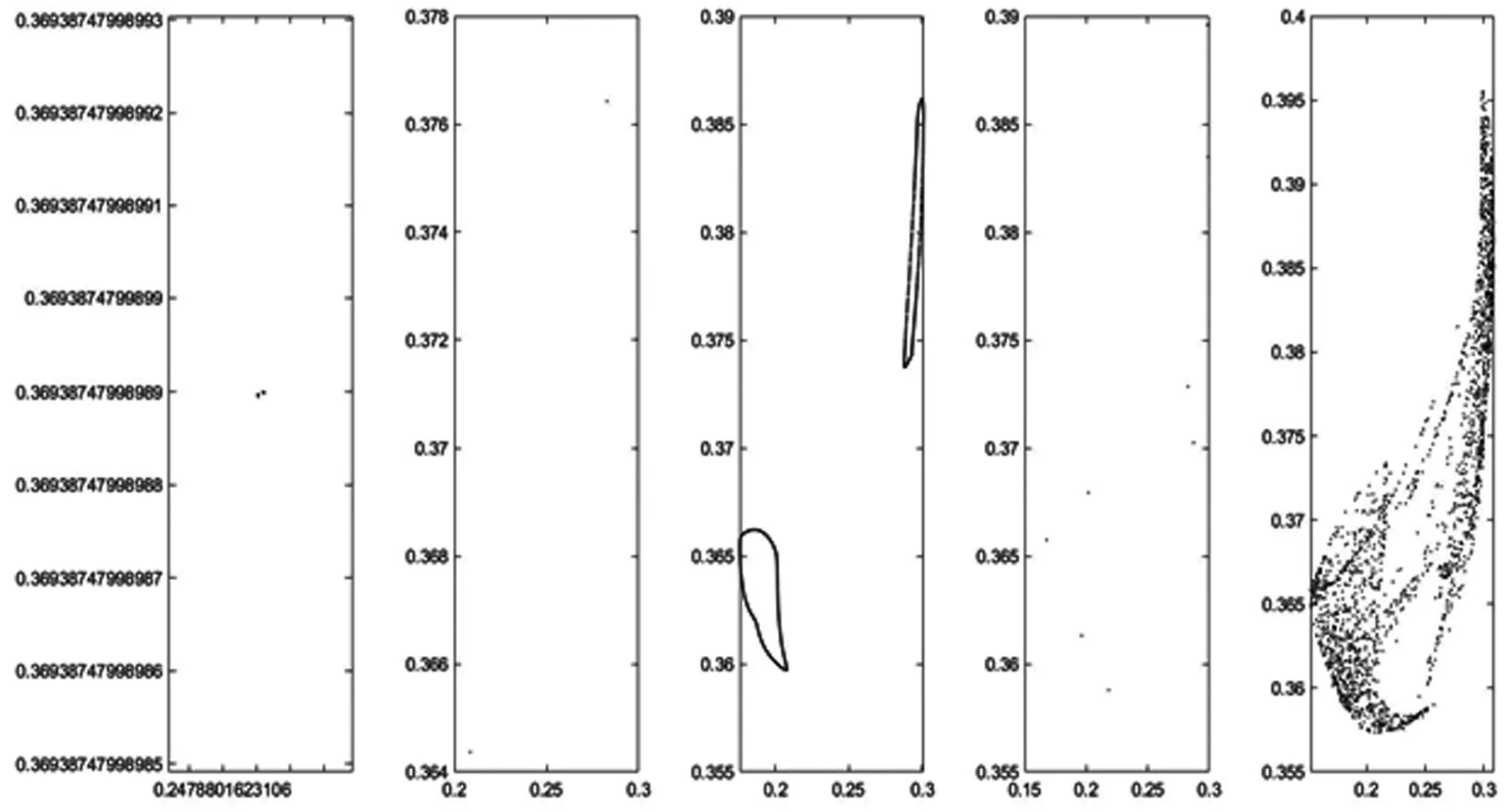
图4 p=0.125不同参数取值下对应于分岔图2的相图

选取图2(b)中系统某个混沌状态时的调整系数值α=7.23，系统初值分别为(x1(0),x2(0),I1(0),I2(0))=(0.32,0.35,0.75,0.86)和(0.32001,0.35,0.75,0.86)，绘制系统状态变量的轨道随时间的演化图形，其部分图像如图5所示。随着迭代次数的增多，同一个状态变量在两种初值条件的影响下逐渐分离并按照各自的轨道运动，即说明系统(9)对初始条件具有敏感依赖性。

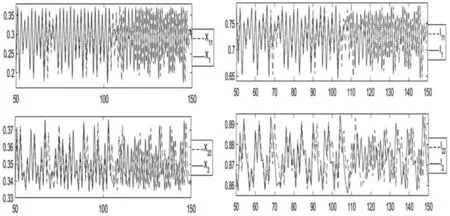
图5 动力系统(9)失稳后对初值的敏感依赖性

4 应用时滞反馈方法进行系统混沌控制

从对系统(9)演化过程的数值仿真结果可以看出，调整速度和碳交易的市场价格对系统的稳定性有着很大的影响。当垄断市场发生分叉时，两个垄断企业碳减排投入引发经济的不稳定增长，如果碳减排投入陷入混沌状态，应当立即加以控制，否则只会愈演愈烈，引发严重后果，不仅会使得市场经济恶化，陷入无序竞争中，还会使投资者产生对未来不良的预期，动摇对政府调控的信心，影响经济的稳定快速发展。因此，本文利用延时反馈控制方法对动力系统(9)的混沌行为进行控制，让其能够恢复到稳定发展状态。

如果企业通过增加一些碳减排投入来改变垄断市场的混沌状态，企业需要在每一个时刻t改变对于碳减排的投入，改变的数量与x1(t)-x1(t+1)成比例，即K(x1(t)-x1(t+1))，其中K表示调控强度。通过改变K的数值时，可以达到消除经济系统中的不稳定现象。这种方法对于企业的启示是：在出现了市场混沌的时候，需要根据这个时期与以前某一个时间碳减排投资的差额进行投资，可以实现系统长期稳定的局面[30]。化简添加控制项的系统(9)，得到如下形式受控动力系统:

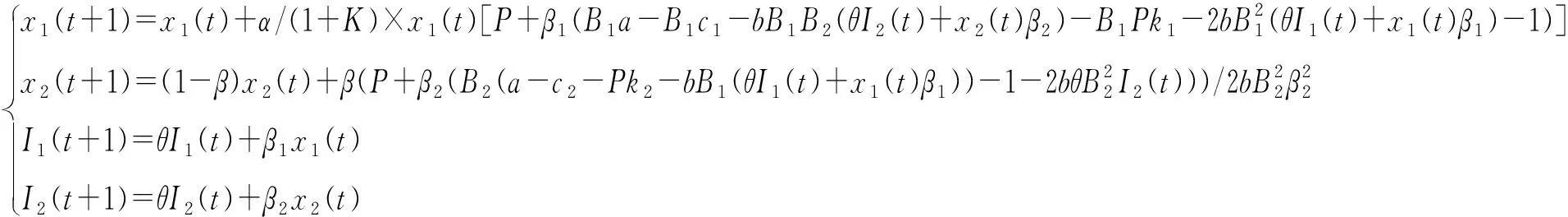
(16)

对受控系统(16)做稳定性分析。易知，受控系统与离散动力系统(9)有着相同的均衡点。受控系统(16)所对应的Jacobian矩阵为:

(17)

由图2所示，当p=0.16时，调整系数α取值约7.095，系统(9)进入混沌状态并出现杂乱的混沌现象。在原有参数取值下得到在内点均衡E*处Jacobian矩阵(16)的表达式为:

(18)

下面通过数值仿真来研究离散动力系统(9)的混沌现象受控制的有效性。观察图6，如果只在受控动力系统(9)中减排量动态迭代方程里加入反馈控制项K(x1(t)-x1(t+1))，那么只要反馈增益强度K大于0.0851就可以将不稳定的轨道控制住。图7中表示在不同增益强度下受控系统混沌行为，由初始值演化到稳定的轨道过程。通过比较可以发现，图7中K=0.2状态变量达到稳定状态的时间比K=0.09要短，碳交易市场能更快地趋于稳定状态。

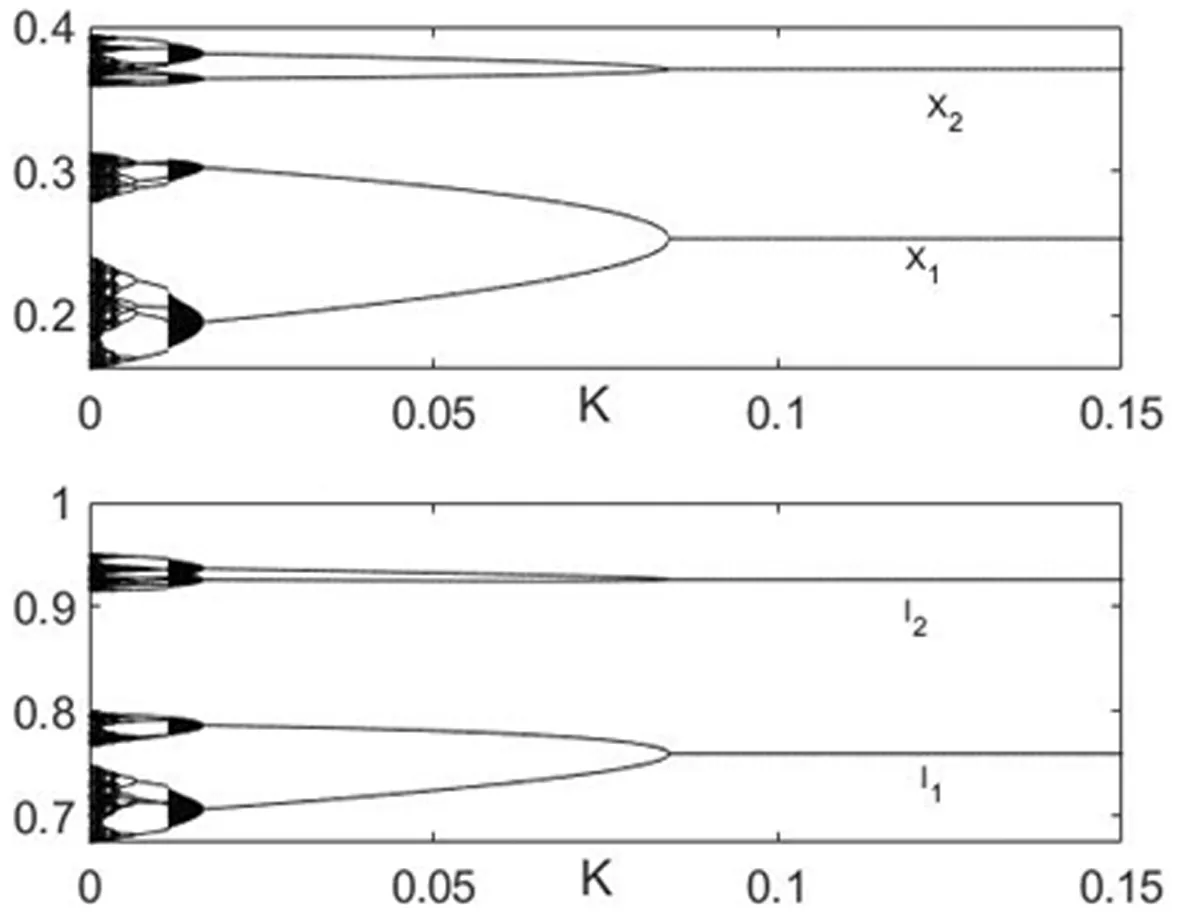
图6 系统(16)关于反馈增益强度变化的分岔图

图7 在不同增益强度下系统(16)的演化路径

5 总结与讨论

本文主要探讨了异质预期下企业碳减排投入对产出和排放水平的稳定性影响。如前文所述，鉴于某些市场结构，碳减排投入用对产出和排放的影响已经引起了相当大的关注。本文与早期论文的不同之处在于，当市场结构本身对碳减排投入水平敏感时，即当市场结构是内生的时，考虑了碳减排投入对产出和排放的稳定性影响。具体来说，随着碳减排投入改变排放水平的增加或减少，讨论了寡头垄断市场的稳定性。最后，通过延时反馈控制方法高效、快捷地将系统控制到稳定均衡状态，并且增益强度较大对控制的效果会更好。

研究发现：如果碳减排投入的调整水平随着排放水平降低，那么古诺博弈中的纳什均衡仅在某些范围的上是稳定的，超出某个阈值后将失去原有的稳定。我们注意到，只有当碳减排投入调整水平下降时结果才是稳定的。此外，这种形式的排放收费功能创造了平均成本在满足市场需求的产出范围内下降的条件，因此也创造了自然垄断存在的条件。确定排放收费的效率要求收费反映排放的边际外部损害成本，如果破坏成本按照通常的假设在排放水平上增加，则排放费用应在排放中增加。那么为什么要减少排放费用呢？从经验上来看，有证据表明：大型生产者能够与环境主管部门协商环境收费，而小型生产者则无法。也有证据表明：这种商定的环境费用可能低于未协商的费用。例如，散装废物产生者的单位废物处理费要比其他废物产生者低。如果废物的边际损害成本在增加，这种收费结构在社会上并不有效，但它们却很普遍。在这里展示的是它们既可以增加总排放量，又可以减少竞争。

此外，本研究也存在一定局限性，即企业生产相同的商品，可以进一步拓展研究差异化产品的情况-替代品或者互补品；在该情况下，还可细化考虑动态的Stackelberg竞争以及这种竞争中排放费用的影响等。