考虑商品数量和商品拣选成本的AGV智能仓库订单分批问题研究
2022-02-08张国维吴凌云
张国维, 吴凌云
(1.中国科学院 数学与系统科学研究院 应用数学研究所,管理、决策与信息系统重点实验室,北京 100190; 2.中国科学院大学 数学科学学院,北京 100049)
0 引言
近年来,随着电子商务的快速发展,电商物流面临的压力越来越大[1]。传统仓库采用“人到货”的拣选模式,拣选工人需要在仓库中来回往返穿梭,对体能的消耗比较大,拣选效率也不高。AGV(Automated Guided Vehicle,自动导引车)智能仓库是一种基于“货到人”拣选模式的自动化仓库,通过AGV将货架搬运至拣选工作站,再由拣选工人从货架上拣选商品来完成订单的拣选工作[2]。这种“货到人”拣选模式可以减少拣选过程中不必要的体能支出,提高订单拣选效率。
图1所示为AGV智能仓库的示意图[3]。当一个订单分配给一个拣选工作站时,空闲的AGV会将满足该订单的货架从储位搬运到相应的拣选工作站,排队等待拣选工人的拣选。当一个货架拣选完成后,AGV会将该货架搬运至一个空闲的储位。当一个订单拣选完成后,该订单可以从拣选工作站释放,一个新订单可以继续分配给该拣选工作站。一个拣选工作站往往设置多个订单槽位,使得一个拣选工作站可以同时处理多个订单[4]。因此,将合适的订单集合成批次订单同时进行处理,可以极大地降低拣选成本,提高拣选效率。
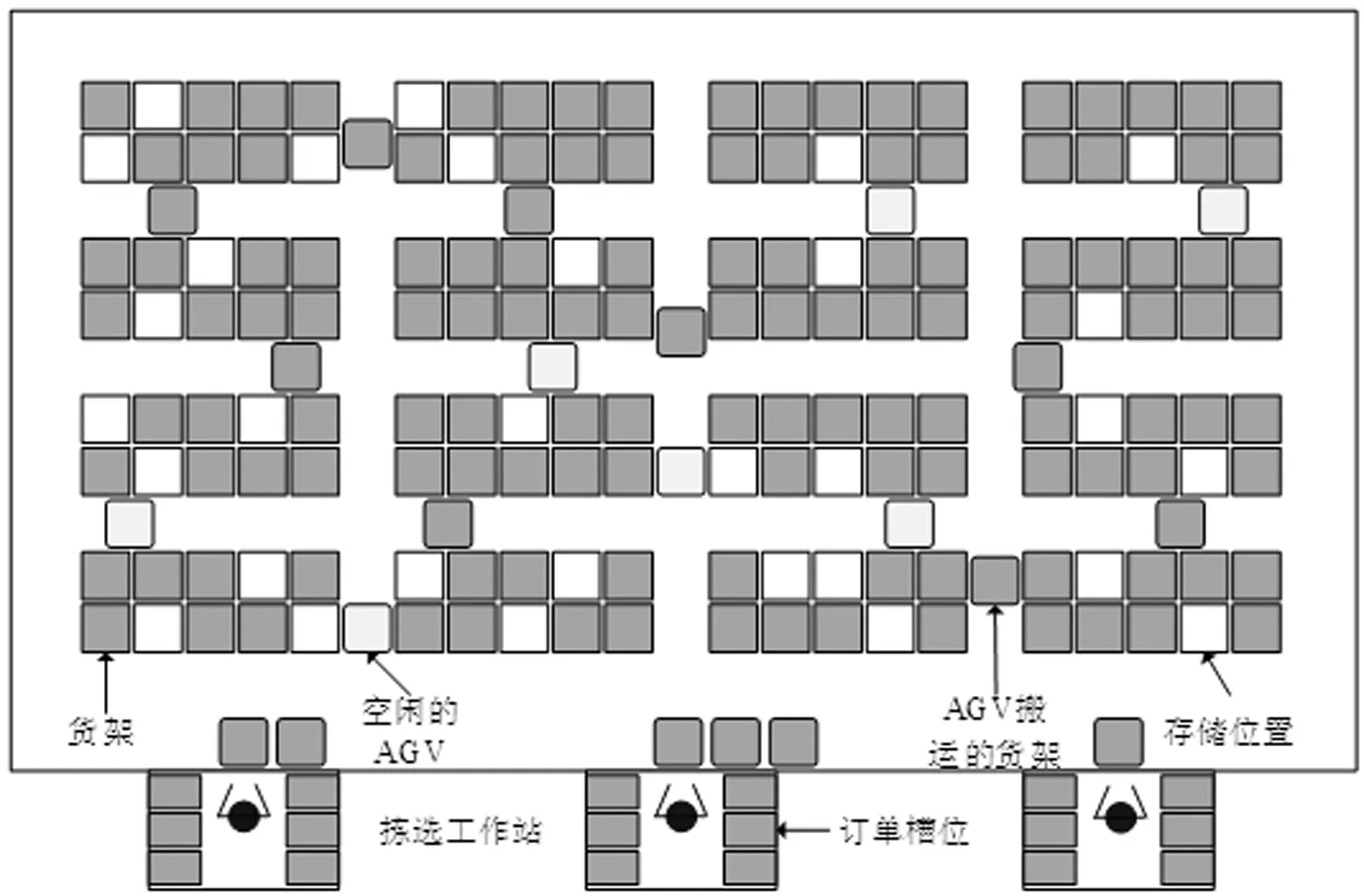
图1 AGV智能仓库示意图
传统仓库订单分批问题的研究已经比较丰富[5~7]。但这些研究成果很难直接应用到AGV智能仓库的订单分批问题中。目前,针对AGV智能仓库订单分批问题的研究还比较少。Xiang等建立了以最小化货架搬运次数为目标的整数规划模型,基于最大化订单相似性得到订单分批问题的初始解,并利用变邻域搜索算法对初始解进行改进[8]。李珍萍等以最小化货架搬运成本和商品拣选成本为目标,建立了AGV智能仓库订单分批问题的整数规划模型,并基于加权相似度设计了贪婪求解算法[9]。以上研究一般是基于静态批次的假定,即一个批次包含的订单全部释放才能分配新的订单。此外,也有一些学者在动态批次的假定下对订单分批问题进行研究。Boysen等将动态分批问题建模为一个排序问题,通过交替求解订单排序和货架排序问题来确定订单拣选的顺序和货架访问拣选工作站的顺序[4]。但实际应用中往往很难保证货架按照确定的顺序到达拣选工作站,因此,该模型的实用性受到很大限制。Xie等从在线优化的角度进行建模,根据拣选工作站正在拣选的订单和已经搬运的货架信息来确定将哪些订单分配到拣选工作站[10]。但该模型是从局部对订单分批进行优化,缺乏对全局的把控。
此外,以上的研究中还存在两方面的不足。首先,已有研究一般假设货架上商品的存储数量是充足的。但在实际应用中,货架上商品的存储量是有限的。其次,已有研究中一般将货架搬运次数作为目标函数。但是拣选工人从货架上拣选商品的成本也是很重要的一部分成本。针对已有研究中的不足,本文将研究考虑商品数量和商品拣选成本的AGV智能仓库订单分批问题,建立订单分批问题的数学模型,分析订单分批问题的结构和特点,并提出快速高效的求解算法。
1 问题描述
已知仓库中每个货架上存储的商品种类和数量,待拣选订单中包含的商品种类和数量,拣选工作站的容量(同时拣选的订单数量的上限)。AGV智能仓库订单分批问题是将给定的待拣选订单组成不同的批次,使得每个批次包含的订单数量不超过拣选工作站的容量,并为每个批次选择需要搬运的货架,使得完成订单拣选的总成本最小。
订单拣选的成本主要包括两方面: AGV搬运货架的成本和拣选工人从货架上拣选商品的成本。由于AGV智能仓库中货架的位置是实时变动的,货架的移动距离不能够准确地衡量[11,12]。为了简化问题,我们假设每个货架搬运一次的成本是固定的,因此,我们利用线性模型来建模货架搬运成本。拣选工人从一个货架上拣选两件相同的商品比拣选两件不同的商品的效率更高(拣选工人拣选商品的成本存在规模经济),因此,我们利用固定成本和变动成本来建模拣选工人从货架上拣选商品的成本。
2 模型构建
为了建立AGV智能仓库订单分批问题的数学模型,我们定义如下符号。
(1)索引
i:商品索引,i∈I;p:货架索引,p∈P;o:订单索引,o∈O;b:批次索引,b∈B。
(2)参数
c1:搬运一次货架的成本;c2:从货架上拣选一种商品的固定成本;c3:从货架上拣选一件商品的变动成本;C:拣选工作站的容量;Dio:订单o中商品i的需求量;Sip:货架p中商品i的存储量。
(3)决策变量
wob:0-1变量,订单o是否被分配到批次b;xpb:0-1变量,批次b是否需要搬运货架p;yipb:0-1变量,批次b是否需要从货架p上拣选商品i;zipb:批次b需要从货架p上拣选商品i的数量。
根据以上符号,可以将订单分批问题表示为一个整数规划模型。
(1)
(11)
目标函数(1)表示极小化订单拣选的总成本,其中第一项表示货架搬运成本,第二项表示商品拣选的固定成本,第三项表示商品拣选的变动成本;约束条件(2)表示每个订单恰好被分配到一个批次中;约束条件(3)表示分配到每个批次的订单数量不超过拣选工作站的容量;约束条件(4)和(5)表示每个批次只能从选中的货架上拣选商品;约束条件(6)表示每个批次中每种商品的拣选量恰好等于该批次所有订单中该商品的需求总量;约束条件(7)表示每个货架上每种商品的拣选量不超过该货架上该商品的存储量;约束条件(8)~(11)表示决策变量的取值范围。
(12)
在下文中,我们使用目标函数(12)作为订单分批模型的目标函数。
3 求解算法
求解AGV智能仓库订单分批问题需要解决两个相互关联的决策问题:决定每个批次包含哪些订单(批次组合问题),决定每个批次需要搬运哪些货架(货架选择问题)。已有的研究中通常将这两个决策问题分开求解:先求解批次组合问题,再求解货架选择问题[8,9]。已有文献一般通过订单的相似性作为组合批次的指标,但是,订单相似性并不能直接反映拣选该批次需要的拣选成本。而在求解货架选择问题时,由于批次已经确定,批次使用的货架信息并不能反馈到批次组合问题来做出更好的决策。
本文针对订单分批问题的特点,提出了一种基于订单和货架交替选择的贪婪求解算法。通过交替确定每个批次中包含的订单和需要使用的货架,货架选择的信息可以及时得到反馈,从而在当前批次后续订单选择中做出更好的决策。
该算法的具体步骤如下:
Step1初始化当前批次b=1,已分批订单数量n=0。
Step2如果n=|O|,转到Step 10。如果n<|O|,从未分批的订单中选择一个包含商品种类最多的订单加入到当前批次,记录当前批次剩余空间k=C-1,令n=n+1。
Step3选出可以满足当前批次中未满足商品种类最多的货架。如果可选的货架数量大于一个,则从中随机选出一个包含未分批订单中商品种类最多的货架。将选择的货架加入到当前批次,并更新货架上商品的剩余数量和当前批次中未满足的商品数量。
Step4重复Step 3直到当前批次中的商品全部被满足。
Step5从未分批的订单中选出所有能够由当前批次已选择的货架满足的订单。如果可选订单数量为零,转到Step 7。 如果可选的订单数量大于一个,则从中选出包含商品种类最多的订单。如果可选的订单数量还大于一个,则从中选出随机选出一个与已加入当前批次的订单包含相同商品种类最多的订单。将选择的订单加入到当前批次,并更新货架上商品的剩余数量,令k=k-1,n=n+1。
Step6重复Step 5直到没有未分批的订单能够由当前批次已选择的货架满足或当前批次包含的订单数量等于拣选工作站的容量C。
Step7以概率(1-e-k)判定是否继续向当前批次加入新订单。如果继续加入新订单,则转到Step 8;否则,转到Step 9。
Step8从未分批的订单中选出所有能够由已选择的货架满足至少一种商品的订单。如果可选的订单数量为零,转到Step 9。 如果可选的订单数量大于一个,则从中选出可以由已选择的货架满足商品种类最多的订单。如果可选的订单数量还大于一个,则从中选出随机选出一个与已加入当前批次的订单包含相同商品种类最多的订单。令k=k-1,n=n+1,转到Step 3。
Step9结束当前批次,并记录当前批次包含的订单,需要搬运的货架及从每个货架上拣选商品的种类和数量,令b=b+1,转到Step 2。
Step10结束计算,输出每一个批次包含的订单,需要搬运的货架及从每个货架上拣选商品的种类和数量。
4 算例分析
4.1 算例模拟和参数设置
算例模拟主要包含两个步骤:货架模拟和订单模拟。货架模拟确定每个货架上存储的商品种类和数量,订单模拟确定每个订单包含的商品种类和数量[3,10]。货架模拟:每个货架包含8个货位,每个货位可以存储一种商品。每种商品在一个货架上的存储量为区间[1,20]的一个随机整数。每个货架上存储的商品从所有商品中随机选择。订单模拟:商品的需求频率服从参数为2/|I|的几何分布。包含一种,两种,三种商品的订单的概率分别为0.5,0.25和0.25。订单中每一种商品的需求量为1或2,概率分别为0.9和0.1。
根据商品种类数量,货架数量和订单数量的不同,我们将模拟算例设置为小规模,中规模和大规模三种不同规模。不同规模算例的参数设置如表1所示。
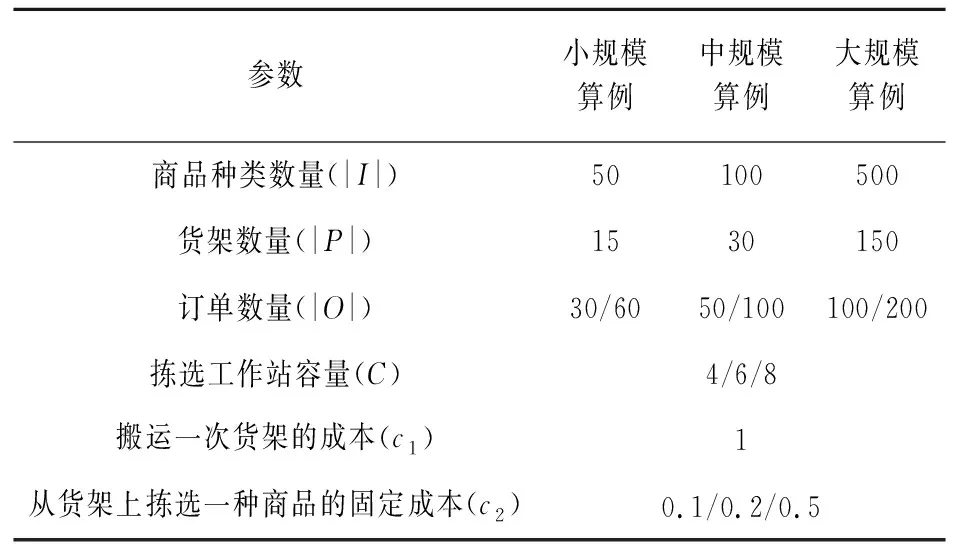
表1 不同规模算例的参数设置
4.2 算例结果
为了验证本文提出的贪婪算法的有效性,分别将该算法与CPLEX求解器和文献[9]中提出的基于相似性的分批算法进行对比,分析其求解质量和求解速度。文献[9]中的订单分批模型中并未考虑商品数量,因此,我们利用本文提出的贪婪算法的Step 3和Step 4为每个批次选择相应的货架。此外,根据文献[9]的结论,我们将基于商品的订单相似度的权重设置为c2/(c1+c2),将基于货架的订单相似度的权重设置为c1/(c1+c2)。
本文的算法是利用Python进行编程,在AMD R5-3600处理器的Windows电脑上运行的。本文使用CPLEX V12.10,设置最大运行时间设置为600秒。本文提出的贪婪算法和基于相似性的分批算法分别运行100次,取100次中得到的最好的解,以下结果展示中均为算法运行100次的总时间。
对于小规模算例,我们分别采用CPLEX求解器、基于相似性的分批算法和本文提出的贪婪算法进行求解。求解结果如表2所示。对于CPLEX求解器,我们展示了求解结果和运算时间;对于基于相似性的分批算法,我们还展示了该算法求解结果相对于CPLEX求解结果的误差百分比;对于本文提出的贪婪算法,我们也展示了该算法相对于基于相似性的分批算法的求解结果下降百分比。
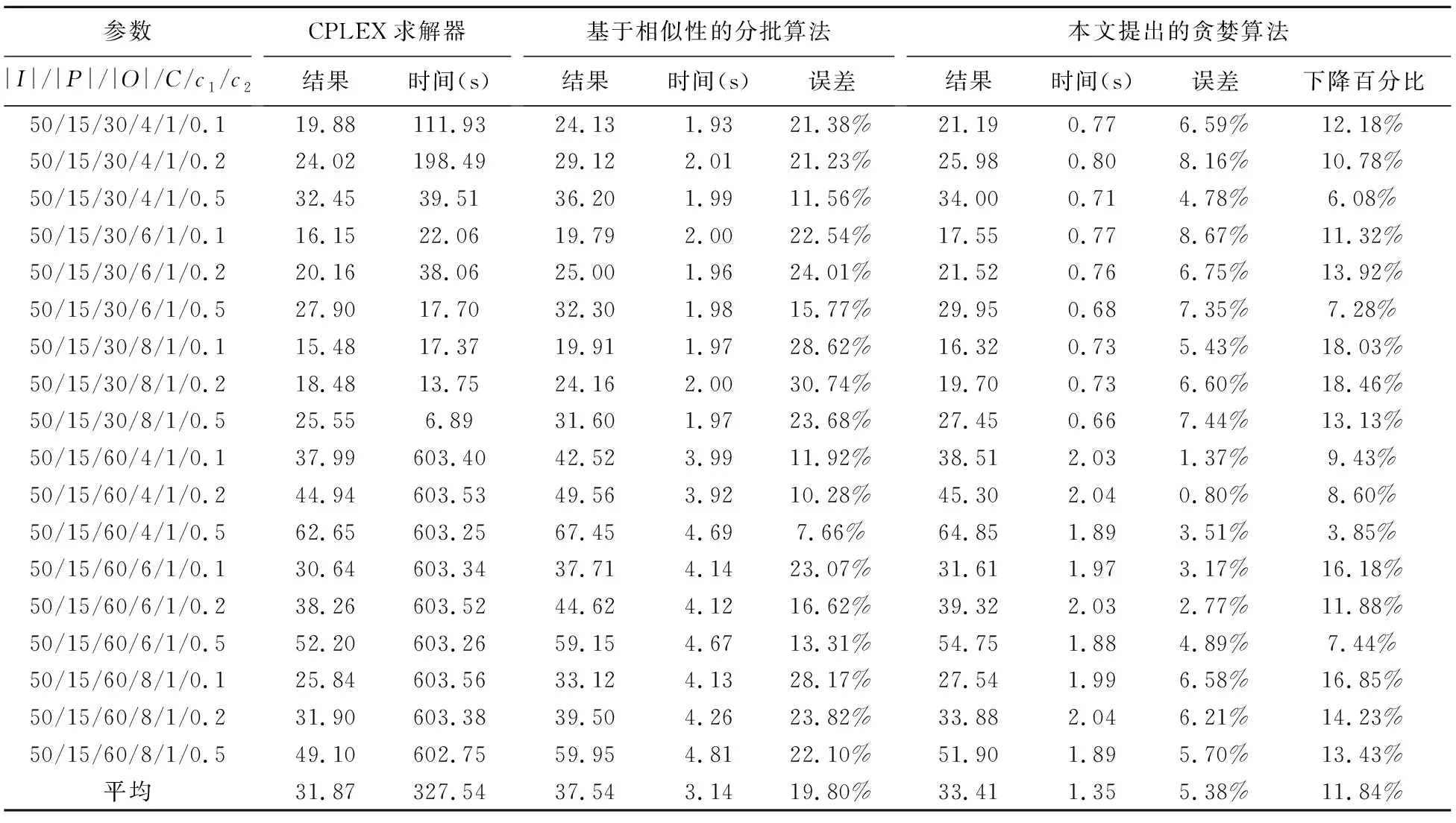
表2 小规模算例的求解结果
根据表2可知,对于小规模算例,当订单数量为30的时候,CPLEX可以得到精确最优解,而当订单数量为60的时候,CPLEX在设置的最大运行时间内无法得到精确最优解。相对于CPLEX的求解时间,基于相似性的分批算法和本文提出的贪婪算法具有明显的优势:基于相似性的分批算法的平均运算时间为3.14秒,本文提出的贪婪算法的平均运算时间为1.35秒。由于基于相似性的贪婪算法需要计算任意两个订单之间的相似性,因此,该算法的计算复杂度较高,运算时间也比本文提出的贪婪算法要长。相对于CPLEX的求解结果,基于相似性的分批算法的误差百分比基本都在10%以上,平均误差百分比为19.8%;而本文提出的贪婪算法的误差百分比均不超过10%,平均误差百分比为5.38%。相对于基于相似性的分批算法,本文提出的贪婪算法的平均下降百分比约为11.84%。
对于中规模和大规模算例,我们采用基于相似性的分批算法和本文提出的贪婪算法进行求解。求解结果如表3和表4所示。
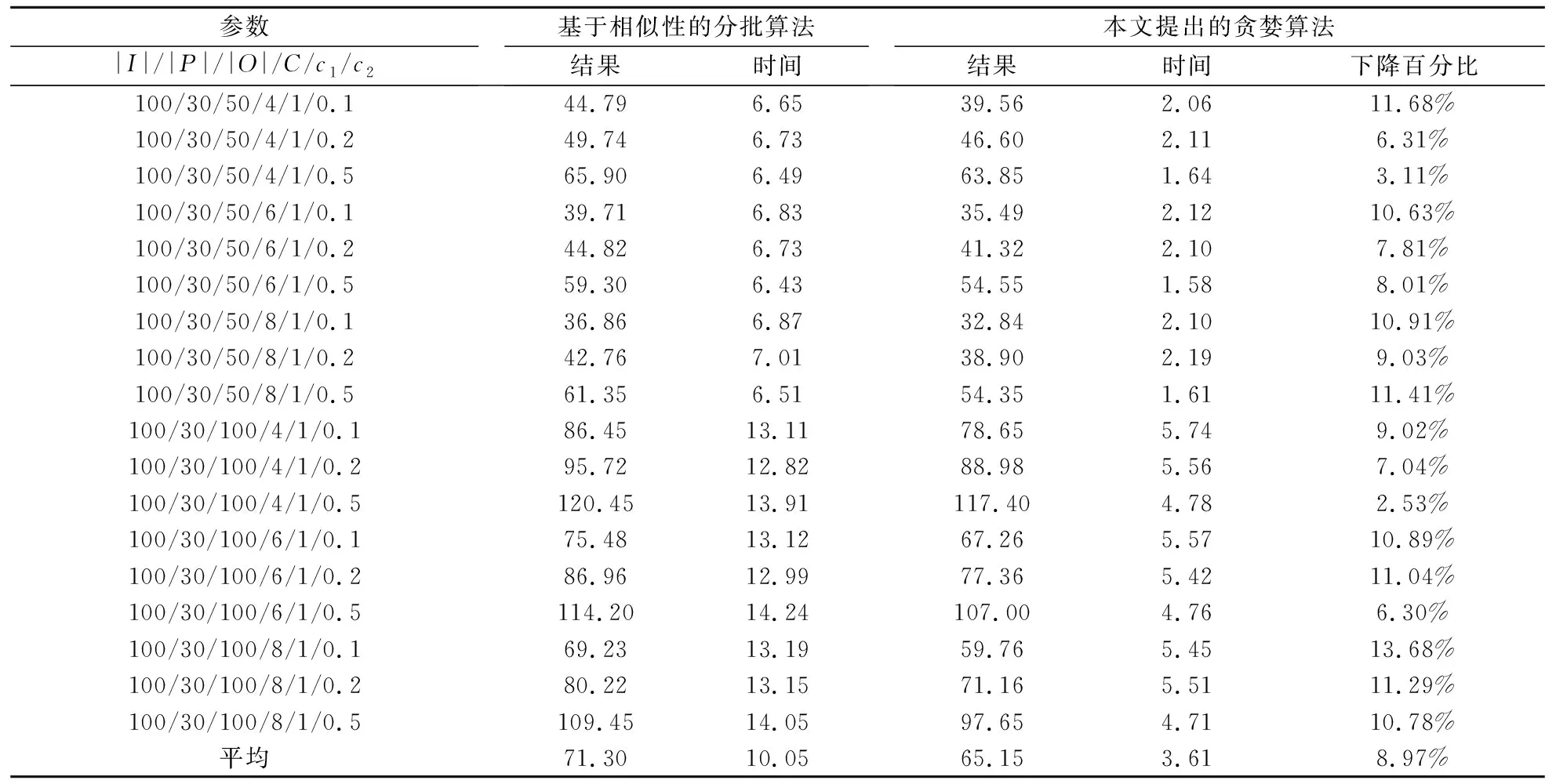
表3 中规模算例的求解结果
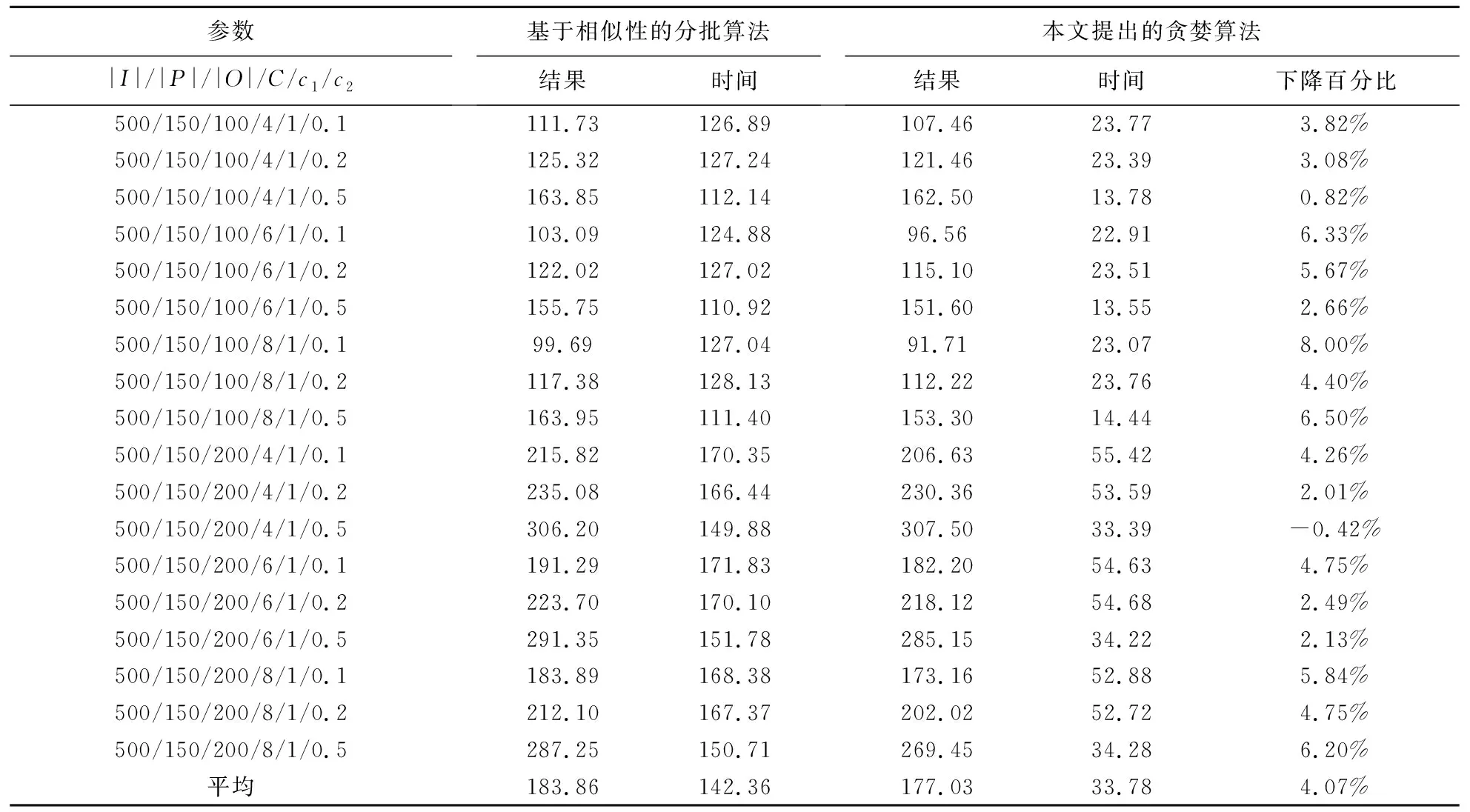
表4 大规模算例的求解结果
根据表3和表4可知,随着问题规模的增加,基于相似性的分批算法和本文提出的贪婪算法的运算时间有所增加,尤其是基于相似性的分批算法,求解大规模算例的运算时间都超过了100秒。相比于基于相似性的分批算法,本文提出的贪婪算法在运算时间上仍然有较大的优势。在本文中,两个算法的运算时间为运行100次的时间,但是在实际应用中,可以调整算法运行的次数来平衡算法的运算时间和求解质量。此外,本文提出的贪婪算法可以在不同的CPU核心、不同的机器上并行运算,因此,算法的运行次数可以更加灵活地进行调整。
对于中规模和大规模算例,本文提出的贪婪算法的求解结果相对于基于相似性的分批算法下降的百分比的平均值分别为8.97%和4.07%,与小规模算例的结果相比有所下降。我们认为产生这种现象的主要原因是随着商品种类的增加,算例模拟时可以产生的订单商品组合呈指数级增长,而算例模拟的订单数量并没有大幅度增加,因此,订单之间的差异较大,通过订单分批来提高拣选效率的能力降低。在实际应用中,虽然仓库中的商品种类很多,但实际的订单种类是远远小于商品种类的组合数,因此,本文提出的贪婪算法在实际应用中的效果会更好。
此外,我们还发现,当c2取值较小时,下降百分比相对较大;而当c2取值较大时,下降百分比相对较小。产生这种情况的主要原因是随着c2取值的增加,商品拣选成本在总成本中的比重增加。本文提出的贪婪算法认为减少货架搬运次数的优先级高于减少商品拣选次数的优先级,不会因为c2取值的不同而改变;而基于相似性的贪婪算法中的订单相似度会根据取值的不同而改变,能够在一定程度上对货架搬运成本和商品拣选成本进行权衡。因此,在c2取值较大时,本文提出的贪婪算法的优势会相对降低。但是在实际应用中,c2往往是远大于c1的,因此,本文提出的贪婪算法在实际应用中会有更好的效果。
4.3 考虑商品拣选成本的有效性
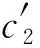
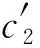
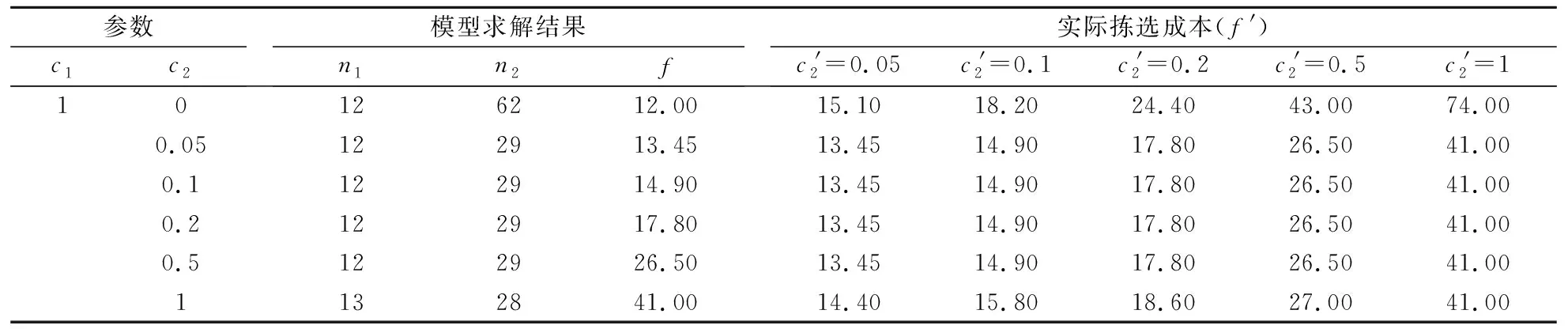
表5 不同商品拣选固定成本下小规模算例的模型求解结果和实际拣选成本
5 结论
订单分批问题是基于“货到人”拣选模式的AGV智能仓库订单拣选过程中一个关键的决策问题,对订单拣选效率有极大的影响。本文研究了考虑商品数量和商品拣选成本的AGV智能仓库订单分批问题,建立了以极小化货架搬运成本和商品拣选成本为目标的整数规划模型,并设计了快速高效的贪婪求解算法。本文提出的模型考虑了商品数量和商品拣选成本,相比于已有研究中的订单分批模型更符合实际情况,增加了模型的实用性。针对订单分批问题的结构和特点,本文提出了一种基于订单和货架交替选择的贪婪求解算法。通过订单和货架的交替选择,可以做出更合理的决策,从而达到更好的求解效果。通过不同规模的算例对本文提出的贪婪算法进行了分析,结果表明,相对于CPLEX求解器,本文提出的贪婪算法求解结果的误差百分比约为5.38%,相对于基于相似性的分批算法,本文提出的贪婪算法在运算时间和解的质量上都有明显的优势。对比不考虑商品拣选成本的订单分批模型,本文提出的模型可以大幅度降低商品的拣选次数。此外,即使实际中商品拣选的固定成本相对于货架搬运成本小很多时,仍然不能忽略商品拣选成本。
在实际应用中,AGV智能仓库包含多个不同的拣选工作站,如何有效地将这些批次分配到不同的拣选工作站,有待未来进一步的研究。此外,如何确定批次的拣选顺序,也是未来的一个重要研究方向。
