脉冲荷载激励下扣件弹条扣压力检测方法

2022-02-07曹子文丁正祥柳明佳施新荣刘林芽宋瑞

铁道建筑 2022年12期

曹子文丁正祥柳明佳施新荣刘林芽宋瑞

1.华东交通大学交通运输工程学院，南昌 330013；2.浙江省交通工程管理中心，杭州 311215；3.中铁二十四局集团浙江工程有限公司，杭州 310009；4.南昌工程学院，南昌 330099

扣件系统是高速铁路轨道结构的重要组成部分，主要功能是为钢轨提供足够的扣压力，防止钢轨发生横向、纵向移动，为列车运营的舒适性和安全性提供保障。在实际服役条件下，扣件系统面对的环境复杂多变且需要承受大量的外部荷载，容易出现弹条松脱、损伤和失效的现象［1-2］。这时扣件弹条的扣压力往往不能满足相关规范要求，并且相比于扣件缺失和断裂，扣压力不足的情况在线路养护中不易被发现。一个扣件弹条的扣压力不足会诱发周围扣件松脱，加剧轨道结构破坏，影响列车的安全平稳运行，甚至会导致脱轨事故［3-4］。因此，对扣件弹条扣压力的检测至关重要。

余喆琦等［5］为了提高铁路扣件压力检测的自动化程度，弥补人工检测精度低、效率低等方面的不足，研发了一种基于激光测量原理的扣件弹条扣压力自动检测系统，该系统使用激光测量代替塞尺进行读数。Lorente等［6］通过线结构光传感器获取扣件系统的三维点云，提出了一种基于三维ICP（Iterative Closest Point）匹配的扣件检测方法，用来识别扣件的缺失和损失。高玉和、张松琦等［7-8］利用夹具夹住扣件，采用机械方式将扣件提起，在扣件刚开始脱离钢轨轨面时通过测力传感器直接测试扣件弹条的扣压力，实现对扣件弹条扣压力在线检测。TB/ T 3396.2—2015《高速铁路扣件系统试验方法第2 部分：组装扣压力的测定》中提出一种弹条扣压力的测定装置，采用液压千斤顶加载，四连杆夹具夹紧弹条，当手动加载至弹条完全脱离绝缘轨距块并且用0.1 mm 的塞尺正好能塞进弹条和绝缘轨距块的间隙时，读取测力表得到扣压力。上述扣件弹条扣压力测试方法中，激光测量可以提高检测的效率，却不能得出较为准确的扣压力；直接通过提升弹条的方式能测出比较精准的扣压力，但是安装及操作复杂，效率低且不能满足无损、高效的检测要求。为了满足对铁路线路中扣件系统扣压力的检测需求，亟待研发一种快速、无损的检测方法。

本文以高速铁路中WJ⁃7型扣件弹条为例，对扣件系统进行脉冲荷载激励试验，根据弹条在不同扣压力状态下的固有振动特性，得到扣件弹条扣压力与弹条频率的对应关系；通过脉冲激励扣件弹条得到其模态频率，间接推算扣压力。

1 模态分析理论

结构的模态分析即对其振动响应进行分析，可研究结构自身的固有频率、振型等模态参数。根据结构振动理论建立的扣件系统动力学方程为

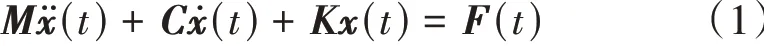
由于大多数结构的阻尼较小，对模态参数影响不大，在工程上基本可忽略，因此研究弹条的振动特性时不考虑结构阻尼。实际工作中，弹条承受螺栓预紧力产生的预应力会改变弹条自身的刚度，可能会影响弹条的固有频率，因此对弹条进行模态分析时要考虑预应力的影响［9］。弹条预应力计算式为

式中：Kf为预应力产生的附加刚度矩阵。

因此，可得无阻尼的弹条振动方程为

2 扣压力检测试验

2.1 螺栓扭矩与扣压力的关系

高速铁路WJ⁃7 型扣件由T 形螺栓、钢轨、弹条等部件组成，通过螺母与T 形螺栓之间的紧固扭矩让平垫圈向下移动产生垂向的预紧力，为弹条提供扣压力。根据扣件的结构特性及受力分析可以间接得出弹条扣压力［10］。螺栓预紧力F与紧固扭矩T的关系为［11］

式中：k为扭紧力矩系数，取0.2～0.3；d为螺栓公称直径，mm；

根据扣件弹条等效受力情况（图1），可以得出弹条扣压力N与螺栓预紧力F的关系为［10］

图1 扣件弹条等效受力示意

式中：L1为弹条后肢圆心到螺栓圆心的距离，mm；L0为弹条后肢圆心到前肢圆心的距离，mm。

根据WJ⁃7 扣件系统的规格，取d=24 mm，k=0.2，L1=35 mm，L0=86 mm。根据式（4）和式（5）可以计算得到不同紧固扭矩下的扣压力，见表1。

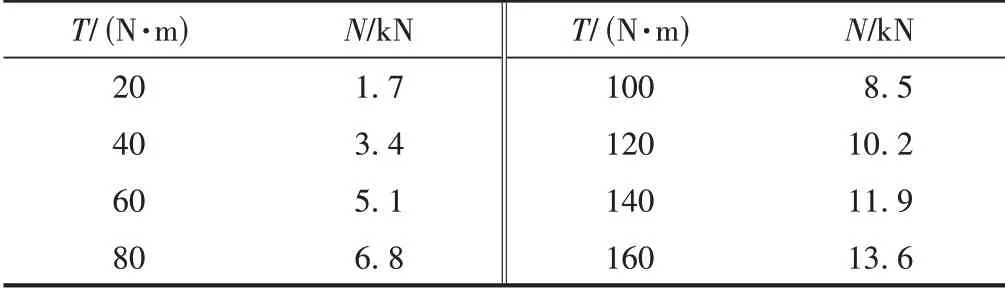
表1 不同紧固扭矩对应的弹条扣压力

2.2 脉冲荷载激励试验

为了研究扣件弹条在不同扣压力状态下的模态特征，在华东交通大学轨道试验基地的高速铁路线路上进行模态试验。该线路采用CRTSⅠ型板式无砟轨道、60 kg/m 钢轨、WJ⁃7 型扣件系统以及W1 型弹条。高速铁路扣件弹条的前两阶振动频率大多数在400～1 200 Hz［12-13］，因此选择弹条频率0～1 200 Hz 进行研究。

为了获取弹条模态特征，对WJ⁃7型扣件弹条进行脉冲荷载激励试验。考虑到室外环境、测试便捷等因素，拾振器采用PCB352C04 振动加速度传感器，频响范围1～10 000 Hz；激励系统使用型号ICP9312 的力锤，灵敏度为0.997 mV/N；数据采集装置选择比利时LMS310系统，设置采样频率4 096 Hz。由于弹条结构的复杂性，单个激励点不能采集到准确的模态参数，在其表面布置27个激励点；为避免加速度传感器的质量对测试结果造成影响，布置1 个传感器作为响应点（7号点），如图2所示。测试时用力锤依次敲击每个激励点3次，锤击的力度和方向尽量保持一致，且每次调整不同扣压力工况测试时传感器的安装位置不变。

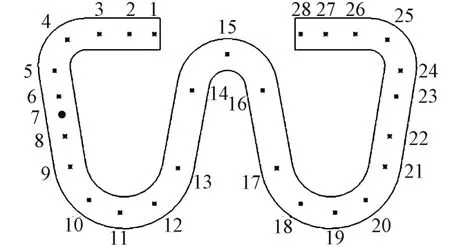
图2 模态测试激励点及传感器布置

2.3 试验结果及分析

2.3.1 标准扣压力状态下的模态分析

对WJ⁃7 型扣件调整到标准的安装扣压力状态下进行模态测试。根据科技基〔2007〕207 号《WJ⁃7 型扣件暂行技术条件》中的“WJ⁃7 型扣件组装暂行技术标准”可知，W1 型扣件弹条单个扣压力大于9 kN，对应的安装扭矩约120 N·m。把螺栓扭矩调整到120 N·m时，计算得到的扣压力约10.17 kN（参见表1），满足标准安装要求。

试验时，先用数值扭矩扳手将待测扣件的螺栓扭矩调整到120 N·m，再将速度传感器粘贴在弹条上的7号测点处，最后用力锤依次激励测点，就可得到现场所有测点的频响函数汇总曲线，见图3（a）。可以看出，标准安装状态下的扣件弹条在0～1 200 Hz内共有两阶模态，不同激励点得到的加速度导纳值有差异，但固有频率相同。为了获取其准确的模态参数，采用LMS Test.Lab 中的PolyMAX 方法［14］对频响函数汇总曲线进行进一步处理，得到求和曲线，见图3（b）。两阶模态的振型见图4。

图3 频响函数曲线

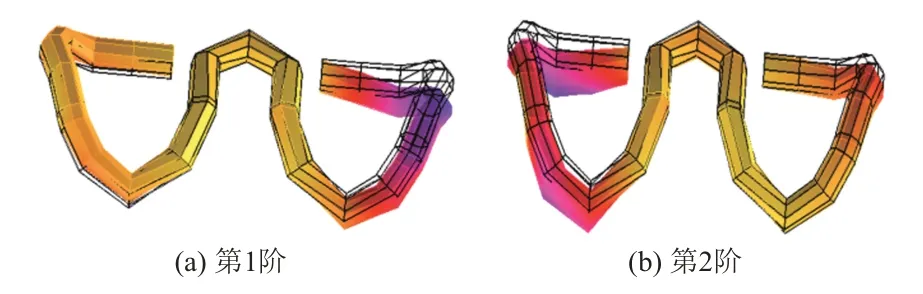
图4 标准扣压力状态下弹条振型

由图3、图4 可知：弹条的第1 阶固有频率为781.60 Hz，其振型为外端的两侧肢以扣压端和支承端为支点的垂向振动，两侧肢振动方向相反，后肢支撑端承受较大扭矩；第2 阶固有频率为922.86 Hz，其振型为外端两侧肢以扣压端和支承端为支点的垂向振动，且两侧肢振动方向相同。

2.3.2 不同扣压力状态下的模态分析

标准扣压力状态下弹条第2阶固有频率的加速度导纳峰值并不明显，因此分析不同扣压力状态对扣件弹条模态特征的影响时只分析其第1阶模态特征。按照表1 中的8 种扣压力工况依次进行测试，得到各工况下的第1 阶模态振型，见图5。可以看出：不同扣压力对应的第1 模态振型基本一致，都是两侧肢以扣压端和支承端为支点的垂向振动，振动方向相反；后肢支撑端承受较大扭矩，为损伤的敏感位置，且与现场发现的弹条断裂位置吻合。由此可见，扣压力对WJ⁃7型扣件弹条的第1 阶振型的影响不大，可能与其本身接触的边界条件有关。

图5 不同扣压力对应的第1阶实测模态振型

随着施加给扣件弹条的预紧力逐渐加大，改变了弹条的预应力，进而影响由预应力附加给弹条的刚度矩阵［10］。不同扣压力下的模态参数见表2。可知，随着扣压力增大，对应的第1阶固有频率也增大，但阻尼比无明显的变化规律。可见，预应力变大使弹条的刚度矩阵增加，从而影响了弹条的固有频率。

表2 不同扣压力下的模态参数

因此，根据扣压力N与第1 阶固有频率V的对应关系，对这两个参数进行线性拟合，拟合曲线见图6。可知，扣压力与弹条固有频率拟合曲线的相关系数为94%，能满足工程上对扣压力测试结果的需求。要获取扣件系统的扣压力，可先通过测试得到扣件弹条的固有频率，代入拟合曲线的关系式中，推算出待测扣件的扣压力。

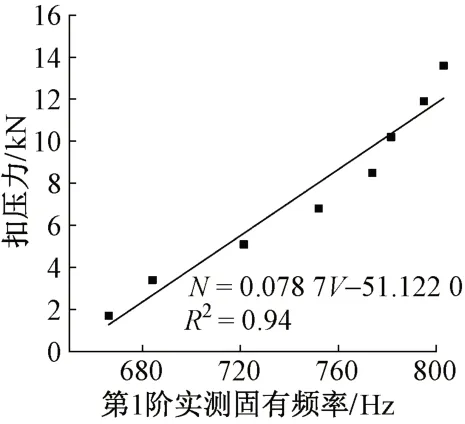
图6 扣压力与弹条固有频率的拟合曲线

3 弹条扣压力测试方法

由于WJ⁃7 型扣件弹条的侧肢在不同扣压力状态下的垂向振动均比较明显，且第1 阶模态节点不在弹条侧肢上，因此将加速度传感器安装在侧肢的7 号点位置是可行的。根据频响函数汇总曲线可知，激励点的不同不会影响第1 阶固有频率，但考虑到弹条空间结构的复杂性和尽量保证原点激励，力锤的敲击点选择靠近传感器的8 号点。对8 号点施加不同扣压力时的相干函数曲线见图7。可知，8号点的相干函数值接近于1，表明在该点激励满足试验要求。

图7 不同扣压力下8号点的相干函数曲线

因此，对工作状态的WJ⁃7型扣件弹条扣压力的检测可以通过在7 号点安装振动加速度传感器和敲击8号点，采集弹条的第1阶固有频率，再代入测试的扣压力与固有频率的关系曲线中，进一步得到相对应的扣压力。同理，对于其他弹条空间结构类似于WJ⁃7 型扣件的弹条，均可先研究其扣压力与固有频率对应的关系曲线，将得到的拟合曲线应用到扣压力检测中。