转子初始弯曲对航空发动机振动的影响
2022-02-06洪亮蒋云帆王艳丰贺延琛陈静张雄
洪亮,蒋云帆,王艳丰,贺延琛,陈静,张雄
(1.南京航空航天大学能源与动力学院,南京 210016;2.中国航发四川燃气涡轮研究院,成都 610500;3.西华大学航空航天学院,成都 610039)
0 引言
现代航空发动机追求高性能、高推重比,结构日趋复杂,工作条件越发苛刻,导致整机振动超限而影响发动机使用及试验的事故逐步增多[1]。控制发动机在工作过程中的振动水平对于提高发动机使用安全性、可靠性、寿命有着重要意义[2]。发动机振动控制需要多方面共同保证,其中转动件的动不平衡是影响发动机试车时振动超限的主要原因之一[3-5],因此发动机试车前均需对转子进行严格平衡。但受限于平衡机的功率,目前对于中大型发动机转子仅能采取低速动平衡的方法。低速动平衡在降低由于偏心离心力引起的振动或作用在轴承上、与工作转速频率相一致的振动中已被广泛应用。除动平衡外,转子的弯曲程度也是振动控制的重要一环。目前对于弯曲程度的控制主要采用转子跳动检查来保证。当转子跳动无法保证时,具有初始弯曲的转子能否通过动平衡修正。若能通过修正,修正后的弯曲转子是否会对整机振动产生影响需要开展研究。
对于具有初始弯曲转子的动平衡,国内外相关学者开展了一定的研究。Lees等[6-7]、Edwards等[8-9]、Pennacchi等[10]进行了一系列针对弯曲转子的模态识别和动平衡研究,完成了带初始弯曲转子在亚临界工作条件下的振动特性分析,开展了振动特性识别。通过振动信号的分析,实现了某些特定条件下亚临界弯曲转子的振动故障监控与诊断;张荣佩等[11]和何国安等[12]介绍了汽轮机转子常见永久弯曲发生的原因,通过对转子弯曲状态评估,弯曲振型分解,动平衡方案的正反问题求解等3个步骤,利用现场动平衡方法成功实现了带轻微弯曲状态刚性转子的修复,实现了不更换转子的稳定运行;冯国全等[13]对具有初始弯曲的转子系统进行了振动响应特点分析,从转子动力学理论出发,建立了适合工程应用的多自由度分析模型,给出了分析方法,得到了初始弯曲与不平衡响应在转子振动响应方面的不同影响及差异。但是,对于具有初始弯曲的转子能否通过动平衡检测,通过平衡检测的弯曲转子能否在发动机全转速范围内可靠工作尚未开展相关理论分析及试验研究。
本文结合理论推导及试验验证,对某弯曲转子的相关振动特性进行了研究。
1 整机振动现象
在某型航空发动机某台份的首次整机地面台性能调试试验中,发动机振动特性与该型其余台份发动机的不一致。为便于分析,归纳如下:
(1)发动机在过高压激起的2阶及4阶临界时,鼠笼振动出现明显峰值(其高压基频曲线如图1所示),且峰值远大于其余台份,与其它正常台份过临界振动高压基频对比对比如图2所示。
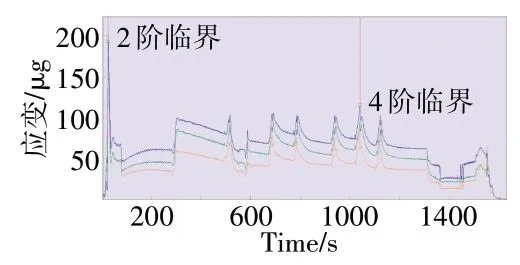
图1 鼠笼振动高压基频曲线
(2)发动机在各稳态下的基频振动水平均大于其余台份的,各测点稳态基频振动对比如图3所示。

图3 稳态基频振动对比
(3)涡轮测点出现了明显的发动机2倍频特征,且稳态时振动量级与基频相当,振动高压基频与2倍频对比见表1。瞬态时2倍频最大量级达到10.3g,超过基频,振动高压2倍频振动曲线如图4所示。

图4 振动高压2倍频曲线

表1 振动高压基频与2倍频对比 g
(4)除发动机基频及2倍频突出外,未见其余异常振动特征成分。
2 振动特性分析及检查结果
由于发动机在过高压2阶及4阶临界时出现了明显的振动反映,对发动机进行不平衡量的敏感性分析,分别在风扇、压气机、高压涡轮及低压涡轮4处施加相同不平衡量后提取各自在过2阶及4阶临界转速时的不平衡响应,有限元分析模型如图5所示,不平衡敏感性分析如图6所示。从图中可见,高压转子存在平衡状态不佳时易发生发动机过2阶及4阶临界转速时响应增大的可能。

图5 有限元分析模型

图6 不平衡敏感性分析
但该发动机的转子在试车前进行了动平衡,其中高压转子在高压压气机、高压涡轮单独平衡满足要求后还进行了组合动平衡,高压转子动平衡位置如图7所示,平衡结果见表2。从表中可见,高压转子不平衡量满足要求。因此转子初始静态不平衡量导致高压转子平衡状态不佳的可能性可以排除。
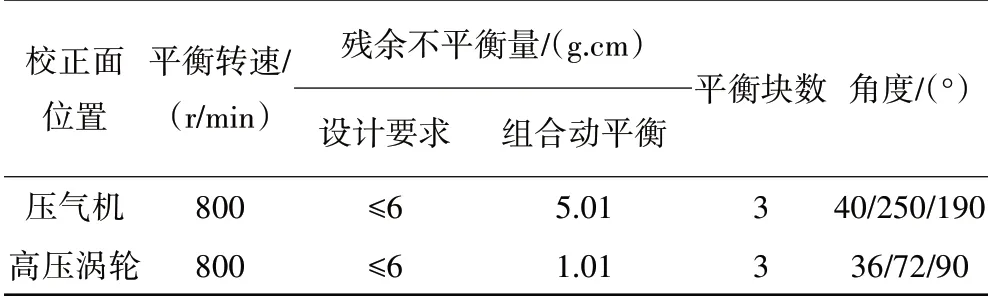
表2 组合动平衡最终残余不平衡量

图7 高压转子动平衡位置
除基频外,在发动机试验过程中还测到了明显的2倍频成分,通常认为2倍频与转子不对中密切相关[14-15],因此怀疑发动机高压转子的对中性不佳,并且目前的低速动平衡无法平衡转子初始弯曲的影响。
为验证高压转子对中性不佳的推测,试验后对发动机进行了分解检查,发现高压压气机转子后轴径向跳动超标。高压压气机转子后轴跳动检查位置如图8所示,检查结果见表3。从表中可见,高压压气机后轴呈弯曲状态,导致压气机及涡轮轴之间存在角度及平行不对中的情况。证明了振动分析的推测是正确的。

图8 高压压气机转子后轴跳动检查位置
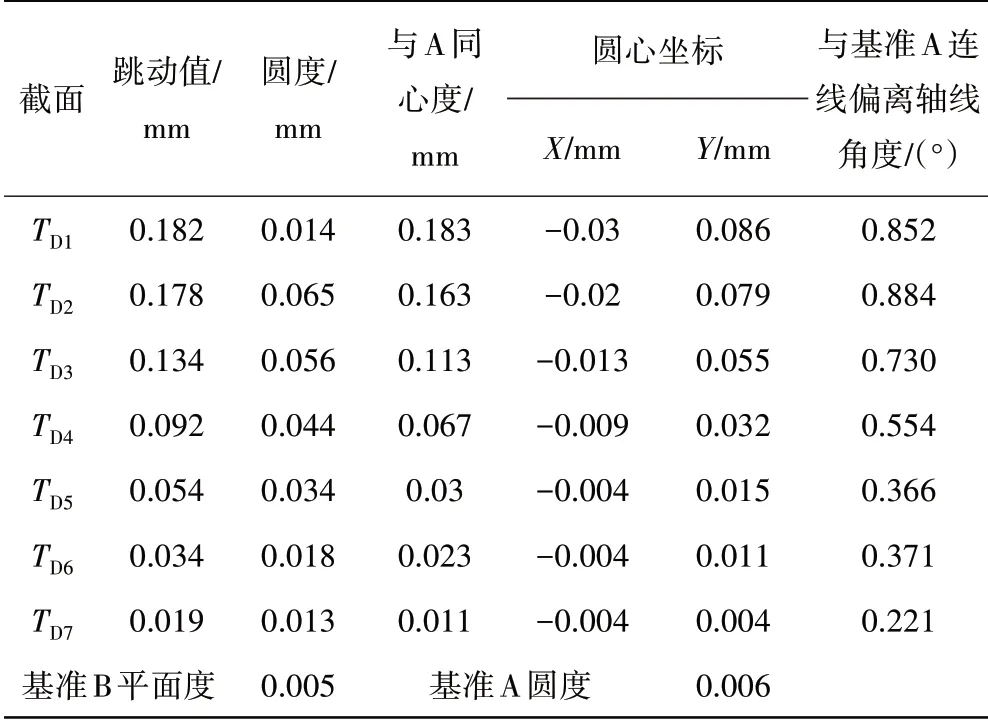
表3 跳动测量结果
同时,为分析低速动平衡与初始弯曲之间的关系,进行了如下理论推导。对带初始弯曲的Jeffcott转子(如图9所示)进行分析,转子的运动微分方程为
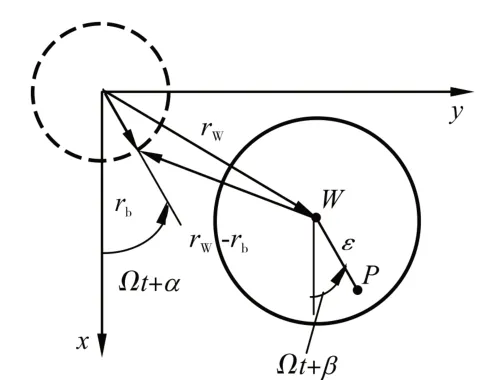
图9 带初始弯曲的Jeffcott转子

其中

式中:为圆盘质量偏心。

将式(2)、(3)代入式(1)并引入临界转速

则式(1)变为
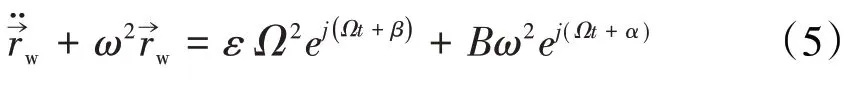
其解为

对式(6)的第2项进行如下变形

之后,就可将式(6)改写为

式中:第1项为轴弯曲引起的附加不平衡量与原始不平衡量迭加之后产生的不平衡响应;第2项则为轴的弯曲,其中初始弯曲B不随转速变化。
在转子上施加不平衡量u→,则转子的振动为
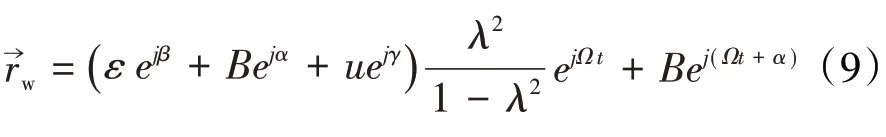
要使转子振动消除,则须有

该方程中包含有转速比λ,因此无法确定1个不平衡量u→,使得方程在任何转速比λ之下都成立。在平衡机上进行动平衡时,若取平衡条件为

式中:u为平衡校正量。
平衡之后,转子的运动中将保留轴的初始弯曲,即

此时,转子支座上的激振力得以消除

根据以上推导可见,当取式(11)为平衡条件时,可在所有转速下消除支座上的激振力。这就是低速动平衡机所采用的平衡原理。然而,由式(13)可知,当采用式(11)为平衡条件时,转子的初始弯曲不能太大。若初始弯曲偏大,由初始弯曲引起的不平衡响应会随着转速的升高而迅速增大,这会显著加剧转子自身的振动响应,给转子的安全稳定运转带来巨大的风险。
综上,动平衡不能使得转子初始弯曲的影响在所有的转速条件下得以消除,初始弯曲会在高转速时恶化转子的平衡状态加剧振动,因此必须严格控制转子的初始弯曲。
3 措施及效果
鉴于高压压气机后轴跳动超差严重,并引起了不可接受的整机振动水平,对后轴进行更换。更换符合要求的高压压气机后轴后,鼠笼振动高压基频曲线如图10所示,更换后轴前后高低压基频振动对比如图11所示。从图10中可见,更换后轴后发动机最大鼠笼基频约70 μɛ,恢复正常状态。机匣振动均大幅降低,也恢复正常状态。

图10 更换后轴后鼠笼振动高压基频曲线

图11 更换后轴后稳态基频振动对比
发动机在最大状态下的振动频谱如图12所示。从图中可见,更换后轴后,2倍频不再突出。
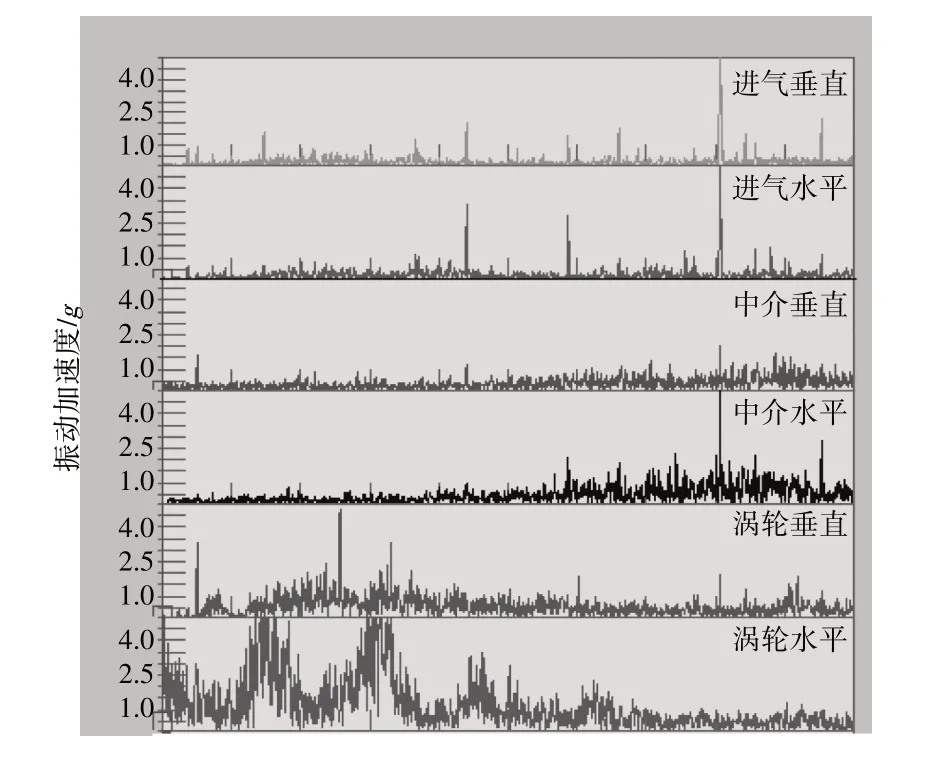
图12 发动机在最大状态下的振动频谱
4 结束语
对于具有初始弯曲的转子,可以通过调整质量块满足低速动平衡的检验要求。但在高转速下,初始弯曲会成为转子的附加不平衡量,影响转子的工作状态。因此对高速运转的转子,在仅进行低速动平衡时需要严格控制转子本身的弯曲量,避免工作时产生不可接受的振动。
