考虑残余顶推力作用时盾构下穿引起既有顶管管廊变形

2022-02-05章李刚楼佳悦冯国辉纪晓佳李毅李燚黄展军孔跃跃徐长节

科学技术与工程 2022年35期

章李刚，楼佳悦，冯国辉，纪晓佳，李毅，李燚，黄展军, 孔跃跃，徐长节,7,8*

(1.浙江华云电力工程设计咨询有限公司，杭州 310014; 2.浙江大学平衡建筑研究中心，杭州 310028； 3.浙江大学滨海和城市岩土工程研究中心，杭州 310058； 4.浙江安防职业技术学院应急技术学院，温州 325016； 5.南昌轨道交通集团有限公司，南昌 330013； 6.中铁十四局集团第四工程有限公司，济南 250002; 7.江西省地下空间技术开发工程研究中心，南昌 330013; 8.华东交通大学轨道交通基础设施性能监测与保障国家重点实验室，南昌 330013)

随着城市化进程的不断推进，城市地下空间的开发和利用已经成为专家学者关注的焦点。而城市地铁线路的建造难免会对邻近结构物产生不利影响，也会不可避免地下穿邻近既有管廊。盾构隧道的开挖建造会造成上覆既有管廊产生纵向不均匀沉降、破裂破损甚至存在渗水漏水的情况。对于如何评估隧道开挖对上覆既有管廊变形的影响是岩土工程界急需解决的难题。

理论解析的方法简单实用、耗能更小，可以用来初步评估邻近建筑物在隧道开挖下的变形响应。大部分土与结构相互作用解析方法采用两阶段法，第一阶段基于Loganathan等[1]提出的估算隧道开挖引起周围土体自由位移变化公式，将得到的自由土体位移转化成附加应力施加在既有邻近建筑物上，第二阶段用梁单元模拟邻近建筑物，土与结构之间相互作用采用相应的地基模型，结合两个阶段的结果获得其变形控制方程，最后解方程获得邻近建筑物变形响应应答。基于单参数地基模型，可文海等[2]将桩基简化成Euler-Bernoulli梁搁置在Winkler地基模型上，利用函数叠加法获得隧道开挖引起邻近群桩竖向位移解析解；梁荣柱等[3-4]用Euler-Bernoulli梁和Timoshenko梁模拟隧道单元，并将梁体搁置在Winkler地基模型上，分别获得下穿隧道引起上覆隧道变形解析解和简化计算方法。由于Winkler地基模型缺乏考虑土与结构相互作用中土体剪切影响，使得解析理论结果不够理想。为了克服这一缺点，Pasternak、Vlasov、Kerr地基模型由于能够考虑土体剪切效应被广泛应用于地下结构的研究中。基于双参数地基模型，管凌霄等[5]将既有管线简化成Timoshenko梁放置在Pasternak地基模型上，通过两阶段法获得既有管线在下穿隧道作用下的竖向变形响应；冯国辉等[6]基于Winkler和Pasternak地基模型研究了隔离桩对盾构掘进引起近邻高铁桩基水平变形的保护效果；何小龙等[7]、徐长节等[8]基于Pasternak地基模型分别研究了基坑开挖和单井降水对邻近管线变形的影响；Liang等[9]考虑到管-土分离的情况，采用Pasternak地基模型获得基坑开挖引起下卧隧道变形解析；Liang等[10]引入非线性Pasternak地基模型，利用牛顿迭代法获得了非线性土体下上覆隧道在盾构下穿作用下的简化计算方法。张世民等[11]基于土体非线性流变性和Pasternak地基模型获得双基坑开挖引起下卧既有隧道竖向受力变形计算方法，并通过与实测数据对比验证了计算方法的有效性；赵维等[12]基于Timoshenko梁和Pasternak地基模型获得基坑开挖引起下卧隧道隆起变形半解析解，并通过有限元方法验证了解析解的合理性；可文海等[13]、管凌霄等[14]基于Vlasov地基模型分别获得下穿隧道引起上覆管线竖向变形和水平位移解析解。同时也有不少学者指出Kerr地基模型也能精确的预测土与结构相互作用[15-18]。然而在现有的管廊研究中，大多数研究都是停留在有限元[19-20]和室内试验阶段[21-22]，鲜有理论部分研究[23]，基于此现展开对管廊在盾构下穿作用下的变形响应。

为了获得盾构下穿对上覆既有管廊变形的影响，结合既有管廊存在残余顶推力的工程实况，在已有研究的基础上提出了一种针对顶管施工管廊在盾构下穿作用下的简化计算方法。首先采用Loganathan公式[1]获得隧道开挖引起邻近土体的自由位移，把土体自由位移附加在管廊上，将既有管廊简化成无限长的Euler-Bernoulli梁搁置在Pasternak地基模型，同时考虑顶管施工后管廊内部残余顶推力对其变形响应的影响[24]，结合两阶段法获得管廊变形响应的简化计算方法。通过与实测数据对比，本文方法计算结果较为符合；与本文方法退化解对比，本文方法的解析结果更具有优越性。随后系统分析了地层损失率、管廊直径、隧道与管廊竖向间距变化对既有管廊受力变形的影响。研究结果可为快速预测既有管廊受到盾构下穿影响提供依据。

1 分析过程

1.1 土体自由位移的求解

Loganathan等[1]提出软土地区隧道开挖对周边土体竖向位移影响T(x,z)的表达式，即

(1)

式(1)中：R为隧道的开挖半径；H为隧道轴线的埋深；x为任意一点到隧道中心线的水平间距；z为任意一点距离地面垂直深度；ε为隧道开挖引起的地层损失比；υ为周围土体的泊松比。

考虑到实际工程大部分盾构隧道与邻近顶管管廊不垂直的情况，如图1所示，当隧道轴线与管廊轴线存在夹角θ时，式(1)可修正为

(2)

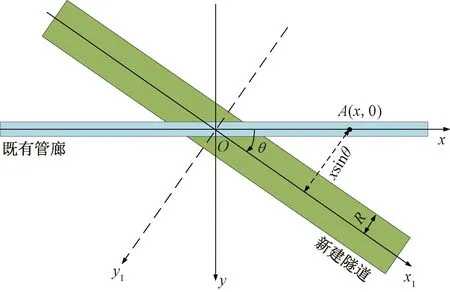
图1 新建隧道与既有管廊相交示意图Fig.1 The diagram of position between the new tunnel and the existing pipeline

1.2 既有管廊受力控制方程的建立

Pasternak地基模型相比传统的Winkler地基模型增加考虑了土体剪切作用，更能准确反映管廊与周边土体的相互作用，如图2所示。基于此，现做出以下假设。

图2 简化计算模型Fig.2 Simplified calculation model

(1)假定管廊是刚度为EI、直径为D的圆形截面弹性梁搁置在Pasternak地基模型上。

(2)Pasternak地基模型则是由k、G两个参数组成，且不考虑剪切层的压缩变形。

(3)采用无限长Euler-Bernoulli梁模拟管廊的变形，且不考虑管廊与周围土体脱空的现象。

(4)无限长管廊两端为自由状态，且管廊轴线附加应力可直接通过Loganathan公式[1]获得。

根据材料力学知识知, 管廊纵向位移w(x)满足曲率方程

(3)

式(3)中：M表示单元体所受的弯矩；EI表示管廊抗弯刚度。

其单元体平衡方程如下。

静力平衡：

Q+dQ+q(x)Ddx=Q+p(x)Ddx

(4)

弯矩平衡：

(5)

式中：Q为单元体所受的剪力；N为管廊受到的轴力；dx为单元体宽度；dQ和dM分别为单元体沿着x方向的剪力和弯矩增量；q(x)为管廊所受到的附加应力；p(x)为地基反力。

对于Pasternak模型来说，其地基反力p(x)可表示为

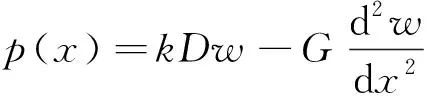
(6)

管廊线处受到的竖向附加荷载q(x)可表示为

(7)

式(7)中：T(x)为盾构开挖引起管廊轴线处的土体自由位移。

综合式(3)～式(6)，可知管廊竖向位移的控制方程为

(8)

根据文献[9], 土体弹簧刚度k和剪切刚度G可取为

(9)

式(9)中：Es为均质土体的弹性模量；νs为均质土体的泊松比；t代表剪切层厚度。

图3 既有管廊差分示意图Fig.3 Differential diagram of existing pipeline

考虑到式(8)为四阶微分方程，可采用差分法求解方程获得其数值解，将既有管廊简化成无数份单元长度l=L/n，如图3所示，n为隧道被分割的单元份数，L为管廊长度，管廊离散有n+5个节点单元(首尾共有四个虚拟单元)。

因此，式(8)差分结果为

(10)

考虑到既有管廊无限远两端受到下卧隧道开挖影响极小时，管廊两端的剪力和弯矩均可简化为0，即

(11)

那么式(10)可化为

(Kc+Ke-Gr)·W=Q

(12)

式(12)中：Kc、Ke和Gr分别为管廊单元刚度矩阵、地基的刚度矩阵和土体剪切刚度叠加管廊轴力的混合矩阵；W和Q分别为管廊竖向位移和管廊所受竖向附加应力列向量。

式(12)中的刚度矩阵分别为

(13)

(14)

(15)

(16)

(17)

至此管廊的竖向位移w(x)便可得到差分解。同时，也可得到管廊弯矩和剪力为

(18)

(19)

值得注意的是，当隧道轴力N=0时，本文解析将退化成只有附加应力作用下的既有管廊变形响应(EB-P模型)。当轴力N=0且Pasternak地基模型中G=0时，管廊-土体之间相互作用将退化成Winkler地基模型(EB-W模型)。

2 算例验证

为了验证本文方法的正确性，收集了杭州某地区隧道下穿电力管廊工程的实测数据与本文方法及其退化解计算结果进行了对比分析。

2.1 工程案例1分析

本工况中隧道开挖采用盾构法施工，隧道近似垂直下穿一条大管径电力管廊，管廊为圆形截面，材质为30 GPa混凝土，管廊直径D=4.8 m，管道壁厚t=0.4 m，管道泊松比ν=0.17，管廊轴线埋深z0=9.5 m。开挖隧道半径R=3 m，隧道轴线埋深H=20.4 m，根据当地地层参数加权平均后可取土体弹性模量Es=16.4 MPa，土体泊松比为νs=0.33，隧道开挖引起的地层损失率可取ε=1%。由志波由纪夫等[25]的计算方法可知既有管线抗弯刚度为4.05×1011N·m2。考虑到既有管廊顶推力的影响，可取既有管廊轴力为10 ×106N。

图4(a)为本文方法及其退化解EB-P模型计算结果与实测数据结果对比图。由图4(a)可以看出，本文方法及其退化解EB-P模型计算得到的管廊位移变化趋势与监测数据一致，且管廊位移峰值均出现在管廊中心线附近。在未考虑管廊轴力作用时，EB-P模型计算结果与实测结果存在偏差，而本文方法考虑管廊轴力后，其计算结果与实测数据较为符合，计算精度也有较大提高。笔者认为造成这一现象的原因在于本文提出的既有管廊轴力作用下，管廊纵向长度上挤压的更加紧密，会使得既有管廊抵抗变形的能力增强，显然会减小管廊竖向变形。总的来说，本文方法与EB-P模型的计算结果均能较好的预测管廊变形响应，但本文方法因为多考虑了轴力作用，其计算结果更具有优越性。

图4 管廊位移计算及实测数据对比曲线Fig.4 Comparison of the calculated and measured results of deformation of pipeline

2.2 工程案例2分析

本工况中隧道开挖同样采用盾构法施工，隧道近似下穿一条大管径电缆管廊，隧道与管廊夹角55°，管廊为正方形截面，材质为30 GPa混凝土，管廊边长D=4.4 m，管道壁厚t=0.4 m，管道泊松比ν=0.17，管廊轴线埋深z0=10.8 m。开挖隧道半径R=3 m，隧道轴线埋深H=18.6 m，根据土体参数加权平均后可取土体弹性模量Es=8.4 MPa，土体泊松比为νs=0.28，由于本工程土体均为软黏土，隧道开挖时采取了较好的保护措施，隧道开挖引起的地层损失率可取ε=0.5%。由志波由纪夫等[25]的计算方法可知既有管线抗弯刚度为9.0×1011N·m2。考虑到既有管廊顶推力的影响，可取既有管廊轴力为10×106N。

图4(b)为本文方法及其退化解EB-W模型计算结果与实测数据结果对比图。由图4(b)可以看出，本文方法及其退化解EB-W模型计算得到的管廊位移变化趋势与监测数据一致，两种方法计算得到的管廊位移峰值均出现在管廊中心点。EB-W模型计算结果与实测结果存在较大偏差，而本文方法的计算结果与实测数据较为符合，其计算精度明显高于EB-W模型的结果。笔者认为造成这一现象的原因是由于EB-W模型是将土与结构相互作用采用Winkler地基模型模拟，其忽视了土体之间的剪切效应，而土体间的剪切效应在研究土与结构相互作用时不可忽略[5-12]。总的来说，相比于EB-W模型，采用本文方法预测管廊变形响应更加符合实际。

3 参数分析

为了研究既有管廊应力应变与关键工程参数的关系，建立如下工程案例：下卧开挖隧道半径R=3 m，既有管廊隧道(截面圆形)直径为D=4.8 m，既有管廊和开挖隧道轴线埋深分别为z=15 m和H=25 m，土体泊松比为νs=0.33，隧道和管廊平面夹角α=90°，土体模量Es=20 MPa，既有管廊抗弯刚度为EI=4.05×1011N·m，新建隧道造成地层损失率为ε=1%。

3.1 地层损失率的影响

为研究不同地层损失率对管廊受力变形的影响，选取5组与地层损失率数据，分别取地层损失率ε=0.5%、1.0%、1.5%、2.0%、2.5%进行参数分析。

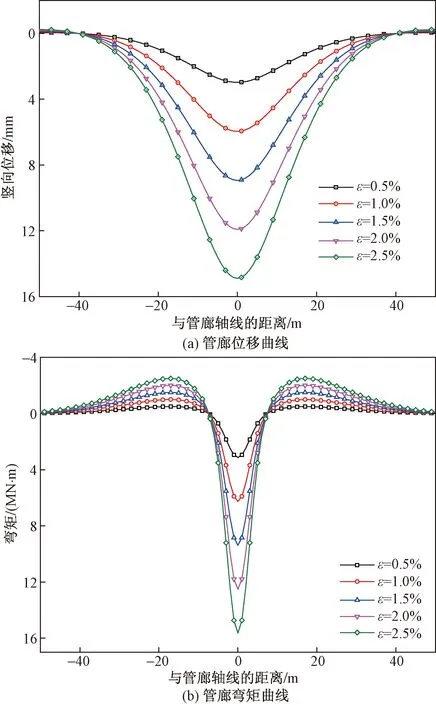
图5 不同地层损失率下管廊位移和弯矩曲线Fig.5 The curve of pipeline displacement and bending moment in different volume loss

图5为不同地层损失率情况下既有管廊竖向位移及弯矩的变化曲线。从图5可以看出，管廊竖向位移和弯矩变化分布图呈现轴对称的特点，在管廊中心线处，竖向位移和弯矩值均达到最大值；随着地层损失率的增大，管廊竖向位移量和弯矩均会随之线性增大。笔者认为这是根据土体位移场变化公式可知，随着地层损失率的增大，管廊轴线处所受的附加应力也会线性增大，致使每个位置处的管廊竖向位移和弯矩值也会与地层损失率线性相关。从图5还可以看出，由于管廊中轴线处的竖向位移和弯矩均达到峰值，因此在实际工程中，应尽可能在管廊中轴线处埋置相应的应力应变器，一旦测值达到预警值时，尽快采取相应措施以防止管廊产生更大变形；另外，尽量减小隧道开挖对周边土体的扰动以减小地层损失率，进一步保证既有邻近建筑物的安全性。

3.2 管廊直径的影响

为了研究不同管廊直径对管廊受力变形的影响，选取5组不同管廊直径数据，分别取为D=1.0、2.0、3.0、4.0、5.0、6.0 m进行参数分析。

图6 不同管廊直径下管廊位移和弯矩曲线Fig.6 The displacement and bending moment curve of pipeline in different diameter of pipeline

图6为不同管廊直径下盾构下穿引起既有管廊最大变形wmax及弯矩Mmax的变化曲线。从图6(a)可以看出，管廊直径的增大会引起管廊竖向位移的增大，随着管廊直径从1 m增大到6 m过程中，管廊最大变形从0.258 mm增大到9.311 mm，增幅为35倍，其增长速率不断增大。同样的可从图6(b)看出，随着管廊直径的不断增大，管廊最大所受弯矩也会不断增加，由最开始的最大弯矩值0.271×106N·m 增加到9.771×106N·m，增幅约为35倍，其增长速率也在不断增大。这是由于随着管廊直径的增大，既有管廊与周边土体的相互作用会显著增强，致使管廊的位移和弯矩内力都会迅速增大，说明管廊直径的改变是引起既有管廊受力变形的重大影响因素。在实际工程中尽量减小既有管廊直径来减小邻近土体卸载对既有管廊的影响。

3.3 隧道与管廊竖向间距的影响

为研究隧道与管廊竖向间距对管廊受力变形的影响，选取8组不同的间距d=nD，其中D为管廊直径，n为倍数，n=0.5、1、1.5、2、2.5、3、3.5、4进行参数分析。

图7 不同隧道与管廊竖向间距下管廊位移和弯矩曲线Fig.7 The displacement and bending moment curve of pipeline in different vertical clearance between tunnel and pipeline

图7为不同间距下管廊最大竖向位移wmax和最大弯矩Mmax变化曲线图。由图7(a)可以看出，随着隧道和管廊间距的增大，管廊最大竖向位移在不断减小，由最开始的最大竖向位移6.6 mm减小到 3.4 mm，降幅约为48%，减小速率不断减小。同样的可从图7(b)看出，增大隧道和管廊的竖向间距，管廊最大所受弯矩也会不断减小，由最开始的最大弯矩值7.0×106N·m减小到3.7×106N·m，降幅约为47%，增减小速率不断减小。这是由于随着隧道和管廊竖向间距的增加，盾构开挖引起既有管廊轴线处的附加应力在土层中逐渐消散，导致管廊最大竖向位移及弯矩均大幅度减小，说明在实际工程中可以通过增大隧道和管廊竖向间距来保护既有上覆管廊的安全。