基于状态指标的直升机减速器行星轮故障诊断

金小强， 袁志文， 熊天旸， 张先辉

(中国直升机设计研究所， 景德镇 333001)

直升机传动系统是一套单一无备份的动力传动链路，是整个直升机的骨架。主减速器是传动系统的重要组成部分，用于连接发动机和旋翼系统，是功率分配的关键环节。由于直升机的需用功率大，为了满足轻质重载的要求，直升机主减速器一般采用行星传动形式。行星齿轮的健康状态关系到整架直升机的安全，行星齿轮的故障诊断对于主减速器健康状态判断具有重要意义。

从20世纪80年代开始，英美等国一直积极发展直升机健康监测与使用系统(helicopter health & usage monitoring accelerometers,HUMS)，对齿轮箱、旋翼和发动机等关键部件进行健康监测、故障诊断与预测[1]。当前对行星齿轮的故障诊断，较多采用动力学建模分析方法。有的理论模型只考虑时变啮合刚度[2]，或只考虑啮合间隙[2-3]，以及同时考虑时变刚度和间隙的非线性动力学[4-5]，由于多种非线性因素的影响，很难采用解析方法求解，或者所获得的模型数值解的结果与故障特征的规律相符，但解析解的精度不是很理想[5-6]。中国很多学者采用信号分析的方法对行星齿轮箱故障进行诊断。文献[7-8]对行星轮系的裂纹故障进行诊断，提取了行星齿轮的特征频率，对故障诊断取得了一定的效果。文献[9-10]采用角域同步平均或迭代希尔伯特变换的方法对行星齿轮箱振动信号进行了处理，提取了齿轮箱的故障特征。文献[11]采用Teager能量算子和随机共振增强方法提取了齿轮箱的故障特征频率，对齿轮箱进行了故障诊断。文献[12-13]中采用模态分解方法对齿轮箱故障振动信号进行分解，提取故障特征信号，取得了较好的效果。以上方法侧重于齿轮箱故障特征频率的提取，在直升机工程应用中由于工况复杂，且多动部件同时运转，导致齿轮箱的故障频率信号往往微弱或与其他信号频率接近易混淆，特征频率信号提取困难。由于行星齿轮箱的结构复杂，各种信号相互耦合[14]，信号的幅值和频率相互调制[15-16]，频域的信号只能反映轮齿的部分故障。

现采用一种基于状态指标的方法对行星轮齿故障进行诊断分析。对利用角域同步平均方法对采集的行星轮振动信号进行预处理，选取合适的状态指标进行计算，并与行星轮健康状态下的阈值进行对比，验证该诊断方法的有效性。

1 行星齿轮的故障模式

行星轮系传动的优势在于均匀传递载荷，由于制造和装配等各种原因，非均载状态下行星齿轮将由于疲劳而产生各种故障。齿轮因疲劳引起的四类主要故障模式包括擦伤、点蚀、磨损、断齿[17]。对点蚀的检测与辨识具有挑战性，点蚀是一类因重复接触导致的齿面及其附近材料的疲劳破坏。按严重程度分为以下4类[18-19]：①微点蚀，该损伤在放大镜下观测，表面可见细小的微凹点区块，一般为0.002 54 mm深凹坑，指示出此时表面处于边缘润滑情形。②点蚀，点蚀指的是剥去的材料表面区块的直径为0.381～0.762 mm。点蚀出现在轮齿承受过应力的局部区域。③剥落，该损伤模式是点蚀严重的极端情形。该损伤模式表现为剥离凹坑区块较浅但面积更大且通常形状不规则。剥落与点蚀之间的约定划分界线是凹坑直径0.762 mm。当有剥落的齿啮合时，齿剥落部分不能承受载荷。这将使载荷快速重新分布并使得大应力集中在凹坑的边缘。④破坏性点蚀，该损伤模式拥有比初始点蚀更大的凹坑区块，且往往扩展到轮齿的齿根部。这些更大的坑痕常常是由更为严重的过载条件所致，且表现为大小不稳定的剥落块。当应力循环增强时，破坏性点蚀将持续扩展直至齿轮廓被破坏。另外，根据文献[20]所述，磨损是指金属层表面均匀地被移去。

2 状态指标的选取

英国南安普敦大学学者Stewart首次将状态指标应用于传动系统，他观察到健康的传动系统的振动信号边频带幅值小，出现某种故障时边频带幅值明显增加，这一现象在局部缺陷如单齿故障时尤其如此。本文中选取的状态指标如下。

(1)均方根(root mean square，RMS)。均方根描述信号的能量成分，用来评估部件的整体状态。均方根对早期故障不灵敏，但可用于大致跟踪总体的故障演化。其计算式为

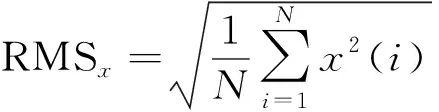
(1)

式(1)中：x(i)的原始采样数据；N为数据点数。

振动信号的均方根值是对所测试齿轮箱总体状态的一种比较好的描述。该参数对齿轮箱载荷和转速的变化是敏感的。该参数主要用来监测总体振动水平。当振动能量达到临界值(阈值)，齿轮箱要停止运行并处理可能的故障或破坏。一般需要记录和监测总体振动信号的均方根值的时间历程。当齿轮箱磨损严重和/或出现点蚀损伤时，振动水平将变化较大。当点蚀损伤持续演化，总体振动水平会快速变化。这一迹象可以用来确切地判断点蚀的出现。

(2)FM0(figure merit zero)状态指标。该参数定义为信号峰值除以啮频及其谐波的能量的商。表达式为

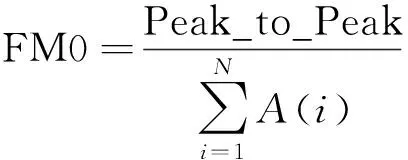
(2)

式(2)中:Peak_to_Peak为信号峰峰值;A(i)为第i个啮频湝波的幅值。

(3)差分信号的能量算子(energy operator,EO)。对时域同步平均信号滤掉齿轮啮合频率分量及其谐波成分、驱动轴频率分量及其二阶谐波，再滤掉围绕啮合频率成分的一阶边频带分量，便构成了差分信号。无损伤的情况下，差分信号应该保持为由正态分布描述的高斯白噪声。如果差分信号的频谱中包含有各种显著的分量，则可认为损伤是引起这些分量的主要原因。

能量算子为信号平方差序列的归一化峭度，该平方差序列中每一点为原始信号两相邻点平方差值[25]。表达式为

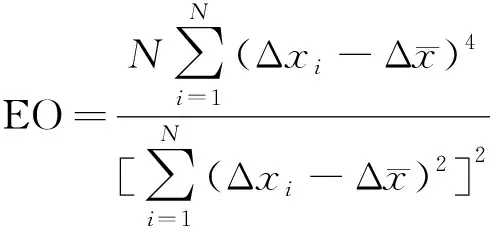
(3)

能量算子是一类自相关函数残差，用以揭示感兴趣信号成分的幅值调制和相位调制情况。对于行星齿轮，占主导地位的振动是齿轮的啮合。大的能量算子值指示出严重的点蚀或刮伤。

(4)数据算法1阶(data algorithm one，DA1)指数。DA1是时域同步平均(time domain synchronization average，TSA)信号减去其均值后的均方根值，定义为

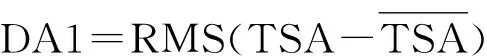
(4)

DA1检测信号中总体能量的增加情况，用来指示分布式的齿轮故障。

3 阈值计算方法

对于阈值的确定，国外进行了大量的技术研究。对于振动诊断工具而言，最简单获得阈值的方法是在正常运转状态下收集基线振动，并把超过正常运转状态的值设定为阈值。在故障发生之前这个方法一直有效，从一个机队的状态指示器来看，状态指示器的值也在正常变化范围内。但是HUMS制造商也看到过在健康减速箱部件状态指示器的指示范围存在极大差异。受到直升机故障数据的限制，诊断工具的发展受限于地面测试环境的种子试验。

针对本项目中选取的直升机动部件健康状态指标，选取了高斯分布统计方法，对行星齿轮故障植入试验采集到的振动数据进行动态阈值计算。

高斯分布统计阈值计算的方法实则是利用了正态分布在统计学中的定义、性质以及分布曲线。

若随机变量(原始采样数据)x服从一个数学期望为μ、方差为σ2的正态分布，其概率密度函数f(x)为

(5)

则这个随机变量就称为正态随机变量，正态随机变量服从的分布就称为正态分布。

正态分布是数理统计理论中一个非常重要的概率分布。在自然现象和社会现象中，大量随机变量都服从或近似服从正态分布。

在正态分布中，共有99.74%的变量位于正态分布的(μ-3σ，μ+3σ)范围内，即“3σ”准则。 准则又称为拉依达准则，它是假设一组检测数据只含有随机误差，对其进行计算处理得到标准偏差，按一定概率确定一个区间，认为凡是超过这个区间的误差，就不属于随机误差而是粗大误差，含有该误差的数据应予以剔除。

则阈值th计算公式为：th=μ+kσ(k一般取值3～5)。

4 试验过程

由于很难获取直升机真实飞行过程中的故障数据，采用故障植入的方法，模拟行星齿轮的损伤。在主减速器故障植入试验台上开展试验，采集试验数据。主减速器故障植入试验台如图1所示。

图1 主减速器故障植入试验台Fig.1 Fault seeded test bench of main gearbox

主减速器故障植入试验台主要包括试验台架、电机与控制系统、负载系统、主减速器模型、主减速器故障模拟件；电机运转转速精度优于(包含)(1‰±1)r/min，行星减速器输出端转速为200～500 r/min。

表1为行星齿轮试验件的基本参数，利用电火花刻蚀技术对试验件进行故障植入，行星齿轮试验件的故障植入状态如下：行星齿轮裂纹故障，深度25%；行星齿轮裂纹故障，深度50%；行星齿轮齿面剥蚀故障，深度5%；行星齿轮齿面剥蚀故障，深度10%。

行星齿轮试验件如图2所示，在试验台额定载荷100%的功率状态下，输入转速为2 850 r/min，进行主减速器故障植入试验。在试验台上安装12个单轴振动传感器，1个转速传感器。数据采样率为20 000/s，每个试验状态采集时间为10 min。为了保证数据的准确性，各试验状态均有一次重复试验。

表1 行星齿轮基本参数Table 1 Basic parameters of planetary gears

图2 行星齿轮试验件Fig.2 Test samples of planetary gear

配有光电传感器、温度传感器分别对主减速器系统的输出转速、齿轮箱的输入、输出温度进行监控，加速度传感器分别采集齿轮箱输入、输出端齿轮、轴承的振动数据。

5 数据分析及结果

对获取的试验台验证试验数据进行分析，取正常状态行星齿轮，裂纹25%的行星齿轮，裂纹50%的行星齿轮分别运行时的试验振动数据，作为分析对象。将以上数据作为输入，分别计算四个状态指标的数值。由于试验数据较多，含有植入裂纹故障行星齿轮的试验数据按照每100圈作为一组数据，每个裂纹故障状态取了260组数据。

以正常状态的行星齿轮振动数据为基础，计算行星齿轮的振动基线，作为行星齿轮健康状态的判断阈值。图3为植入裂纹故障的行星齿轮振动数据，图4为植入剥蚀故障的行星齿轮振动数据。

图3 植入裂纹故障的行星齿轮振动数据Fig.3 Vibration data of planetary gears with implanted crack fault

图4 植入剥蚀故障的行星齿轮振动数据Fig.4 Vibration data of planetary gears with implanted erosion faults

图3、图4中振动阈值采用高斯分布统计的方法进行计算，区均值加上3倍的标准差。由于状态指标的定义不同，计算的故障状态的振动值与阈值的对比中，有的是高于阈值为故障，例如RMS值和DA1值，有的是低于阈值为故障状态，例如FM0值和EO值。从图3中，状态指标RMS，FM0，差分信号EO，DA1指数值能够与阈值明显区分，能够判断出齿轮在裂纹状态下的故障情况。从图4中，状态指标RMS，FM0，差分信号EO，DA1指数值能够与阈值明显区分，能够判断出齿轮在剥蚀状态下的故障情况。

6 结论

对行星轮齿的裂纹和剥蚀的单个故障进行了研究，根据以上数据分析，采用状态指标对行星轮轮齿的植入故障进行诊断，可以明显区分出单个故障状态下齿轮的状态指标值和健康阈值，具有很好的诊断效果，对于两个故障均出现的复合故障还需要进一步研究。基于状态指标的行星轮故障诊断方法，能够诊断出直升机主减速器行星轮的裂纹和剥蚀的单一故障，对提升直升机的安全性，具有较好的效果。