间接荷载作用下梁的内力影响线的静力解法研究

2022-02-05魏鹏云

工程与试验 2022年4期

魏鹏云，李林

(塔里木大学水利与建筑工程学院，新疆阿拉尔 843300)

1 引言

影响线是结构力学的一个重点和难点内容。对于梁的内力影响线，可以按照荷载是否直接作用在梁上而分为直接荷载作用下梁的内力影响线及间接荷载作用下梁的内力影响线，间接荷载作用下梁的内力影响线有些教材又称为结点承载方式下梁的内力影响线[1-3]。许多同学初学影响线时会感到困惑，尤其是教材里间接荷载作用下梁的内力影响线的做法都是采用先给结论后证明的思想[1-6]，这对初学者来说并不容易从根本上理解，很多同学只是记住了相关结论。

影响线的求解方法主要有静力法和机动法，本文采用静力法从3个不同角度直接求解间接荷载作用下梁的内力影响线，这3种求解思路可以加深学生对间接荷载作用下梁的内力影响线的理解，开阔学生的思维，培养学生多角度思考问题的能力，也可以帮助教师拓宽间接荷载作用下梁的内力影响线的教学思路。

2 从力的传递角度直接求解

图1所示为一桥梁结构的承载示意图，荷载直接在纵梁上面移动，纵梁两端支在横梁上面，横梁由主梁支撑，则荷载会通过横梁传递给主梁，此时主梁的受力就属于结点方式承载或受间接荷载作用。已知纵梁由A1B1、B1C1及C1D1三段组成，现拟求主梁E截面的弯矩ME和剪力FQE的影响线。

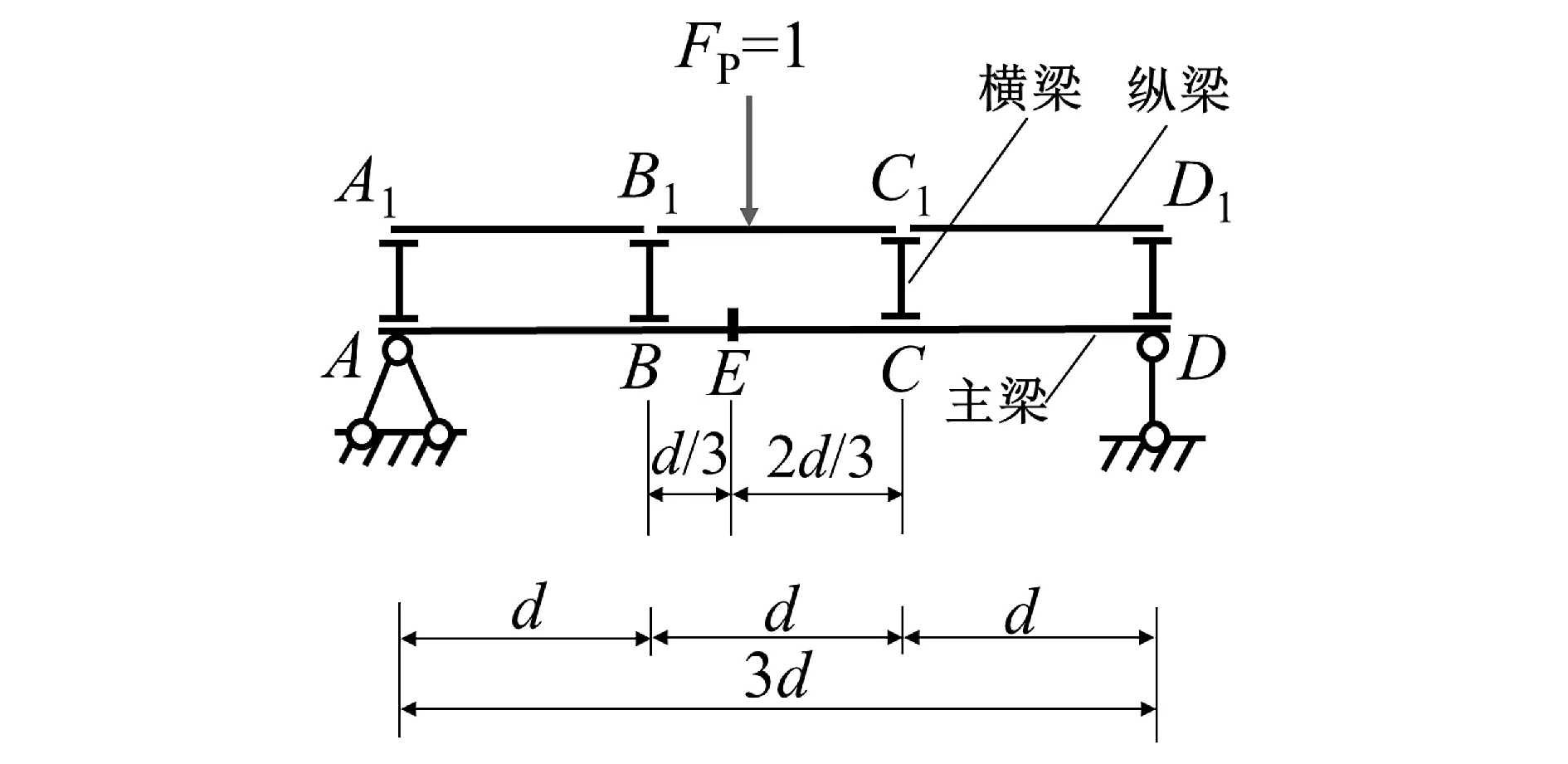
图1 某桥梁结构的承载示意图

2.1 建立坐标系

以A点为坐标原点，水平向右为x轴正向。

2.2 求支座反力FRA和FRD

无论FP=1运动到纵梁的任何位置x处，将整个结构整体看成研究对象，对D点取矩，则有：

(1)

由式(1)可得：

(2)

对A点取矩，则有：

(3)

由式(3)可得

(4)

关于支座反力的求法还可以从力的传递角度直接求解得到，具体的求解思路与后述的E截面的弯矩ME和剪力FQE的影响线的求解思路一致，故支座反力不再从力的传递角度去求解。

2.3 FP=1在纵梁A1B1段运动

当FP=1在纵梁A1B1段运动时纵梁及主梁的受力情况如图2所示。

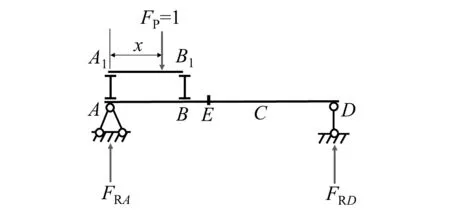
(a) FP=1在纵梁A1B1段运动示意图

(b)纵梁A1B1的反力示意图图2 FP=1在纵梁A1B1段运动时纵梁和主梁的受力分析图

为了获得FP=1在纵梁A1B1段运动时主梁的内力影响线，做出主梁的受力情况，如图3所示。

图3 FP=1在纵梁A1B1段运动时主梁的受力示意图

利用截面法，将主梁AD从E点截断后，取右部分为隔离体作为研究对象，如图4所示。

图4 DE段隔离体受力示意图

观察隔离体，对E点取矩，则有：

(5)

由式(5)可得：

(6)

列竖向力的平衡方程，则有：

(7)

由式(7)可得：

(8)

2.4 FP=1在纵梁B1C1段运动

当FP=1在纵梁B1C1段运动时，纵梁及主梁的受力情况如图5所示。

(a)FP=1在纵梁B1C1段运动示意图

(b) 纵梁B1C1的反力示意图图5 FP=1在纵梁B1C1段运动时纵梁和主梁的受力分析图

为了获得FP=1在纵梁B1C1段运动时主梁的内力影响线，做出主梁的受力情况，如图6所示。

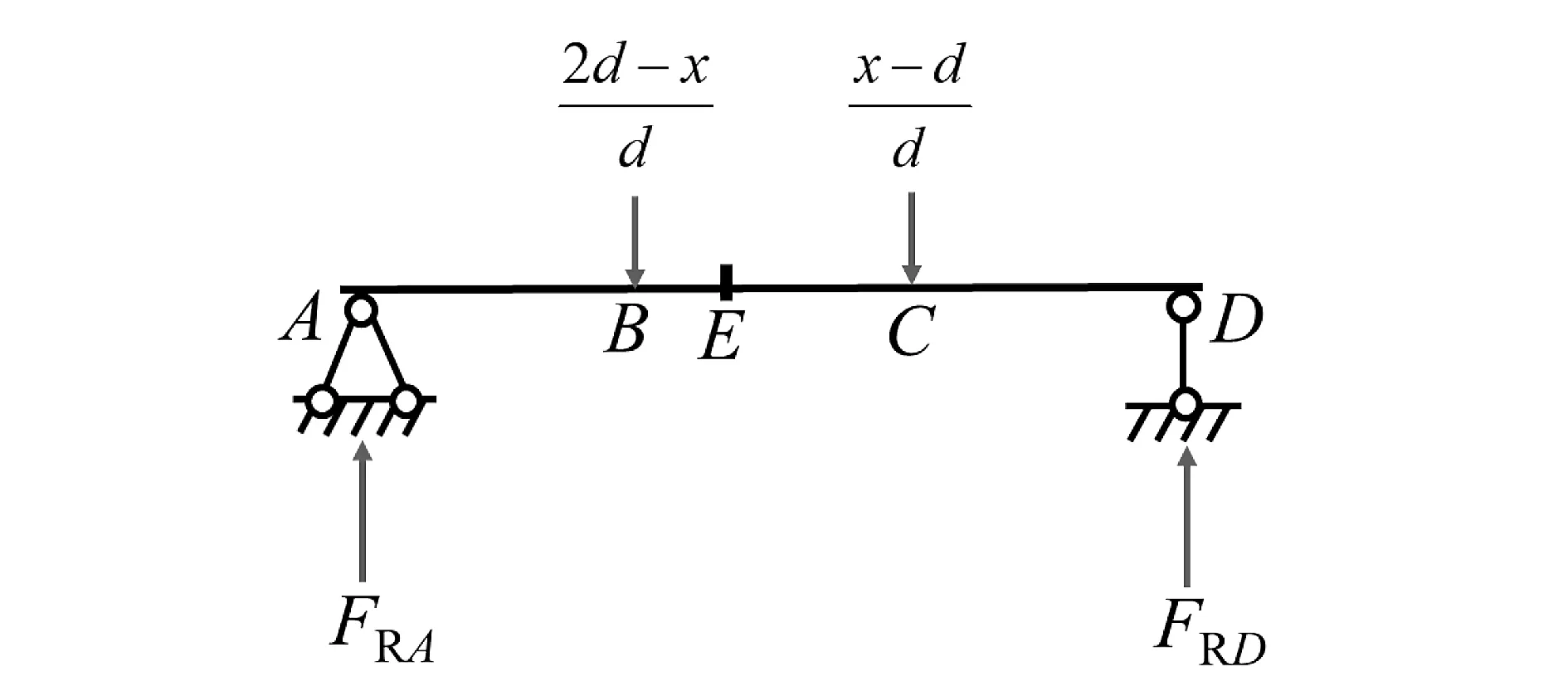
图6 FP=1在纵梁B1C1段运动时主梁的受力示意图

利用截面法，将主梁AD从E点截断后，取右部分为隔离体作为研究对象，如图7所示。

图7 DE段隔离体受力示意图

观察隔离体，对E点取矩，则有：

(9)

由式(9)可得：

(10)

列竖向力的平衡方程，则有：

(11)

由式(11)可得：

(12)

2.5 FP=1在纵梁C1D1段运动

当FP=1在纵梁C1D1段运动时，纵梁及主梁的受力情况如图8所示。

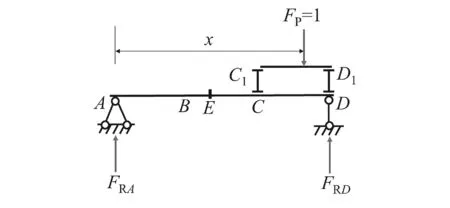
(a)FP=1在纵梁C1D1段运动示意图

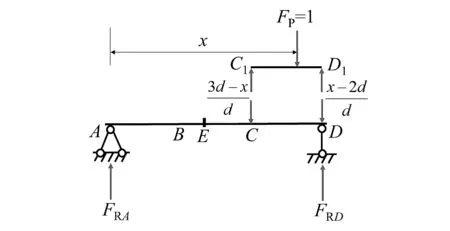
(b) 纵梁C1D1的反力示意图图8 FP=1在纵梁C1D1段运动时纵梁和主梁的受力分析图

为了获得FP=1在纵梁C1D1段运动时主梁的内力影响线，做出主梁的受力情况，如图9所示。

图9 FP=1在纵梁C1D1段运动时主梁的受力示意图

利用截面法，将主梁AD从E点截断后，取右部分隔离体作为研究对象，如图10所示。

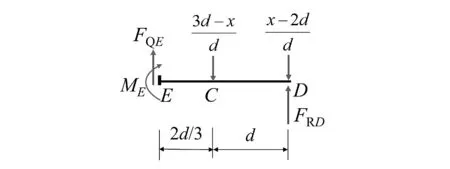
图10 DE段隔离体受力示意图

观察隔离体，对E点取矩，则有：

(13)

由式(13)可得：

(14)

列竖向力的平衡方程，则有：

(15)

由式(15)可得：

(16)

2.6 做ME和FQE的影响线

(17)

(18)

由式(17)和式(18)可做ME和FQE的影响线，如图11、图12所示。

图11 ME的影响线

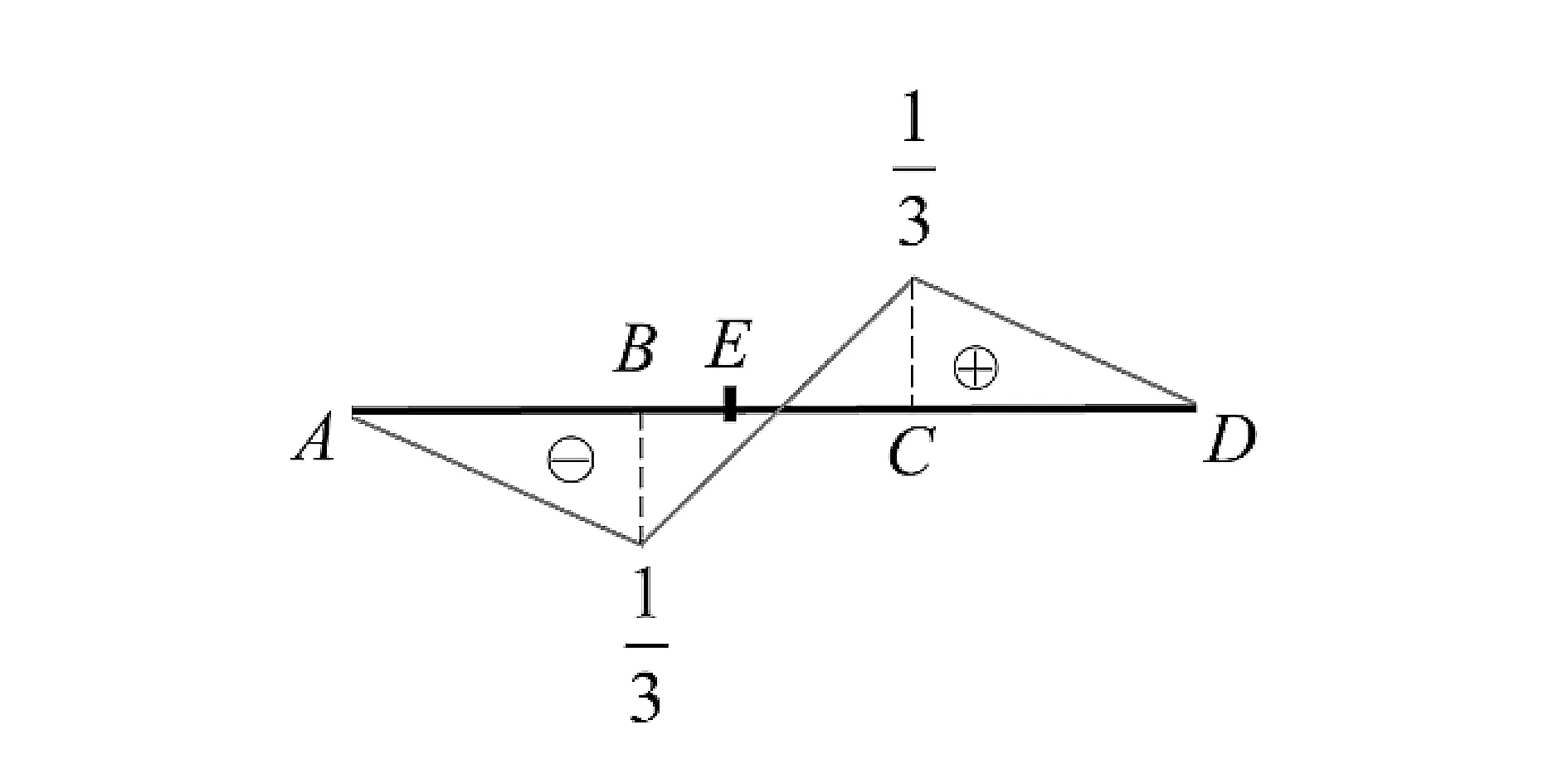
图12 FQE的影响线

3 将FP=1等效为两个杆端集中力的求解方法

单位力FP在每段纵梁上面移动时，可将单位力等效为两个作用在纵梁两端的竖向集中力。依然以图1所示的某桥梁结构的承载示意图为例来说明此法的具体操作步骤。关于坐标系以及支座反力FRA和FRD的求法与前面一致，这里不再赘述。接下来看如何做E截面弯矩ME和剪力FQE的影响线。

3.1 FP=1在纵梁A1B1段运动

当FP=1在纵梁A1B1段运动时，FP=1可等效为图13所示。观察图13可知，要想求得ME和FQE的表达式，只需利用截面法从E截面截断，取左部分或右部分为隔离体，进而列平衡方程即可，具体的求解过程不再赘述。

图13 FP=1在纵梁A1B1段运动时力的等效示意图

3.2 FP=1在纵梁B1C1段运动

当FP=1在纵梁B1C1段运动时，FP=1可等效为图14所示。观察图14可知，要想求得ME和FQE的表达式，只需利用截面法从E截面将纵梁及主梁均截断，取左部分或右部分作为隔离体，进而列平衡方程即可，具体的求解过程不再赘述。

图14 FP=1在纵梁B1C1段运动时力的等效示意图

3.3 FP=1在纵梁C1D1段运动

当FP=1在纵梁C1D1段运动时，FP=1可等效为图15所示。观察图15可知，要想求得ME和FQE的表达式，只需利用截面法将主梁AD从E截面截断，取左部分或右部分作为隔离体，进而列平衡方程即可，具体的求解过程不再赘述。

图15 FP=1在纵梁C1D1段运动时力的等效示意图

3.4 做ME和FQE的影响线

通过上述计算分析可知，ME和FQE的影响线就是图11和图12，故这里不再重复。

3.5 与前一种求解方法的对比说明

图13-图15所展示的是两个集中力作用在纵梁的两个端点上，此端点正好是横梁的位置，相当于这两个集中力直接作用在主梁上，也就是图13与图3、图14与图6、图15与图9是完全等价的受力状态。那么，在取隔离体求解时可以不画横梁，也可以画上横梁。以FP=1在纵梁B1C1段运动(见图14)为例，将主梁AD从E点截断后取右部分为隔离体，如图16所示，此隔离体上画上了横梁。观察图16，对E点取矩便可求得ME的表达式。列竖向力的平衡方程，可得FQE的表达式。显然，ME与FQE的表达式就是式(10)和式(12)的形式，由此也可以说明本方法的正确性。

图16 DE段隔离体受力示意图

4 直接切断主梁和纵梁的求解方法

单位力FP=1在每段纵梁上面移动时，为了获得待求某量值的影响线，可将纵梁和主梁都切断，此时纵梁和主梁都会暴露出来内力，而纵梁的内力可以先求出来作为外荷载，从而再通过平衡方程求得待求某量值的影响线。依然以图1所示的某桥梁结构的承载示意图为例来说明此法的具体操作步骤。关于坐标系以及支座反力FRA和FRD的求法与前文一致，这里不再赘述。接下来看如何做E截面弯矩ME和剪力FQE的影响线。

为了统一计算及便于与主梁E截面的弯矩ME和剪力FQE进行区分，将纵梁E1截面的弯矩和剪力分别记为ME1和FQE1。

4.1 FP=1在纵梁A1B1段运动

FP=1在纵梁A1B1段移动的示意图如图17所示。利用截面法将纵梁B1C1段和主梁AD分别从E1位置和E位置截断，取右侧为隔离体作为研究对象，如图18所示。

图17 FP=1在纵梁A1B1段运动的示意图

图18 E1E截面以右段隔离体受力示意图

由于FP=1在纵梁A1B1段移动，则纵梁B1C1段及C1D1段无外荷载作用，故纵梁E1截面处的剪力FQE1和弯矩ME1均为0。因而求ME和FQE时，可将纵梁E1C1段和C1D1段以及横梁去掉，此时隔离体图18将与图4完全一致，故这里不再赘述后面的求解。

4.2 FP=1在纵梁B1C1段运动

当FP=1在纵梁B1C1段移动时，需要分为FP=1在B1E1段和E1C1段(因为FP=1在E1点左侧和右侧时E1截面的弯矩和剪力的表达式不一致)。

4.2.1FP=1在纵梁B1E1段移动

当FP=1在纵梁B1E1段移动时，如图19所示。利用截面法将纵梁B1C1段和主梁AD分别从E1位置和E位置截断，取右侧为隔离体作为研究对象，如图20所示。

图19 FP=1在纵梁B1E1段运动的示意图

图20 E1E截面以右段隔离体受力示意图

纵梁B1C1段E1截面的弯矩ME1和剪力FQE1的求解如下：

将纵梁B1C1段从E1截面处截开，取E1C1段隔离体为研究对象，如图21所示。

图21 纵梁E1C1段隔离体受力示意图

观察隔离体图21，对E1点取矩，则有：

(19)

由式(19)可得：

(20)

列竖向力的平衡方程，则有：

(21)

由式(21)可得：

(22)

由式(20)和式(22)求得ME1和FQE1后，再观察隔离体图20，对E点取矩，则有：

(23)

由式(23)可得：

(24)

列竖向力的平衡方程，则有：

(25)

由式(25)可得：

(26)

4.2.2FP=1在纵梁E1C1段移动

当FP=1在纵梁E1C1段移动时，利用截面法将纵梁B1C1段和主梁AD分别从E1位置和E位置截断，取左侧为隔离体作为研究对象，如图22、图23所示。

图22 FP=1在纵梁E1C1段运动的示意图

图23 E1E截面以左段隔离体受力示意图

要想获得FP=1在纵梁E1C1段移动时E截面的弯矩

ME和剪力FQE，可仿照上文的做法：取纵梁的B1C1段或者E1C1段为隔离体，先求得E1截面的弯矩ME1和剪力FQE1，再观察隔离体(见图23)，对E点取矩，获得E截面弯矩ME的表达式，见式(27)，列竖向力的平衡方程，可得E截面剪力FQE的表达式，见式(28)。

(27)

(28)

观察式(24)和式(27)、式(26)及式(28)，可得：

(29)

(30)

对比发现，式(29)和式(10)完全一致，式(30)和(12)完全一致，由此可以说明本方法的准确性。

4.3 FP=1在纵梁C1D1段运动

FP=1在纵梁C1D1段移动的示意图如图24所示，利用截面法将纵梁C1D1段和主梁AD分别从E1位置和E位置截断，取左侧为隔离体作为研究对象，如图25所示。

图24 FP=1在纵梁C1D1段运动的示意图

由于FP=1在纵梁C1D1段移动，则纵梁A1B1段及B1C1段无外荷载作用，纵梁E1截面处的剪力FQE1和弯矩ME1均为0。因而求ME和FQE时，可将纵梁A1B1段和B1E1段以及横梁去掉，然后对E点取矩，可得到ME的表达式。列竖向力的平衡方程，可得到FQE的表达式。ME和FQE的表达式分别与式(14)和式(16)完全一致，具体求解过程这里不再赘述。