非线性回归算法在飞机载荷标定试验中的应用
2022-02-05韩聪玲刘克格刘彦鹏
韩聪玲,刘克格,刘彦鹏
(国机集团北京飞机强度研究所有限公司,北京 100083)
1 引 言
在飞机使用和研制过程中,通常需要进行载荷谱实测。载荷谱实测在当前工业应用中具有重要意义,载荷谱实测结论可以应用在以下方面:(1)寿命估算;(2)全尺寸试验;(3)可靠性设计;(4)耐久性评定;(5)计算机辅助设计。
根据飞机的空间力受载分析,通过应变桥路设计、载荷标定,建立关于实测载荷输入同应变(码值)输出的数据关系方程,并对方程求解,结合飞机实测飞行数据,可以获得飞行状态中相关部件实际运作中的载荷-时间历程,即实测载荷谱。
工程实践中,实测载荷与应变(码值)通常满足一定的线性函数关系,所以,利用标定试验数据,建立线性关系方程,即标定试验方程,最终解得回归系数,得到载荷-应变(码值)的函数关系,是本阶段试验的主要目的。这种基于多元线性回归的预测方法,在进行有效参数分析时,某种程度在分析过程中依赖技术人员的经验,通常在一定范围内误差可以控制在5%以内,结果较为满意。但对于载荷与应变(码值)之间有复杂的相关性时,会对最终载荷标定精度造成影响。文献[1]提出了一种“多元回归选元方法”,其基本思路是把回归变异系数作为选用依据,进行误差控制,选出最优自变量参与回归计算,从而得到最优解。基于该方法,目前已使用多型号的飞机载荷谱实测试验数据进行了成功的验证,验证的数据误差可控制在5%以内,结果较为满意。
在参数较多、载荷分量较小时,误差会偏大。同时,考虑到实际的结构部件和原材料等问题的影响,输入载荷与输出应变(码值)在某一特定数据值范围内会呈现出一定的非线性关系,因此本文对计算载荷与输出应变关系的方法进行新的尝试和探索,使用基于机器学习的大数据非线性回归分析模型建立载荷与应变(码值)的关系。
2 线性回归方法与结论
基于应变电测法的载荷谱实测试验,在标定试验过程中,根据飞机的受力情况,设计应变桥路。在应变、桥路设计的基础上,通过标定试验记录的试验数据,建立载荷应变函数方程,再通过此方程计算出飞机设备部件在实际运行时的载荷随时间的变化函数,称作载荷-时间历程。
对于标定试验而言,利用电阻应变片测量出飞机结构部件表面的应变(码值),再根据应变和应力的函数关系计算出结构表面的受力情况。应变片的电阻值会随结构表面的形变情况发生变化,电阻变化值可以进行物理量的换算,通过计算可以得到所测的物理量。原理是载荷=系数×应变,利用可控的已知载荷和应变数值求出未知系数。
以某飞机为例,设备结构所承受的外载一般分为空间6个分力,以某个部位为例,y向载荷分量剪力Q,忽略x向的载荷分量(相对较小),即把M、Q、T作为输入,相应的测试应变码值ε1、ε2、ε3作为输出。利用试验数据,基于逐步回归的数学建模,标定数据处理的数学模型为:
求出系数矩阵βij后,再用有偏估计或区间预测M、Q、T。在实际工作中,因为最终需要预测的是M、Q、T,所以模型变形为如下形式:
求解αij系数矩阵就是标定试验阶段的主要任务,最终通过最小二乘法计算得出。
大多数情况下,在标定试验数据中,某个信号量与载荷值的线性关系很明显。以某试验的某个截面试验数据为例,进行散点图绘制(如图1-图3所示),纵轴向代表M,theta_m_1、theta_m_2、theta_m_3横向从上到下依次代表应变ε1、ε2、ε3。
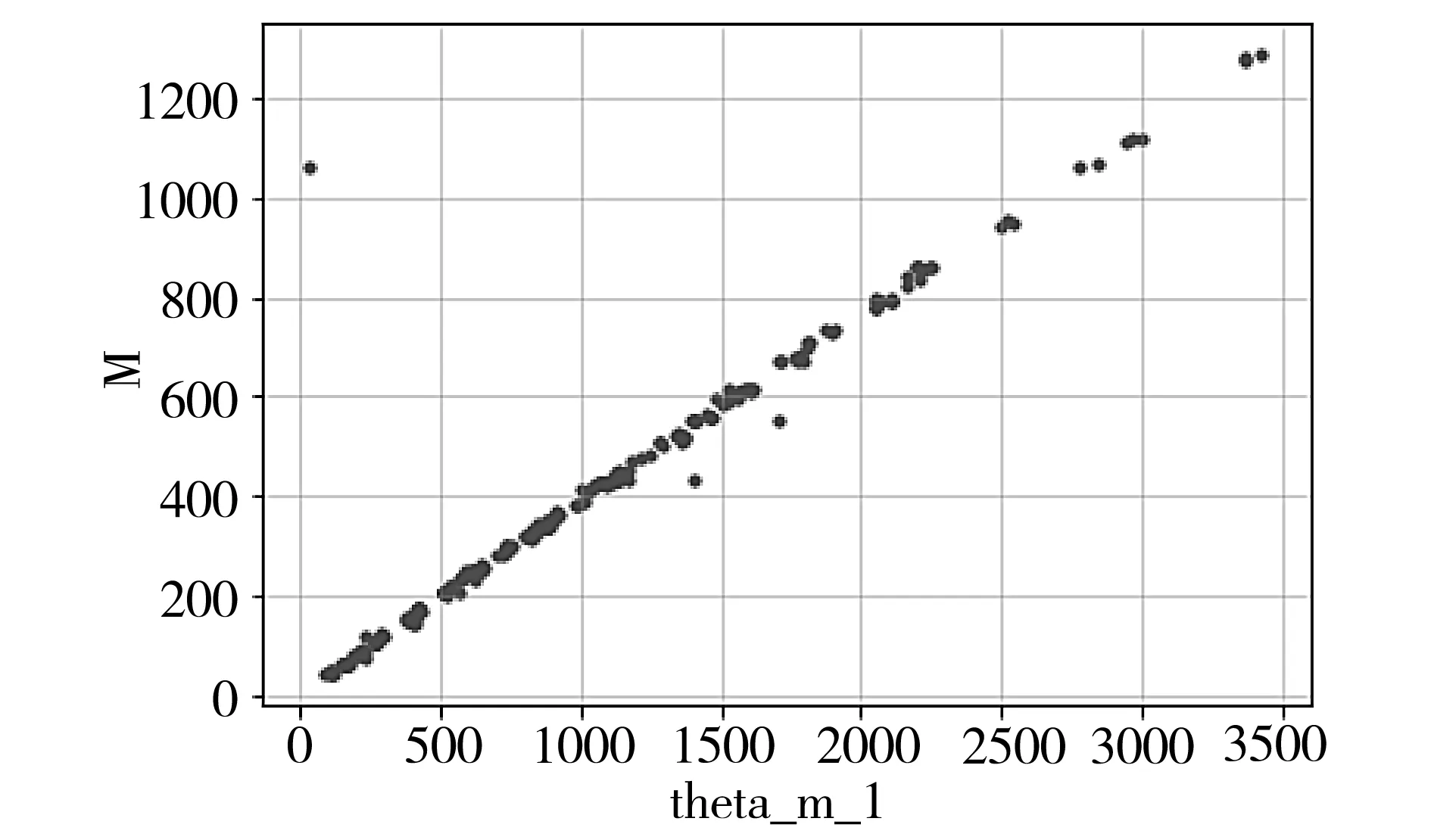
图1 数据关系的数据散点图
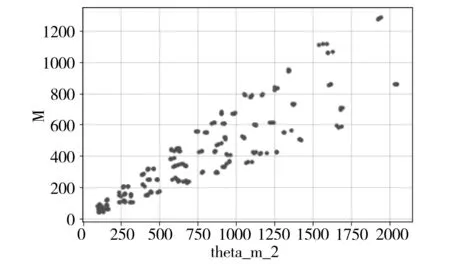
图2 数据关系的数据散点图
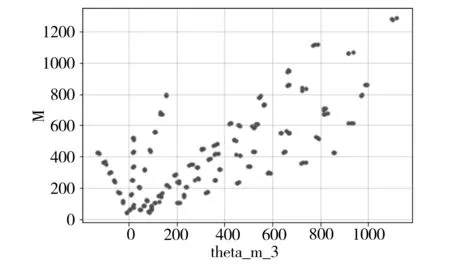
图3 数据关系的数据散点图
3 几种非线性回归模型
从图2、图3所示的ε2、ε3与M关系图可以看出,这两个分量的散点图较为分散。在试验过程中,会出现局部散点分布回归效果不理想的情况。如果单纯地使用线性回归计算标定试验方程,误差可能会偏大,有时会出现高于5%的误差。本文使用非线性回归模型进行计算,以提高回归精度。
回归分析是统计学中在观察和分析大量试验数据的规律后,得出自变量与因变量关系的过程。目前,在进行大数据回归预测时,常用的模型包括随机森林模型、极端随机树模型、GBDT模型、XGBoost模型等。
3.1 随机森林模型
随机森林是机器学习的经典算法,最早由Breiman提出,是基于决策树的算法,可以有效处理多个因素相互作用的非线性回归问题[3-6]。其具有运算速度快的优点,因此是处理大数据回归时最常用的算法。在处理多变量共线的问题时,不需要进行变量筛选。在解决回归问题时,随机森林模型(简称RFR)在计算一组输入输出的非线性回归关系时的计算过程如下:
(1)基于Bootstrap方法有放回地随机选择子样本,组建训练集,基于Bootstrap算法重复取样,形成一定数量的训练集,形成独立的回归决策树。
(2)在回归树M个特征中随机取得m个子特征,逐个计算子样本特征后,从计算结果中得到满足均方误差最小的条件,形成2个节点。
(3)重复调用步骤(2),直至满足模型预设停止条件,决策树计算结果完成。
(4)生长回归决策树:
(1)
3.2 极端随机树模型
极端随机树(ET或Extra-Tree)是基于决策树的集成算法,和随机森林方法类似,也是基于多棵决策树构成的,但是又有区别。极端随机树是将每棵树都使用全部训练样本,从而提高了对全部样本的利用程度,在一定范围提升了精度[7]。极端随机树模型通过提高各个决策树之间的结构差异,从而构建更大的随机性,将决策树泛化误差加权值为:
(2)
决策数据的差异加权平均:
(3)
集成后的泛化误差表示为:
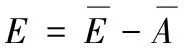
(4)
通过增加决策树的多样性以及单个决策树的精度,进一步提高模型最终集成的预测精度。
3.3 GBDT模型
GBDT(Gradient Boosting Decision Tree)是一种基于多次迭代决策树算法,其核心思想是基于多棵决策树的计算,实现累加取得最终结果,该算法所有树的结论累加作为最终结果。这种方法不但可以灵活处理各种类型的连续值数据,还可以很好地处理离散数据[8-11],可以在较短的训练和调参时间范围内,取得精度较高的结果。
GBDT的优点主要有:(1)灵活度高,不仅可以处理连续性数据,处理离散型数据时效果也很好。(2)可以使用较少的调参时间,达到较高的样品预测精度。GBDT的缺点主要表现在弱学习器方面,如果存在依赖关系,进行并行训练比较困难。
下述为GBDT计算过程。
输入数据集:
T={(x1,y1),(x2,y2),…,(xn,yn)}
(5)
损失函数表示为:
L(y,f(x))
(6)
首先,初始化:
(7)
(1)对于样本,计算损失函数的负梯度,计算残差:
(8)
(2)拟合下一轮学习器,满足损失函数最小:
(9)
(10)
(3)更新f(x)。
(4)计算回归树:
(11)
式中,m=1,2,3…M,M表示迭代次数。
3.4 XGBoost模型
XGBoost和GBDT很相似,目的是提高算法速度和效率。因此,XGBoost计算梯度时,使用了二阶偏导,使得梯度下降得更快更准,在预防过拟合方面表现很好,损失函数的计算精度高,适合计算系数矩阵[9-11]。
XGBoost模型如下:
(12)
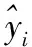
XGBoost的目标函数为:
(13)
目标函数包括误差项和正则化项,其中,正则化项可以表示成如下形式:
(14)
式中,T为叶子节点总数,ω为当前节点的特征数值。目标函数先进行二阶泰勒展开,再求偏导,可得目标的最优解:
(15)
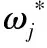
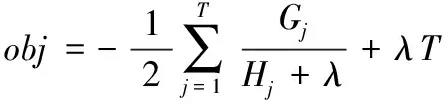
(16)
4 非线性回归模型的建立和计算
基于标定试验数据,去掉系统错误产生的数据,按照试验顺序选择一定比例的数据作为训练集,其余数据作为验证集,根据机器学习的理论,尝试构建4种非线性回归预测模型。选取随机森林、极端随机树、XGBoost、GBDT回归预测模型进行训练验证,并计算误差情况分析回归效果。如果误差在合理范围内,则流程结束,否则需要根据经验调整模型参数,直至结果满意。
4.1 模型的建立
现以一个结构部件的数据为例,选取试验中M、Q、T与ε1、ε2、ε3的3组试验测量数据作为模型研究对象,每组试验数据220条,部分样本数据如表1所示。利用Python库的numpy pandas库进行数据处理和计算,利用sklearn分别建立随机森林、极端随机树、XGBoost、GBDT预测模型,将测试数据结构随机划分为两个部分,70%用于训练,30%用于验证集合。
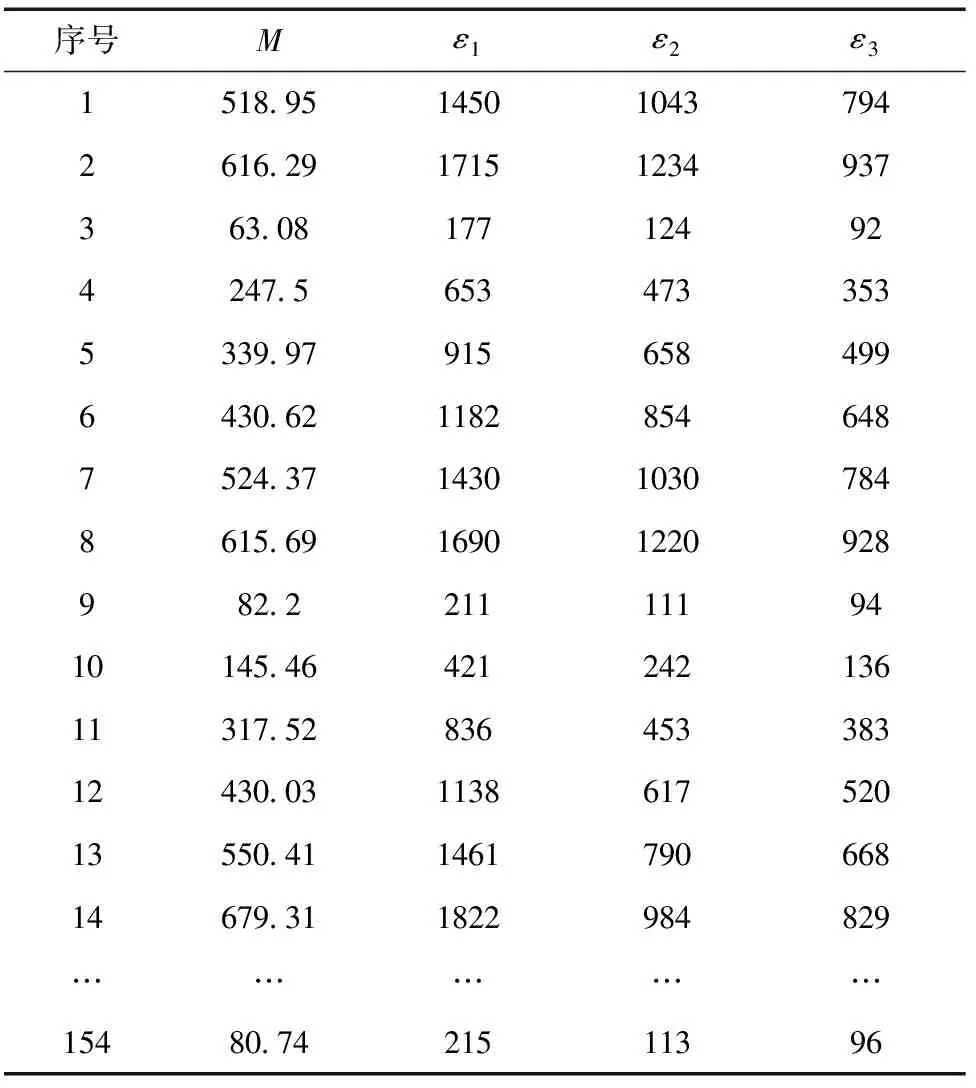
表1 部分样本数据
4.2 模型调参
模型调参是训练模型中不可缺少的,分别使用随机森林、极端随机树、GBDT、XGBoost等4种预测模型,模型的参数设置会直接影响模型的计算效率和精度。随机森林、极端随机树、XGBoost、GBDT预测模型都是基于决策树的算法模型,本文以决策树的数量n_estimators、最小样本数min_samples_split、最大深度max_depth、随机选择的最大特征max_features作为调参对象,进行反复计算比较。随机森林、极端随机树、GBDT、XGBoost模型参数如表2-表5所示。

表2 随机森林模型参数

表3 极端随机树模型参数

表4 GBDT模型参数

表5 XGBoost模型参数
4.3 模型的计算
根据上述模型和数据,使用Python编写程序进行计算,计算流程如图4所示。
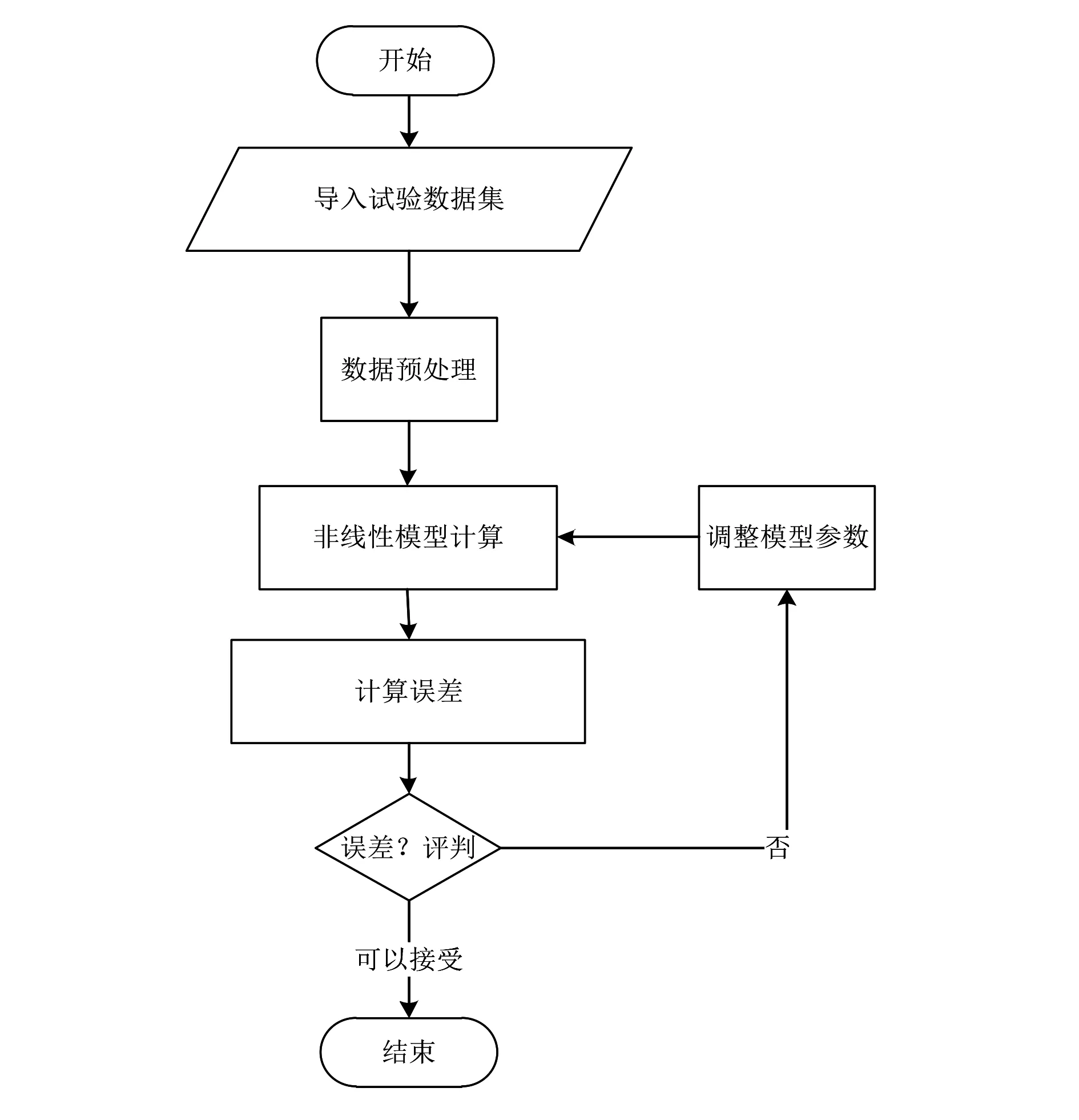
图4 非线性处理流程
(1)预处理,将标定试验数据汇总到一个文件中,对各参数的取值范围、趋势进行人工识别。
(2)选取随机森林、极端随机树、XGBoost、GBDT回归预测模型进行训练,验证误差情况。
(3)计算误差,误差在合理范围内流程结束,否则修正模型参数继续计算。
(4)输出结果。
按照以上流程进行训练,部分样本的训练集计算结果如表6所示。
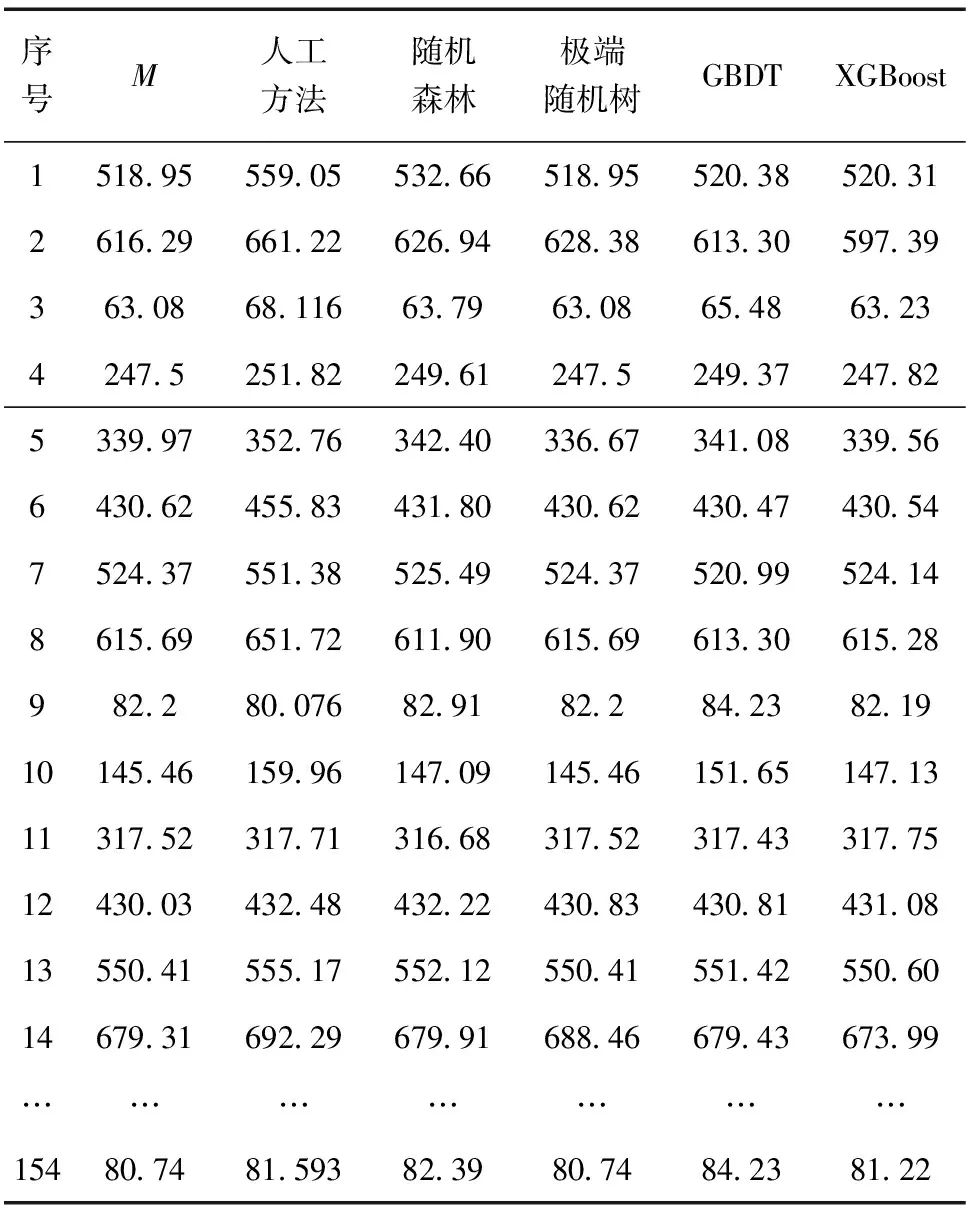
表6 部分训练集结果
4.4 计算结果的验证和评判
为了对非线性模型回归效果优劣做出判断,本文使用以下指标进行回归分析评判:模型训练时间;平均相对误差(Mean Absolute Percentage),记作MAPE,通常转为百分数进行比较;另一指标是确定系数,记作R-square。
(17)
(18)
对样本70%的数据分别进行4种模型的训练,同时统计模型的平均相对误差、确定系数、训练耗时,结果如表7所示。从计算结果可以看出,GBDT模型是最优的。
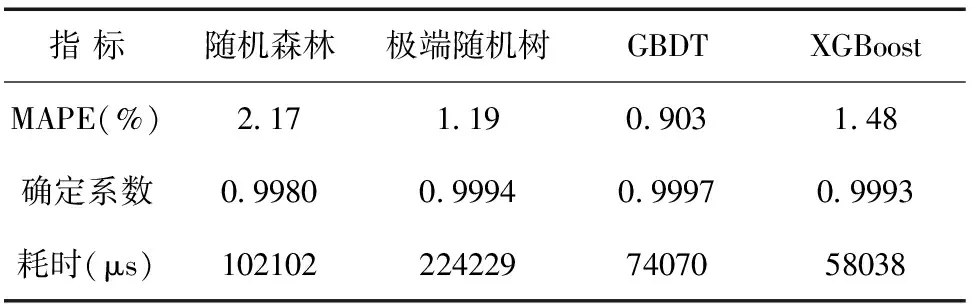
表7 模型指标计算
利用样本数据的30%的66个样本作为验证集,针对验证集的数据预测结果,计算相对误差百分比,部分数据计算结果如表8所示,表中的后5列分别是人工线性方法和4种非线性回归模型误差值比较。从表中结果可以看出,大部分的验证结果中非线性计算模型的精度高于人工线性模型的计算精度。同时,在4种非线性模型计算中,GBDT模型结果表现最好。
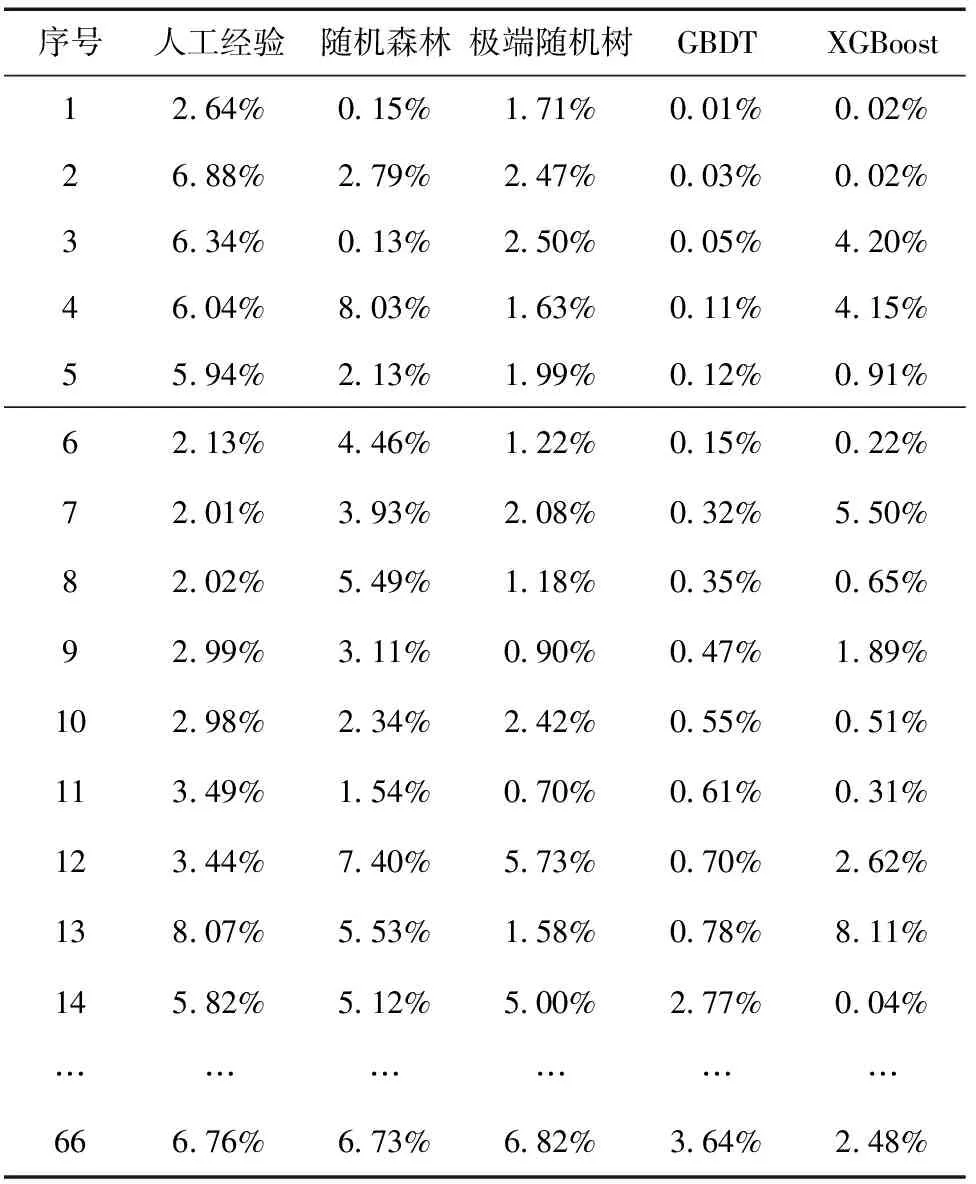
表8 部分验证集结果
对4种非线性模型的总体样本平均误差(包括测试集和验证集所有样本)、确定系数和计算耗时进行了比较。对相同测量部件的220个样本,用线性和非线性两类模型进行回归分析,对比多种模型下各样本点的残差,以此判断模型的优劣。综合各指标结果,验证了GBDT模型的优势。
5 非线性模型分析结果
图5、图6给出了人工方法和GBDT非线性预测值与真实值差异。从图中线条的走势可以看出,非线性预测结果好于人工线性方法的预测。从误差计算结果可以看出,非线性模型的总残差小于人工线性模型,且极端随机树和GBDT效果较优秀,说明非线性回归模型能较好地模拟样本数据。
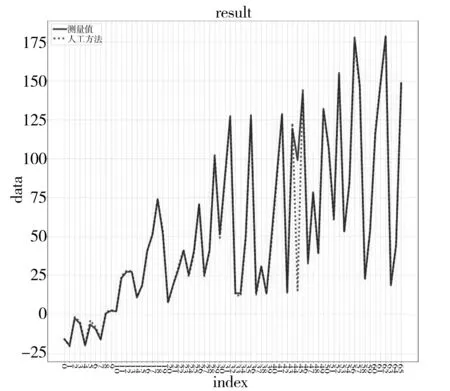
图5 人工方法预测数据
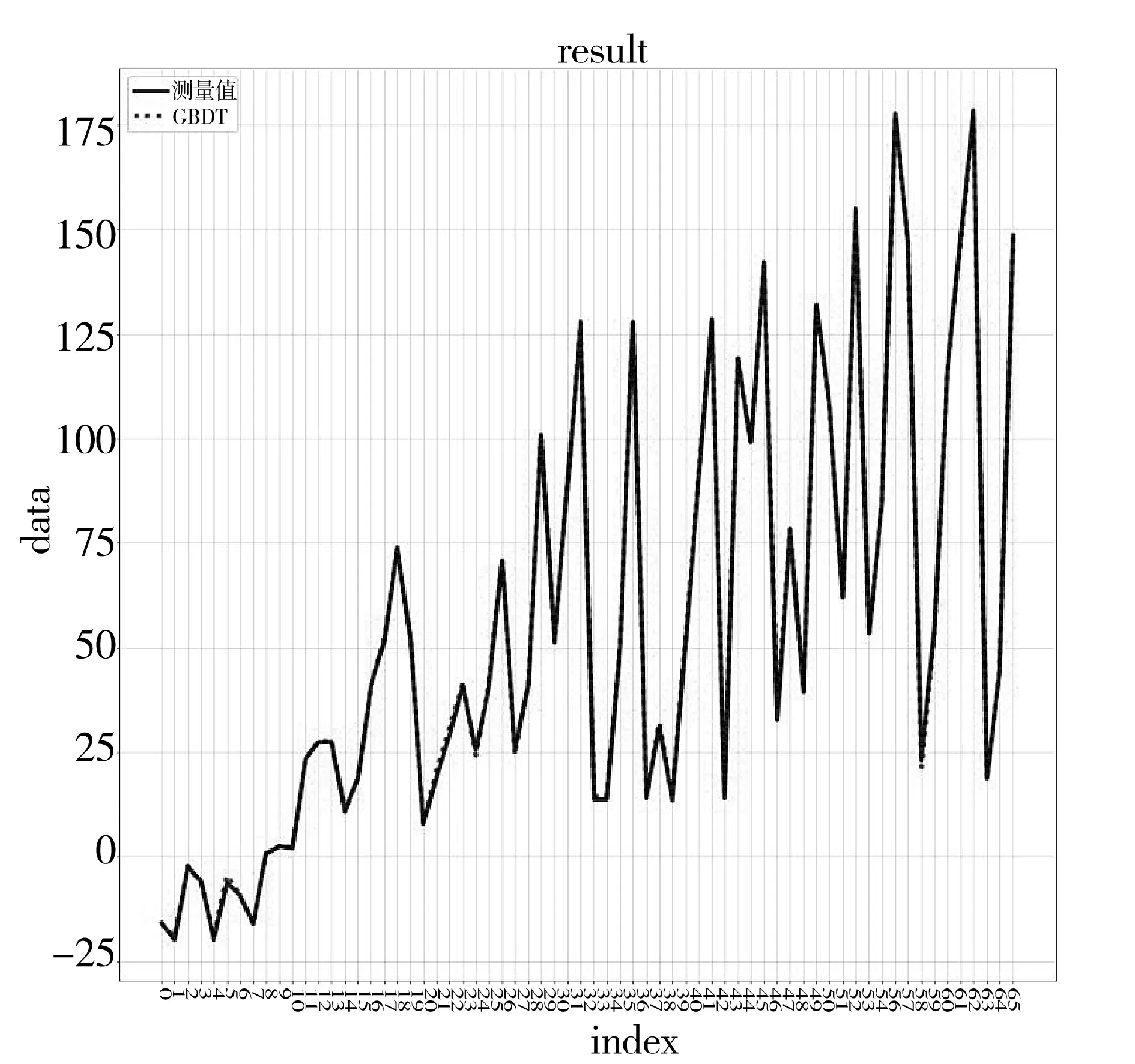
图6 GBDT预测数据
6 结 论
本文以某特定飞机结构部件的标定试验数据为研究对象,采用机器学习中基于决策树的4种算法(随机森林、极端随机树、GBDT、XGBoost)分别建立了回归预测模型,用可视化图表和相关指标进行了模型评价,得出以下结论:
(1)相比基于线性的模型算法,非线性模型能够识别相关特征变量之间的耦合关系,对于样本预测具有较高的准确度。对于本文中的数据样本,训练集误差可以控制到3%左右。
(2)在随机森林、极端随机树、GBDT、XGBoost这4种算法模型中,GBDT模型的精度是最优的,计算效率也较高。
