非接触检测技术在土木工程中的应用
2022-02-05孙立国江守燕杜成斌
孙立国,江守燕,杜成斌
(河海大学力学与材料学院,江苏 南京 210098)
1 引 言
基于多普勒效应制造的激光测振仪可对结构进行非接触测量,其与传统传感器相比,具有对结构附加影响小、受电磁干扰小、空间分辨率高和频响范围广等优点。激光测振仪在振动测量方面的优良表现,使其在越来越多的领域得到了应用,如模型模态参数识别、机械转子振动检测、结构损伤检测、医疗健康检测等[1-5]。由于激光测振仪具有便捷、快速、高效等特点,近来在土木工程领域也得到了广泛应用。黄智德等[6]采用激光测振仪和常规传感器对斜拉桥拉索进行测试,结果表明,激光测振仪同常规传感器测试结果具有良好的一致性。孙立国等[7-9]采用激光测振仪测试了厂房排架顶振动、厂房的网架及渡槽结构的模态参数,得到了较好的结果。肖浩东等[10]采用双激光测振仪研究了基点的选择对悬臂梁结构动参数的影响。
2 激光测振仪工作原理
激光测振仪[11,12]通过发射激光并探测其在物体上反射回来的多普勒频移,计算出被测物体相对于激光测振仪的相对运动速度。如图1所示,单束频率为f的激光通过分光镜,一部分直接投射到光电探测器上,一部分经过被测物体反射后再投射到光电探测器上,两组激光束混合在光电探测器上产生拍频信号[3,4],对其进行信号处理可得被测物体的振动速度时程。反射光的多普勒频移fD为:
(1)
式中,v为激光束照射区域物体的运动速度,λ为激光束的波长。

图1 单光束测速光路结构
3 典型工程应用
3.1 厂房排架柱顶位移振动测量

图2 测试原理
测试原理如图2所示,由于场地条件的限制无法在垂直排架和平行排架方向布置激光测振仪时,可以在任意的C、B两点同时架设激光测振仪,通过测量排架柱顶A点沿着测量路径AC和AB的振动,根据三角函数关系,计算出排架柱顶垂直轨道方向(X方向)和沿轨道方向(Y方向)的振动速度Vx和Vy。计算过程如下:
(2)
(3)
(4)
(5)
式中,V1、V2分别为AC和AB光路上的振动速度,x1、x2分别为垂直轨道方向测点C和测点B到排架的距离,y1、y2分别为平行轨道方向测点C和测点B到排架的距离。
图3为激光测振仪测量柱顶A点的振动过程,柱顶测点布置、柱顶振动测试现场见图3(a)、图3(b),图3(c)为测振仪所测光路上的振动时程,图3(d)为经过式(2)-式(5)计算后的柱顶振动时程。

(a)柱顶测点布置图

(b)柱顶振动测试现场

(c)柱顶A振动速度的时程典型曲线

(d)柱顶A振动位移的时程典型曲线图3 混凝土排架柱顶振动测试
3.2 系杆拱桥索力测试
由张紧弦理论可知,在测得吊杆的自振频率后,可根据下式计算出拉索的拉力。
(6)
式中,Fn为第n阶频率计算出的吊杆拉力,m为吊杆单位长度的质量,L为吊杆的长度,fn为吊杆的第n阶自振频率,n为所取自振频率的阶数。
吊杆长度的选取直接影响到吊杆拉力的计算结果。对于本桥的吊杆,由于在上、下锚头间分别有上、下减振圈,该减振圈会对吊杆的振动起约束作用。因此在计算吊杆拉力时,上式中的吊杆长度取吊杆上、下减振圈间的长度。吊杆索力测试如图4所示。

(a)索力测试现场

(b)激光测振仪吊杆振动信号图
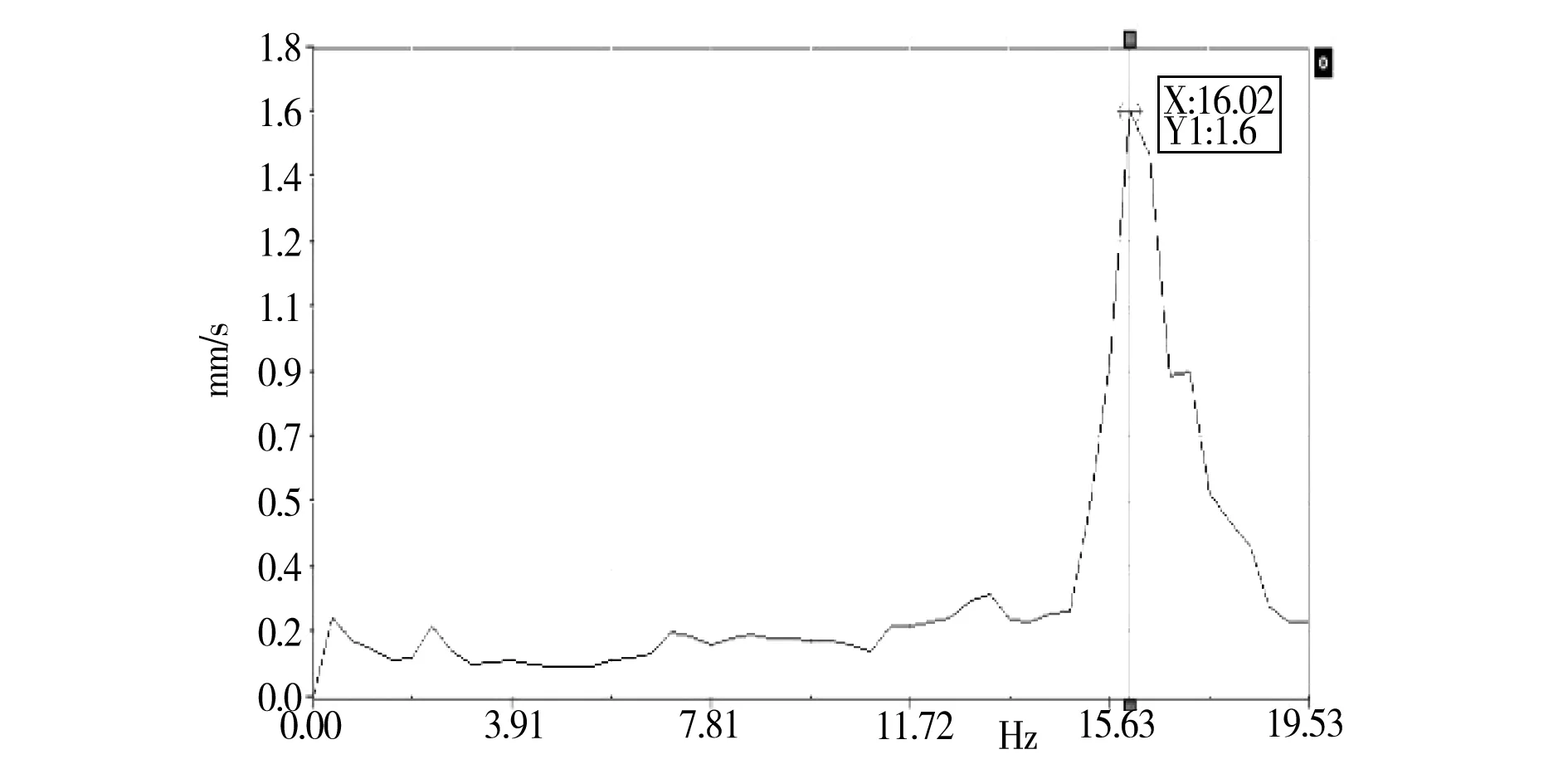
(c)激光测振仪振动信号频谱分析
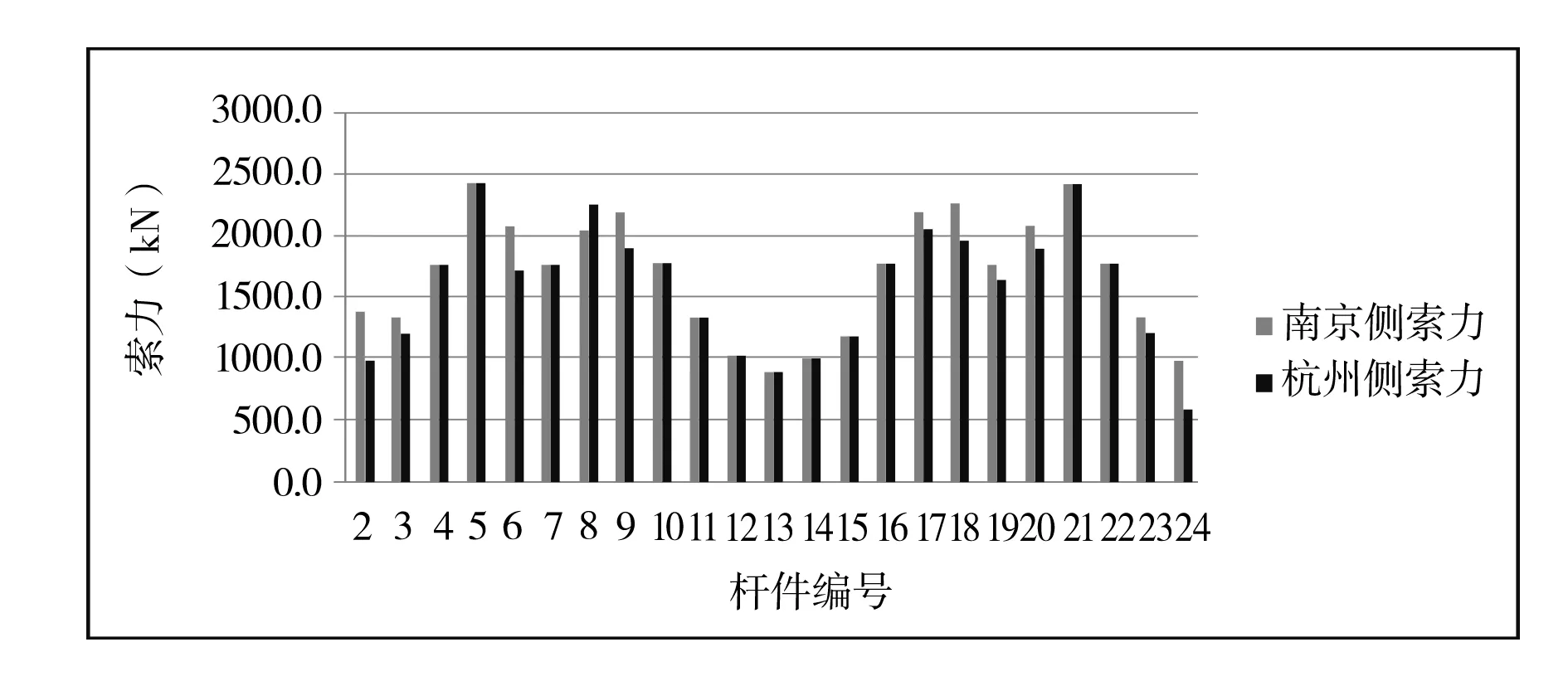
(d)两侧吊杆索力对比分布图图4 桥梁吊杆索力测试
3.3 电厂内机组、反应塔和烟囱振动相关性测量
相关分析是研究两个随机变量的线性关系,通常采用相关函数研究两随机函数x(t)和y(t)经过一段时间后的相似性。互相关函数Rxy(τ)表示两个随机过程{x(t)}和{y(t)}相关性的统计量,定义为:
(7)
其中,Rxy(τ)是延时τ的函数,反映了两个函数在不同相对位置上的匹配程度,峰值偏离原点的位置反映两个随机信号的时差。
Rxy(-τ)=Ryx(τ)
(8)
式(8)表明,两信号互换后对称于坐标轴,其中一个信号导前与另一信号滞后结果相等。
工程上常用互相关系数来表征两信号的相关性,公式如下:
(9)
式中,μx、μy和σx、σy为两随机函数x(t)和y(t)的均值和方差,互相关系数反映了两随机信号的相关性,可用于识别信号的传播途径、传播距离和传播速度。
利用多普勒激光测振仪测试振动信号,用烟囱顶部的噪声传感器测试噪声。分别对电机基础、出风机烟道、进烟囱烟道、钢烟囱结构等位置进行振动相关性测试。电厂内机组、反应塔和烟囱振动相关性测量如图5所示。测试结果表明,烟囱顶部噪声源主要来自引风机。
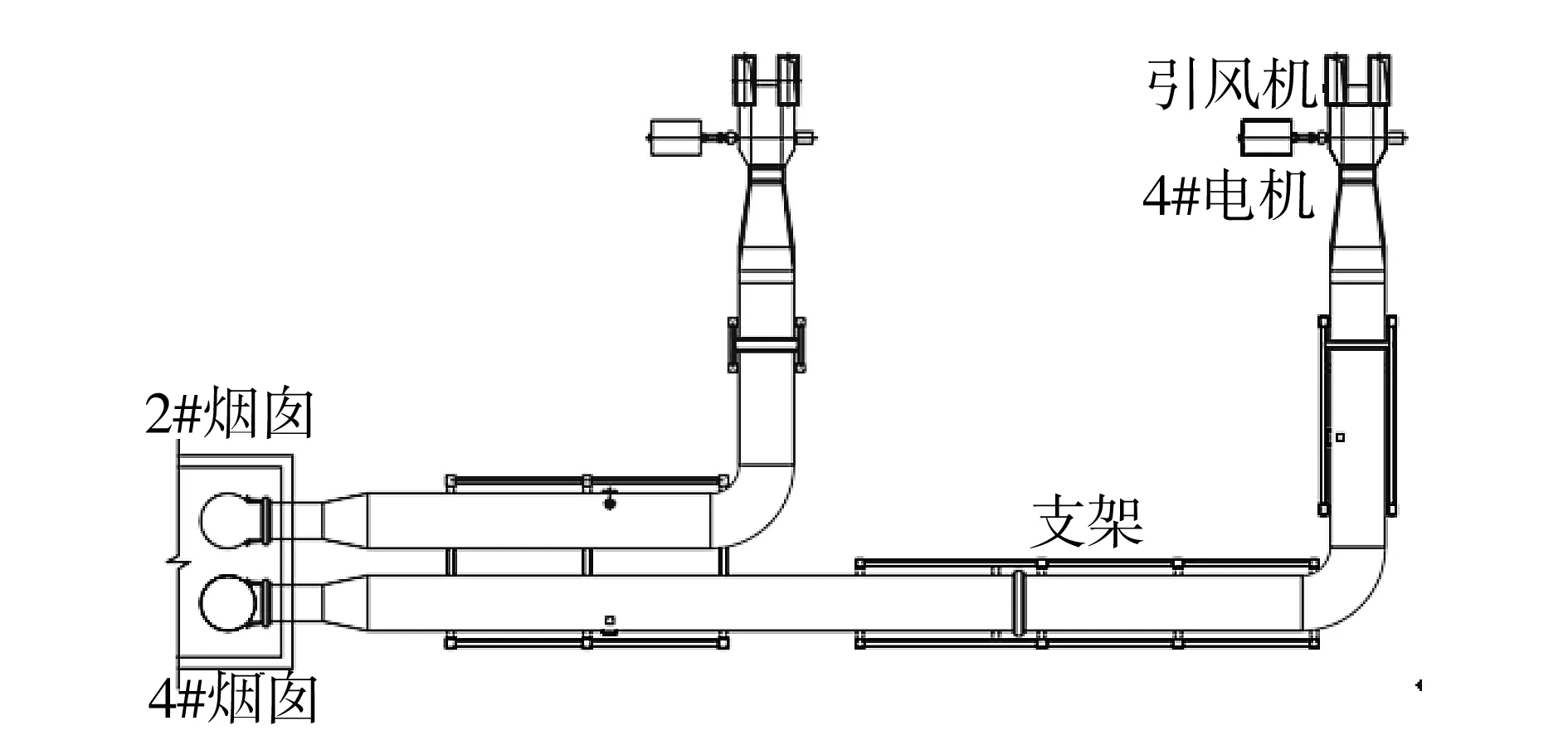
(a)相关性测试测点布置

(b)激光测振仪测量烟囱振动现场

(c)烟囱口噪声信号频谱分析

(d)烟囱口噪声与引风机振动相关性分布图图5 电厂内机组、反应塔和烟囱振动相关性测量
3.4 厂房网架的模态参数识别
Bendat等[13]认为,对于一个实模态的系统,其频响函数为:
(10)

结构上任意一点i的动态位移响应xi(ω),可以用k点激励力fk(ω)和结构频响函数Hik(ω)表示为:
(11)
假设将结构上某一点的输入响应作为参考点,则可通过其他测点和该点的响应相关性建立传递函数,进行结构系统的参数识别。传递率可表示为:
(12)
式中,序列αi(ω)可近似看作频率ω的模态振型。将式(11)代入式(12),可得:
(13)
将式(10)代入可以简单地写为:
(14)
上式中,由于点p作为参考点是固定的,因此对于一个有确定固有频率ωr处,φpr是一个定值,所以上式可以简化为:
(15)
上述理论表明,结构的模态参数可在不知道激励输入的情况下,根据测点之间的自、互功率谱,结合互谱相位、传递率等来估出。
根据以上理论,采用多普勒激光测振仪对厂房网架的7个位置进行振动测试,测点布置如图6所示。根据测试结果,网架的第一、二、三阶频率为3.88Hz、4.44Hz和5.62Hz,对应的阻尼比为2.43%、2.05%和1.98%。厂房网架测试测点布置、网架实物、网架模态参数测试现场见图6(a)-图6(c),网架的前三阶振型见图6(d)-图6(f)。

(a)厂房网架测试测点布置

(b)厂房网架实物图

(c)厂房网架模态参数测试现场
(d)网架识别的一阶振型图
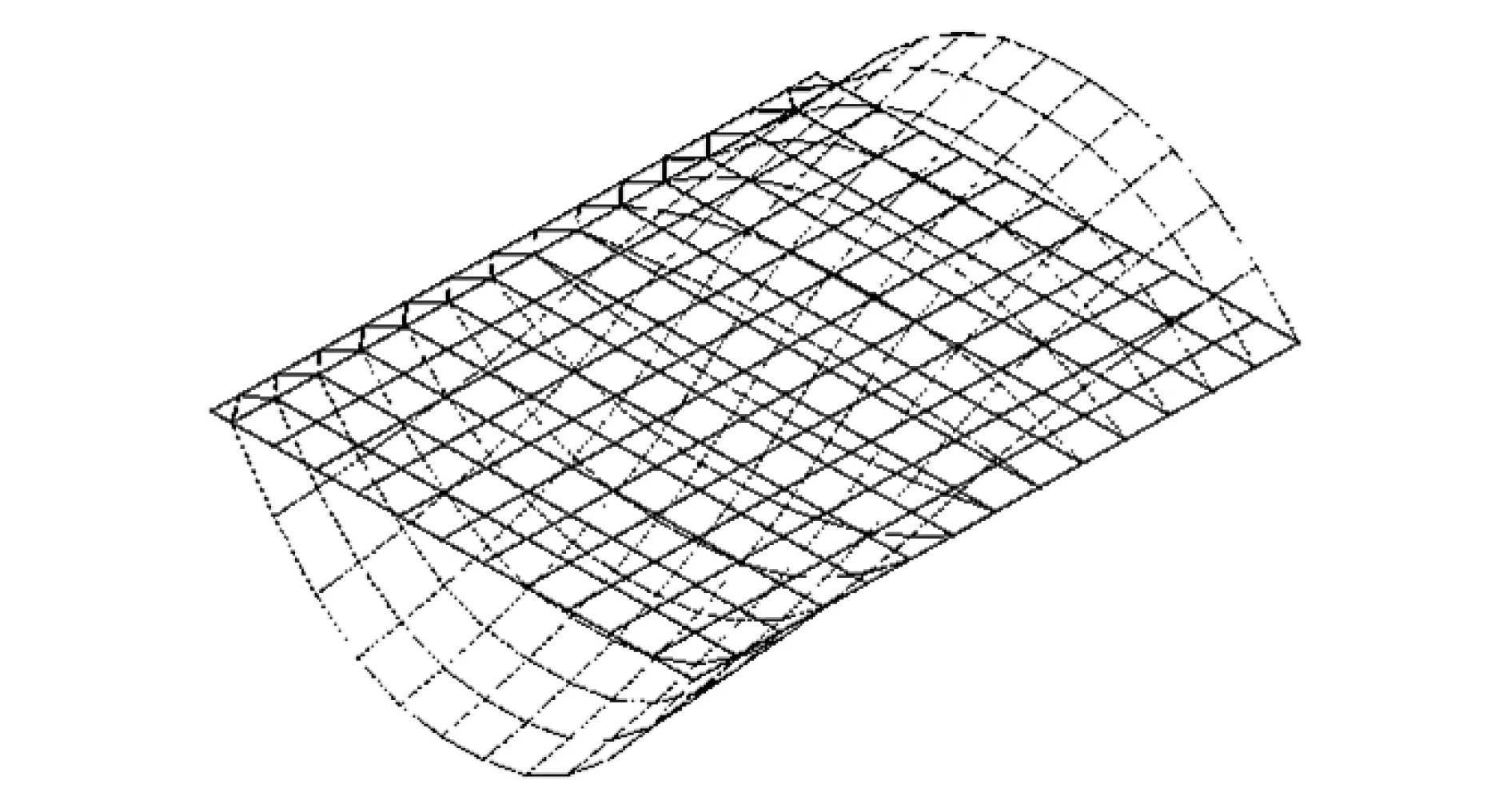
(e)网架识别的二阶振型图

(f)网架识别的三阶振型图图6 厂房网架模态参数识别
4 结 论
本文通过厂房中排架柱顶振动量,系杆拱桥结构中吊杆索力测量,垃圾焚烧电厂内机组、反应塔和烟囱振动相关性测量,厂房中网架的模态参数测量等4种典型振动测试类型的测试,探讨了激光测振仪在土木结构中振动测试的可行性。以上测试涵盖了单点振动量、单点振动频率、多点振动相关性以及结构整体模态参数识别4种振动测试方法。结果表明,采用非接触激光测振仪可方便、快捷和高效地完成土木结构中不同振动测试需求的测量。
