柱点支承螺栓球网架结构自重估算研究
2022-09-26王永,程建伟
0 引言
网架结构是指将杆件按照一定的规律通过节点连结而成的空间结构,具有空间受力小、重量轻、刚度大、抗震性能好等优点,便于工厂化生产和现场安装,常用于公共建筑和工业厂房的的屋盖(图1)。网架自重是网架结构自身的重量,对于螺栓球节点网架,网架的自重包含两部分:杆件自重、节点自重,网架杆件材料一般采用Q235B钢管,网架螺栓球节点由螺栓球、螺栓、螺钉、套筒等钢材零部件组成(图2)。网架自重估算对于网架结构选型以及预算控制均有着重要作用。现行行业规程《空间网格结构技术规程》(JGJ7-2010)中规定了自重可按照下面的计算公其中式中的gok-网架自重荷载标准值;qw-除网架自重以外的屋面荷载的标准值(kN/m2);L2-网架的短向跨度(m)。该自重估算公式是一个近似的经验公式,网架自重估算不准的影响较大,为确保网架结构的安全,有必要根据工程统计结果,对网架规程中自重估算公式的适用性进行分析与调整,保证估算的准确性。

图1 网架结构布置
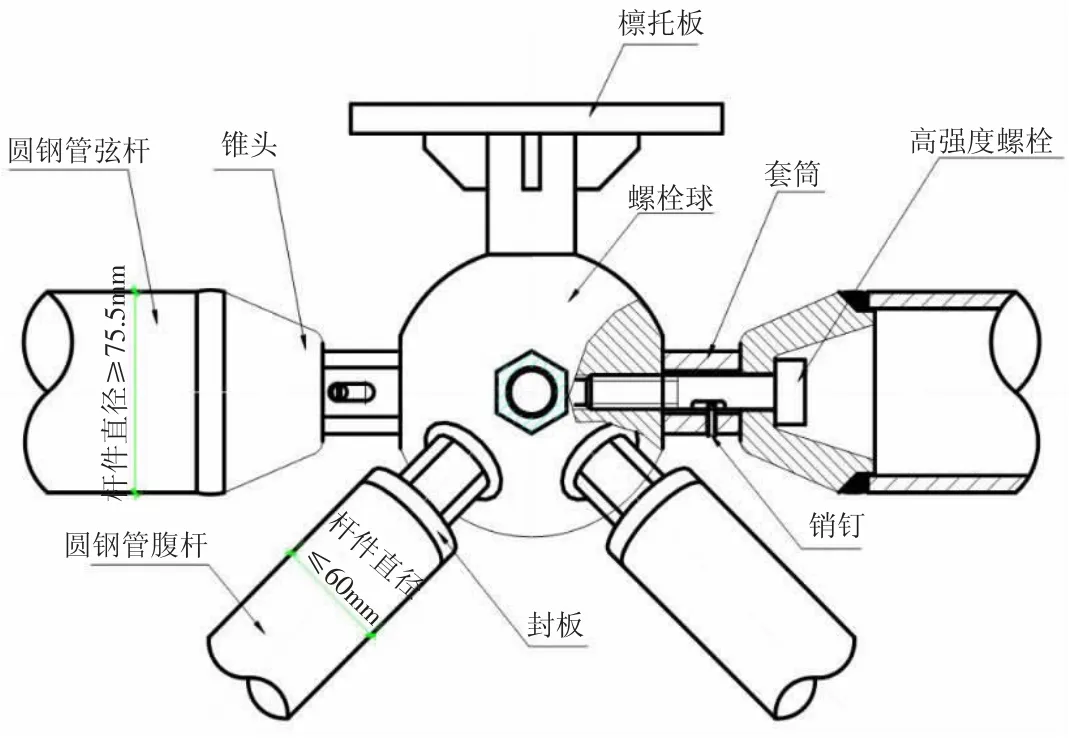
图2 螺栓球节点连接
查阅近年来国内的参考文献,关于网架自重研究的文献不多。有学者提出将自重估算公式中系数由1.0提到1.6的建议[1];也有学者分别对正放四角锥和斜放四角锥共计400个网架施工图进行了分析,经过统计和回归后得到了各级荷载作用下具有95%保证率的参数值以及参数值与短向跨度的关系曲线,在统计和回归分析的基础上,得出了网架自重估算的修正公式[2];还有学者以正放四角锥网架结构作为研究对象,分别考虑两种不同的结构自重进行建模并计算,将计算所得结果进行对比分析,得出采用定义材料密度并施加重力加速度在结构上的方式更偏于安全的结论[3]。
1 柱点支承网架结构自重计算公式适应性分析
1.1 网架自重及偏差数据分析
本文统计了16组柱点支承螺栓球节点网架的加工图数据,对网架自重进行汇总分析,计算出每个网架的自重实际值和按规范公式的估算值,对二者进行比较,统计结果见表1。
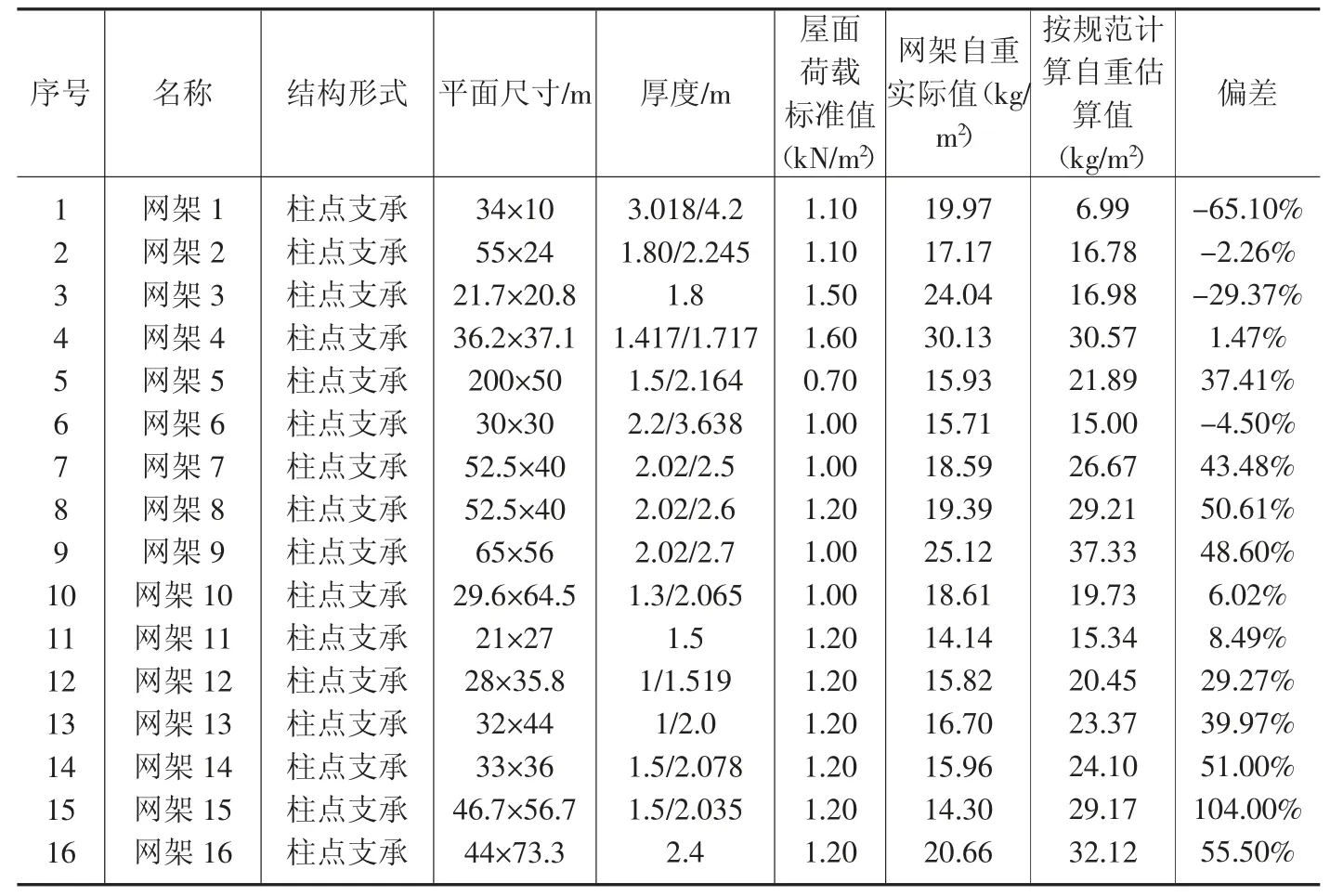
表1 柱点支承网架自重实际值及估算值
根据表1可知,按规范公式计算出来的网架自重值与网架自重实际值之间有以下两个特点,一是二者偏差较大,二是偏差有正有负。经统计分析,16个柱点支承网架中有5个偏差在±10%以内,有2个偏差在±30%以内,有4个偏差在±50%以内,有5个网架的偏差超过±50%,最大偏差甚至达到了104%。经计算,16组数据的自重偏离比平均值μ1=1.25,标准差σ1=0.41,变异系数ε1=0.33,数据离散性较大。
以上分析表明,根据规范公式得到的柱点支承网架自重估算值与实际值偏差较大,有必要对柱点支撑网架的自重估算公式开展进一步的修正。通过对网架自重估算公式进行修正,提高网架计算公式的精度和应用范围,也为相关规范的修订提供一定的参考依据。
1.2 网架估算自重与偏差关系分析
以样本数据的网架估算自重值为x轴,以估算值与实际值的偏差为y轴,可以得到网架自重估算值与偏差的散点图(图3),从图中可以得出以下规律:①随着网架自重估算值的增加,计算偏差由负值逐渐过渡到正值,即随着网架自重估算值增加,偏差呈现先减小后增大的趋势;②当估算自重值较小时,偏差为负值,意味着估算值比实际值要小,当估算自重值较大时,偏差为正值,意味着估算值比实际值要大;③对图中散点数据进行线性、对数、二次多项式、四次多项式拟合,四种拟合的R2值均在0.550~0.600之间,拟合效果一般。

图3 线性拟合结果
1.3 网架实际自重与偏差关系分析
以样本数据的网架实际自重值为x轴,以估算值与实际值的偏差为y轴,可以得到网架自重实际值与偏差的散点图(图4),从图中可以得出以下规律:①随着网架实际自重值的增加,计算偏差由正值逐渐过渡到负值,即随着网架自重实际值增加,而偏差呈现先减小后增大的趋势;②当实际自重值较小时,偏差为正值,意味着估算值比实际值要大,当实际自重值较大时,偏差为负值,意味着估算值比实际值要小;③对图中散点数据进行线性、对数、二次多项式、四次多项式拟合,四种拟合的R2值均在0.550左右,拟合效果一般。

图4 线性拟合结果
2 周边支承网架结构自重估算公式修正
2.1 修正前样本数据的处理
对表1的数据进行相应处理,得到表2。其中,面厚比m=网架展开面积/网架厚度,自重偏离比n=按规范计算自重值/实际自重值,m和n均为无量纲单位。显然,自重偏离比越接近1,说明估算值越准确。

表2 周边支承网架自重有关数据
2.2 考虑面厚比进行修正
网架自重除受荷载大小、支承形式、跨度大小等因素有关外,还与网架厚度、网格尺寸等因素有关,为综合考虑网架厚度与跨度的影响,以面厚比为x轴,以自重偏离比为y轴,绘制散点图,见图5。对数据分别进行线性、指数、对数、多项式、幂函数拟合,拟合结果显示采用幂函数拟合结果略优,拟合后的R2=0.610。根据拟合结果,可以得出修正系数k=0.044m0.5(m为面厚比)。
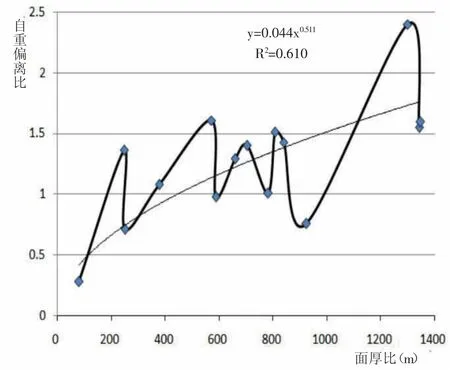
图5 自重估算值与自重偏离比关系图
表3中计算出16组数据在考虑修正系数k之后的n/k值和修正后估算值,修正后自重偏离比见图6。
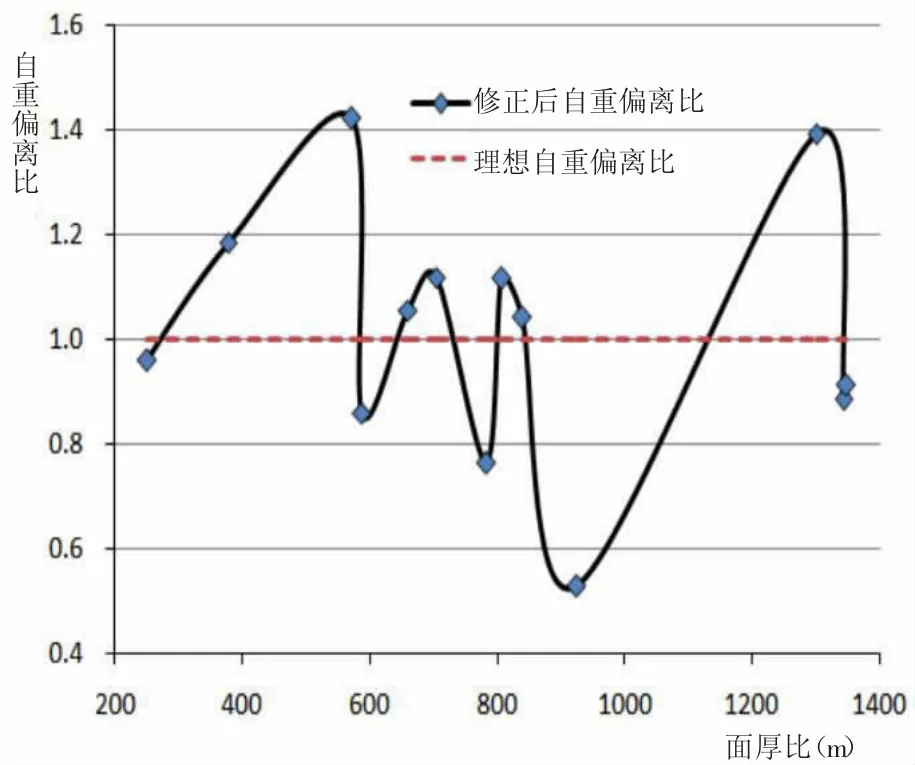
图6 修正后自重偏离比
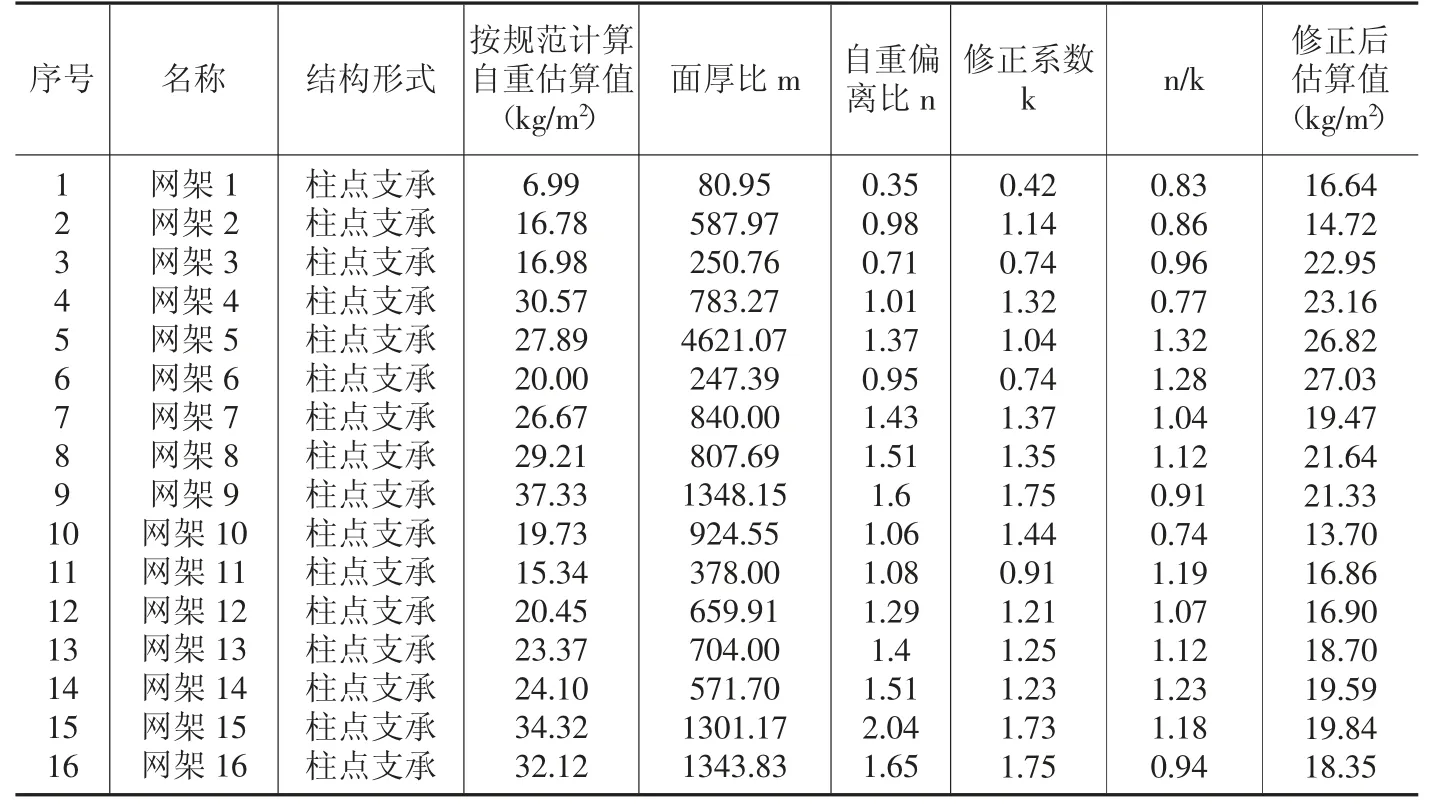
表3 自重修正后数据
根据修正后的结果,修正后的自重偏离比n/k的平均值μ2=1.04,标准差σ2=0.19,变异系数ε2=0.18。对比原自重偏离比,数据的平均值有了显著提高,数据的离散程度也有明显改善。
2.3 修正系数的确定与应用
除了上述面厚比修正方式外,还针对自重估算值、长短跨比等参数进行修正。经比较,按面厚比进行修正结果相对较为理想一些,其它几种修正方式也能起到一定的作用,但是数据的离散性仍然比较大。因此,建议按面厚比进行修正。
结合规程给定的计算公式,修正后的周边支承网架自重计算公式为
其中式中的gok-网架自重荷载标准值;qw-除网架自重以外的屋面荷载标准值(kN/m2);L2-网架的短向跨度(m);修正系数k=0.044m0.5(m为面厚比)。
3 结论
通过以上研究和分析,可以得出以下结论:
①对周边支承网架,按规范公式计算出来的网架自重荷载标准值与网架自重实际值之间偏差较大,有必要对规范给定公式进行修正。
②参考规程给定的计算公式,修正后的周边支承网架自重计算公式为:
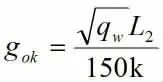
式中:gok-修正后网架自重荷载标准值;qw-除网架自重以外的屋面荷载标准值(kN/m2);L2-网架的短向跨度(m);修正系数k=0.044m0.5(m为面厚比)。
③对周边支承网架自重估算修正系数进行了研究,相比较原自重偏离比,估算精度明显提高,修正后的自重估算值较接近实际值,估算数据的离散程度也得到了明显改善。
