可调焦双稳系统随机共振特性及应用研究*
2022-02-04黄玉杨黄咏梅
黄玉杨,黄咏梅,林 敏
(中国计量大学计量测试工程学院,浙江 杭州 310018)
近年来,非线性科学不断发展,随机共振理论为强噪声背景下微弱信号检测提供了新方法。但是,随机共振需要信号、噪声和系统三者协同作用才能产生[1]。为了使随机共振能更好地应用于工程实际信号处理,人们相继提出了二次采样[2]、双调制[3]、尺度变换[4]、参数调节[5]等方法,应用于旋转机械故障检测[6]、低浓度气体检测[7]、液体成分检测[8]、图像增强[9]等领域。
经典双稳势函数是目前应用最为广泛的势函数,针对势函数存在的饱和特性,赵文礼等提出了不同类型的分段势函数,以双稳势函数的势阱底或势垒顶位置作为分段点,每段函数分别采用一次函数[10-11]、二次函数[12]、指数函数[13]等形式。这些势函数通过改变经典双稳势函数外侧的非线性形式来影响饱和特性和输出信号的幅值大小。但随机共振效应的强弱并非由输出信号的幅值大小决定,而是由系统的非线性与噪声相互作用产生的输出信号信噪比大小决定。因此,需要考虑无序的噪声与势函数作用产生的能量聚集,而具有焦点的抛物线型势函数则有着能量聚集的特性。
为增强随机共振效应,提高系统能量聚集能力,构建一外侧曲线为抛物线的势函数,通过调节抛物线焦距,改变系统非线性特性,特别是能量的聚集能力,建立焦距与Kramers 逃逸率和输出信噪比的解析式,分析了焦距对系统的饱和特性以及随机共振效应的影响,通过焦距的调节可以控制微弱信号和噪声相互作用,提高系统输出信噪比。
将该系统用于涡街流量计信号处理,以输出信噪比作为衡量指标,通过遗传算法自适应调节焦距等参数,提高小流量涡街信号的输出信噪比,准确获取涡街信号频率。
1 可调焦双稳势函数
受到周期信号S(t)与噪声N(t)作用的双稳系统可以由Langevin 方程描述:
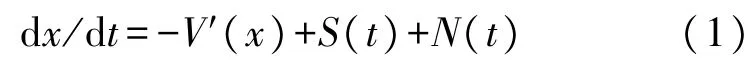
式中,S(t)=A0cos(2πf0t)为输入的周期信号,其中A0为信号幅值,f0为信号频率;N(t)为高斯白噪声;经典双稳势函数V(x)如式(2):
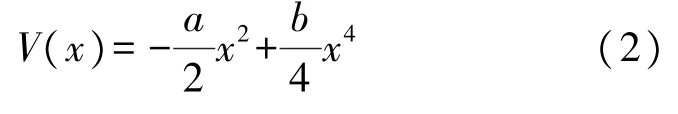
式中,a、b为势函数的参数,经典双稳势函数有两个稳定点,位置为,分别对应两势阱底部的位置,势阱宽度,有一个不稳定点,位置为xn=0,势垒高度h=a2/4b。
当x较大时,势函数V(x)中x的四次方项起主要作用,x的微小增加使势能快速增大。因此在经典双稳系统中,当输出信号幅值到达一定程度时,系统出现饱和现象。
构建可调焦双稳势函数U(x)可用式(3)表示,当a=1、b=1、P=1 时,对应的曲线如图1 所示。
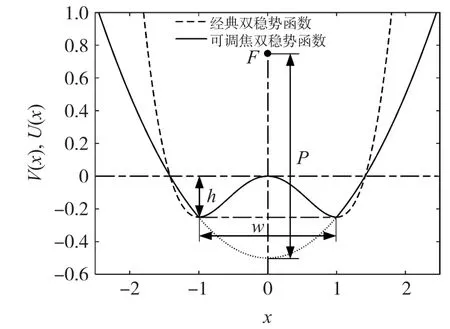
图1 可调焦双稳势函数曲线
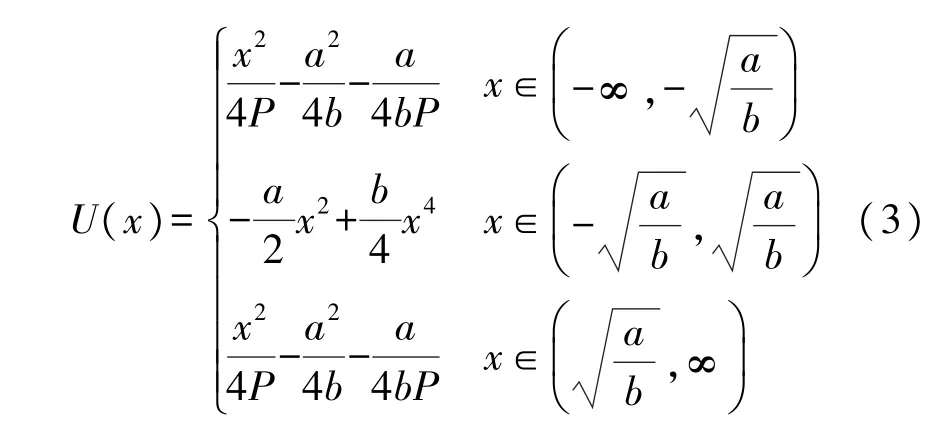
该势函数以经典双稳势函数两稳定点为分界点,外侧为抛物线,其焦距为P,大小可调,内侧保持原经典双稳势函数形式,将经典双稳势函数外侧的势能与位移之间的四次方关系转换为二次方关系。势函数外侧对应抛物线顶点位置为(0,-a2/4ba4bP),焦点F位置为(0,P-a2/4b-a4bP)。当焦距P分别为1、2、3 时,对应势函数曲线如图2 所示。焦距P增大,抛物线焦点向上移动,势函数外侧开度增大,焦距P减小,则反之,当焦距P过大时,势函数外侧趋于水平,不具有双稳结构。可见,调节焦距P的大小可直接改变抛物线形状,从而改变系统的非线性形式,进而改变信号、噪声与系统的协同作用及能量的聚集。
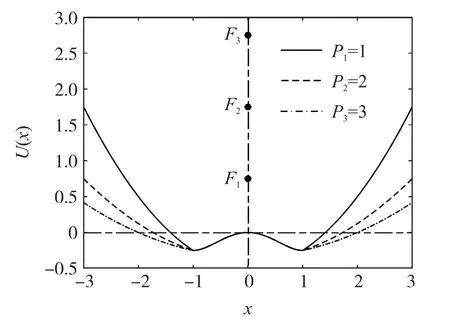
图2 不同焦距下可调焦双稳系统势函数曲线
2 焦距大小与随机共振效应
2.1 Kramers 逃逸率
双稳态系统在两个稳态间发生跃迁的速度,即为Kramers 逃逸率R。不同势函数的Kramers 逃逸率不同,因此系统对微弱周期信号的响应速率不同。Kramers 逃逸率越大,非线性系统能检测的周期信号频率范围越宽[14]。
从右势阱底部出发的布朗粒子Kramers 逃逸率如式(4):

积分简化计算可得式(5):
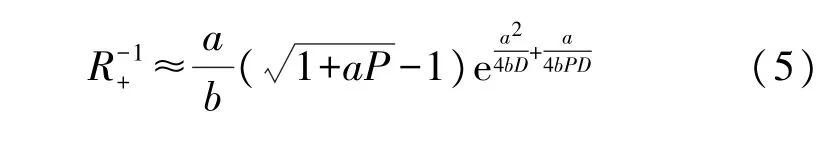
同理从左势阱底部出发的布朗粒子Kramers 逃逸率如式(6):
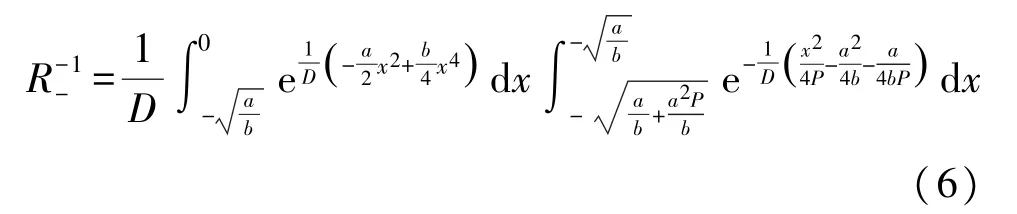
积分简化计算可得式(7):

因此,可调焦双稳势函数的Kramers 逃逸率R如式(8):

由式(8)可知,Kramers 逃逸率与焦距P密切相关。调节势函数焦距的大小,可以改变Kramers 逃逸率。
参数a=1、b=1,当焦距P=3,可调焦双稳势函数及经典双稳势函数的Kramers 逃逸率随噪声强度变化曲线如图3 所示,可调焦双稳系统的Kramers逃逸率明显大于经典双稳系统的Kramers 逃逸率,可调焦双稳系统可以更好地与信号、噪声匹配,扩大信号频率的检测范围。
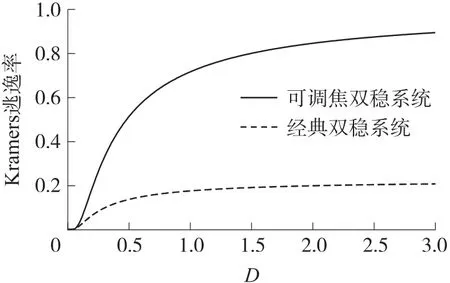
图3 Kramers 逃逸率随噪声强度变化曲线
2.2 输出信噪比
输出信噪比SNR 是衡量随机共振效应的重要参数。输出信噪比SNR 计算式如式(9)所示。
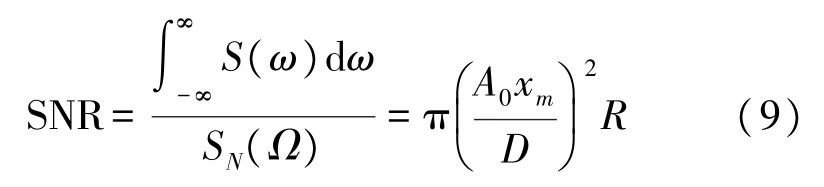
式中,S(ω)为信号的功率谱密度,SN(Ω)为噪声平均功率,将式(8)代入式(9)中,可得式(10):
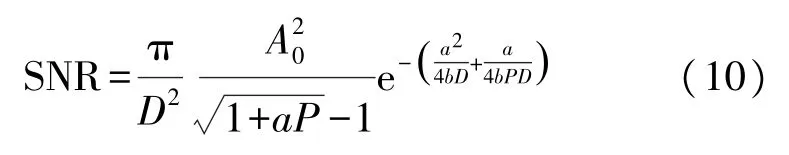
当信号幅值A0=0.05,焦距P=3,可调焦双稳势函数及经典双稳势函数的系统输出信噪比随噪声强度变化曲线如图4 所示,可见,随着噪声强度的变化,系统输出信噪比呈现明显的单峰曲线,且可调焦双稳系统的输出信噪比明显大于经典双稳系统的输出信噪比,说明可调焦双稳系统能提高对噪声无序能量的利用率,将更多的噪声能量转移至有序的信号中。

图4 输出信噪比随噪声强度变化理论曲线
当信号频率f0=0.01 Hz,信号幅值A0=0.05,噪声强度D=0.2,可调焦双稳系统的输出信噪比SNR随焦距P变化理论及仿真曲线如图5 所示。理论与仿真曲线趋势基本一致,随着焦距P的变化,输出信噪比呈现先增大后减小的单峰趋势,表明存在一个使信噪比值最大的焦距P,能够有效聚集能量,使非线性系统与信号、噪声更好地匹配,从而增强系统的随机共振效应。
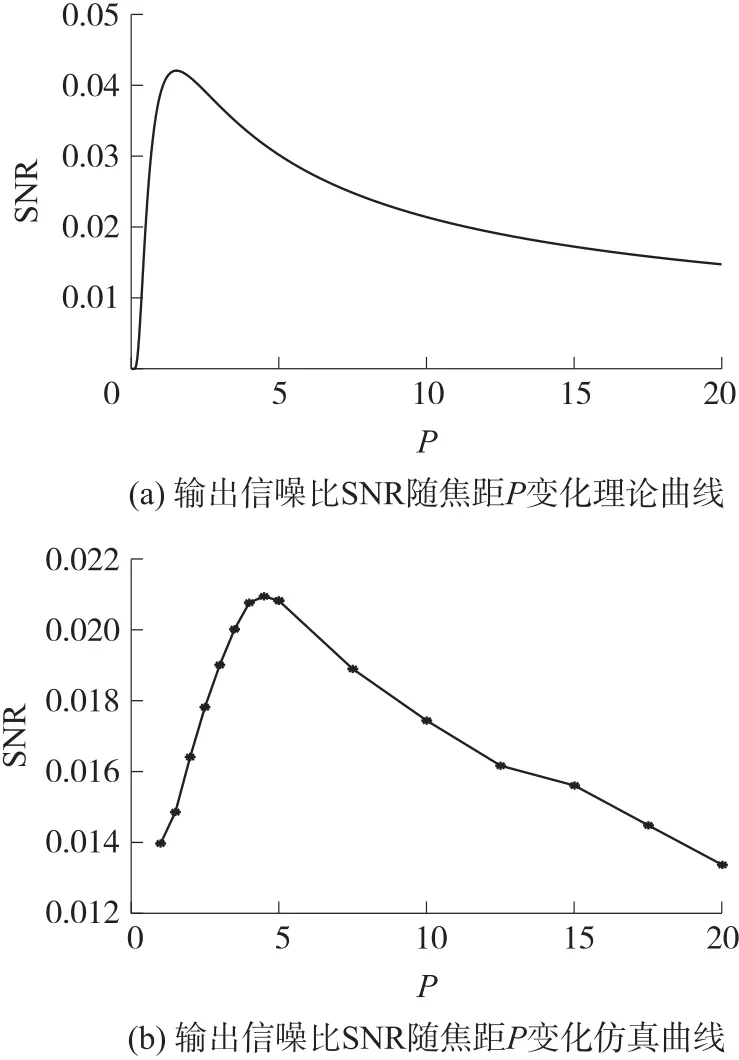
图5 输出信噪比SNR 随焦距P 变化曲线
系统输出信噪比的理论分析和数值仿真结果表明,调节焦距P的大小能影响系统能量的迁移,且存在最优的焦距P使得信噪比达到最大。
2.3 饱和特性的分析
当输入信号幅值A0分别为0.5,0.75,1.0,1.25,输入信号频率f0=0.01 Hz,噪声强度D=0,焦距P=3时,不同势函数下系统输出信号时域图如图6 所示。从图中可以看出,增大输入信号幅值,对于经典双稳系统,输出信号的幅值基本不变,系统出现饱和现象,而可调焦双稳系统的输出幅值则随着输入的增加而增加,且输出信号幅值大于经典双稳系统。
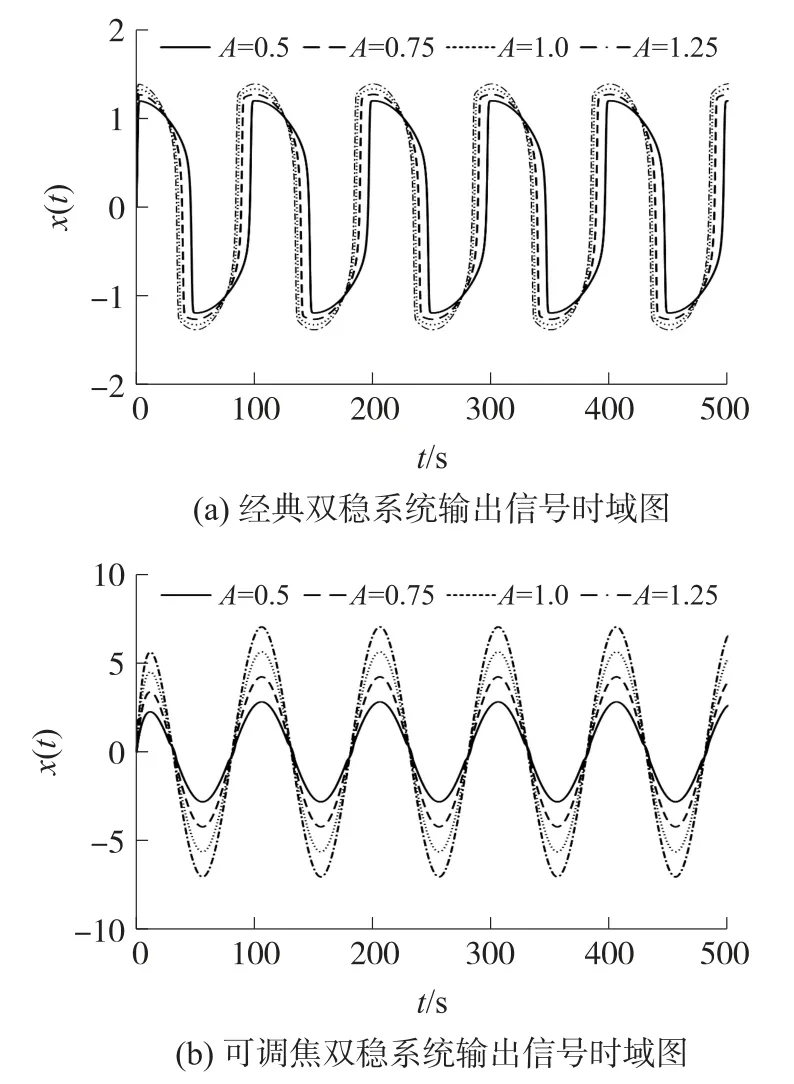
图6 经典双稳系统与可调焦双稳系统输出信号时域图
3 基于遗传算法的参数寻优及涡街信号处理
随机共振效应与势函数焦距密切相关,不同焦距具有不同的随机共振效应,获取最优焦距是随机共振能否成功应用于工程信号处理的关键。遗传算法是通过模拟达尔文进化论中优胜劣汰的规则自适应搜索最优解的方法,可进行多参数寻优,因此在应用于实际涡街信号处理中,通过遗传算法对参数进行寻优。
3.1 涡街信号特点及信号预处理
涡街流量计是近几年来发展较快的流量计之一,大多通过压电传感器测量漩涡压力的周期变化得到管道中流体流速。在工业现场使用时,涡街信号容易受现场噪声干扰,因此输出信号由周期涡街信号及现场噪声信号两部分叠加而成,在小流量测量时,涡街信号容易被噪声淹没。涡街信号频率f0与管道内流体流速Uv成正比[15],旋涡频率f0如式(11)所示:

式中,Sr为斯特劳哈尔数,d为旋涡发生体迎流面宽度,m为管道系数,在测量过程中,这些参数均为常数。
输出信号幅值与旋涡升力对应,与管道内流体流速Uv成二次方关系,旋涡升力FL如式(12)所示:

式中,CL为涡街流量计升力系数,ρ为管道内流体密度。
当信号和噪声作用于随机共振系统,根据绝热近似理论,在小参数条件下才有可能产生随机共振,因此涡街信号直接输入系统,并不一定与系统参数匹配,信号输入系统前需要对信号进行预处理,对频率进行调制,对幅值进行归一化。
二语学习负动机现象是非英语专业大学生群体中较为普遍且难以解决的问题。本研究采用问卷调查的方式对非英语专业大学生的负动机现象进行实证研究,发现导致动机减弱的影响因素主要与学习者、学习环境和社会因素相关,在此基础上还提出了有效的动机自我调控策略,无论是对二语教师的生态化教学还是对二语学习者的有效二语学习都将起到积极的促进作用。
信号频率调制如式(13)所示:

式中,S(t)为涡街流量计输出信号,信号幅值为A0,N(t)为信号中叠加的噪声信号,W(t)为调制信号,fc为调制信号频率,信号调制后得到输出信号S1、S2及S3,其中S1的信号频率Δf=f0-fc,调制信号频率fc越接近被检信号频率f0,输入到随机共振系统的信号频率越小,系统越容易产生随机共振,S2和S3输出相比S1非常微弱,可以忽略。
涡街流量计管道内介质流速大小不同,信号幅值会有较大变化,因此信号输入随机共振系统前对涡街信号进行归一化处理,如式(14)所示:

式中,X′为归一化处理后信号,X为原始涡街信号,Xˉ为原始涡街信号均值,δ为涡街信号标准差。
3.2 遗传算法检测步骤
输出信号信噪比SNR 直接反应了随机共振的强弱,因此以SNR 作为适应度函数筛选种群中的优劣个体。势函数焦距P直接影响系统非线性,选取合适的P可利用更多噪声能量,转移至输出信号中,增强输出信噪比;调制信号的调制频率越接近涡街信号频率,越容易产生随机共振,通过f0=fc+Δf,可以得到被检信号频率。因此使用遗传算法对焦距P及调制信号频率fc进行自适应寻优。图7 为遗传算法自适应寻优的流程图。

图7 遗传算法寻优流程图
具体步骤如下:
对焦距P及调制信号频率fc同时寻优,将两参数对应的二进制编码组成编码长度为l的染色体。编码长度分别设置为l1、l2,将其转换为{al2+l1al2+l1-1…al1al1-1…a2a1}的染色体,待优化变量的区间为[xmin,xmax],染色体可解码还原,调制信号频率fc的编码长度设置为16,焦距P的编码长度设置为8;
②种群初始化
随机生成染色体,组成确定规模的初始种群。将种群规模N设置为100,进化代数M设置为40;
③遗传、交叉与变异
计算个体适应度,选择出优良参数串数据个体。进行染色体交叉及变异。将交叉概率设置为0.6,变异概率设置为0.05;
④终止
重复步骤③,判断是否达到终止规则,若最佳适应度在M代没有明显变化,则视为收敛,输出该种群中的最佳染色体,终止搜索,否则继续迭代。
4 实验结果与分析
4.1 实验装置
搭建涡街流量计实验装置如图8 所示,通过工作量器给出标准体积。实验装置中涡街流量计精度为1.0,管道口径为50 mm,流量计管道内发生体迎流面宽度为14 mm,该流量计的量程为60 m3/h,斯特劳哈尔数经实验标定后为0.167 0。
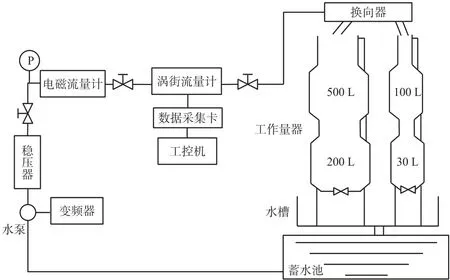
图8 涡街流量计实验装置示意图
4.2 数据处理与分析
选取小流量涡街信号进行实验分析。信号采样频率为200 Hz,当流量为7.16 m3/h 时,采集到的涡街信号时域图及频域图如图9 所示,图9(b)中信号功率谱峰值非常微弱。调制信号频率fc的搜索范围设置为[17,27]Hz,焦距P的搜索范围设置为[0,20],进行遗传算法自适应寻优,得到最优调制信号频率fc为18.396 6 Hz,最优焦距P为8.870 6,对应系统输出时域及频域图如图10 所示。从可调焦双稳系统输出时域图中看出,涡街信号产生明显周期性,从频域图中看出,信号的功率谱峰值明显增强,产生随机共振,产生共振时的差频Δf=0.002 3 Hz,该管道内流量的信号频率f0=fc+Δf=18.398 9 Hz,计算可得流量为7.12 m3/h,误差为0.70%。实验结果表明,通过可调焦双稳系统产生的随机共振能准确获取涡街信号频率。
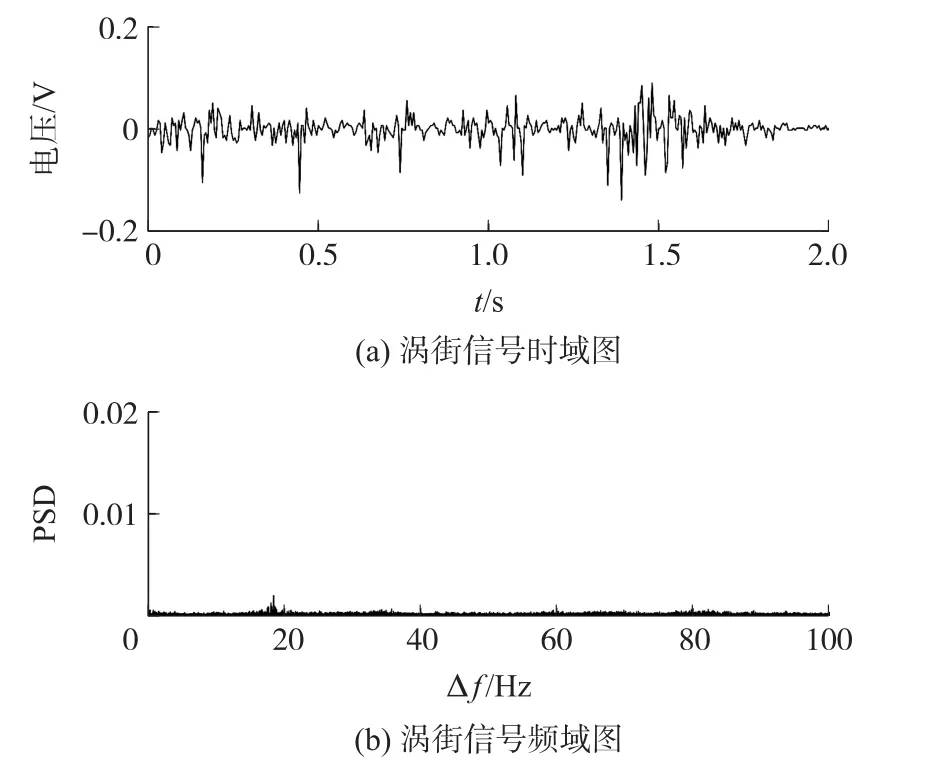
图9 小流量涡街信号时域图及频域图
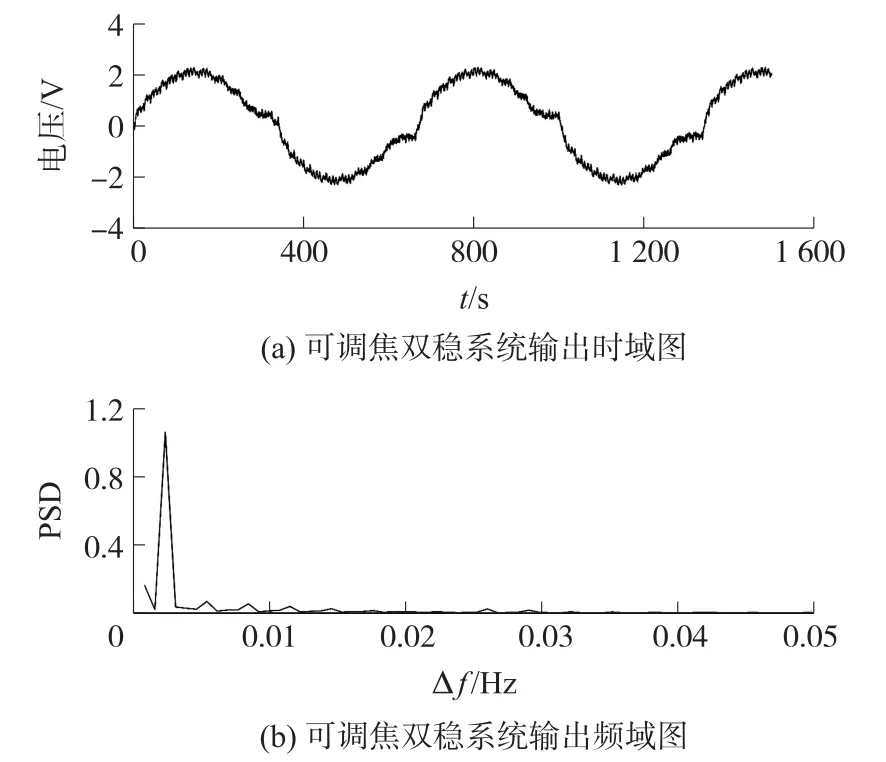
图10 可调焦双稳系统输出时域图及频域图
5 结论
随机共振效应与势函数形式及其参数有关,采用可调焦距的抛物线代替了经典双稳势函数两外侧的曲线,构建了一种新的可调焦双稳势函数,建立了势函数焦距P与系统Kramers 逃逸率和输出信噪比的近似解析关系,理论分析与数值仿真结果表明,调节焦距P可改变系统非线性特性,并且存在最优的焦距P能有效聚集能量,使输出信噪比最大,随机共振效应最为强烈。与经典双稳势函数相比,可调焦双稳势函数的随机共振效应更强。将该系统应用于涡街信号处理,通过遗传算法对势函数焦距P等参数进行寻优。实验结果表明,可调焦双稳系统产生较强的随机共振,能准确获得小流量涡街信号频率,具有较好的工程应用前景。
