基于有限元筒-锥结构外压计算长度当量方法的研究

叶凌伟 汪 斌 刘会彬

（浙江省特种设备科学研究院 浙江省特种设备安全检测技术研究重点实验室）

目前， 各标准中关于外压容器计算长度的规则存在差异［1］，特别是当锥壳的大端或小端不起支撑作用时，计算长度该如何取，锥壳厚度、筒体厚度该如何确定， 相对应的加强圈该如何设计等问题还需要进一步研究以得到更令人满意的结果。 ASME Ⅷ-1［2］标准中筒-锥结构不连续处的最小加强面积计算方法来源为Farr的理论分析，并未考虑锥壳可能起到的加强作用， 而EN 13445-3则将锥壳半锥角α≥30°的筒-锥结构不连续处作支撑线处理。 受外压筒-锥结构的设计思路为：首先考虑筒-锥结构连接处是否作支撑线处理，当作支撑线处理时，圆筒和锥壳分开设计；不作支撑线处理时，ASME Ⅷ-1、GB 150—2011［3］的常规设计将筒-锥壳的轴向长度作为外压计算长度。 对于受外压单一锥壳，其稳定问题较圆筒更加复杂，各个压力容器标准通常将锥壳当量成圆筒来设计。 基于ASME Ⅷ-1中锥壳的当量规则，结合EN 13445-3外压计算长度的规定， 笔者研究外压筒-锥结构计算长度和当量方法， 提出保守可行的当量方法， 改进了筒-锥结构的外压长度计算方法， 为工程实际问题和进一步关于筒-锥结构加强圈的设计提供参考。

1 外压容器计算长度概述

外压容器的计算长度对许用外压值影响很大。从理论上说，计算长度的选取应是判断在该容器长度的两端能否保持足够的约束， 使其真正能起支撑线的作用， 从而在圆筒失稳时仍能保持圆形，不致被压塌［4］。 对一台实际的容器而言，如何确定外压计算长度，要视情况而定，如图1所示。对于容器的中部， 若存在加强圈和能有足够抗弯惯性矩的构件，则可以认为该处作为支撑线，若圆筒与椭圆封头、球形封头等凸形封头相连，则外压计算长度应包括封头曲面深度的1/3（EN 13445-3标准 取 封 头 曲 面 深 度 的0.4）。 AMSE Ⅷ-1 和EN 13445-3中有关筒-锥结构外压计算长度的具体规则如下所述。

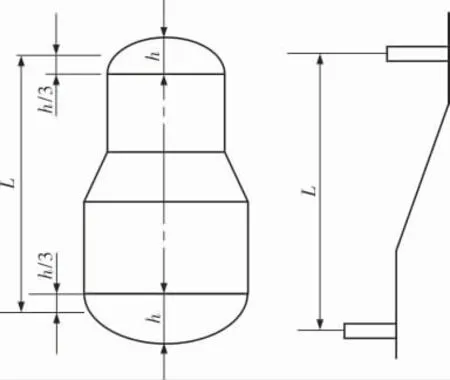
图1 GB 150—2011和ASME Ⅷ-1的外压计算长度

1.1 GB 150—2011和ASME Ⅷ-1

GB 150—2011和ASME Ⅷ-1常规设计中，关于筒-锥结构的外压计算长度视其连接处能否成为支撑线而定。 如果大小端的惯性矩满足最小所需的加强圈惯性矩，则可以作为支撑线，否则应按图1取其计算长度。 具有能满足设计要求的夹套与内筒连接的封闭线也可作为支撑线。 关于筒-锥结构的外压计算长度，GB 150—2011 和ASME Ⅷ-1均取Lcyl+LX， 即圆筒的轴向长度Lcyl加上锥壳的轴向长度LX。 ASME Ⅷ-2的外压计算长度与ASME Ⅷ-1没有区别。

1.2 EN 13445-3

EN 13445-3外压计算长度规则如图2所示，外压筒-锥结构设计时， 当锥壳的半锥角α＜30°时，外压计算长度L=Lcyl+Lcon；当α≥30°时，将锥壳大端与筒体连接处作为支撑线考虑，此时外压计算长度L=Lcyl。相比较EN 13445-3标准外压计算长度的规则， 由于ASME Ⅷ-1的外压计算长度的取值更大，因此相对比较保守。

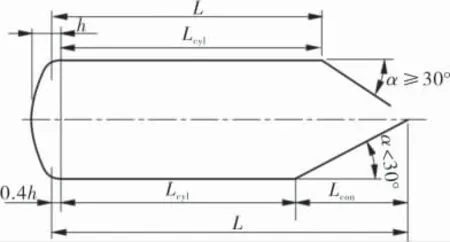
图2 EN 13445-3外压计算长度

1.3 筒-锥结构当量方法的设想

设想能否将锥壳段的当量长度来作为筒-锥结构的附加计算长度。 基于这种设想并结合EN 13445-3标准的外压计算长度的规则，将α≥30°时筒-锥不连续处作支撑线处理，α＜30°时筒-锥结构当量成圆筒。 具体表述如下：α＜30°，筒-锥结构连接处不作支撑线考虑时，筒-锥结构当量长度Lecyl=Lcyl+Le， 即圆筒的轴向长度加上锥壳的当量长度。 对于无折边锥壳，其当量长度Le=（LX/2）（1+D1/D2）；对于大端有折边锥壳，其当量长度为锥壳的当量长度加上折边过渡段的轴向长度， 即Le=rsin α+（LX/2）（1+D1/Dc）。筒-锥结构的当量方法如图3所示，由图中几何关系可知，无折边即为折边半径r=0的特殊情况。

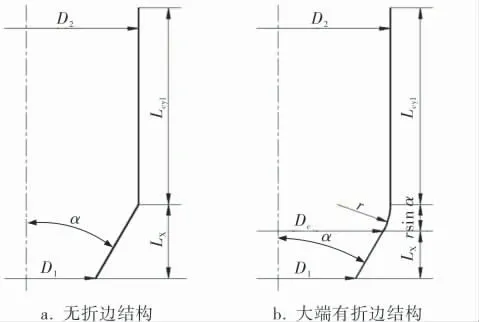
图3 筒-锥结构的当量方法示意图

1.4 当量长度与轴向长度的对比

GB 150—2011和ASME Ⅷ-1的外压计算长度都是筒-锥结构的轴向长度，将筒-锥结构的轴向长度与笔者所提出的当量计算长度进行对比。 以锥壳大端直径（圆筒直径）D2=2000 mm，半锥角α=20°为例，单一锥壳的当量长度Le与轴向长度LX的对比如图4所示。

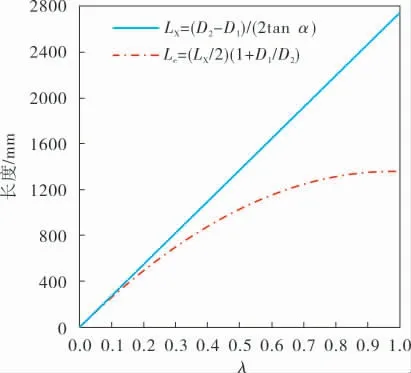
图4 锥壳当量长度与轴向长度的对比

由图4可知，锥形比λ（λ=1-D1/D2）较小时（锥壳较短），当量长度比轴向长度略小；锥形比λ=1，此时当量长度为轴向长度的一半。 α＜30°时，对于大端有折边锥壳，其当量长度为锥壳段的当量长度加上折边段的轴向长度。 折边半径越大，折边段越长，锥壳段越短，当量长度与轴向长度越接近。 结合图3、4可知，α＜30°时，无论是无折边结构还是带折边结构， 筒-锥结构的当量长度都要比轴向长度短，外压计算长度取轴向长度时比文中的当量长度保守。

1.5 ASME Ⅷ-1和GB 150—2011的折边设置要求

折边的存在可以缓解不连续区的应力集中［5］，GB 150—2011和ASME Ⅷ-1对于锥壳大端常规设计规定都是：α≤30°时， 允许无折边；α≤60°时，应有折边；α＞60°时，按平盖设计（或应力分析）。所不同的是：GB 150—2011 规定折边半径r≥0.1D2且r≥3t；ASME Ⅷ-1规定折边半径r≥0.06D2且r≥3t；ASME Ⅷ-2分析设计［6］对于筒-锥连接处无论是否有加强圈都可采用无折边结构，但不连续处的应力需满足应力强度限制。 针对以上规则，文中的所有算例均有r≥0.1D2=200 mm。

2 有限元模拟方案

2.1 有限元验证技术路线

对于α＜30°的筒-锥结构， 如果当量圆筒的屈曲压力小于原筒-锥壳结构的屈曲压力，则此方法是保守可行的； 如果当量圆筒的屈曲压力大于原筒-锥壳结构的屈曲压力，则此方法是不保守的。

2.2 有限元建模尺寸

2.2.1 初始筒-锥结构模型

锥壳的半锥角α取10、20°； 锥壳大端直径与厚度比D2/t=200；锥壳小端直径与厚度比D1/t在0～180间取值，间隔为20。 筒-锥结构筒体段长度与圆筒直径比Lcyl/D2取值0.5、1.0、2.0、4.0。 对于有折边的筒-锥结构，其折边半径与圆筒直径比r/D2在0.1～0.4间取值，间隔为0.1。文中的模拟计算模型，取圆筒直径D2=2000 mm，t=10 mm。

2.2.2 当量圆筒模型

将上述的初始筒-锥结构当量成一个圆筒，其当量圆筒的直径d=D2， 当量厚度仍为筒-锥结构厚度t。 对于α＜30°的筒-锥结构，其当量长度为初始筒-锥结构圆筒的轴向长度加上锥壳的当量长度。

采用ANSYS有限元建模计算，进行特征值屈曲计算验证。 选择Shell181单元建模，初始筒-锥结构的网格精度与其当量圆筒的相同，边界条件简支，两端节点施加等效轴向力。

3 α＜30°筒-锥结构模拟结果及讨论

3.1 屈曲模态

半锥角α=10°、α=20°；筒体长度Lcyl取值为1 000、2 000、4 000、8 000 mm；锥壳的小端直径D1从1 800 mm到0 mm； 部分模型的初始筒-锥结构及其当量圆筒的屈曲失稳模态图如图5～7所示。

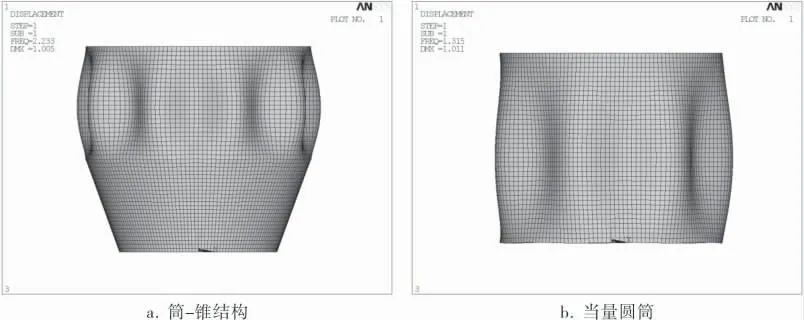
图5 α=20°、Lcyl=1000 mm、D1=1400 mm模拟结果

3.2 计算结果

半锥角α=10°、α=20°； 计算过程将筒体长度设为固定值Lcyl=1000 mm，锥壳的小端直径D1从1 800 mm到0 mm；再将锥壳小端设为固定值D1=1800 mm，筒体长度Lcyl计算范围为1 000～8 000 mm，计算结果列于表1～4。

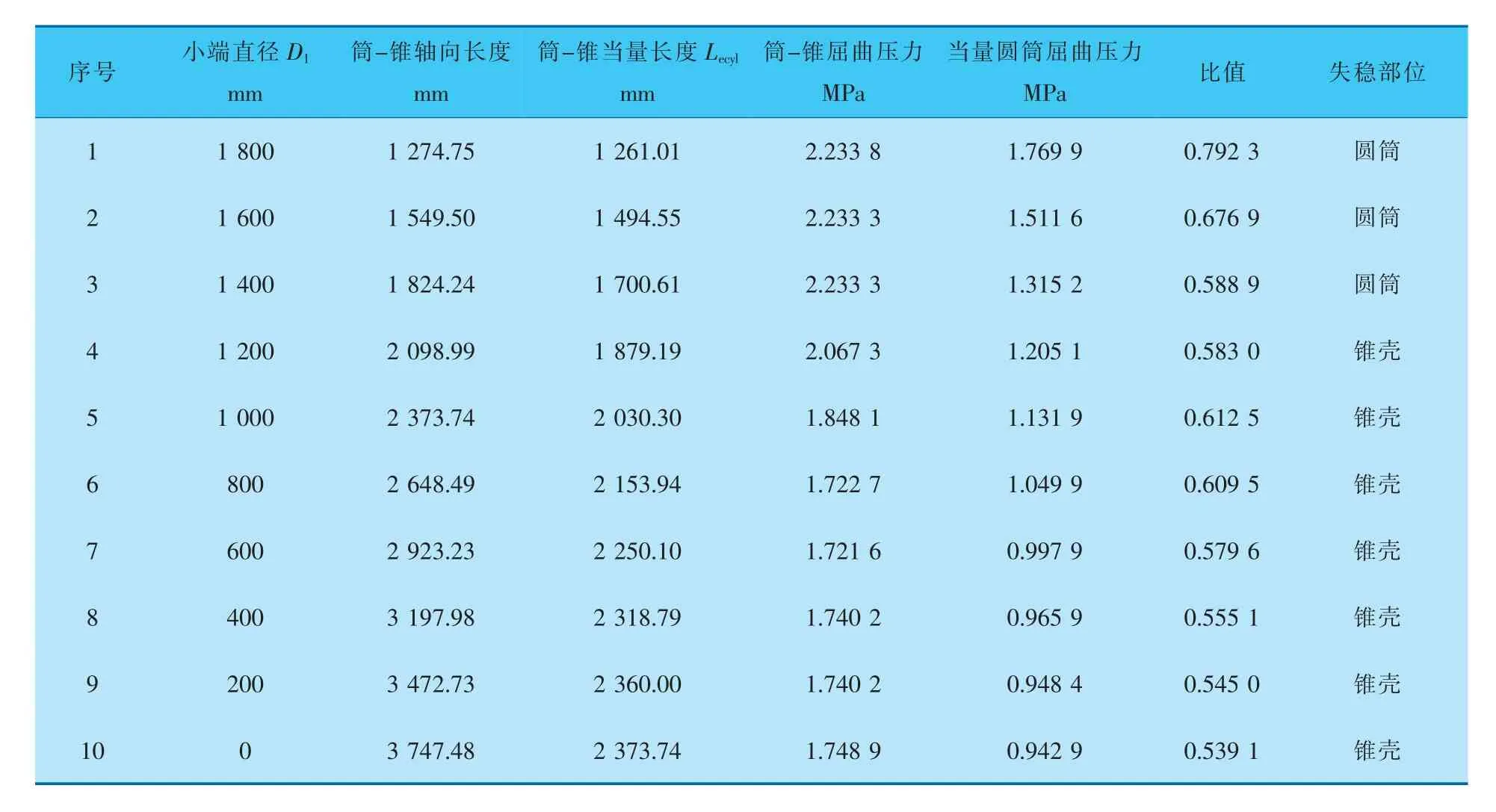
表1 α=20°、Lcyl=1000 mm、D1变化时的计算结果

图6 α=20°、Lcyl=1000 mm、D1=1200 mm模拟结果

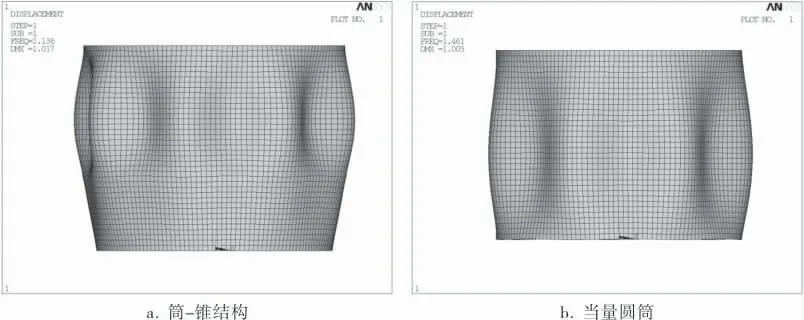
图7 α=10°、Lcyl=1000 mm、D1=1400 mm模拟结果

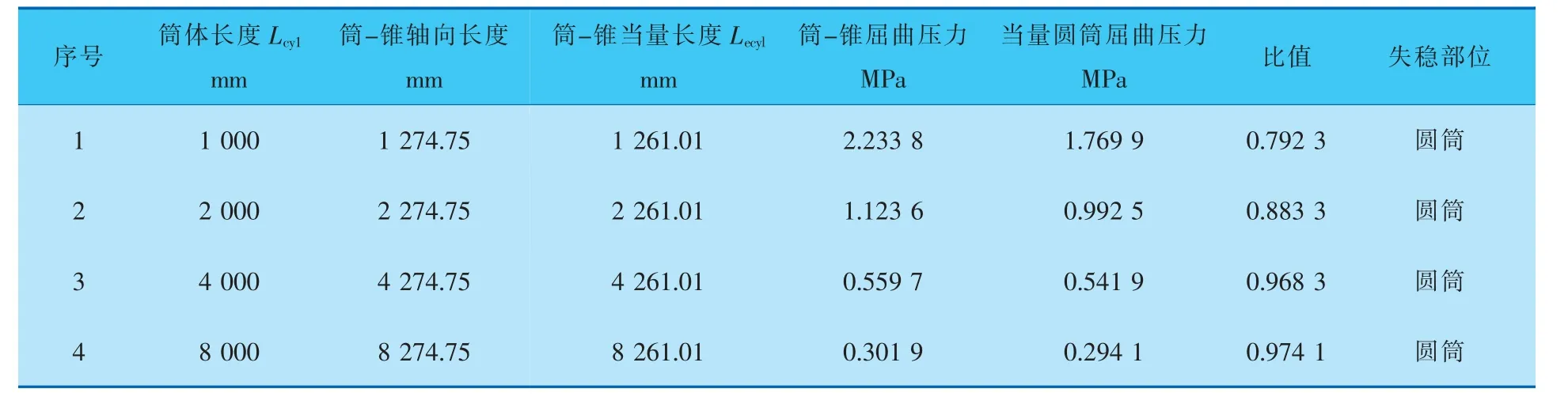
表2 α=20°、D1=1800 mm、Lcyl变化时的计算结果

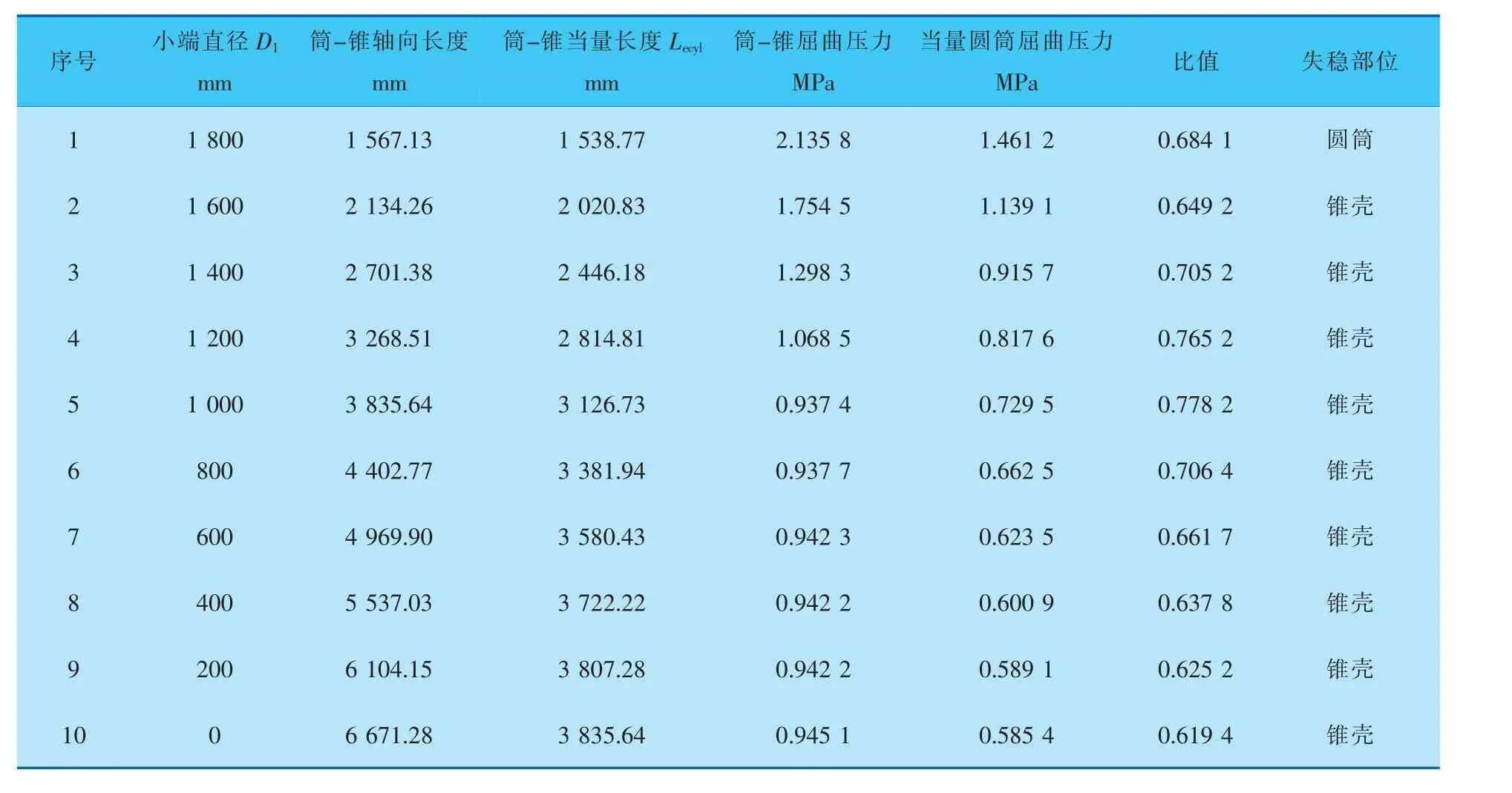
表3 α=10°、Lcyl=1000 mm、D1变化时的计算结果

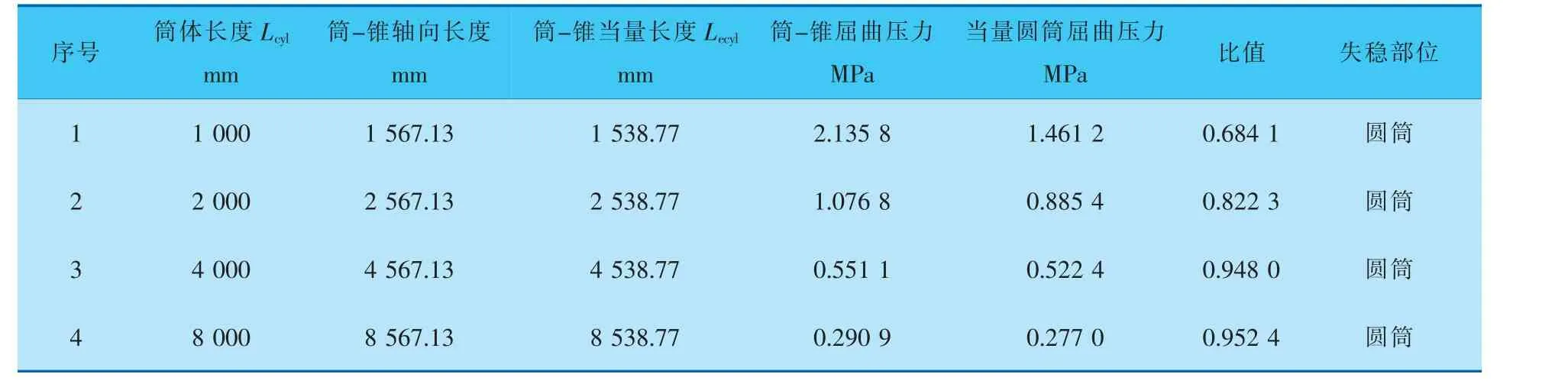
表4 α=10°、D1=1800 mm、Lcyl变化时的计算结果

3.3 讨论

半锥角α取20、10°时， 有限元特征值模拟计算结果都表明当量圆筒的屈曲压力小于初始筒-锥结构的屈曲压力。 α＜30°时， 文中所提无折边筒-锥结构的外压计算长度当量方法是保守可行的。 当量圆筒屈曲压力与初始筒-锥结构屈曲压力的比值为0.5～1.0。 当屈曲发生在锥壳段时，其比值接近0.5（即当量方法越保守）；当失稳发生在筒体段时，筒体长度越长，锥壳越短，比值越接近1.0（即当量方法越等效）。

4 α＜30°带折边模拟结果及讨论

4.1 屈曲模态

部分模型（α=20°、Lcyl=1000 mm、D1=1800 mm）的初始筒-锥结构及其当量圆筒的屈曲失稳模态图如图8所示。 从图8所示的模拟结果可以看出，折边过渡段也发生了屈曲。

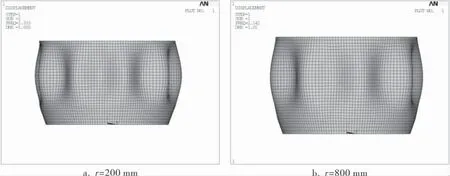
图8 α=20°、Lcyl=1000 mm、D1=1800 mm模拟结果

4.2 计算结果

半锥角α=20°进行有限元模拟验证， 由3.3节的讨论可知当圆筒和锥壳的长度相差越大时，其比值越接近1.0。 在进行不同折边半径r计算时，锥壳小端设为固定值D1=1800 mm（锥壳段最短），筒体轴向长度的计算范围是1 000～8 000 mm。 α=20°、D1=1800 mm，r的范围为200～800 mm。计算结果见表5～8，失稳部位均是圆筒。

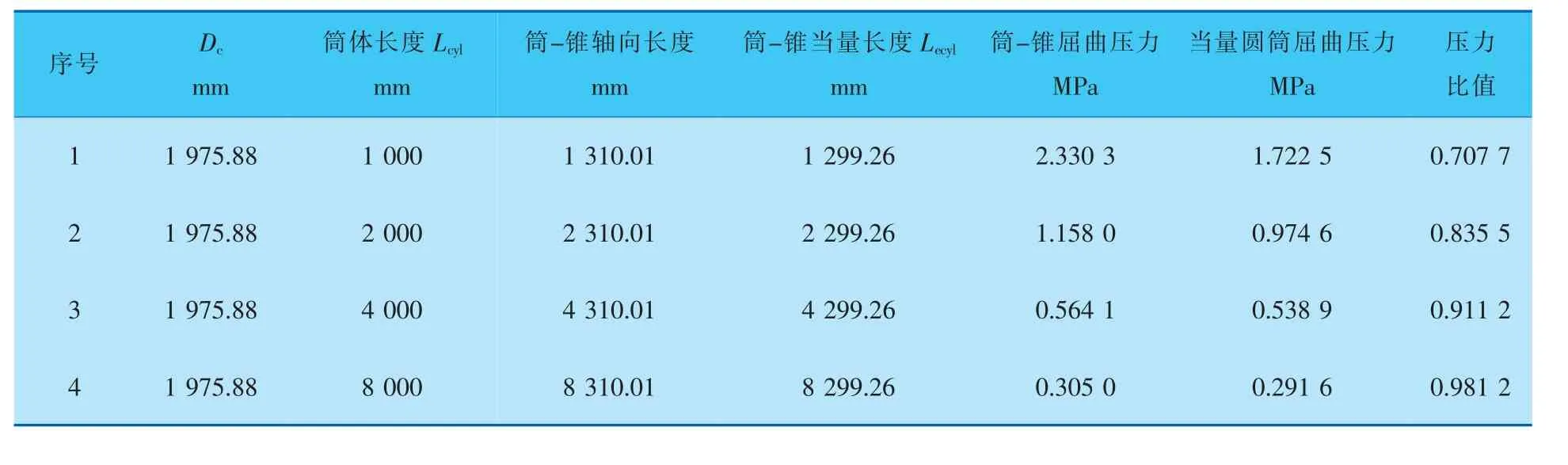
表5 α=20°、D1=1800 mm、r=200 mm计算结果

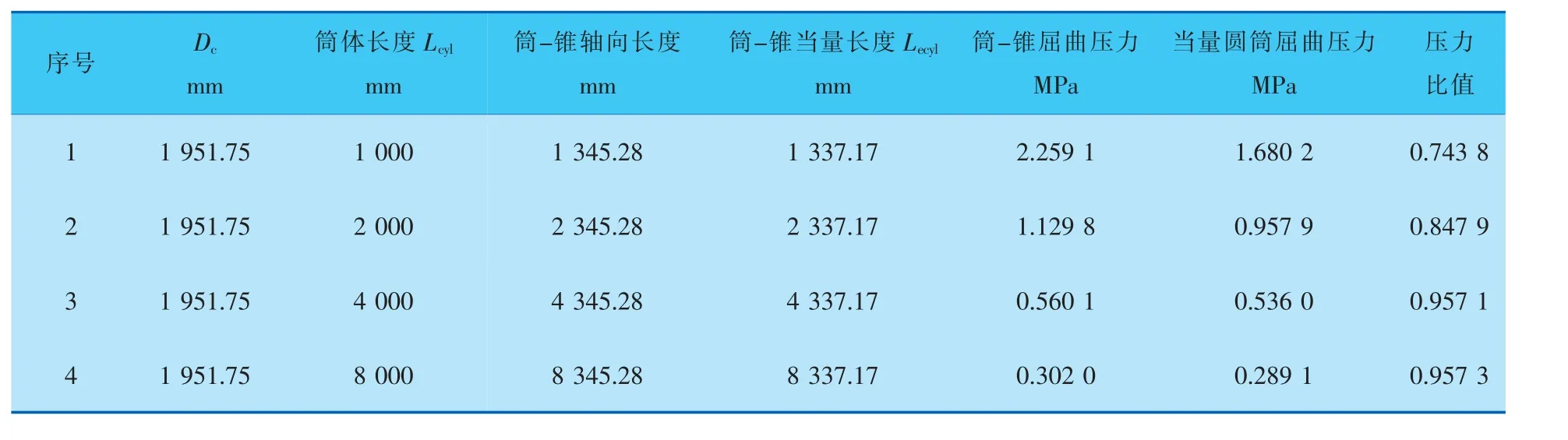
表6 α=20°、D1=1800 mm、r=400 mm计算结果

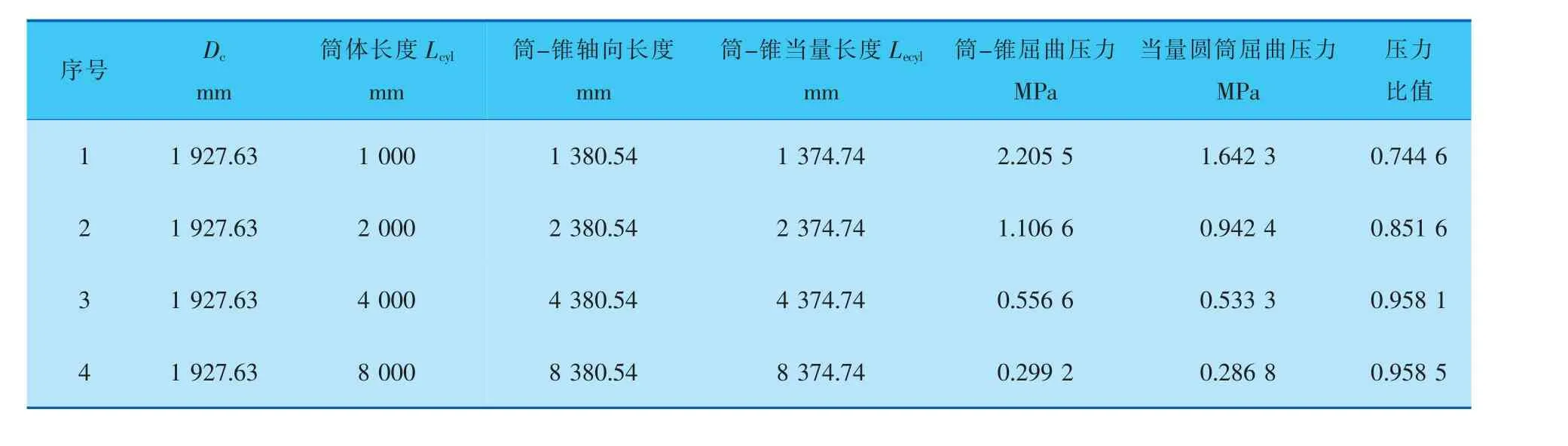
表7 α=20°、D1=1800 mm、r=600 mm计算结果

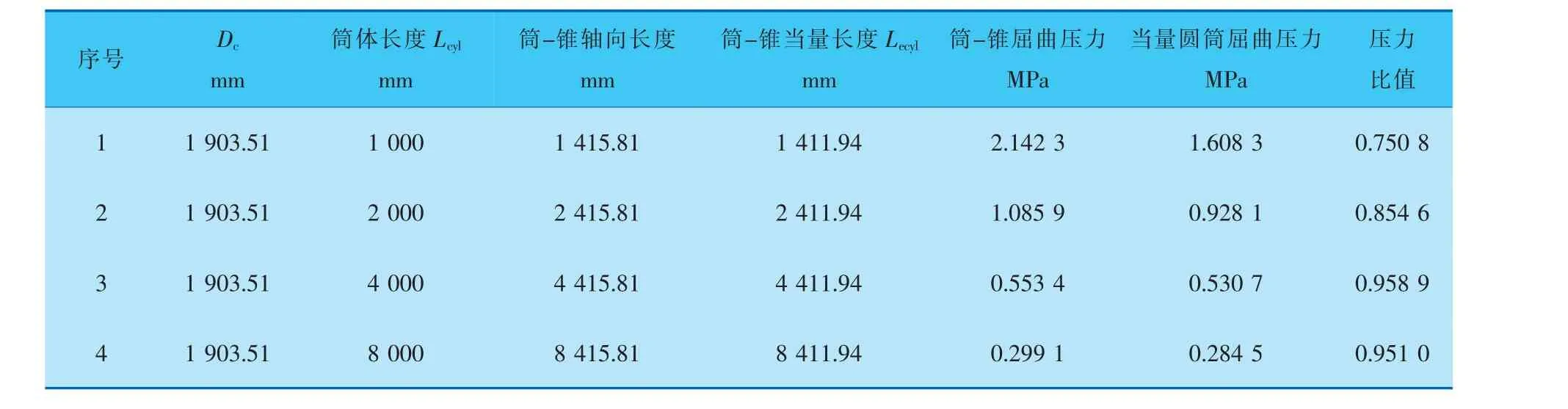
表8 α=20°、D1=1800 mm、r=800 mm计算结果

4.3 讨论

为方便分析讨论， 以折边半径r为横坐标，以当量前后的压力比值为纵坐标，Lcyl值为参变量，将模拟计算结果绘制如图9所示。

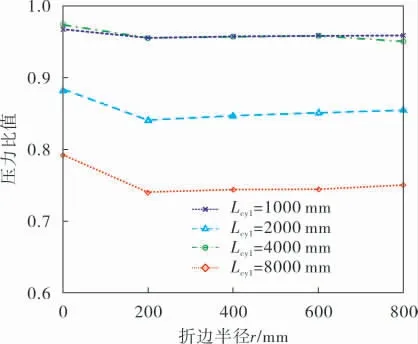
图9 不同折边半径下的屈曲压力比值

半锥角α为20、10°时，带折边筒-锥结构有限元特征值模拟计算结果都表明当量圆筒的屈曲压力小于初始筒-锥结构的屈曲压力。 α＜30°时，文中所提带折边筒-锥结构的外压计算长度当量方法是保守可行的， 当量圆筒屈曲压力与初始筒-锥结构屈曲压力的比值范围是0.7～1.0。 如图9所示，带折边结构比无折边的压力比值小，即当量方法越保守。 筒体Lcyl越大（即与锥壳段的当量长度Le相差越大），比值越接近1。

5 结论

5.1 当半锥角α≥30°时，EN 13445-3把锥壳大端与筒体连接处作支撑线考虑， 而GB 150—2011、ASME Ⅷ-1 不作支撑线考虑。 GB 150—2011、ASME Ⅷ-1外压计算长度的取值比EN 13445-3保守。

5.2 当半锥角α＜30°时，有限元特征值计算表明：筒-锥结构外压计算长度取Lecyl=Lcyl+Le是保守可行的。

5.3 文中所提的筒-锥结构当量方法是合理可行的， 且比传统的取轴向长度的方法更合理，改进了工程设计中筒-锥结构的外压计算长度。