计量中回归模型参数值及其不确定度评估

白 杰，胡红波

(中国计量科学研究院，北京 100029)

1 引 言

自GUM实施以来，国内外学者做了很多研究与讨论[1～4]，包括从统计学不同角度(经典统计与贝叶斯统计)分析其特点与不足之处，这对后期GUM的修订以及相关补充标准文件的发布实施起到了很大的作用[5～8]。

在实际的计量校准工作中，除了直接对被测量进行分析以外，回归分析也是一种常用的数据分析方法。比如在振动加速度计量校准中，要通过回归分析从测量得到的数据中计算出表征运动数学模型的参数，即幅度和相位等信息。有些仪器，其输入输出关系本身就是一个线性回归模型，比如风速传感器输出电压与风速的关系。对于简单的线性回归模型Y=θ0+θ1X，其参数至少包含回归直线的截距θ0与斜率θ1参数，因其无法转换一个确定的单一被测量模型[9]，无法直接依据GUM系列文件的规定进行处理。本文依据GUM不确定度评估的准则，针对计量中回归模型参数计算的问题，在测量数据的基础上采用最小二乘与贝叶斯推断参数计算的方法计算了参数值以及相应的不确定度。对于多参数计算的问题，通常需采用马尔科夫链蒙特卡洛(Markov chain Monte Carlo，MCMC)法进行数值计算[10]。本文也采用了MCMC方法，并且与最小二乘方法进行了比较，说明2种方法的相同与不同之处。

2 测量模型与统计模型

2.1 GUM与测量模型

依据GUM系列文件进行不确定度评估，首先需建立测量模型。测量模型表示被测量θ与各输入量(Y,X)之间的函数关系，为了便于说明，假定测量模型如式(1)所示线性关系，实际测量模型可依据测量过程建立。

θ=φ(Y,X)=αY+βX

(1)

式中：θ为被测量；Y为通过测量得到的数据；X为通过其他方式得到的被测输入量；α、β为固定常系数。通过测量得到一组数据Y后，依据GUM即可确定被测量θ的最佳估计值与不确定度。另外，若能依据测量过程以及其他信息确定测量方程(1)中所有输入量的联合分布fxy(x,y)，且能对其进行抽样，则能够采用GUM S1中的方法确定被测量的近似概率密度函数，最终得到被测量的最佳估计值以及任意置信概率下区间。

2.2 贝叶斯推断与统计模型

贝叶斯推断主要是指利用贝叶斯定理计算参数的方法与过程，其出发点是数据，目的是为了得到参数的后验分布。贝叶斯定理形式如式(2)所示。

π(θ|y)∝L(y|θ)π(θ)

(2)

式中：π(θ|y)为参数的后验分布；L(y|θ)为似然函数，即测量数据的分布；π(θ)为参数的先验分布，即在测量数据得到之前对参数的认识。

为了利用贝叶斯定理，首先需建立数据的统计模型，也称为数据观测方程[7]。对于式(1)所示的测量方程，相应的观测方程如式(3)所示。

(3)

式中ε为测量过程中的噪声。若相互独立的测量过程得到的数据y=(y1,y2,…,yN)，且噪声ε为均值为0、方差为σ2的正态分布，即ε～N(0,σ2)。则式(2)所示的似然函数为如式(4)所示。

(4)

参数先验分布的确定也是利用贝叶斯定理的一个关键条件。在计量校准的实际工作中，对某一个确定校准对象，往往都会有较为明确的经验信息，比如前面做过同样型号的校准，或者往年对同一对象校准的数据等。如何由先验信息转化为先验分布以及先验分布的各种取法可参考文献[11]。对式(3)所示的测量方程而言，输入量x与被测量θ可根据依据GUM S1推荐的确定输入量分布的方法根据先验信息确定其合适的分布分别为π(x)与π(θ)。对被测量若无先验信息，则可取π(θ)∝C，C为常数。对测量过程中的噪声方差，通常取其无信息先验形式，即π(σ2)∝(σ2)-1。由此可得被测量θ的后验分布如式(5)所示。

π(θ|y)∝∬L(y|θ,σ2,x)π(σ2)π(x)π(θ) dxdσ2

(5)

由此也可以看出，应用贝叶斯推断进行参数不确定度分析，不需要再进行A类与B类方法的区分。

另外，若式(3)所示的观测方程α、β未知，同样可应用贝叶斯推断对其进行估计。假定参数α、β的先验分布π(α,β)，则所有参数的联合后验分布如式(6)所示。

π(α,β)π(x)π(θ)π(σ2) dx

(6)

对式(6)所示的联合分布进行积分，则可得到关于任何参数的后验分布。比如参数α、β的联合后验分布为式(7)所示。

π(α,β|y)=∬π(θ,α,β,σ2|y) dθdσ2

(7)

3 回归模型参数的确定

对于式(1)或式(3)所示的模型，均可以通过变换将其等效为统一的关于参数的线性测量模型。假定某一计量校准过程，在给定的一组设定试验条件X=(X1,X2,…,Xp)下，被校对象的输出Y如式(8)所示。

Y=β0+β1X1+…+βpXp+ε

(8)

为简化表示，将式(8)写成矩阵形式，即Y=Xβ+ε。Y=(y1,y2,…,yN)T为N组不同设定试验条件下被校仪器的输出；X=(1,xi1,xi2,…,xip)(i=1,2,…,N)为一个N×(p+1)维的矩阵；β=(β0,β1,…,βp)T为待确定的参数；ε为N维噪声向量。

3.1 最小二乘算法

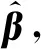
S(β)=argmin(Y-Xβ)T(Y-Xβ)

(9)

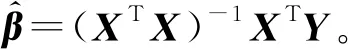
=σ2(XTX)-1

(10)

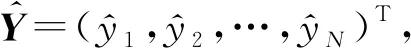
(11)

在得到参数估计值协方差矩阵后，其对角线上元素即为估计参数的方差，即

(12)

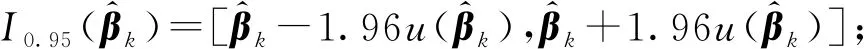
3.2 贝叶斯推断参数估计

对于式(8)所示的回归模型，为了便于分析参数计算过程，通常假定测量噪声ε～N(0,σ2I)。在得到N组不同设定试验条件下被校仪器的输出Y后，可得似然函数为：

L(Y|β,σ2)=(2πσ2)-N/2·

(13)

对于参数β，假定其先验分布为π(β)且互不相关，即π(β)=π(β0)π(β1)…π(βp)，噪声方差的先验分布为π(σ2)，可得参数的后验分布为：

π(β,σ2|Y)∝L(Y|β,σ2)π(β)π(σ2)

(14)

有了所有参数的联合后验分布，则可以通过积分得到感兴趣参数的后验分布，从而计算参数的最佳估计值以及相应置信概率下的区间。从式(14)可以看出，当校准对象的回归模型参数较多(大于3个)时，通常难以通过积分得到单个参数概率分布的解析解，需采用MCMC算法来对后验分布进行数值计算。

4 实 例

4.1 加速度计的振动校准

加速度计，特别是压电加速度计，在科学研究与工程实践中广泛应用于机械结构振动冲击测量以及状态监测。频率响应和幅值线性度是加速度计2个关键的指标。对于加速度计频率响应的校准，一般采用振动校准法。图1是在设定频率100 Hz，且振动加速度幅度大约50 m/s2下时，激光干涉仪测量得到的振动台运动的加速度波形数据。

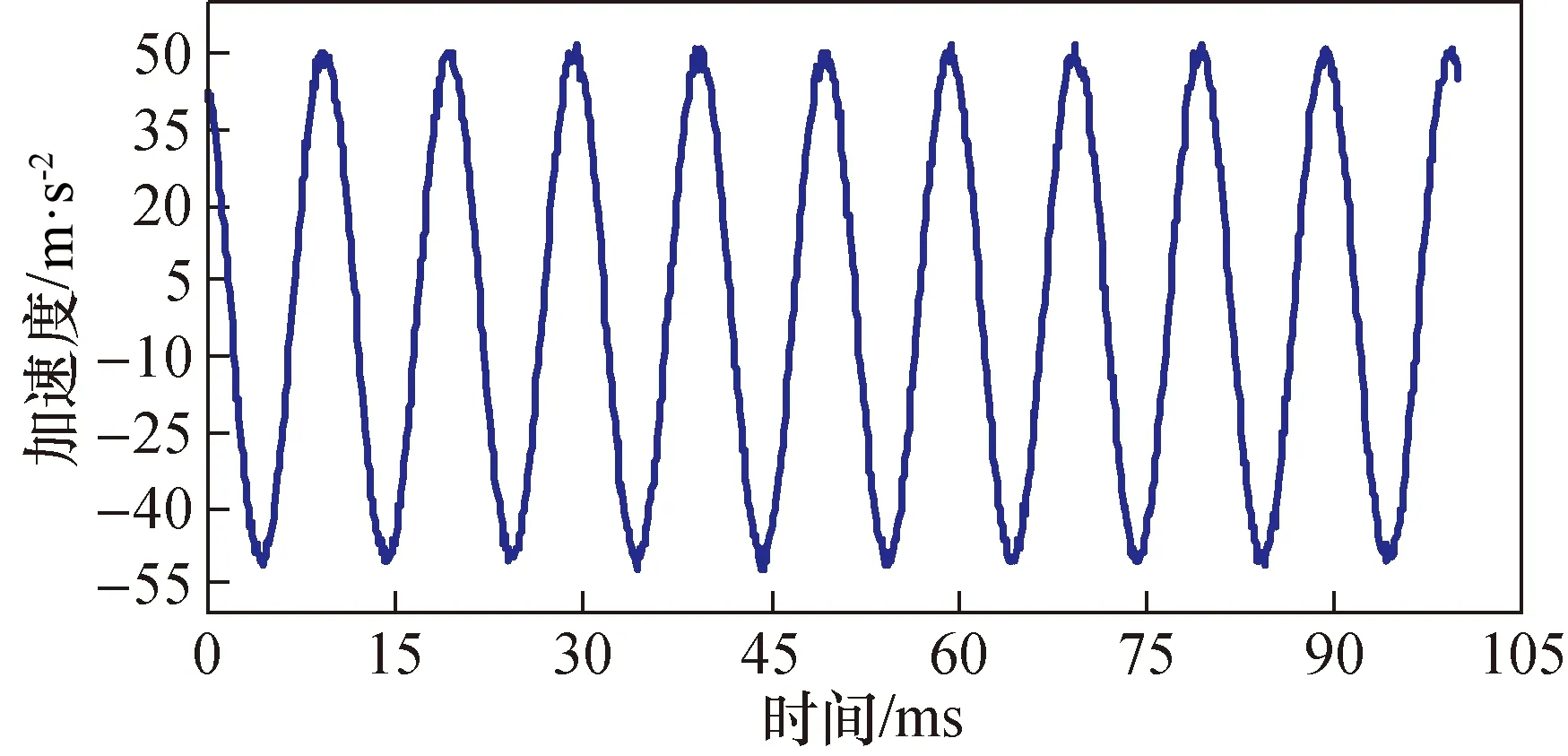
图1 振动台运动的加速度波形Fig.1 Acceleration waveform of vibrator

为了得到图1所示序列的幅度和相位等信息，我们采用回归的方法。由于振动台按正弦规律运动，故可设定其加速度波形为式(15)所示，即：

a(t)=A0cos(ω0t+θ0)+C0

(15)

式中：A0与θ0为关注且需确定的参量；ω0为设定的振动台工作频率；C0为未知的直流分量。对其按式(8)形式进行展开并对参数做适当变换可得[13]：

a(t)=A0cos(ω0t)cos(θ0)-A0sin(ω0t)sin(θ0)+C0

=A1cos(ω0t)-A2sin(ω0t)+C0

(16)

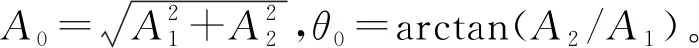
(17)

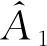
为了利用贝叶斯定理对参数进行推断，需设定参数的先验分布π(β,σ2)，假定各参数之间是相互独立的，即π(β,σ2)=π(β)π(σ2)=π(A1)π(A2)π(C0)π(σ2)。直观观测图1所示加速度波形图再结合参数A1与A2的形式，设定π(A1)π(A2)～Unif[-60,60]，即为从-60到60之间的均匀分布，同时π(C0)～Unif[-10,10]，考虑到方差为尺度参数且必须大于0，选择π(σ2)～χ2(3)，该范围包括了实际振动加速度校准过程中所有方差可能取到的值。利用MCMC数值计算的方法，对式(16)模型参数进行贝叶斯推断，得到主要参数的后验分布样本、概率分布图以及95%的区间(阴影部分),如图2所示。

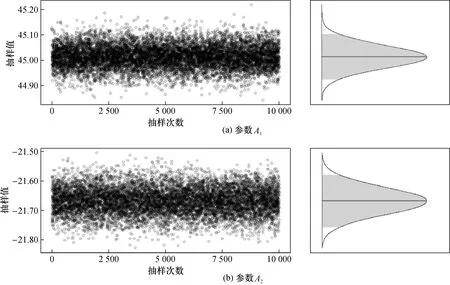
图2 参数A1与A2的后验分布抽样值与概率分布Fig.2 Samples and posterior distribution of parameter A1 and A2

从2种方法计算的结果可以看出，在参数先验分布取弱信息先验分布且数据量较多的情况下，2种方法计算的结果基本一致；同时从图3也可以看出，2个参数基本相互独立，这也与前面计算的结果一致。但当数据量较少时，先验分布的选取对参数计算的结果有较大的影响[14]。

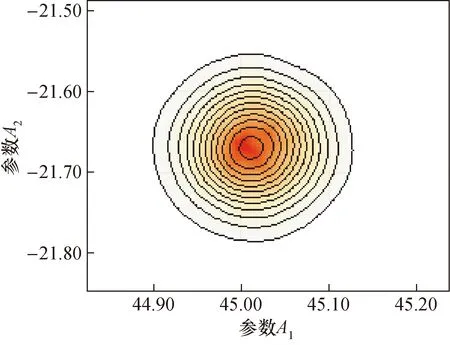
图3 参数联合分布Fig.3 Joint probability distribution for parameters

4.2 加速度计的冲击校准

加速度计的幅值线性度指标，通常采用冲击的方式校准。将被校加速度计安装在标准冲击校准台上，测量输入加速度计的冲击加速度量值a(单位m/s2)，同时记录加速度计的输出电压量y(单位mV)。设定加速度计输入输出是一个线性关系，即y=b+ka。由1组测量的数据即可确定直线截距b与系数k的值，再依据相关规程即可计算出被校加速度计在试验范围内的线性度指标。表1为1典型的加速度计在冲击加速度范围1.0×102～5.0×104m/s2的试验结果。

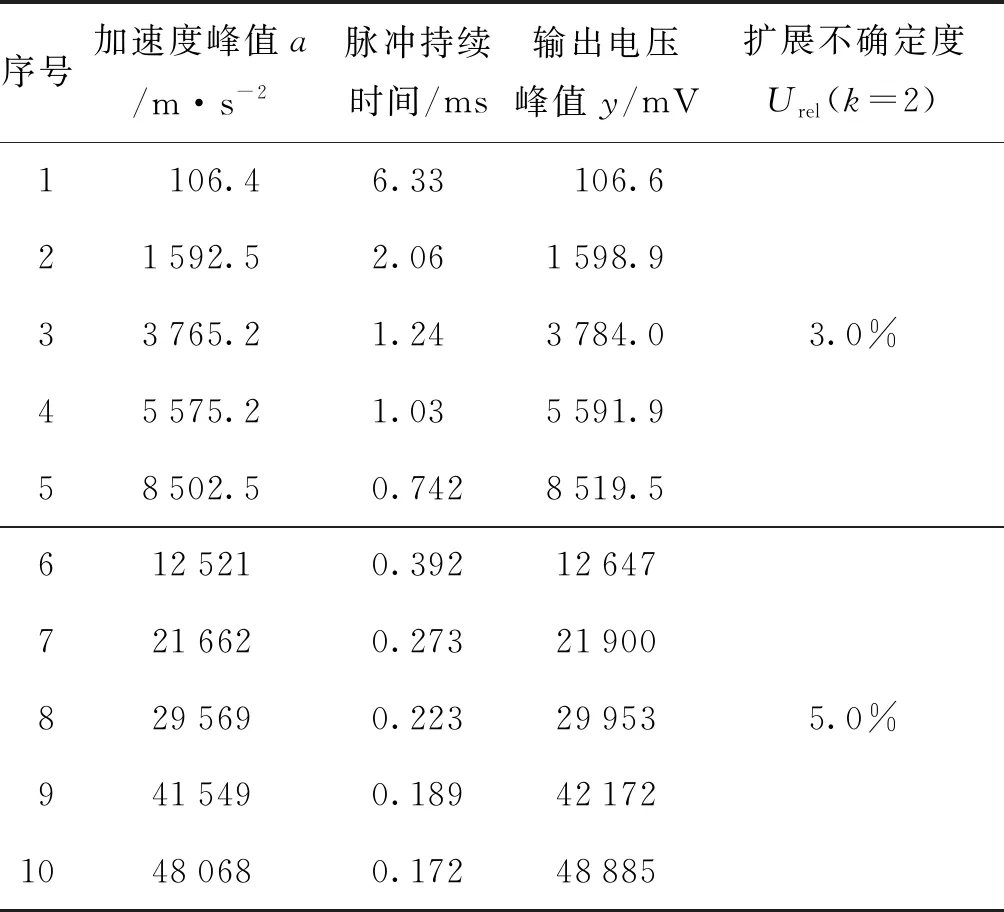
表1 加速度计冲击校准结果Tab.1 Calibration results of acceleromter by shock

表1中的脉冲持续时间为冲击校准的一个试验条件，此处不是我们关注的对象。与振动校准不同，冲击校准在不同的范围有不同的测量不确定度，也就是测量噪声模型为ε～N(0,σ2Ω)，Ω为N×N非奇异正定且对称矩阵。故应采用加权最小二乘算法进行参数的计算。此时式(9)变为如式(18)所示[7,15]。

S(β)=argmin(Y-Xβ)TW(Y-Xβ)

(18)

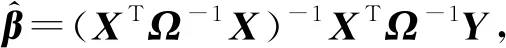
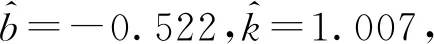
(19)

利用贝叶斯推断首先确定参数的先验分布。对于斜率，由同类加速度计校准经验数据可知该加速度计的灵敏度范围在0.5到1.5之间，可设定π(k)～N(1,0.252)；对于截距，通常没有1个明确的范围，故可设定为无信息先验分布，即π(b)∝C，C为常数。利用MCMC算法，计算得到2个参数的后验分布以及后验联合分布分别如图4所示。

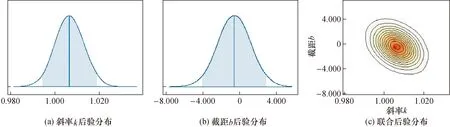
图4 斜率与截距的后验分布Fig.4 Posterior distribution for slope and intercept

5 小 结

通过测量数据计算参数的值，即将参数表示为数据的函数，本文所述的最小二乘法与贝叶斯推断法(包括参数的极大似然估计等)都是应用较为广泛的方法。其中贝叶斯推断的最大的优点在于可以利用计量校准中的经验信息或者是以前校准的数据，并且以1种符合逻辑的方式并入测量数据的分析。本文对上述2种方法通过实际校准中的例子进行了比较，最小二乘法计算非常简洁方便，可以迅速的得到参数的值；而贝叶斯推断则计算较为复杂，通常需要采用数值计算的方式，但其能充分利用计量校准中的经验和历史数据等信息。实际工作中可根据情况选择合适的方法。