基于机器学习算法的超声流量计使用中检验

李梦娜, 吕承泽, 王 蕾, 李春辉

(1.中国计量科学研究院,北京 100029; 2.中国计量大学,浙江 杭州 310018)

1 引 言

近年来,超声流量计由于准确度高、无移动部件、无压力损失等特点,越来越广泛地应用在油气、天然气等贸易交接计量中[1]。在大口径气体流量测量中,主要采用时差法多声道超声流量计[2,3]。天然气是一种低碳的化石类一次能源,随着我国能源结构的调整,天然气行业得到了快速发展。广泛应用于贸易交接计量的超声流量计的检定和校准需求与日俱增。天然气是易燃气体,运行中涉及到高压,因此,流量计的拆卸及安装需消耗大量人力并存在安全隐患;此外,受限于天然气计量站的检测能力,目前流量计检定和校准周期较长,严重影响生产运行。

依据JJG 1030—2007《超声流量计》检定规程,超声流量计使用中的检验用于在实流装置上检定完成后,在检定周期内对流量计计量性能可靠性的检查。开展使用中检验,可将超声流量计的检定周期由2年延长到6年[4]。采用使用中检验可显著降低生产运行成本,有效缓解送检的供需矛盾。机器学习算法作为一门人工智能科学,是对通过经验能够自动改进的计算机算法的研究[5]。目前已有一些机器学习算法在超声流量计检验领域的研究,然而模型的准确度等还难以满足实际应用的需求[6～9]。

本文采用随机森林机器学习算法,结合超声流量计使用中检验的具体问题,建立流量偏差预测分析模型,并对影响超声流量计准确度的特征变量进行分析,实现超声流量计的使用中检验。主要工作包括2个方面：1) 研究超声流量计使用中检验程序,通过获取流量计的信号质量、流态指标、计量性能等变量,对流量计各项性能开展诊断。2) 采用随机森林算法模型对超声流量计的流量测量偏差进行预测;并对模型结果进行不确定度评估,分析影响超声流量计使用中测量准确度的变量,实现对超声流量计使用中检验方法的完整评估。

2 研究基础

2.1 超声流量计

时差法超声流量计利用通过相同行程内超声波在顺流和逆流中的时间差,计算得到流动气体的平均流速[10]。流量计以测量声波在流动介质中传播的时间与流量的关系为原理。通常认为声波在流体中的实际传播速度是由介质静止状态下声波的传播速度和流体轴向平均流速在声波传播方向上的分量组成,顺流传播时间td和逆流传播时间tu与各量间的关系为：

(1)

式中:cf为声波在流体中的传播速度;vm为流体的轴向平均流速;φ为声道角;L为声道长度。

利用式(1)可计算得到流体流速和声波的传播速度：

(2)

(3)

(4)

依据JJG 1030—2007《超声流量计》,超声流量计使用中检验的方法主要有2种,分别是标准表串联法和声速检验法[4]。但现场设备、安装管路等因素往往限制了标准表串联法的使用,因此多采用声速检验法。

GB/T 30500—2014《气体超声流量计使用中检验-声速检验法》对声速检验法的评判方法和指标进行具体规定[11]:基于超声流量计不同声道的声速测量结果计算得到工况条件下的测量声速;基于热力学关系计算得到工况条件下的理论声速。将测量声速与理论声速间的差异作为超声流量计的核查参数,可确定超声流量计的状态。

由于没有具体可实施的使用中检验方法,超声流量计普遍的检定周期为2年。为形成1种可实施的超声流量计使用中检验方法,需要对影响超声流量计使用中准确度的全部变量进行监测和分析,明确各个变量对于超声流量计流量偏差的指示意义,从中提取特征变量,建立流量偏差预测模型,确保超声流量计使用中的准确度。

本文选择天然气站场实际运行的不同品牌型号的1台DN100、1台DN150及2台DN200超声流量计,建立基于机器学习算法超声流量计使用中检验方法。

2.2 随机森林算法

随机森林(random forest,RF)算法[12,13]以决策树为基学习器构建自主抽样集成,并在决策树训练过程中引入随机属性选择。在模型训练阶段,随机森林使用自助采样法,从输入的训练数据集中采集多个不同的子训练数据集来依次训练多个不同决策树[12]。每轮随机采样中,训练集中大约有36.8%的数据没有参与训练集模型的拟合,而用于计算袋外误差(out of bag error,OOB error)。在预测阶段,随机森林将内部多个决策树的预测结果取平均得到最终的结果,实现回归。

为保障实流检定后超声流量计使用中的计量性能,实流检定后可建立一种多变量的高维度数据预测模型,实现对使用中流量计测量偏差的高准确度预测。随机森林机器学习算法在解决此类问题中具有一定的优势。

首先,保证超声流量计流量偏差预测的准确度。随机森林采用集成算法,其本身预测准确度比大多数算法高。在训练过程中样本和特征随机性的引入,使其具备较强的抗过拟合能力,且OOB error的存在可以在模型生成过程中取得真实误差的无偏估计[14,15]。

其次,可以对影响超声流量计准确度的高维变量做出快速响应。随机森林简单易实现,计算量小,训练速度快,对数据集的适应能力强,使得其在处理多特征的高维数据方面极具优势。

此外,能够为分析影响超声流量计使用中准确度的各个变量的意义提供依据及验证。随机森林在训练过程中,能够检测到特征变量间的相互影响,并由此得到特征的重要性排序,在现实任务中表现出强大的性能[16]。

3 使用中检验方法—RF算法

3.1 特征变量提取

首先采集基本信息：超声流量计的品牌、口径、等级、最大流量点及最小流量点、超声探头的布置情况、仪表系数、检定信息、现场环境条件、安装条件、以及配套仪表(温度计、压力计、组分分析仪)的基本信息。

采集超声流量计使用中的工作数据。采集得到的实验数据经过计算分析处理,提取得到3类特征变量集,作为超声流量计流量使用中检验模型的输入变量,如表1所示。

表1 流量偏差预测模型的输入变量列表Tab.1 List of input features for flow deviation prediction

1) 信号质量。依据JJG 1030—2007,使用中检验应进行超声流量计的信号质量检查,指标包括：信号增益、信噪比等[4]。

2) 流态指标。JJG 1030—2007规定每声道的流速值与通流通量计的平均轴向流速值之比应在合理范围之内[4]。基于超声流量计的各声道流速、测量平均流速等,采用的流态判别指标通常包括剖面系数、对称性指标等。

3) 计量性能。主要包括声速检验数据、测量流量数据。根据GB/T 30500—2014中的指标的规定对声速检验数据进行评判[11]。声速检验数据,包括各声道声速、测量平均声速;此外,基于超声流量计处的工况温度、压力、组分数据,计算得到理论声速。利用理论声速和测量平均声速计算得到声速偏差。流量测量数据主要包括：超声流量计的测量流量,以及根据测量流速和横截面积计算得到的体积流量。

3.2 流量偏差预测模型的建立

对1台DN100、1台DN150及2台DN200超声流量计,根据采集到的实验数据,进行输入变量集的整理。此外,根据超声流量计最近一次实流检定结果,计算得到流量偏差作为的输出量,得到可用于拟合输入变量和流量偏差间关系模型的测试样本集。

然后对4台流量计的测试样本集,分别抽取得到训练样本。研究另外采集实验数据,按照输入变量和输出变量的要求,得到验证样本,从而保证验证样本的独立性。机器学习算法中训练样本和测试样本的比例设置一般在2∶1～4∶1的区间内,因此本文研究的4台流量计的训练样本和验证样本的数据数量如表2所示。

表2 训练样本和验证样本数量Tab.2 Training sample and test sample

利用训练样本对随机森林模型进行训练,建立基于随机森林算法的预测模型并得到特征变量的重要性得分。利用建立的随机森林模型,使用验证样本对使用中超声流量计的流量偏差值进行预测,并对结果进行评估和分析。

4 结果与分析

4.1 RF算法预测结果

根据训练样本的输入变量集,利用训练样本对随机森林模型进行训练,随机森林的决策树的总棵数设置为500,每个节点的特征数量设置为输入特征变量总量的1/3。建立随机森林模型,得到特征的重要性得分。然后利用建立的随机森林模型,使用验证样本的输入变量集,完成对超声流量计使用中的流量偏差值的预测。实验中4台流量计流量预测值与真实值的偏差如图1所示。

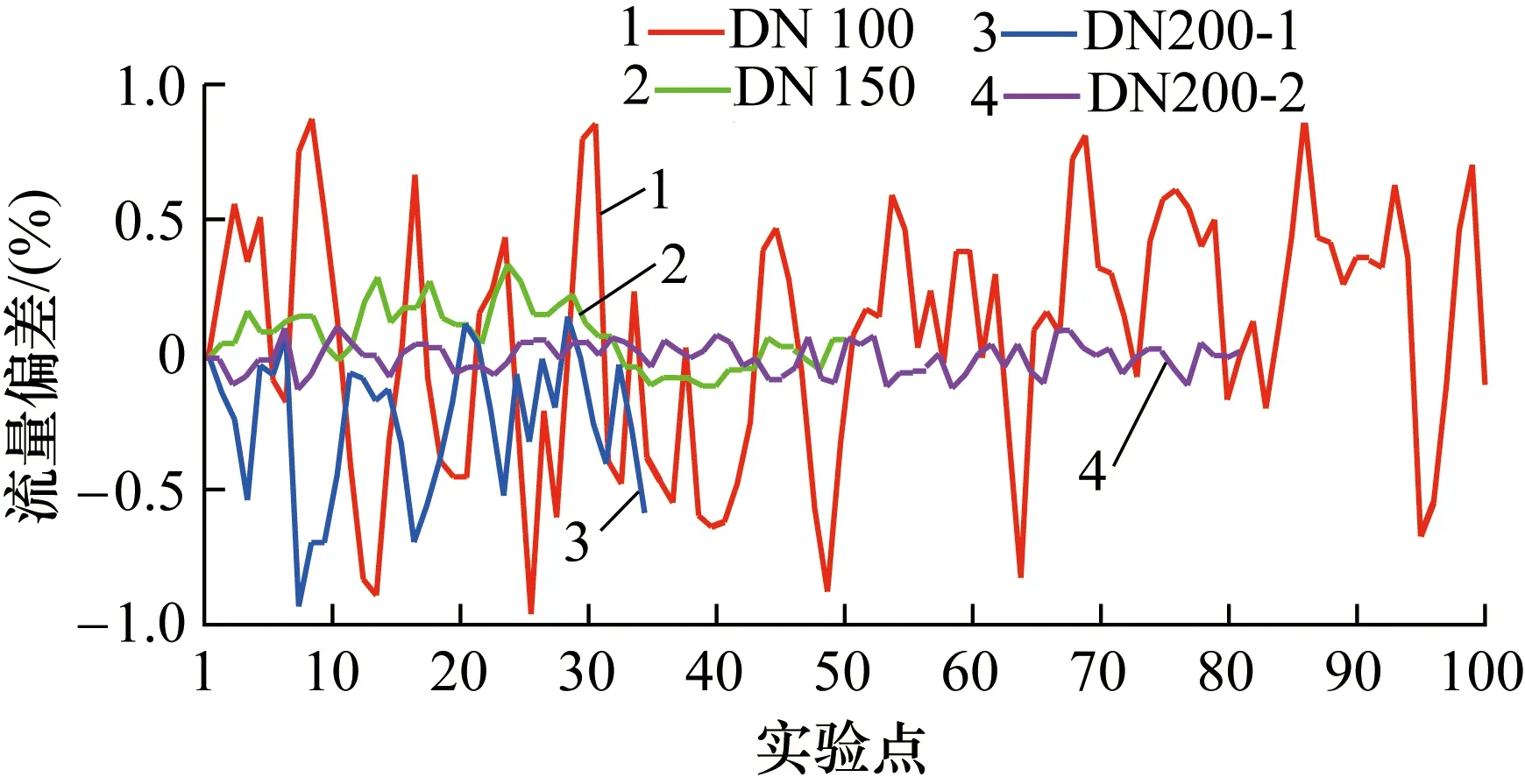
图1 预测结果与实际值的偏差Fig.1 The deviation of prediction results

由图1可知,对于超声流量计DN100的100个实验点,所有数据偏差的绝对值小于0.88%,其中83个数据点的偏差值在±0.5%以内。对于超声流量计DN150的50个实验点,所有数据的偏差值的绝对值小于0.26%。对于超声流量计DN200-1的35个实验点,所有数据的偏差的绝对值小于0.76%,其中31个数据点的偏差值在±0.5%以内。对于超声流量计DN200-2的80个实验点,所有数据的偏差的绝对值小于0.12%。

4.2 特征变量重要性分析

本文研究的RF算法,使用均方误差(mean square error,MSE)作为不纯度函数的指标,即针对决策树某1节点：

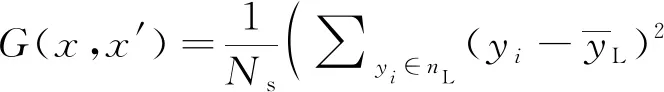
(5)

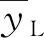
节点不纯度的增加代表了各变量对决策树各节点上观测值异质性的影响,该值越大表示变量的重要性越大[17]。节点的重要性Wi为

Wi=wi×Gi-wL×GL-wR×GR

(6)

式中：wi,wL,wR分别为节点i以及其左右子节点中训练样本个数与总训练样本数目的比例;Gi,GL,GR分别为节点i,以及其左节点、右节点的不纯度。确定每1个节点的重要性之后,即可以得到某一特征变量j的重要性得分：

(7)

式中：fj为特征变量j的重要性得分;∑i∈jWi为对于特征变量j的节点重要性之和;∑i∈JWi对于所有特征变量的节点重要性之和；J为特征变量节点数量。

对每一个特征变量重要性进行归一化处理,得到各个变量权重系数。超声流量计特征变量重要性得分及权重系数如表3所示(流量计型号：DN100)。

表3 特征重要性的得分及权重系数Tab.3 The importance score of the features and weight coefficients

图2 特征变量重要性排序Fig.2 The rank of the feature importance

依据权重系数进行排序,得到排名前10的变量,如图2(流量计型号：DN100)所示,排名前10的变量的权重系数均大于0.02。其中,计量性能数据中测量平均流速、计算流量、测量流量对于流量偏差预测的重要性最为显著。声速偏差、理论声速也表现出较高的重要性。此外,各声道的流速数据,也在重要性排名前10的特征变量中。

4.3 预测结果的评估

模型预测结果的评估分为2个方面:模型算法的不确定度评估以及各输入变量的不确定度评估。

4.3.1 模型算法的不确定度

依据方差整体解释率(variance explained)对随机森林算法的表现进行评估。方差解释率体现了预测变量对响应变量(所有的输入特征变量)间的关系,表示了模型的拟合优度,可以理解为模型的拟合的决定系数[18]。此外,预测值和观测数据残差是表征模型和真实过程之间差异的最好的定量指标,它们提供有价值的信息,可用于评估模型预的不确定性。通过模型的残差分布、以及输入变量和预测变量间的关系,进而分析预测模型输出值的不确定度[19,20]。因此,随机森林算法本身的不确定度ur,fit可以用模型拟合的残差来表示：

(8)

式中：Qdev,fit为超声流量计流量偏差预测值；Qdev为流量偏差的观测值。4台超声流量计的拟合优度和模型的不确定度如表4所示。

表4 随机森林模型拟合结果评估Tab.4 Evaluation of the performance of RF model

4.3.2 模型输入变量的不确定度

根据变量的重要性得分和权重系数排序,鉴于输入变量中流态指标的5个变量的权重系数较小,仅对权重系数前5的计量性能特征变量进行不确定度分析。

1) 测量流速和体积流量

根据式(1)～式(4),测量流速和测量声速的共同参数包括：各声道长度、声波在各声道的顺流传播和逆流传播的时间。超声流量计参与体积计算的参数包括声道长度、声道角、声波的传播时间以及流通面积。声道长度、声道角以及流通面积均作为流量计内置固定参数,因此对于测量流速和体积流量,其影响因素都可归结为声波传输时间。因此测量流速、体积流量的不确定度主要来源于理论声速的不确定度和声速偏差的不确定度。

2) 理论声速的不确定度

理论声速值是基于温度、压力、组成等数据,根据AGA Report No.10提供的计算公式计算得到理论值[20]。理论声速的不确定度包括计算方法、温度、压力、组分测量的不确定度,因此理论声速计算方法的不确定度取0.09%。

压力测量(1 MPa以上)的标准不确定度为:

ur(p)=0.008 2%～0.057 7%

(9)

温度测量的标准不确定度：

ur(T)=0.005 0%

(10)

组分含量的标准不确定度(参照一级标准气体)：天然气中各组分含量由色谱分析仪测量得到,其不确定度由色谱分析仪测量结果的重复性和标准物质各组分含量的不确定度量部分组成。

天然气一级标准气体中甲烷为平衡气。天然气中乙烷、丙烷和二氧化碳含量的相对标准不确定度ur(xm)为0.25%;其他组分的ur(xm)为0.5%。

气体标准物质中甲烷含量x1由气体总含量(100%)扣除全部少量组分含量后得到：

(11)

式中：x1为甲烷组分含量;xm为天然气中除甲烷外第m组分含量,m=2～11。

对气体标准物质中甲烷含量的标准不确定度u2(x1)进行评定。根据不确定度传播定律,u2(x1)可由各少量组分的标准不确定度u2(xm)分量合成得到：

(12)

式中：u2(x1)为甲烷组分含量的标准不确定度;u2(xm)为天然气中除甲烷外第m组分含量的标准不确定度。基于标准物质中甲烷含量的标准不确定度及甲烷含量,可计算得到组分测量的相对标准不确定度ur(M)=0.013%。

理论声速的不确定度计算结果如表5所示。

表5 理论声速的不确定度

3) 声速偏差不确定度

测量声速是通过测量声波在已知长度的路径上传播时间,计算得到声波在气体中的实际传播速度,与理论声速的测量原理不同。因此需要评估测量声速与理论声速间偏差的不确定度。

超声流量计各声道间的偏差不超过0.035%,视其在变化界限内为均匀分布,各声道间声速测量偏差带来的不确定度为：

(13)

在10 MPa压力范围内,超声流量计声速偏差小于0.06%。认为其在变化界限内为均匀分布,测量平均声速与理论声速间偏差带来的不确定度为：

(14)

则声速偏差带来的不确定度为：

(15)

理论声速不确定度和声速偏差的不确定度合成得到测量流速、体积流量的不确定度为：

(16)

4) 流量测量不确定度

超声流量计流量测量的不确定度需要考虑被检表流量测量、测量重复性及温度、压力、压缩因子等的不确定度。

基于质量守恒,被检表处测量得到的体积流量为：

(17)

式中：qv,MUT为被检表测量得到的体积流量;qf为标准装置中标准表测量得到的体积流量;p为标准表处的压力;pMUT为被检表处的压力;T为标准表处的温度;TMUT为被检表处的温度;Z为流经标准表的介质气体的压缩因子;ZMUT为流经被检表的介质气体的压缩因子。

实际计算中,温度、压力及压缩因子带来的不确定度较小,可以忽略。因此超声流量计流量测量的不确定度为：

(18)

式中：ur(qv,MUT)为被检表流量测量的不确定度;uR(qf)为超声流量计流量测量的重复性。实流标准装置中被检表流量测量的扩展不确定度为0.16%,超声流量计流量测量重复性取最大值0.08%,超声流量计流量测量的不确定度为：

(19)

4台超声流量计的输入变量的标准不确定度、权重系数的范围如表6所示。结合特征变量的权重系数,计算得到模型输入变量的合成不确定度。

表6 输入变量标准不确定度及权重系数Tab.6 The standard uncertainty and weight coefficient

模型输入变量的合成标准不确定度为：ur,var=0.093%～0.048%;扩展不确定度为：Ur,var=0.19%～0.10%(k=2)。

4.3.3 预测结果的不确定度

预测结果的标准不确定度u包括测量带来的不确定度,即：输入变量的不确定度ur,var以及算法模型本身的不确定度ur,fit可表示为：

(20)

计算得到4台流量计的流量偏差预测结果的标准不确定度如表7所示。

表7 预测结果的标准不确定度

根据4台超声流量计的预测结果,可得到基于机器学习算法的超声流量计使用中检验方法的扩展不确定度范围为：U=0.92%～0.22%(k=2)。

5 结 论

本文通过建立基于随机森林算法的超声流量计流量偏差预测分析模型,保证超声流量计使用中的准确度,实现了对超声流量计的使用中检验。得到的主要结论：

1) 建立超声流量计使用中检验程序,通过获取超声流量计信号质量、流态指标、计量性能等变量,对超声流量计使用中的性能进行分析判断。

2) 建立基于随机森林算法的超声流量计的流量偏差预测模型,并分析影响超声流量计使用中准确度的变量。评估预测结果的不确定度,完成对超声流量计使用中检验方法的完整评估。

本文的研究结果能够为超声流量使用中检验方法的推广和应用提供依据。此外,基于随机森林算法的预测模型建立,不仅能够保证超声流量计工作中的准确度,也可为超声流量计在线校准方法的研究提供支撑。在未来的研究中,将进一步完善超声流量计使用中检验程序,建立具有更强适应性的机器学习算法模型和评估系统,保证使用中超声流量计的准确度。