基于相似日和相关性加权的特高压变压器顶层油温预测研究
2022-02-01谭风雷
谭风雷,陈 昊
(1.国网江苏省电力有限公司超高压分公司,南京 211102; 2.国网江苏省电力有限公司南京供电分公司,南京 210019)
0 引 言
特高压变压器是电力系统的核心设备,其健康状态影响系统的稳定。针对特高压变压器而言,绕组热点温度(简称为“绕温”)是表征特高压变压器绝缘状况的核心参数[1-3],然而绕温直接测量较为困难且成本较高,而顶层油温测量简单,且与绕组热点环境温度具有较大相关性,故变电站运行人员一般采用顶层油温代替绕组热点环境温度来评估绝缘状况[4-6]。若能提前预测特高压变压器油温,即可预判特高压变压器绝缘状况,有利于延长使用寿命。
目前,国内外专家学者对变压器绕温和顶层油温预测方法进行了大量研究,主要包含有限体积法、人工智能算法等。文献[7]基于有限体积法,结合系统边界条件,计算得到变压器绕温分布,并通过现场测试验证了算法的可行性。文献[8]利用油温-绕组等效热路模型,提出一种变压器绕组热点环境温度分析方法,采用变压器实时负荷和顶层油温数据,在线分析绕组热点环境温度,文献[9]提出一种基于优化混合核极限学习机的变压器油温预测方法,充分考虑了变压器油温的各类影响因素,并通过粒子群优化了混合核极限学习机,提高了变压器油温预测精度。而针对特高压变压器油温预测研究的文献甚少。
在数据预测领域,短期预测方法[10-12]主要有时间序列法、趋势变化法、人工智能算法和相似日法等。考虑到相似日法不仅算法简单,且大量应用到负荷预测、风电预测等电力领域,因此采用相似日法预测特高压变压器油温,通过合理选择相似日,即可提高油温预测精度。
该文提出基于实际油温和油温变化率的2种气象相关度模型,并在充分研究时间和负荷相关度模型之后,建立了基于Topsis法的综合相关度模型。根据气象相关度模型和综合相关度模型,选择得到2种相似日集合,并分别采用支持向量机和油温求导法,基于相关性加权实现特高压变压器油温预测。在详细给出计算步骤的基础上,通过分析计算江苏某特高压变压器主体变油温数据验证该方法的可行性。
1 各因素相关度模型建立
采用相似日法预测特高压变压器油温,首先计算待预测样本日各类因素与历史样本各类因素的整体相关度[13]。考虑到特高压变压器油温受影响因素较多,结合现场实际情况,在计算相关度时,将重点研究气象、时间和负荷等3种因素。
1.1 气象相关度模型
研究气象相关度时,重点分析环境温度、环境湿度、风速等级和大气压力等4种因素。设Ti为待预测样本日前第i天环境温度对应的向量,Hi为待预测样本日前第i天环境湿度对应的向量,Ui为待预测样本日前第i天风速等级对应的向量,Pi为待预测样本日前第i天大气压力对应的向量,则
(1)
式中:Tij为待预测样本日前第i天j时刻对应的环境温度实际值;Hij为待预测样本日前第i天j时刻对应的环境湿度实际值;Uij为待预测样本日前第i天j时刻对应的风速等级实际值;Pij为待预测样本日前第i天j时刻对应的大气压力实际值;N为实际样本数量。
计算气象相关度前,先定义归一化模型:
(2)
式中:X为中间变量;CX为归一化系数,一般取值为0~0.05。
基于4种气象因素,构建整体气象因素Zij:
Zij=af(Wij)+bf(Sij)+cf(Fij)+df(Qij)
(3)
式中:a、b、c、d分别为环境温度、环境湿度、风速等级以及大气压力的占比。则待预测样本日前第i天对应的整体气象因素向量Zi为
Zi=[Zi1,Zi2,…,Zij,…,Zi23,Zi24]
(4)
设待预测样本日前第i天特高压变压器对应的实际油温向量Ti为
Ti=[Ti1,Ti2,…,Tij,…,Ti23,Ti24]
(5)
式中:Tij为待预测样本日前第i天j时刻特高压变压器对应的实际油温值。
利用Zi和Ti,可得Rj:
Rj(a,b,c,d)=
(6)
式中:Rj为所有样本内j时刻整体气象因素与实际油温对应的相关度。
当式(6)中Rj取得极大值,此时对应的a1j,b1j,c1j,d1j,即为j时刻4种气象因素的最优占比:
Rj(a1j,b1j,c1j,d1j)=max[Rj(a,b,c,d)]
(7)
此时,第j时刻4种气象因素的加权值可以表示为
(8)
式中:w1Tj、w1Hj、w1Uj和w1Pj分别为j时刻环境温度、环境湿度、风速等级和大气压力的相关度加权系数。则基于实际油温的待预测样本日前第i天与待预测样本日的气象因素相关度模型M1i可以表示为
(9)
式中:RTi、RHi、RUi和RPi分别为待预测样本日前第i天与待预测样本日环境温度、环境湿度、风速等级和大气压力的相关度,计算方法见式(6)。
研究基于油温变化率的气象因素相关度M2i。先定义油温变化率函数为
(10)
式中:TFij为待预测样本日前第i天第j时刻的油温变化率。则待预测样本日前第i天油温变化率对应的向量TFi为
TFi=[TFi1,TFi2,…,TFij,…,TFi23,TFi24]
(11)
根据M1i,同理可得M2i,表达式如下:
(12)
式中:w2Tj、w2Hj、w2Uj和w2Pj分别为基于油温变化率的j时刻环境温度、环境湿度、风速等级和大气压力的相关度加权系数。
1.2 时间相关度模型
考虑到距离待预测样本日越近,时间相关度越高,反之距离待预测样本日越远,时间相关度越低,本文建立待预测样本日与历史样本的时间相关度模型[14-15]如下:
(13)
式中:Fi为待预测样本日与待预测样本日前第i天的相关度;k1和k2为时间系数,一般取值为0.85~0.99;floor(i/7)为对i/7向下取整;mod(i/7)为对i/7取余。
1.3 负荷相关度模型
考虑到在同等条件下,特高压变压器负荷越大,油温越大,反之特高压变压器负荷越低,油温越小,本文建立待预测样本日与历史样本的负荷相关度模型[16-17]如下:
(14)
式中:Pix为待预测样本日前第i天第x时刻的负荷;P0x为待预测样本日第x时刻的负荷。
2 基于Topsis法的综合相关度模型建立
根据气象、时间和负荷3种因素相关度模型,结合Topsis法建立综合相关度模型。先确定正理想解和负理想解,考虑到选择相似日时,气象、时间和负荷3种因素相关度越大越好,则正理想解和负理想解可以表示为
(15)
设待预测样本日前第i天气象、时间和负荷3种因素向量表示成Ri=(Mxi,Ti,Li)(x=1,2),根据欧氏距离可得Ri与R+的距离为
(16)
同理可得Ri与R-的距离为
(17)
设Ri与R+的近似度SCxi为
(18)
建立待预测样本日与历史样本的综合相关度模型如下:

(19)
3 特高压变压器油温预测方法研究
3.1 相似日集合选择
根据综合相关度,从历史样本中选择相似日集合。考虑到文中建立了2种气象相关度模型,因此在选择相似日集合时,将分开讨论,具体方法如下(见图1)。

图1 相似日集合选择的流程图
1)从N个历史样本中选择综合相关度C1i最大的20个样本作为相似日备选集合1,再从相似日备选集合1中选择基于实际油温的气象相关度M1i最大的10个样本作为相似日集合1。
2)从N个历史样本中选择综合相关度C2i最大的10个样本作为相似日备选集合2,再从相似日备选集合2中选择基于油温变化率的气象相关度M2i最大的5个样本作为相似日集合2。
3.2 特高压变压器油温预测
相似日集合选择后,下面介绍特高压变压器油温预测方法。考虑到相似日集合1是基于实际油温的气象相关度选择的,因此该集合选择支持向量机预测特高压变压器油温。利用相似日集合1样本的环境温度、环境湿度、风速等级和大气压力4种气象因素作为支持向量机的输入向量,对应的油温作为支持向量机的输出向量,训练支持向量机,借助训练好的支持向量机[18]即可预测特高压变压器油温PY1j。
同时考虑到相似日集合2是基于油温变化率的气象相关度选择的,因此该集合选择油温求导法预测特高压变压器油温。利用相似日集合2中样本的油温变化率平均值作为待预测样本日油温变化率,借助油温求导法预测特高压变压器油温PY2j。
根据基于支持向量机的预测结果和基于油温求导法的预测结果,利用相关性加权原理即可得到特高压变压器油温的预测结果PYj,其表达式如下:
(20)
式中:a为相似日集合1中样本集;b为相似日集合2中样本集。
根据特高压变压器油温预测步骤,给出了特高压变压器油温预测的流程图,如图2所示。
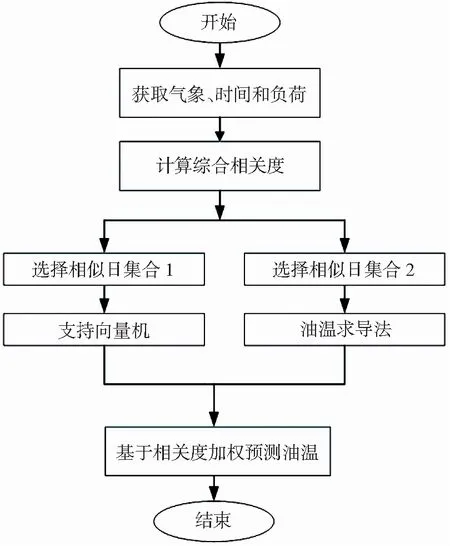
图2 油温预测的流程图
4 算例分析
采用江苏某特高压变压器主体变2018年7月、8月油温作为研究对象,来验证油温预测方法的有效性,其中样本数量N设为30。
4.1 气象相关度模型分析
以江苏某特高压变压器主体变2018年7月31日作为待预测样本日,分析该日前30天的气象相关度。根据气象相关度模型,可得4种气象因素的加权值如表1和表2所示。
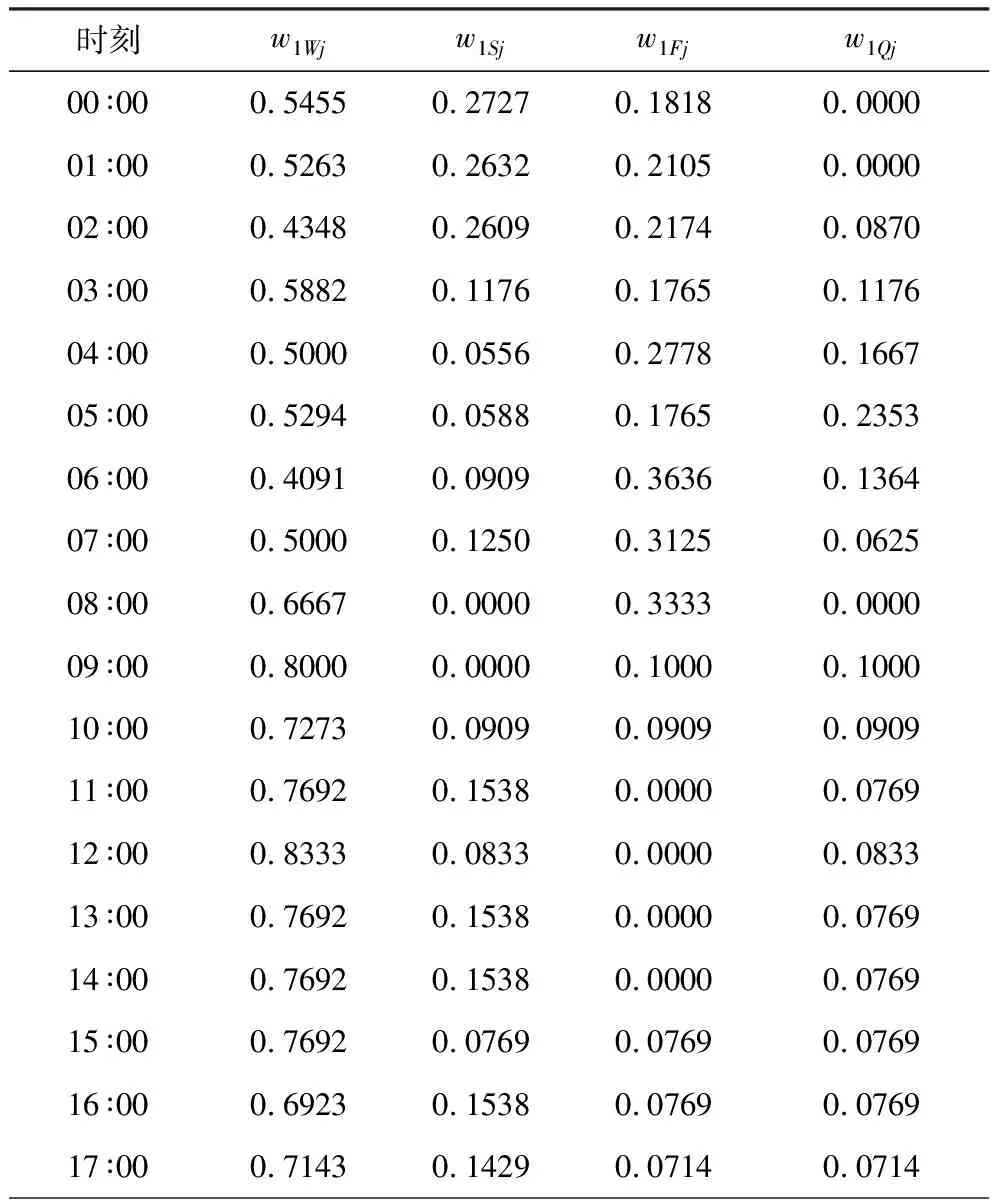
表1 基于实际油温的4种气象因素加权值
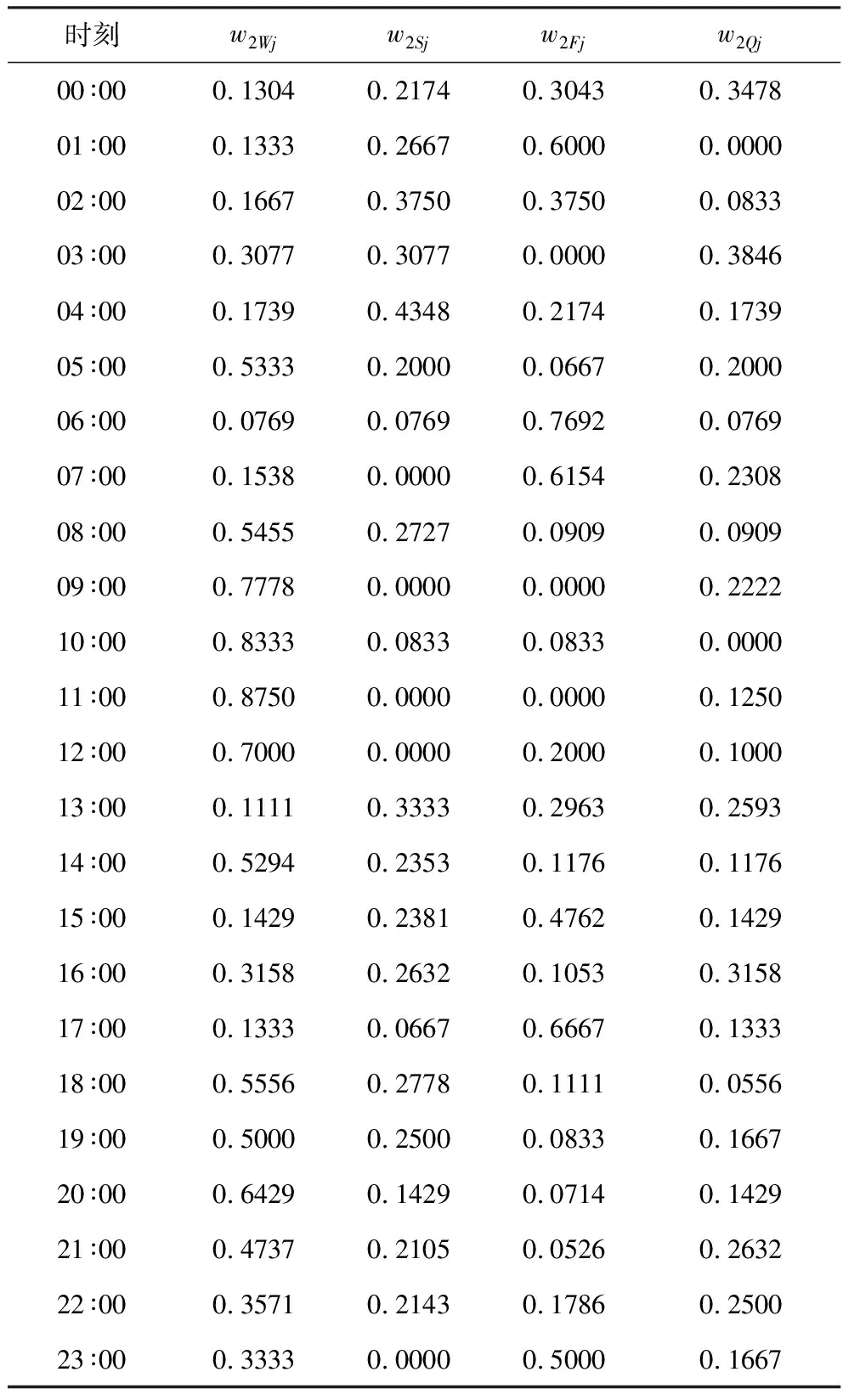
表2 基于油温变化率的4种气象因素加权值
分析表1和表2可知:环境温度、环境湿度、风速等级和大气压力4种气象因素在不同时刻对应的加权值不同,其中环境温度因素加权值最大。根据4种气象因素加权值,绘制气象相关度曲线,如图3和图4所示。
分析图3和图4可知:不管是基于实际油温的气象相关度,还是基于油温变化率的气象相关度,都与时间无关,是随机变化的。

图3 基于实际油温的气象相关度曲线

图4 基于油温变化率的气象相关度曲线
4.2 综合相关度模型分析
分析综合相关度模型前,先设时间系数k1为0.88,k2为0.98。根据式(19)可得综合相关度曲线,如图5和图6所示。
分析图5和图6可知:基于实际油温的综合相关度曲线与基于油温变化率的综合相关度曲线基本相近。

图5 基于实际油温的综合相关度曲线
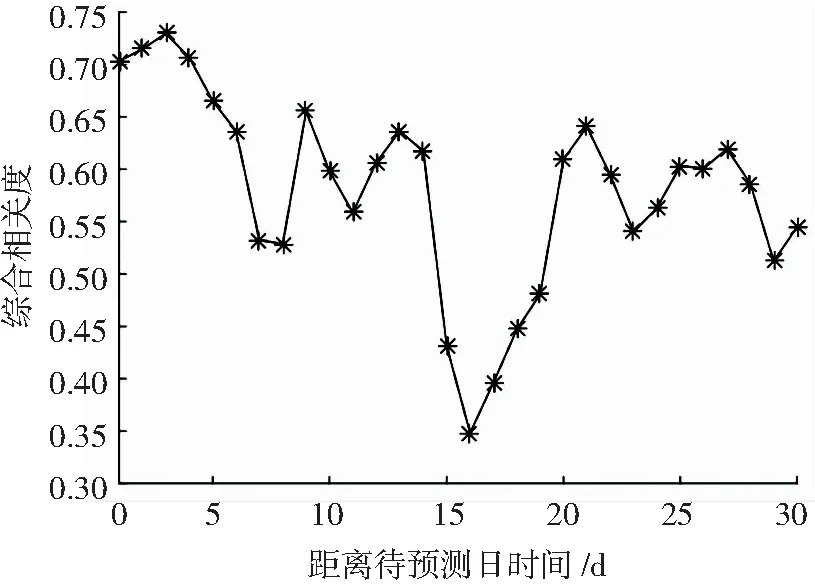
图6 基于油温变化率的综合相关度曲线
4.3 相似日集合选择结果分析
根据综合相关度计算结果,选择待预测样本日的相似日集合,以2018年7月31日为例,其对应的相似日集合选择结果如表3所示。
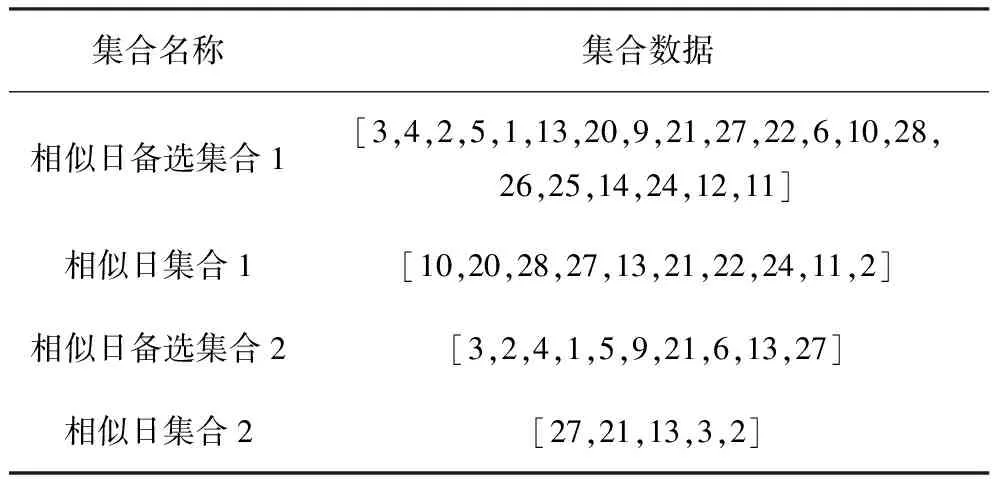
表3 相似日集合
分析表3可知:基于实际油温的综合相关度与基于油温变化率的综合相关度2种方法选择的相似日集合相差较大。
4.4 油温预测结果分析
为验证预测方法的可行性,对江苏某特高压变压器主体变2018年7月31日至8月9日共10天的油温进行预测。其中,相似日集合1采用支持向量机预测,其对应的最佳核函数及相关参数如表4所示。

表4 支持向量机核函数及其参数
相似日集合1采用支持向量机预测,相似日集合2采用油温求导法预测,其各自的预测结果如表5所示。
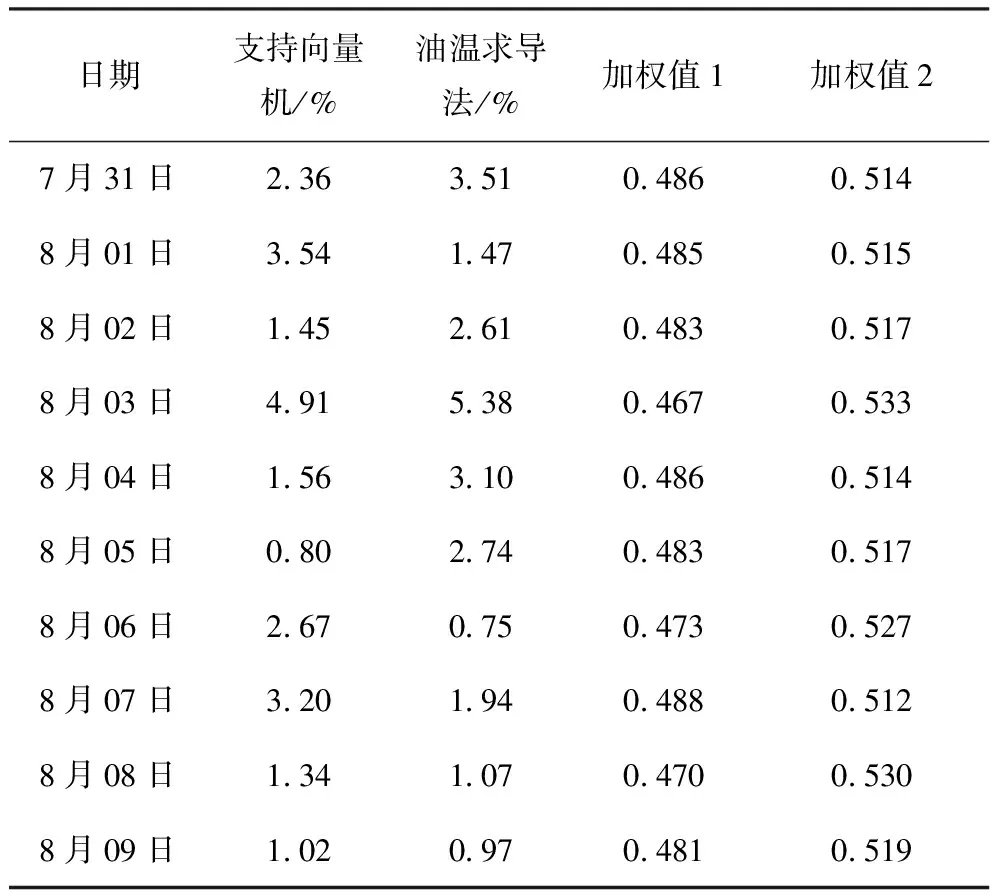
表5 2种方法的预测结果
根据2种方法的预测结果,结合式(20),即可得到所提出的相关性加权的预测结果,如表6和图7所示。分析表6和图7可知:采用相关性加权法的预测效果较好,日平均相对误差为2.02%,日最大相对误差为5.16%,日最小相对误差为0.83%,能够满足特高压变压器油温预测的精度需求。

表6 相关性加权法的预测结果

图7 平均相对误差曲线
为进一步分析,绘制了表7。分析表7可知:相对支持向量机和油温求导法,相关性加权法预测特高压变压器油温的精度更高,从而验证了该方法的有效性。

表7 预测结果对比情况
5 结 语
1)考虑环境温度、环境湿度、风速等级以及大气压力,建立了基于实际油温和油温变化率的2种气象因素相关度模型;同时鉴于特高压变压器油温受时间变化和负荷大小影响较大,又建立了时间和负荷相关度模型。
2)利用气象、时间和负荷3种因素的相关度模型,建立了基于Topsis法的综合相关度模型;根据气象相关度模型和综合相关度模型,选择了相似日集合,并基于支持向量机和油温求导法,建立了基于相关性加权原理的特高压变压器油温预测方法。
3)在详细给出基于相关性加权原理的特高压变压器油温预测方法计算步骤的基础上,以江苏某特高压变压器主体变作为研究对象,分析了相关性加权法的计算过程和预测效果,从而验证了该方法的有效性。
