A*算法在AGV路径规划上的改进与验证

耿宏飞 神健杰

(南京理工大学自动化学院 江苏 南京 210094)

0 引 言

AGV小车凭借自动化程度高、灵活性强、安全性好等特点受到了公司的青睐，特别在环境精度要求高或者特殊环境的行业需求在迅速增长，但与此同时AGV运输路线的规划也成了关键问题[1]。尤其在多AGV、多任务的工作环境下，优良的路径规划方法能够使AGV更快速地处理分配的任务，对于增加客户的满意度、提高仓储货物调度效率减少仓储运行成本、提升企业科技含量和增加企业利润有着至关重要的作用[2]。

路径规划是指在已知起点和终点，所在环境地图存在障碍物的情况下，为控制对象规划一条符合要求的高效且最优路径。常见的路径规划算法有Dijkstra算法、A*算法，此外还包括智能优化算法中的蚁群算法、遗传算法等。A*算法凭借在静态网络中求解路径最短和最有效的优点被广泛使用，但该算法的启发函数采用曼哈顿距离时会出现不必要的局部绕行和较多的转弯次数等问题。文献[3]在启发函数中加入附加因子，有效地提升了启发函数取舍相同值的能力，从而避免绕行和搜索时间的浪费，但该算法应用场景比较单一，对其他场景并不适用。赵江等[4]利用三点共线原理，判断中间节点是否为无用的点，并加以剔除，再利用向量概念，使用两个向量的乘积来判断障碍物与AGV的位置，从而高效快速地绕开障碍物。但这导致规划路径过程中计算过于复杂，无形中增加了运行的时间。文献[5]中针对传统A*算法规划所得路径在安全性与平滑性方面的不足的情况，提出在估价函数中加入安全威胁代价，代价值大小反比于节点与障碍物之间的最小距离，使得规划路径尽可能远离障碍物。这种方法虽然有效地避开了障碍物，但无形中增加了路径总体的长度，使得规划效率降低。于赫年等[6]首先针对采用A*算法规划时AGV不必要转弯过多问题，引入了转向修正概念，在AGV转弯时加入转弯代价k，有效地减少了运行时的转向。其次针对A*算法采用曼哈顿距离接近目标终点时可能出现局部绕行的情况，提出了欧氏距离和曼哈顿距离结合的方法，利用欧氏距离采用对角线定义的特性，有效避免了局部绕行，但此方法只针对距离目标点较近的情况，并不适用于全局规划。

本文在文献[6]加入转弯代价的A*算法的基础上进行改进，针对启发函数采用曼哈顿距离遇到障碍物时，可能出现局部绕行的问题，分别从修改启发函数和几何方法出发，提出采用局部欧氏距离和障碍物端点距离判断方法，仿真结果表明改进算法有效避免了局部绕行，缩短了路径的长度以及减少了AGV路径规划的时间。

1 AGV运行环境建模

经常使用的AGV运行环境表示方法主要有集合地图法、拓扑地图法和栅格地图法等。栅格地图法是当前使用最多的方法之一，本文采用栅格法来建立AGV的运行环境。该方法将AGV的运行区域划分成为多个有序的方格，这些方格叫做栅格。当使用规划算法进行规划时，单位栅格长度表示AGV每走一步的距离，在一个完整路径规划过程中，会将一些栅格连接起来构成一条显式连通图，该连通图表示为规划的路径[7]。栅格地图中不包含障碍物的栅格赋值为0，包含障碍物的栅格赋值为1。栅格地图中的路径易于观察，地图现实的信息与创建初始环境一一对应，并且AGV的定位准确易于修改与创建。

在实际应用场景中，环境较为复杂，为了减少AGV之间的路径冲突，也有利于对A*算法进行改进，本文采用上下左右4个方向的拓展搜索方法。如图1所示，中间带有圆圈方格为当前节点，箭头指向为四个拓展方向。此方法不但稳定可靠而且在多AGV中也易于管理。

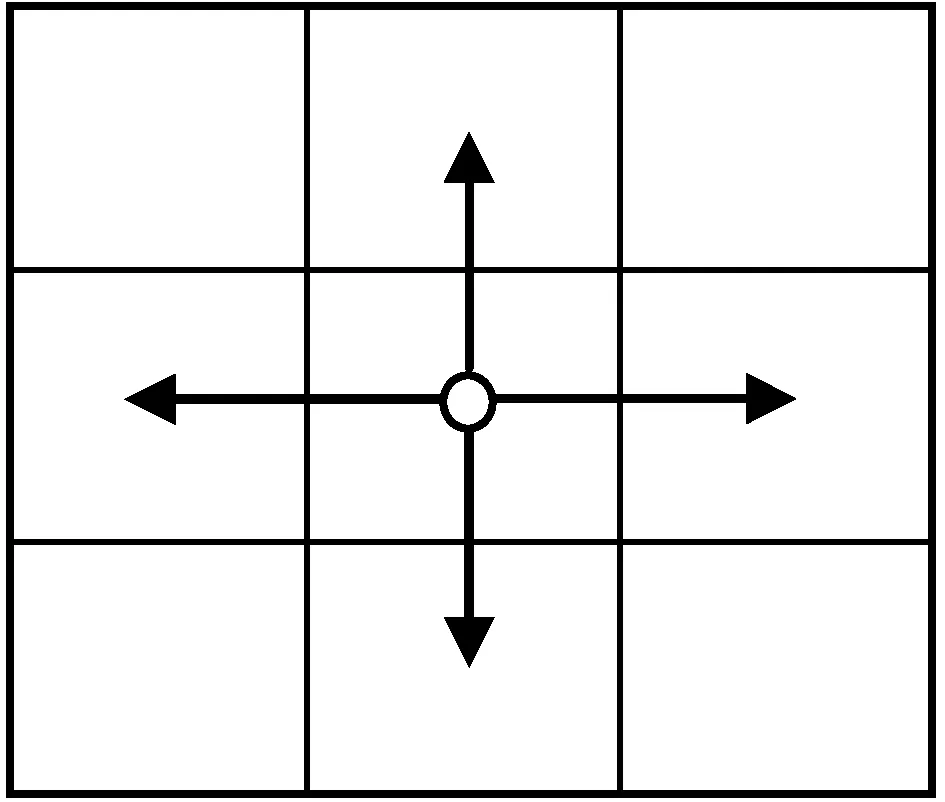
图1 路径规划节点拓展方向

2 A*算法

2.1 基本原理

A*算法是一种启发式算法，是在广度优先算法的基础上引入一个启发函数，与传统深度优先广度优先搜索算法有所区别，在A*算法中，并不是将所有的可遍历的点都进行搜索，虽提高了搜索效率，但不一定是最优的路径。事实上，A*算法在传统搜索算法基础上添加了限定条件，相当于设置了阈值，从而判断舍弃不符合要求的点[8]。下面对A*算法进行介绍。

A*算法如式(1)所示。

f(n)=g(n)+h(n)

(1)

式中：f(n)为起点经当前节点到目标节点的估计距离；g(n)为起点到当前节点的实际距离；h(n)为当前节点到目标节点的估计距离。

A*算法的实现过程中要建立一个open表和一个close表，分别用来存放当前节点周围四个方向的节点以及子节点f(n)和已经搜索过的点。在整个路径规划过程中要对这两个表进行维护，路径规划过程中，将当前节点作为父节点，对此节点上下左右四个节点计算f(n)值，open表功能在于使用优先级队列去选择f(n)值最小的节点，并将其节点放在close表当中，在整个过程中重复此过程，从而规划出距离最小的路径。

在A*算法过程中，为保证找到最短路径(最优解)需要选择合理的函数h(n)。如果选定的h(n)值小于节点n到目标节点F的实际距离值，需要搜索的节点数目较多，搜索范围较大，运算量增加，但能够保证得到的解是全局最优解。若选择h(n)的值大于节点n到目的节点的实际距离值，在求解的过程中，会根据f(n)值舍弃部分节点，加快求解速度，缺点在于最优解可能包含在舍弃的节点，只能保证最后的解是较优解。为求解最短路径，估价函数的取值应尽量接近于实际值[9]。

2.2 加入转弯代价

传统的A*算法主要将长度作为标准，即总长度最短为最优路径。但一味地追求长度最短，将会导致AGV在行驶过程中频繁地转向，而在实际应用中由于转弯会进行加速和减速的过程，时间成本要比直线行驶高出许多，使得整体的效率下降，而且使整体路径不够平滑。针对此问题，其中一个改进策略是在原有的A*算法启发函数上加一项转弯代价k，k为转向所花费的代价。改进后的A*算法如式(2)所示。

f(n)=g(n)+h(n)+k

(2)

在传统A*算法启发函数增加转弯代价，路径的评价不仅仅是路径最短，还要考虑转弯所带来的路径代价，长短仍然是路径规划的关键因素但不是唯一因素[6]。由于A*算法是按照代价最小的原则来规划路线，所以减少一些不必要的转弯，使得路径更加平滑。因此本文中启发函数为曼哈顿距离的A*算法是在加入转弯代价的基础上进行研究与改进。

3 改进A*算法

3.1 局部欧氏距离

A*算法的启发函数通常采用欧氏距离和曼哈顿距离。具体表达式如下：

H(n)=abs(n.x-d.x)+abs(n.y-d.y)

(3)

H(n)=sqrt((n.x-d.x)2+(n.y-d.y)2)

(4)

式中：abs表示求取数值的绝对值；sqrt表示求取数值的正平方根；(n.x,n.y)为当前点的坐标；(d.x,d.y)为目标点的坐标。

A*算法采用两种距离时各有优缺点：曼哈顿距离是根据横坐标和纵坐标绝对值之和来定义的，根据此特性一般可以获得转弯较少的路径，但遇到障碍物时会出现局部绕行的缺点；欧氏距离是根据对角线距离来定义的，根据此特性一般遇到障碍物时不会出现局部绕行，但在路径规划当中会出现转弯较多的情况。本文综合考虑两种距离的优缺点，提出全局使用曼哈顿距离而遇到障碍物使用欧氏距离的方法。

设遇到障碍物的点为A点，障碍物的前一个路径行驶点为B点，前两个路径行驶点为C点，如图2所示。

图2 行驶轨迹与障碍物的位置

设A点坐标为(a.x,a.y)，B点坐标为(b.x,b.y)，C点坐标为(c.x,c.y)。因此向量CB和向量BA分别表示为(b.x-c.x,b.y-c.y)和(a.x-b.x,a.y-b.y)。因为由实际AGV行驶情况可知，向量CB和向量BA只有垂直与水平两种位置情况。利用两个向量夹角θ的余弦值来表示两个向量的位置关系。垂直和水平两种位置情况对应的余弦值分别为0和1。

当余弦值为1时，表明向量CB和向量BA是水平的，此时AGV的运动轨迹与障碍物是垂直关系，那表明此时AGV刚好遇到障碍物，此时应将A*算法的启发函数改为欧氏距离进行路径规划，以免使用曼哈顿距离导致局部绕行。因为本文方法只在运动轨迹与障碍物为垂直关系时使用欧氏距离，所以使用欧氏距离时不需要加入转弯代价。

当余弦值为0时，表明向量CB和向量BA是垂直的，此时AGV的运动轨迹与障碍物是水平关系，那表明此时AGV沿着障碍物水平行驶，A*算法仍然继续使用曼哈顿距离进行路径规划。

同理此方法也适用于障碍物垂直放置的情况。加入局部欧氏距离的改进A*算法执行流程如图3所示。

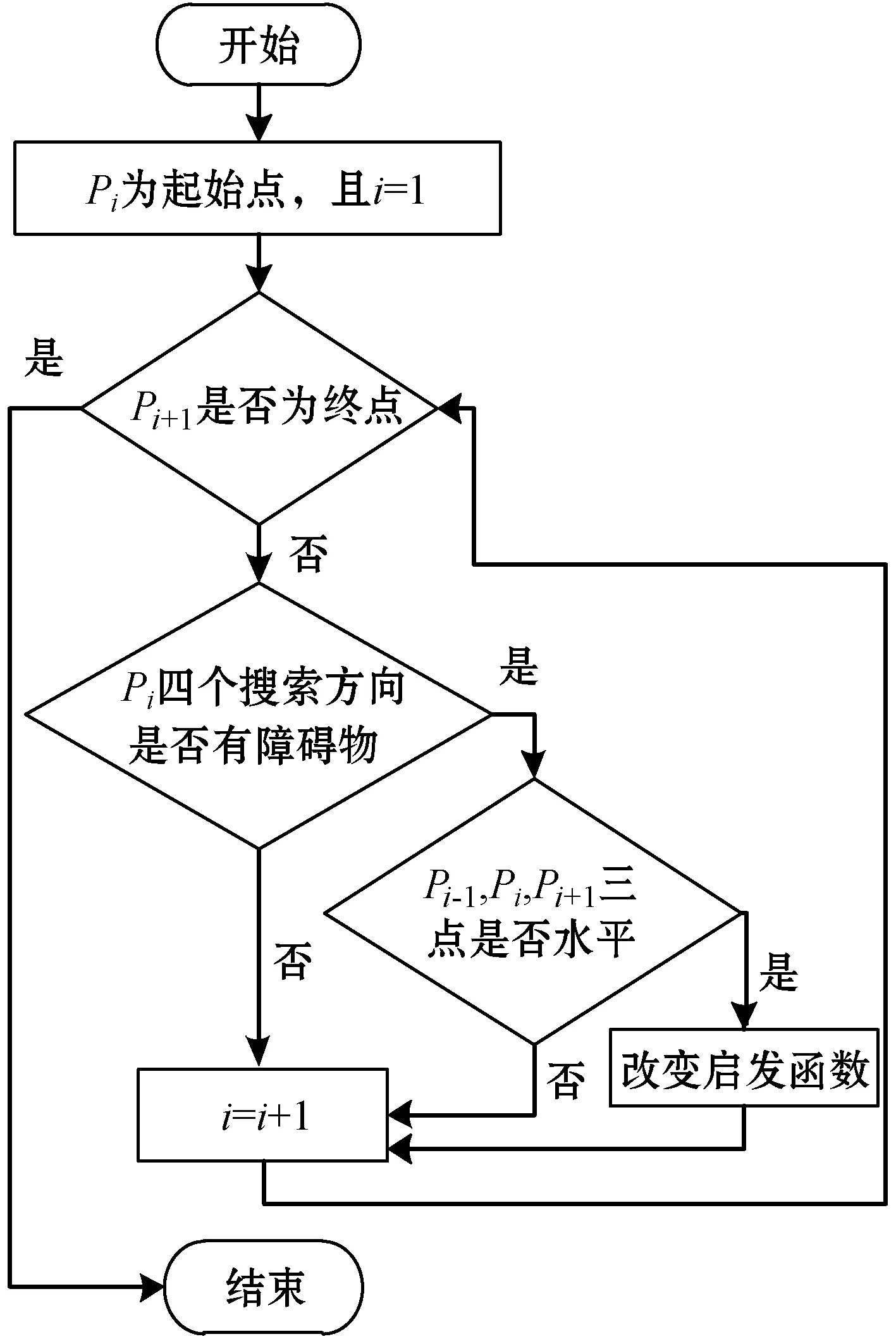
图3 加入局部欧氏距离的改进A*算法执行流程

3.2 障碍物端点距离判断

本节解决的AGV路径规划同样是3.1 节所针对的问题：AGV在进行路径规划过程中，当前点的四个搜索方向存在障碍物。与3.1节有所不同的是，无论向量CB和向量BA垂直或者水平，A*算法的启发函数为曼哈顿距离保持不变；但在两个向量水平时要进行当前点与障碍物两段点的几何判断，如图4所示。

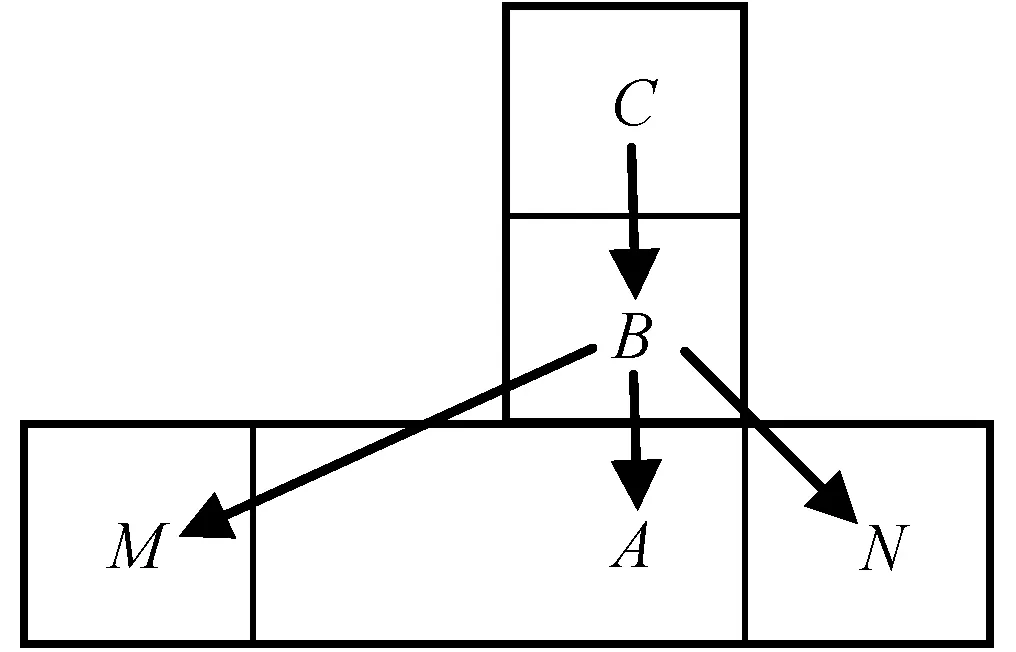
图4 当前点与障碍物两段点的几何判断

M、N点分别为障碍物第一排几何最左端、最右端的点，坐标分别为(m.x,m.y)和(n.x,n.y)。此时通过比较B点到M点的距离和B点到N点的距离的大小，即可得出B点更靠近障碍物左端还是右端。

B点到两点的距离可以表示为|BM|和|BN|。具体表达式如下：

(5)

(6)

当|BM|大于|BN|时，表示B点更靠近障碍物右端，此时规定A*算法的规划方向为向右，从而避免障碍物局部绕行。当|BM|小于|BN|时，表示B点更靠近障碍物左端，此时规定A*算法的规划方向为向左，从而避免障碍物局部绕行。

同理此方法也适用于障碍物垂直放置的情况，不同的是改变AGV运动方向向下或者向上。加入障碍物端点距离判断的改进A*算法流程如图5所示。

图5 加入障碍物端点判断的改进A*算法流程

4 仿真验证

本文的仿真平台为MATLAB R2017a，并在Windows 10×64位操作系统下进行，AGV的运行环境采用25×25的栅格地图。这里将(2,3)作为起点、(16,21)作为终点。如图6和图7所示，白色为起点和终点，浅灰色为AGV的行驶轨迹，深灰色为障碍物。

图6 加入转弯半径的A*算法

图7 本文改进的A*算法

图6为添加转弯代价的A*算法，可以看出在整个路径规划过程中，AGV的转弯次数为8次，搜索的点数为42个，虽然与传统A*算法相比，转弯次数有所减少，路径上搜索的点数也减少许多，路径相对平滑，性能在一定程度上有所提高。但遇到障碍物时，由于曼哈顿距离本身的弊端，导致不能以最优路径经过障碍物。特别是在障碍物比较密集的地方，例如图中靠近目标点的区域，比其他区域更容易发生不必要的绕行。图7为本文改进的两种A*算法仿真结果，由于遇到障碍物时，两种算法都是按照最短距离避开障碍物的，所以两种算法的仿真结果一致。可以看出，AGV在整个路径规划过程中转弯次数为6次，搜索的点数为38个，与仅添加转弯代价的A*算法相比，转弯次数减少2次，搜索点数减少了4个，特别在遇到障碍物时，本文改进的A*算法经过改变启发函数和判断几何距离的方法能够在行驶过程中对障碍物进行实时判断，有效避免对障碍物不必要的绕行，从而提高了A*算法在路径规划上的搜索效率和性能，减少了AGV的运行时间。表1为添加转弯代价的A*算法与本文两种改进的A*算法的路径规划仿真数据。

表1 加入转弯代价A*算法与本文两种改进A*算法的仿真数据

可以看出，本文两种改进的A*算法在路径长度和转弯次数这两方面上与加入转弯代价的A*算法相比减少9.52%和25.00%。而在运行时间方面，障碍物距离判断的A*算法与加入转弯代价的A*算法相比减少了7.38%，而局部欧氏距离的A*算法则减少了10.26%。这是由于每次遇到障碍物时，障碍物端点距离判断的A*算法在遇到障碍物时，由于几何距离的计算和比较，自然花费的时间会比局部欧氏距离的A*算法花费时间多一点，导致整体路径规划时间要稍微多一些，性能也略逊一筹。因此障碍物端点距离判断的A*算法主要适用于障碍物比较少的情况，规划路径的性能与局部欧氏距离的A*算法相当。

因此对以上仿真结果的分析和比较可以得出本文两种改进A*算法能够克服启发函数采用曼哈顿距离遇到障碍物时局部绕行的缺点，有效减少全局路径规划的长度和转弯次数，从而使路径规划的效率更高。

5 结 语

本文在采用栅格地图法构建AGV的运行环境的基础上，针对启发函数采用曼哈顿距离的A*算法对单AGV路径进行规划遇到障碍物时会出现局部绕行问题，提出两种改进的A*算法：(1)在遇到障碍物时将A*算法的启发函数换为欧氏距离，利用欧氏距离的特性解决绕行问题；(2)通过比较当前点到障碍物两端的距离，确定AGV的行驶方向，从而局部绕行。通过仿真结果及对比可以看出，由于有效避免了遇到障碍物时的局部绕行，两种改进的A*算法有效地减少了路径长度和转弯次数，从而提高了A*算法在路径规划上性能。