一种实值深度置信网络在人体血压预测中的应用

宋 波 刘少阳 衣 鹏 冯云霞

(青岛科技大学 山东 青岛 266100)

0 引 言

高血压是我国乃至世界发病率最高的慢性病之一，它的发生往往会并发心肌梗死、心力衰竭、脑出血等一系列心脑血管疾病，严重危害人体健康。虽然高血压患病几率高、发病危害大、难以根治，但其仍然属于可控疾病。文献[1]指出：高血压患者可以通过服用降压药物、生活方式干预等途径降低血压水平，进而减少高血压及其并发症的发病几率，提高患者的生存质量。

人体血压水平不仅与用药策略和生活方式有关，还受其他因素影响，如季节、温度等环境因素，年龄、BMI指数及腰围等生理指标因素。将影响血压水平的多方面因素纳入人体血压预测模型中，定量分析相关因素对于血压未来变化的影响，有助于提高人体血压预测的准确性，并且血压预测模型的建立还可以辅助医师为高血压患者及高危人群制定个性化的降压策略，预测患者采取降压策略一个随访周期后的血压水平，对于高血压疾病的控制具有重大现实意义。

1 相关工作

现阶段对于血压预测的研究主要分为两个方向，一种是狭义上的，即实时预测，通过挖掘血压与某些人体生理信号之间的关联关系，从而获得更加准确的人体血压水平值；另一种是广义上的，即对未来血压进行预测，根据影响血压的相关因素数据预测血压的未来值，构建血压与其相关影响因素之间的关系模型。

在实时预测中，研究者们通常采用脉搏传导时间(Pulse Transit Time，PTT)、心电图(Electrocardiogram，ECG)、光电容积脉搏波(Photoplethysmograph，PPG)，以及血压仪示波等人体生理信号为基础实现血压预测。如文献[2]采用长短期记忆神经网络模型根据PTT数据预测得到收缩压和舒张压的值；文献[3]通过小波神经网络算法将PPG信号重建成完整的血压波形的方式获得收缩压和舒张压；文献[4]以血压仪示波信号作为输入，通过深度波尔兹曼机学习示波信号与人体血压之间复杂的非线性关系;文献[5]将PPG和ECG数据作为输入，应用支持向量机模型进行血压预测。以上研究均需借助医学设备获取相关的人体生理指标来实现对血压的实时预测，通常用于血压的辅助测量，并不具备提前预测的能力。

目前，对于未来血压预测的研究还相对较少，大部分工作只涉及单一方面的影响因素。如文献[6]提出了一种基于遗传算法优化的贝塔分布模型，用以预测随着持续用药时间的增加人体收缩压的变化曲线；文献[7]根据血压值的历史数据，采用多模糊函数模型来预测人体平均动脉血压；文献[8]以BMI指数、年龄、饮酒情况及吸烟情况等血压影响因素作为输入，通过BP神经网络和径向基神经网络构建人体血压预测模型。以上方法分别从用药情况、历史数据、生活习惯等不同方面出发进行血压预测，未能充分考虑血压是由多方面因素共同影响的结果，预测准确度方面也有较大的提升空间。

针对当前血压预测方法中存在的问题，本文提出一种基于RDBN的人体血压预测模型。该模型由多个GG-RBM单元和一层线性神经网络组成，是一种接受实数型数据输入，返回实数型输出的深度网络模型。模型采用无监督与有监督混合学习的方式，在无监督阶段，通过多个GG-RBM单元组成的深层结构进行连续的非线性变换获得血压相关数据的最优低维表示。在有监督阶段，通过线性神经网络获得血压预测值，根据血压预测值与真实值的误差进行网络参数的有监督微调，并采用Adam算法加速这一过程。

2 基于RDBN的人体血压预测模型

2.1 RDBN网络整体架构

传统DBN网络[9]由多个伯努利-伯努利结构的受限波尔兹曼机(Bernoulli-Bernoulli Restricted Boltzmann Machine，BB-RBM)单元组成，其只能接受二值型的输入，但实际血压影响因素中包括实值类型的数据，使用传统结构难以实现血压数据的特征学习。针对该问题，本文采用将原双层伯努利结构连续化为高斯结构的GG-RBM单元组建成的RDBN网络构建血压预测模型。不仅能够克服传统结构中输入仅可为二值型数据的局限，还将输出连续化，减少了模型提取连续型数据特征时所产生的误差，提高了网络整体的泛化能力。

本文所提出的血压预测模型结构如图1所示，包含一个输入层、多个隐藏层和一个输出层。输入层接受影响血压水平的相关因素数据；隐藏层通过逐层非线性变换，自动弱化与未来血压相关性小的输入因子，强化对未来血压影响大的输入因子权值，形成影响未来血压的相关因素数据的最优低维表示；输出层将隐藏层特征提取的结果作为输入，通过线性激活函数映射得到人体血压的预测值。

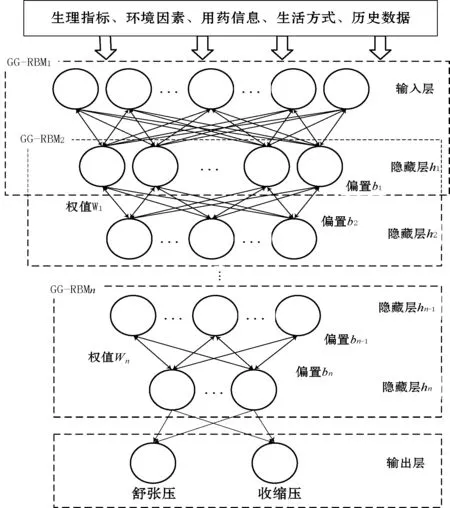
图1 血压预测模型的网络结构

2.2 无监督学习阶段

如图2所示，无监督学习是RDBN网络内部GG-RBM单元从上至下依次进行无监督预训练的过程。本文提出的基于RDBN的血压预测模型能够通过这一过程自动地完成对作用于未来血压相关因素的特征学习，不需要人为设计和参与较为复杂的血压影响因素的特征过程。

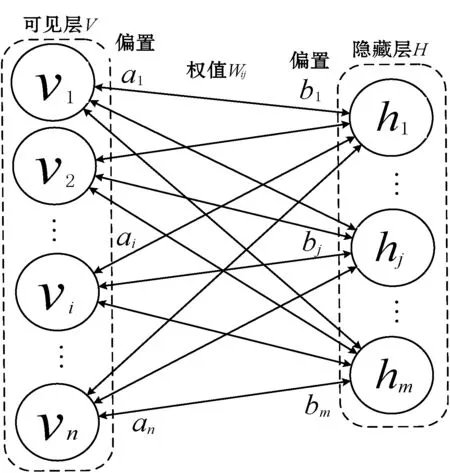
图2 GG-RBM结构

本文采用的GG-RBM单元与传统RBM[10]的区别就是在可见层和隐藏层加入高斯噪声使输入、输出为[0,1]区间的实值类型，故其能量关系函数可表示为：

(1)

式中：θ=[wij,ai,bj]表示需要通过训练求解的参数空间；c是高斯函数中的标准方差。根据能量函数，GG-RBM单元可见层和隐藏层之间的条件概率函数同样服从高斯分布，可分别表示为：

(2)

(3)

对于上述GG-RBM单元，本文采用对比散度(Contrastive Divergence，CD)[11]算法实现快速训练，求解参数空间θ的最优解。由于高斯噪声的引入，相应修改隐藏层神经元的状态信息、可见层神经元重构状态信息和隐藏层神经元重构状态信息分别表示为：

(4)

(5)

(6)

式中：σ表示Sigmoid函数。

根据重构信息与原始信息之间的差值，更新参数空间θ，将上一个单元的输出作为下一个单元的输入，逐层完成整个网络的预训练。从能量关系的角度看，整个预训练过程实际上就是求解使得每个GG-RBM单元能量最低的参数空间θ的过程，单元中蕴含能量越低，表示该状态越稳定，其出现的概率也越大。因此，当预训练完成时，即获得了由影响未来血压的相关因素组成的原始输入向量至最后一层隐藏层的最优非线性映射。

2.3 有监督学习阶段

无监督学习阶段完成时，即完成了参数空间θ的初始化。还需根据血压的实际值与模型的预测值之间的差值对整个RDBN的网络参数进行有监督微调,使其收敛至全局最优点[12]。为衡量模型预测与实际数据之间的差距程度，本文将血压的预测值与实际值之间差值的平方和作为模型的损失函数，其表达式为：

(7)

式中：n表示训练样本容量;youtput,i和yfact,i分别表示第i个样本血压的预测值和真实值。

通常采用梯度下降(Gradient Descent，GD)[13]算法完成深层网络的参数寻优，使模型的损失函数取得极小值。但该方法对于网络中的各参数使用的是相同的学习率，不仅影响梯度下降的效率，还容易陷入局部最优。故本文基于能为不同参数设计自适应性学习率的Adam算法[14]设计梯度下降过程，加速人体血压预测模型的有监督学习。该算法能根据梯度的一阶矩估计和二阶矩估计微调网络，参数的更新规则如下：

(8)

式中：mt和vt分别表示第t次迭代参数梯度的一阶矩估计和二阶矩估计;ε是一个用于防止分母为0的极小常量;α表示网络权重更新的步长因子。

虽然Adam算法能根据梯度的矩估计实现步长因子的自动退火，但步长因子α的设置仍会影响网络最终的收敛状态[14]，当其初始值设置较大时，可能会导致梯度下降过程中直接跳过最优点，造成模型的欠拟合；当其初始值设置较小时，收敛速度又无法保证，容易造成过拟合。因此，本文在每次迭代过程均对步长因子α进行衰减处理，规则如下：

(9)

式中：t表示迭代次数。基于优化步长因子的Adam算法进行梯度下降过程，能够让网络参数的更新过程更加平稳，避免了由于步长因子过大导致的损失函数震荡，提高了人体血压预测模型有监督学习的效率。

2.4 人体血压预测流程

本文构建的RDBN网络模型对于人体血压预测的流程如图3所示，具体步骤如下。

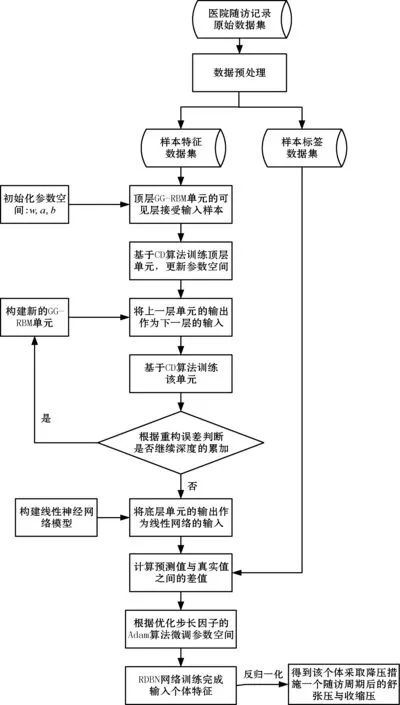
图3 人体血压预测流程

(1)以医院高血压随访记录作为原始数据集，进行数据的预处理，将影响未来血压的相关因素数据归一化，形成未来血压影响因素的样本特征数据集：

(10)

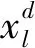
Y=[y1,y2,…,yl,…,yL]T

(11)

式中：yl表示第l条样本数据所对应个体由舒张压和收缩压组成的二维向量。人体血压预测模型就是为了构建从样本特征数据集X到样本标签数据集Y的映射关系。

(2)层层堆叠GG-RBM单元组成深层网络，根据重构误差[15]确定网络的深度。将步骤(1)中处理好的样本特征数据集作为第一个GG-RBM单元的输入，从上至下进行无监督的逐层训练，得到人体血压预测模型网络参数的初始值。

(3)构建线性神经网络与步骤(2)中底层GG-RBM单元的隐藏层相连，将隐藏层的输出作为线性神经网络的输入，根据线性网络的输出值与对应样本标签数据之间的差值，通过优化步长因子的Adam算法迭代更新人体血压预测模型的网络参数。

(4)参数空间更新完成后，给定某个体的一组输入数据后，可以得到该个体采取降压措施一个随访周期过后的血压情况。

3 实验与结果分析

3.1 实验数据与实验环境

实验数据采集自某市160多家社区服务基层卫生中心2014年8月至2017年4月对于高血压患者及高危人群的追踪随访记录，选择其中数据完整的80 162条记录作为本文的实验数据。将同一患者连续两次的随访记录进行整合，并根据指南[1]中影响未来血压变化的相关因素确定模型输入，结果如表1所示。

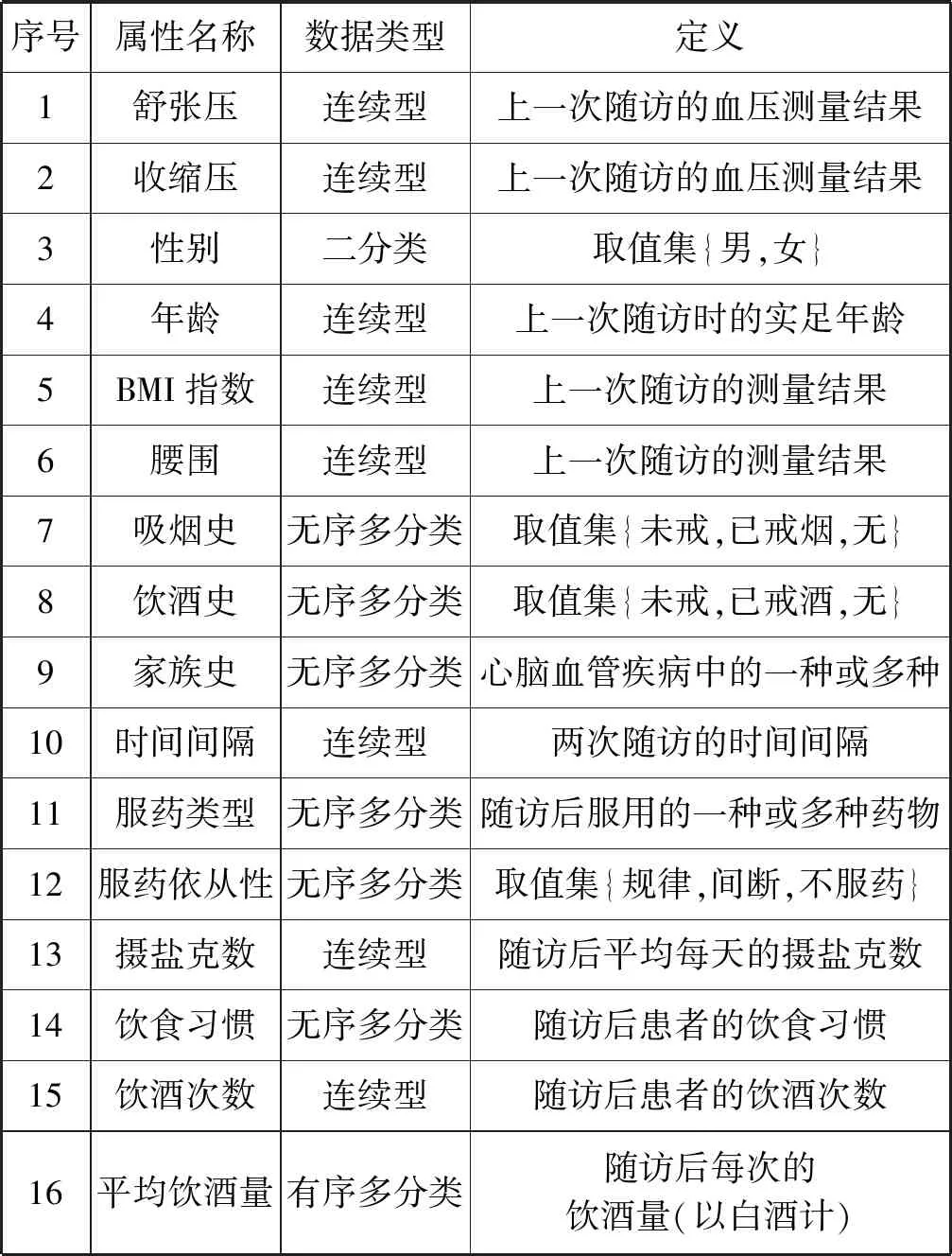
表1 血压预测模型输入特征定义表

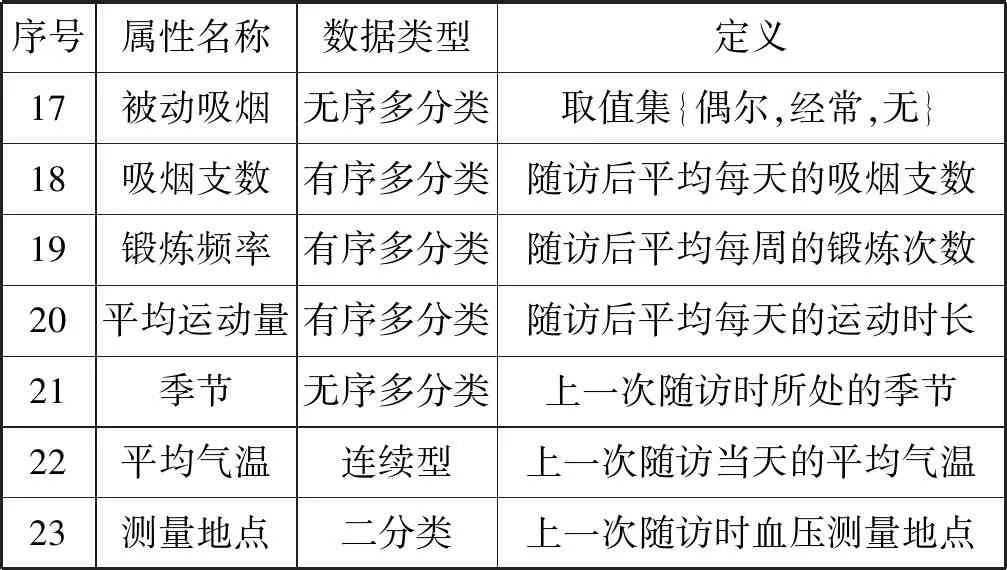
续表1

对于实验数据中不同类型的属性特征，本文采用不同方式进行处理。对于连续型特征，本文采用Z-score[16]完成归一化；对于二分类型特征，本文将两种类别分别映射为0和1；对于无序多分类型特征，本文先将其转换为多个二分类型特征，再分别对其编码，以季节特征为例，用是否为冬天、是否为夏天、是否为秋天、是否为春天表示原特征，1对应是，0对应否；对于有序多分类型特征，本文根据其取值集依次将其映射至[0,1]区间，以锻炼频率为例，将其取值集{从不,每周3次以内,每周3～6次,每天}分别映射为{0,0.333,0.667,1}。

实验硬件环境为i7处理器3.60 GHz，32 GB内存，GeForce 1080Ti独立显卡;软件环境为Windows 10操作系统，PyCharm集成开发环境，TensorFlow 1.4开源框架及Python 3.6。

3.2 性能评价指标

为了能更好地分析人体血压预测模型的准确度，使用绝对平均误差(Mean Absolute Error，MAE)和相对平均误差(Mean Relative Error，MRE)作为模型的性能评价指标，定义如下:

(12)

(13)

式中：youtput,i和yfact,i分别表示第i个样本血压的预测值与真实值。MRE与MAE的值越小，表示人体血压预测模型预测效果越准确。

3.3 参数设置与选择

由于本文所构建的人体血压预测模型采用深层RDBN网络结构，其隐藏层层数和每层中神经元个数会影响最终的预测效果及运算时间。因此，着重对这两个参数的选择过程进行分析。其他参数的设置参考文献[10-11,14]。

本文采用枚举法与重构误差法[15]相结合的方式确定隐藏层数目及每层神经元个数。首先，设置重构误差阈值，若当前GG-RBM单元的重构误差小于该阈值，那么就停止网络深度的累加；然后，枚举出顶层单元隐藏层神经元个数的可能值，选择使其可见层重构误差最小的神经元个数；再将顶层单元的隐藏层作为下一个单元的可见层，以同样方式确定下一个隐藏层的神经元个数；以此类推，直至根据阈值判断网络深度停止累加，从而获得最优网络结构。

实验设置如下：在样本数据集中随机抽取5 000个样本用于无监督训练，1 000个样本用于有监督微调，剩余1 000个样本用于测试。根据人体血压预测模型输入向量维数和实验设备的性能，重构误差阈值设置为5×10-4；隐藏层神经元个数取值范围设置为[10,60]，取值间隔为10。表2中给出不同网络结构下人体血压预测模型的表现，各指标均为重复实验10次后得到的平均值,其中粗体表示最佳结果。

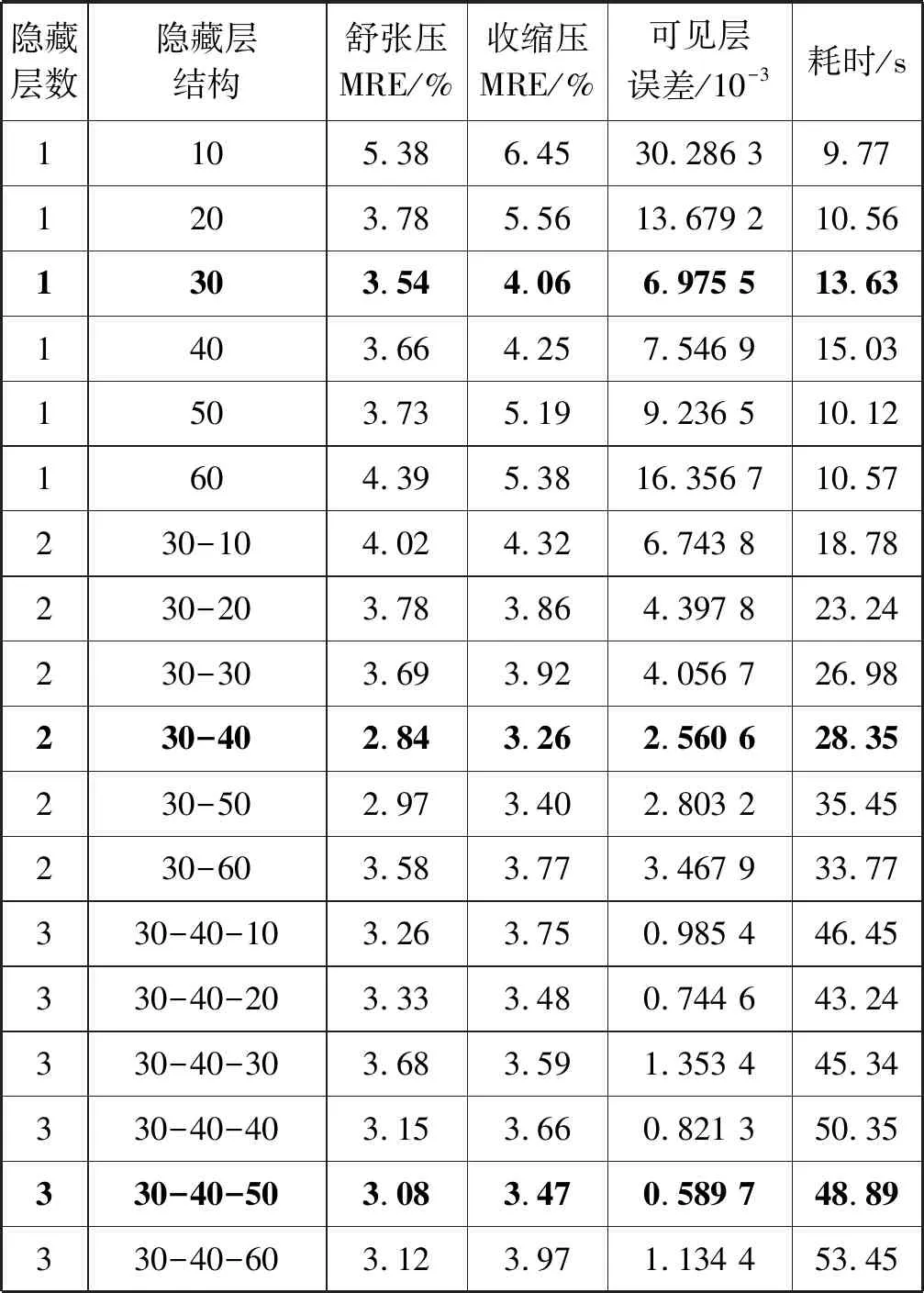
表2 不同网络结构的实验结果

可以看出，随着网络深度的不断增加，GG-RBM单元的可见层重构误差在不断减少，这是因为深层单元学习了低层单元对数据分布的先验知识，提高了重构信息的准确度；当隐藏层层数为2，神经元个数分别为30、40时，人体血压预测模型对于舒张压、收缩压预测的相对平均误差均达到最小，当网络继续加深时，误差反而变大。因此，基于RDBN的人体血压预测模型网络结构确定为4层，两个隐藏层的神经元个数从输入层向输出层方向依次为30和40。

3.4 不同模型对比分析

为进一步验证本文提出的基于RDBN人体血压预测模型的科学性与有效性，分别构建以下三种模型作为对比：传统 BP神经网络模型，定义为BP；顶层采用高斯-伯努利单元，其余各层采用BB-RBM的深层网络，梯度下降过程采用基于优化步长因子的Adam算法，定义为DBN-Adam；由GG-RBM单元组成的深层网络，梯度下降过程采用GD算法，定义为RDBN-GD。将样本数据集以6∶1的比例分为训练集和测试集，表3给出执行10次实验不同模型的性能指标。

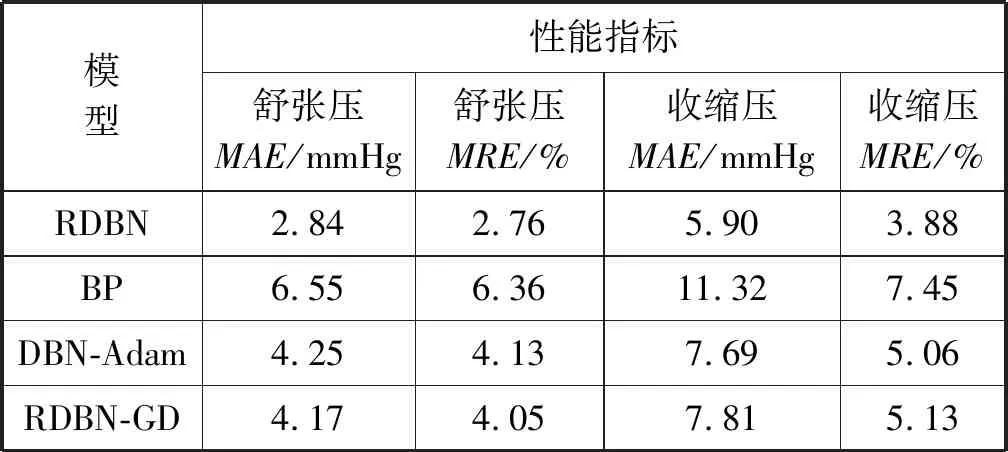
表3 不同模型性能指标对比

可以看出，本文提出的RDBN模型在挖掘多因素与患者未来血压值的复杂关系上表现优异，无论是舒张压预测还是收缩压预测，均比其他三种模型误差小，具有较好的预测精度。

同时，考虑到模型应用于实际血压预测的过程中必然需经过海量数据训练，遵循控制变量唯一的原则，比较RDBN模型与RDBN-GD模型随着训练集迭代次数的增加损失函数的变化情况，结果如图4所示。可以看出，本文提出的基于优化步长因子的Adam算法进行参数寻优的RDBN网络收敛速度较快，经过30次迭代后已接近最优解，能够大幅度节约建模的时间成本，而采用GD算法的RDBN-GD网络则需经过更多轮数的迭代。

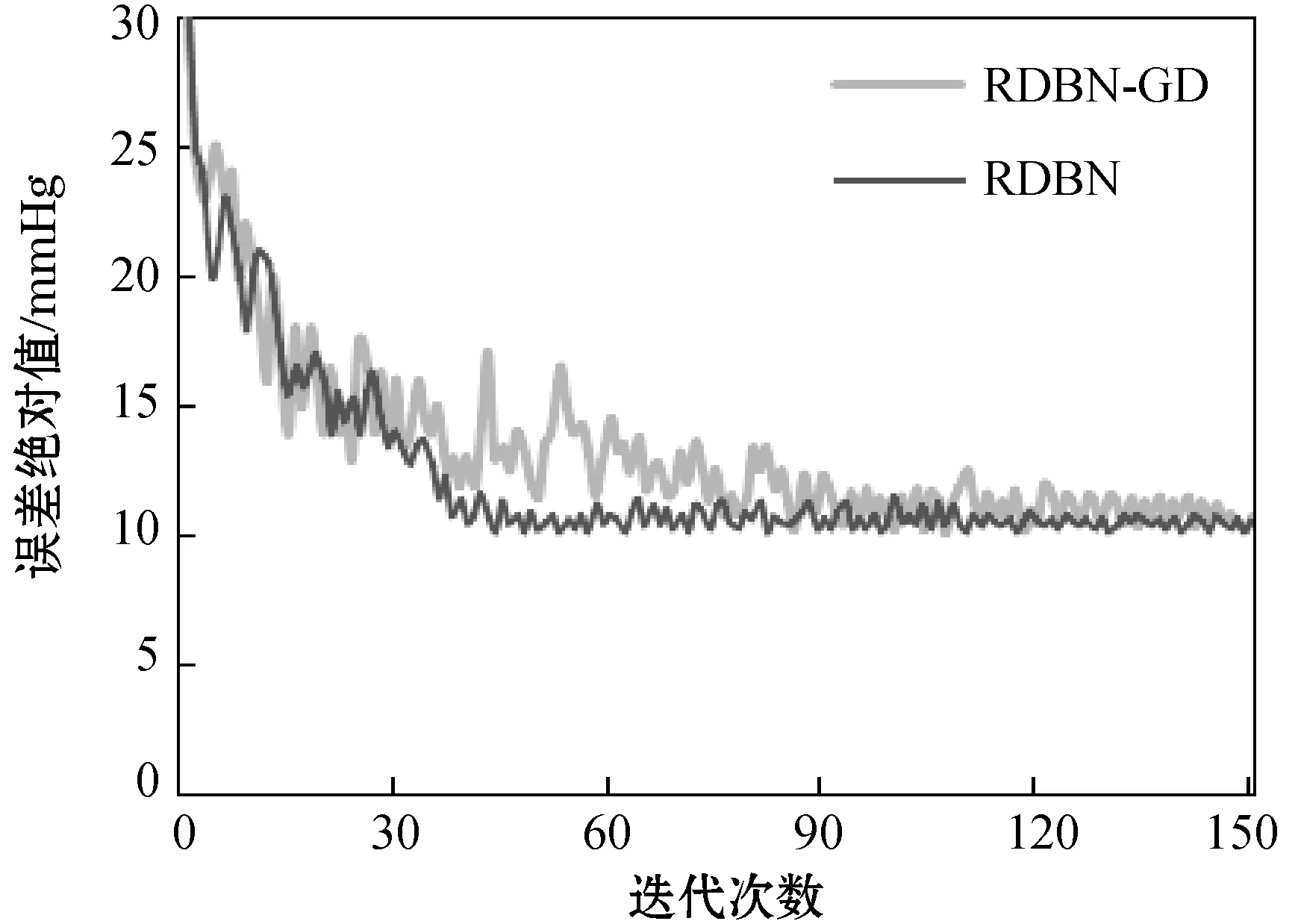
图4 训练误差迭代对比图

在不同模型性能对比的过程中，考虑到样本数据集中医生根据患者情况为其制定不同的随访周期，长期采取降压措施可能会影响患者的血压情况发生根本性改变，影响网络模型对数据的拟合，故按随访周期长短将样本数据集分为三类：周期在两周以内的、周期为两周至一个月的、周期在一个月以上的。图5和图6分别为四种模型在不同随访周期下对于患者舒张压、收缩压预测的平均绝对误差对比图。可以看出，随着预测时间跨度的增加，四种模型的预测精度均有所下降，但RDBN 模型相比其他模型更加稳定，符合患者对于采取降压措施一个随访周期后预测血压变化的需求。

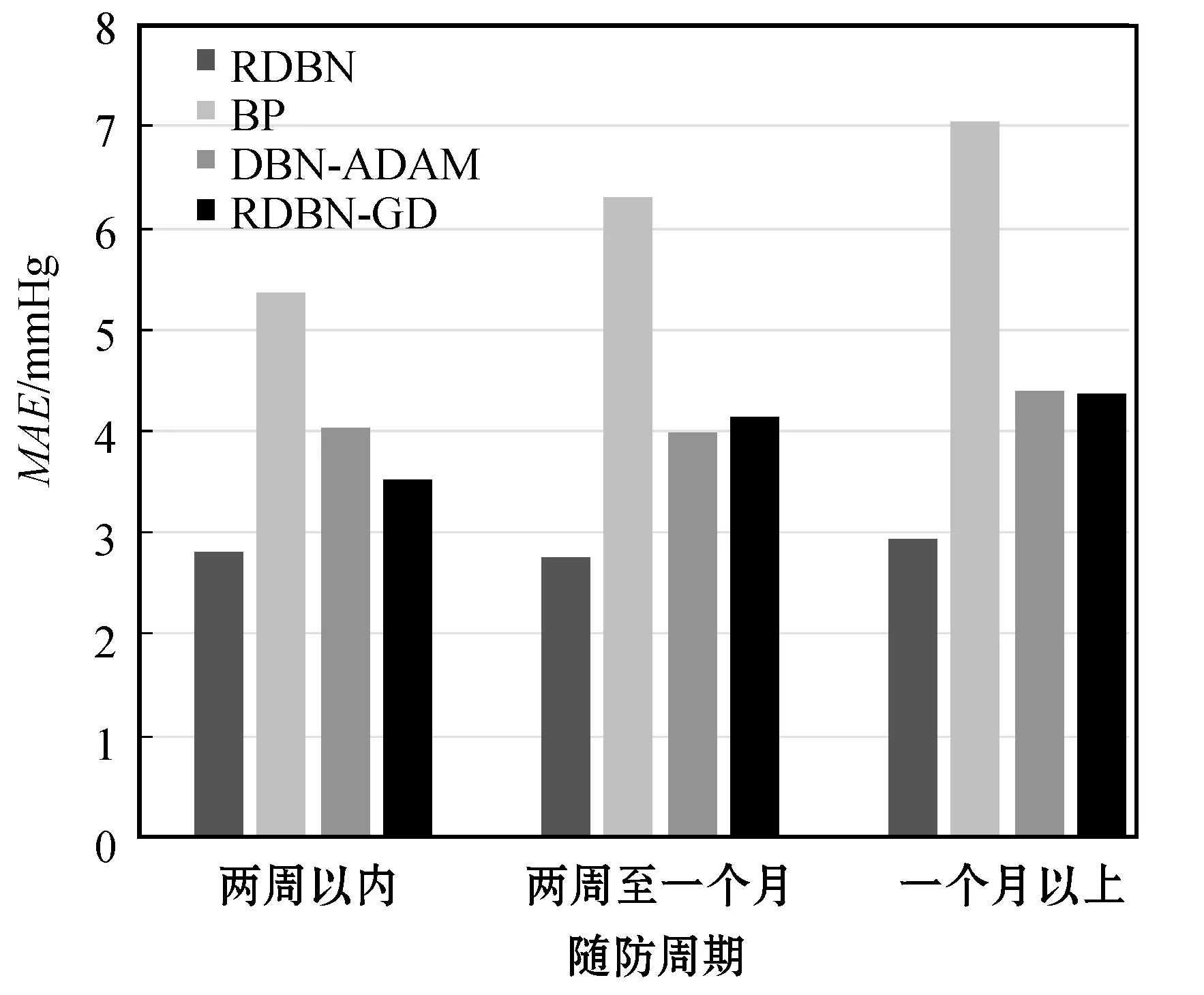
图5 不同模型舒张压预测绝对误差对比图

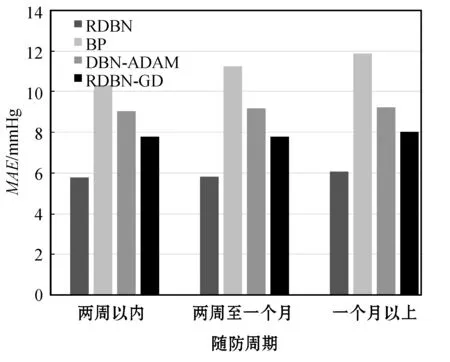
图6 不同模型收缩压预测绝对误差对比图

上述实验结果表明，本文提出的RDBN模型相较于其他网络结构，具有较优的训练效率与预测精度，能够表征人体未来血压情况与其多方面影响因素之间复杂的非线性关系，适用于医师为患者开具个性化降压策略的科学依据。

4 结 语

本文将实值深度置信网络应用于复杂环境下的人体血压预测问题中，根据患者的生理指标特征、所处环境因素特征、血压历史数据特征、采取的降压措施等多方面信息预测其未来血压状况。针对传统RBM只能接受二值型输入返回二值输出无法处理连续性数据的问题，提出能够接受实值输入返回实值输出的GG-RBM单元，以及采用了基于优化步长因子的Adam算法进行网络的有监督学习，加速了网络参数的寻优过程。通过实验证明本文提出的RDBN人体血压预测模型得到的预测值与实际值吻合程度较好，是一种科学有效的血压预测方法。在下一步工作中，期望能进一步完善模型，在定量分析相关因素对患者未来血压影响作用的同时，能够给出个性化的降压策略，实现对于高血压患者的精准医疗。