湍流边界层激励下平板振动响应相似性研究
2022-01-27赵国亮陈美霞
赵国亮, 陈美霞
(华中科技大学 船舶与海洋工程学院, 武汉 430074)
当潜艇在水下航行时,在其外壁会产生湍流边界层,因边界层内流体质点的运动速度是随机存在的,故在湍流边界层内部会产生非定常的随机脉动压力,这种随机的湍流脉动压力激励结构会使外壁产生振动并向外辐射噪声,也被称为“流激振动”或“流激响应”,它是水下结构水动力噪声的重要组成部分。
对于水下结构的流激噪声问题,因湍流脉动压力是随机产生的,理论分析比较困难,缩比模型试验成为研究流激噪声的重要技术途径。因此,必然会遇到模型与原型之间振动响应的相似关系问题。
若将湍流边界层的脉动压力作为随机信号,水下结构流激振动问题便可归于传统的随机声学问题。Hwang等[1]对1960年—2004年间的各种湍流边界层壁面压力谱模型的发展进行了综述,并使用这些模型与各种试验场景下测得的数据进行了对比,初步讨论了壁面压力谱的相似换算,其中Goody[2]提出的压力谱半经验模型能够在较宽的频带内提供较好的频谱预测,但未明确归一化方法在不同介质的壁面压力谱间的适用性。
壁面压力谱也被应用于流激结构振动响应领域的研究, Rosa等[3]采用Corcos[4]模型作为输入,采用模态叠加法计算了铝板一侧受湍流壁面脉动压力激励的结构振动响应,与数值仿真计算结果吻合较好。 Franco等[5]则对湍流边界层激励下平板响应的相似性定律进行了研究,对不同尺寸、材料平板进行了计算,并用理论、数值、试验的方法进行了验证,但并未考虑流体负载的情况。
由于水下结构物的流体负载影响不可忽略,为了明确湍流边界层激励下平板在不同流体介质中振动响应的相似性换算关系,以指导其在工程实际中的应用,本文在上述研究的基础上首先验证了脉动压力谱归一化方法在不同介质间的适用性,其次对考虑流固耦合的流激结构响应间的相似换算关系进行了假设和验证,并给出了具体的公式以量化分析,为同种以及不同介质流激结构缩比模型的设计及响应预报提供一定的参考。
1 理论分析
对于随机声学问题,因湍流脉动压力激励作用具有随机性,各激励力之间存在时空相关性,故随机振动的研究更复杂。
根据随机理论[6],湍流激励下弹性结构振动位移响应的互功率谱密度表达式如下
Sw(x,ξ,ω)=∬Spp(ξ′,ω)Hw(x,x′,-ω)·
Hw(x+ξ,x′+ξ′,-ω)dx′dξ′
(1)
式中:x=[x,y]为观测点坐标;ξ=[ξx,ξy]代表两个观测点之间的空间距离向量;ω为圆频率;Spp(ξ′,ω)为壁面脉动压力互功率谱密度;Hw(x,x′,-ω)为结构振动位移的单频响应函数。
位移单频响应函数的物理含义为:弹性结构上的点x在位于x′处以圆频率为ω的单位简谐力作用下的振动位移响应。
式(1)表明:求解振动位移响应的关键在于得到湍流脉动压力的互功率谱密度以及场点振动位移的单频响应函数。
1.1 平板湍流脉动压力互功率谱密度
Corcos建立了经典的湍流脉动压力模型,湍流边界层的脉动压力在空间域上的互功率谱密度如下所示
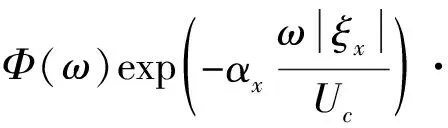
(2)
针对水中低马赫数运动的结构物,Hwang等指出:Corcos模型往往高估湍流边界层壁面脉动压力功率谱在低波数区的谱级,并提到一种改进型Corocs模型弥补了原型的不足。因此下文采用改进型Corcos模型
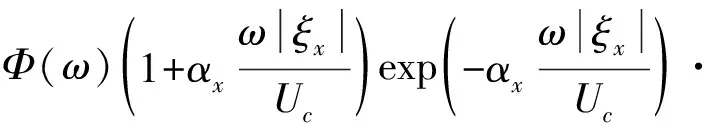
(3)
式中:Φ(ω)为平板湍流脉动压力自功率谱密度,其选择见1.2节;ξ为激励两点空间距离的向量;ξx,ξy分别为两点的流向和展向间距, 其中ξx=x2-x1,ξy=y2-y1,流向与展向相干函数衰减因子分别取αx=0.116,αy=0.7;i为虚数单位;U∞为远方来流速度;Uc为边界层在来流方向的迁移速度,Uc=βcU∞,βc根据试验取0.6~0.8,本文取0.65。
1.2 脉动压力自功率谱密度
Hwang等将湍流边界层研究以来发展的壁面压力谱的半经验模型与试验结果进行对比,其中Goody模型描述的壁面湍流脉动压力自功率谱密度模型在风洞、水洞等实验场地的预报结果在各频段对比良好。
对于壁面上的二维、零压力梯度流,Goody给出壁面脉动压力的自功率谱密度如下所示
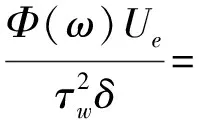
(4)
式中:Ue为壁面边界层外缘速度,对于平板模型可近似取Ue=U∞;τw为壁面剪切应力;δ为边界层厚度;RT=(δ/Ue)/(υ/uτ);υ为流体运动黏度;uτ为壁面摩擦速度。
1.3 湍流激励简支平板的单频响应函数
考虑一充分发展的湍流作用在长宽分别为a、b的四边简支薄板上,薄板浸没在密度为ρ0,声速为c0的流体中,平板z>0的表面受到来流速度为U∞的湍流脉动压力的激励。如图1所示,本文考虑远场流速U∞与声速c0相比可以忽略不计,因此不考虑对流运动对声速的影响,可以认为声速为一恒值。
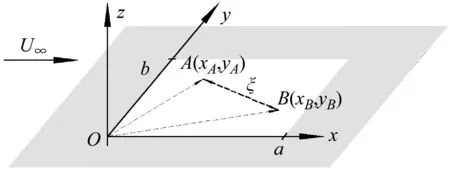
图1 无限大刚性挡板上四边简支平板及坐标参考系Fig.1 Four-sided simply supported flat plate and coordinate reference system on infinite rigid baffle
用Corcos模型描述的脉动压力功率谱作为输入,将其视作一种外力激励平板,流场-平板耦合振动的控制方程可写成
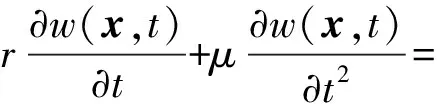
p(x,t)+pa(x,0+,t)-pa(x,0-,t)
(5)
式中:w(x,t)为简支板的振动位移函数;D为平板的弯曲刚度,D=Eh3/12(1-υ2);υ为泊松比;r为损耗因子;μ为平板的面密度;t为时间;p(x,t)为湍流边界层的脉动压力;pa(x,0+,t)为平板z>0表面的声压;pa(x,0-,t)为平板z<0表面的声压。结构振动位移的单频响应函数与简支板的振动位移函数之间满足以下关系
Hw(x,x′,-ω)eiωt=w(x,t)
(6)
湍流边界层脉动压力p(x,t)表达式如下
p(x,t)=δ(x-x′)eiωt
(7)
平板振动引起的声压满Helmholtz波动方程
(8)
平板与流场耦合的连续性条件如下所示
(9)
根据文献[7],流体负载平板的振动位移函数w可表示如下
(10)
式中:Wmn(ω)为模态参与系数;αmn(x)为简支板在真空中归一化的固有振型函数。在(0,0)≤x≤(a,b)的空间域中,其表达式为
(11)
固有振型函数αmn(x)对应的本征频率如下
(12)
定义傅里叶变换对
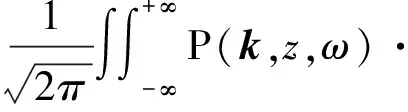
exp[i(k·x+ωt)]dkdω
(13)
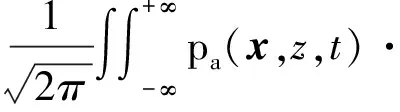
exp[-i(k·x+ωt)]dxdt
(14)
式中:k=[kx,ky],由式(6)及声场辐射条件得
(15)
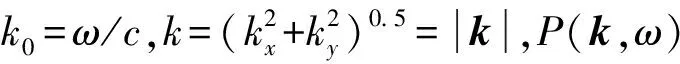
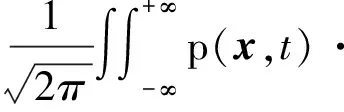
exp[-i(k·x+ωt)]dxdt
(16)
根据以上公式,由附录A的推导,可得平板振动位移的单频响应函数Hw的表达式为
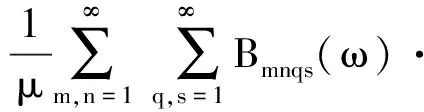
αmn(x)αqs(x′)
(17)
平板上某一点(x,y)的速度可以表示为v(x,t)=∂w(x,t)/∂t,结合式(1)、式(6)可得平板振动位移与振动速度互功率谱间的关系如下
Sv(x,ξ,ω)=ω2Sw(x,ξ,ω)
(18)
结合式(1)、式(3)和式(18),可得平板振动速度的互功率谱密度
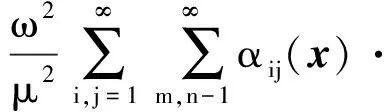
∬Spp(ξ′,ω)αkl(x′)·α(x′+ξ′)dx′dξ′
(19)
通过将式(19)中的ξ设为0,可以得到平板给定节点的振动速度自功率谱密度函数,如下所示
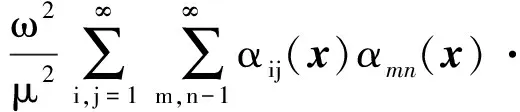
αkl(x)·α(x+ξ)dxdξ
(20)
平板振动的平均速度响应可用如下面积平均来表示,根据模态振型的正交性,积分可以简化如下
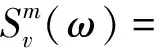
(21)
式中:Zmmnn(ω)为阻抗,其表达式如下
Zmmnn(ω)=μCmnmn(ω)
(22)
其中N和M为模态截断数,式(21)中的受纳函数Amnmn(ω),其积分形式如下所示
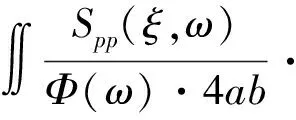
αmn(x)αmn(x+ξ)dxdξ
(23)
式(23)中的积分,可采用文献[8]中的方法并结合数值积分计算。得到流激平板结构振动响应的表达式,接下来考虑其存在的相似关系。
1.4 不同流场介质平板响应相似性准则
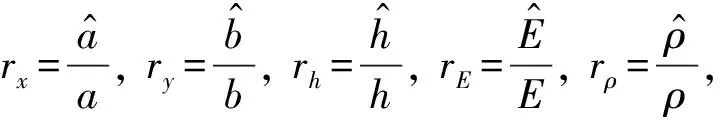
(24)
对于本文所研究的流激响应问题,若原始模型与相似模型外流场的雷诺数Re较大的时候,流动进入紊流粗糙区,此时流动的阻力大小与Re无关,只与相对粗糙度有关,这个流动范围称为自模区。若原型与模型的两个流动都处于自模区,则只做到几何相似,而不必Re相等,就自动实现了动力相似。本文研究的流动均处于自模区。
忽略湍流边界层时均压力对平板变形量的影响。采用模态叠加法计算湍流边界层激励下平板响应,真空中平板振动平均速度的一种相似性准则在文献[10]的基础上出
(25)
其中,第一条假设约束了相似平板的长宽几何相似,第二条假设约束了相似平板的计算频段的缩比因子需要与振型的本征频率的缩比因子保持一致,第三条假设在前两条假设的基础上给出了远场流速如何设计,其中cs为一常数。
本文考虑流体负载的计算方法,同样采用模态叠加法。为观察这套相似性准则是否依然适用,考虑累加项中的受纳函数Amnmn(ω),将式(24)及式(25)代入式(23),当计算频率较高时,可得受纳函数的缩比因子如下所示
(26)
再考虑累加项中阻抗项Zmmnn(ω),结合式(22)与式(25),得到阻抗缩比关系见附录B。
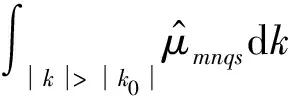
两个积分项的展开如附录C所示:根据附加质量项与附加惯性项显示的被积函数和积分上下限的特征,引入第四条假设
(27)
第四条假设引入了湍流介质的声速,根据式(25)中的第三条假设,实际上约束了流场声速与流速的缩比因子必须相等。将假设(27)代入到式(22)的积分项中,同时结合简化后阻抗的缩比关系的特征,引入第五条假设
(28)
第五条假设引入了湍流介质的密度,表明湍流介质与平板长宽尺度的缩比因子之积必须与平板面密度缩比因子相等。将式(27)与式(28)的假设代入式(22),阻抗缩比关系可简化为下式
(29)
(30)
式(30)实际上约束了在外流场给定情况下,平板材料必须满足的条件。结合式(25)、(26)、(29),可以得到用湍流脉动压力自功率谱密度函数归一化的平板弯曲振动位移平均速度响应间的缩比关系
(31)
对式(31),要得到平板弯曲振动位移平均速度响应的缩比关系,需要考虑脉动压力自功率谱的相似性。
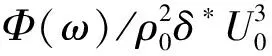
将脉动压力自功率谱密度按Hwang所给方法归一化处理之后得到平板弯曲振动位移平均速度响应间的缩比关系
(32)
需要注意的是,这些相似性准则的推导是在假定Corcos模型中的系数αx,αy不随频率改变的前提下进行的,在对相似平板通过相似性准则得到缩比的湍流流速之后,平板的计算频率和响应需要依据公式进行缩比。
本文推导相似换算方法,是在以下五条假设的基础上建立的
(33)
对于各向同性的相似平板和原型平板,如果它们均为四边简支边界条件,相似换算的整个流程可总结如下:
(1) 若平板的长宽几何相似,则两个平板间就具备了相似的前提。在选定外流场的前提下,根据式(30)可得相似平板的材料应满足的特征,确定好相似平板的材料后,根据假设5设计相似平板的长宽与厚度。
(3) 最后计算缩比模型振动速度响应的缩放因子,对相似平板的计算频率和响应分别按照式(25)与(32)进行缩放,即可实现对原型平板响应的预报。
综上,考虑流体负载的情况下,可通过对尺寸、材料属性、流速等的配合,可以实现不同流体介质下模型响应间的相似换算。
2 算例验证与分析
针对1.4节提出的不同流体介质中壁面湍流脉动压力自功率谱密度归一化与四边简支板流激响应的相似准则问题,用以下算例进行了验证。
2.1 流激响应相似性准则验证
为了验证并说明1.4节提出的相似性换算关系的适用范围,选取几种具有典型缩比关系的平板,它们各自的尺寸和相应的缩比因子如表1所示。其中平板P0被选作原型平板,其材料为钢,钢材参数如表2所示,外流场为水;P1为长宽厚等比例缩放的钢板,外流场为水;P2代表厚度与长宽缩比因子不等的平板,外流场同样为水,以上三种方案的湍流边界层在流经平板前缘之前经过长为1 m,表面粗糙度为0.000 2的区域;P3代表厚度与长宽缩比因子不等的平板,外流场为空气,流场流经平板前缘之前经过长为1 m,表面粗糙度为0.002的区域。其中P2~P3模型的密度和弹性模量暂不考虑实际情况,以上四种方案均认为湍流边界层在平板上的脉动压力与湍流在平板前粗糙区域充分发展后的脉动压力保持一致。经检验以上流动均已进入自模区[16]。

表1 平板P0~P3的参数与相应的缩比因子
理论分析部分假定平板均为四边简支的边界条件,对于原型平板,假定远方来流速度为10 m/s,计算中取横、纵半波波数均为15,在计算频段范围,这个横、纵半波波数经过了模态收敛性验证,结构响应可计算到1 500 Hz,剩余平板采用了同样的半波数组合,并假定泊松比和结构阻尼不随频率改变。表2给出了P0~P3平板的参数与缩比因子。
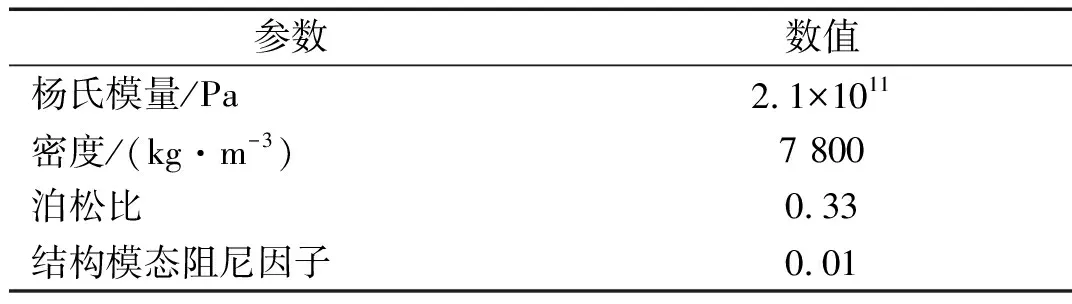
表2 钢材材料参数
平板区域内以边界层厚度以及壁面剪切应力均以平板前缘为准,可以验证以上流激响应方案均已进入紊流粗糙区。根据文献[17],各方案紊流粗糙区边界层时均参数如表3所示。
首先对脉动压力自功率谱密度的归一化方法进行验证,根据表2所给参数,以ω为横坐标,脉动压力自功率谱为纵坐标,对比四种方案下的湍流脉动压力自功率谱特性,如图2所示。
运用1.4节描述的中、低频段脉动压力归一化处理方法,得到缩放后的脉动压力自功率谱密度对比如图3所示。
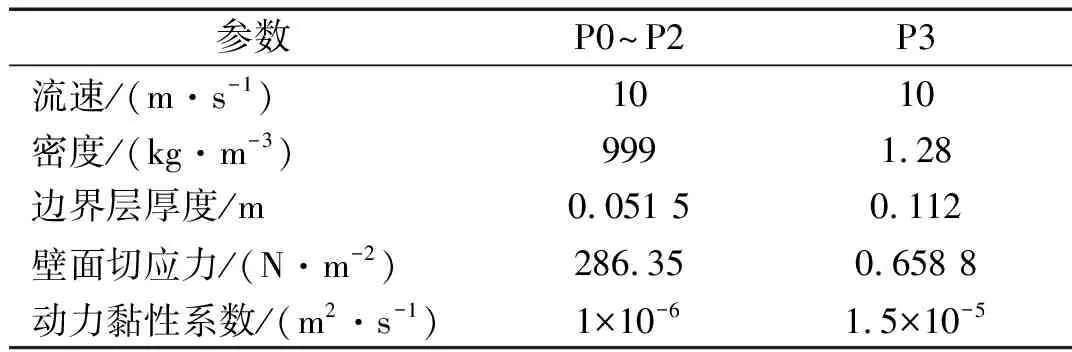
表3 边界层时均参数计算结果
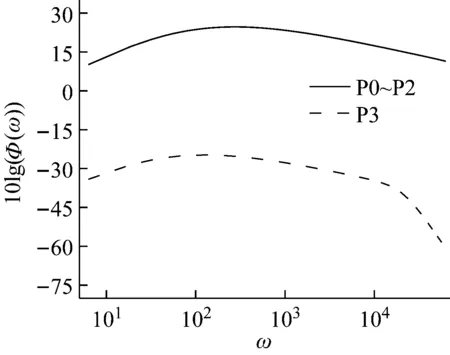
图2 脉动压力自功率谱密度(未缩放)Fig.2 Pulsating pressure self-power spectral density (unscaled)
经检验,本文算例的脉动压力自功率谱密度函数在所属频段应用该缩放尺度可以实现归一化。
依据表1所给参数中的长宽、厚度、材料属性、流速等作为输入,对尺寸、材料、外流场均变化的平板P0~P3的响应分别进行计算,横坐标的计算频率保持0~1 500 Hz,所得振动速度响应对比如图4所示。
原型平板的计算频率和响应保持不变,对相似平板的计算频率和响应分别按照式(33)与(32)进行缩放。得到缩放后振动速度响应对比如图5所示。
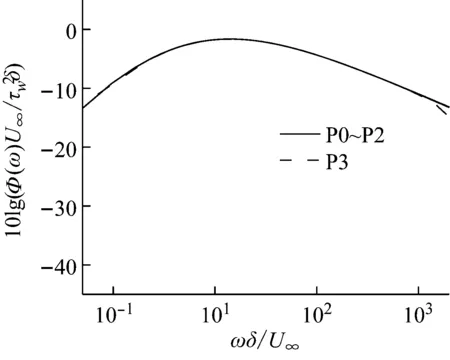
图3 脉动压力自功率谱密度(用中、低频的缩放尺度)
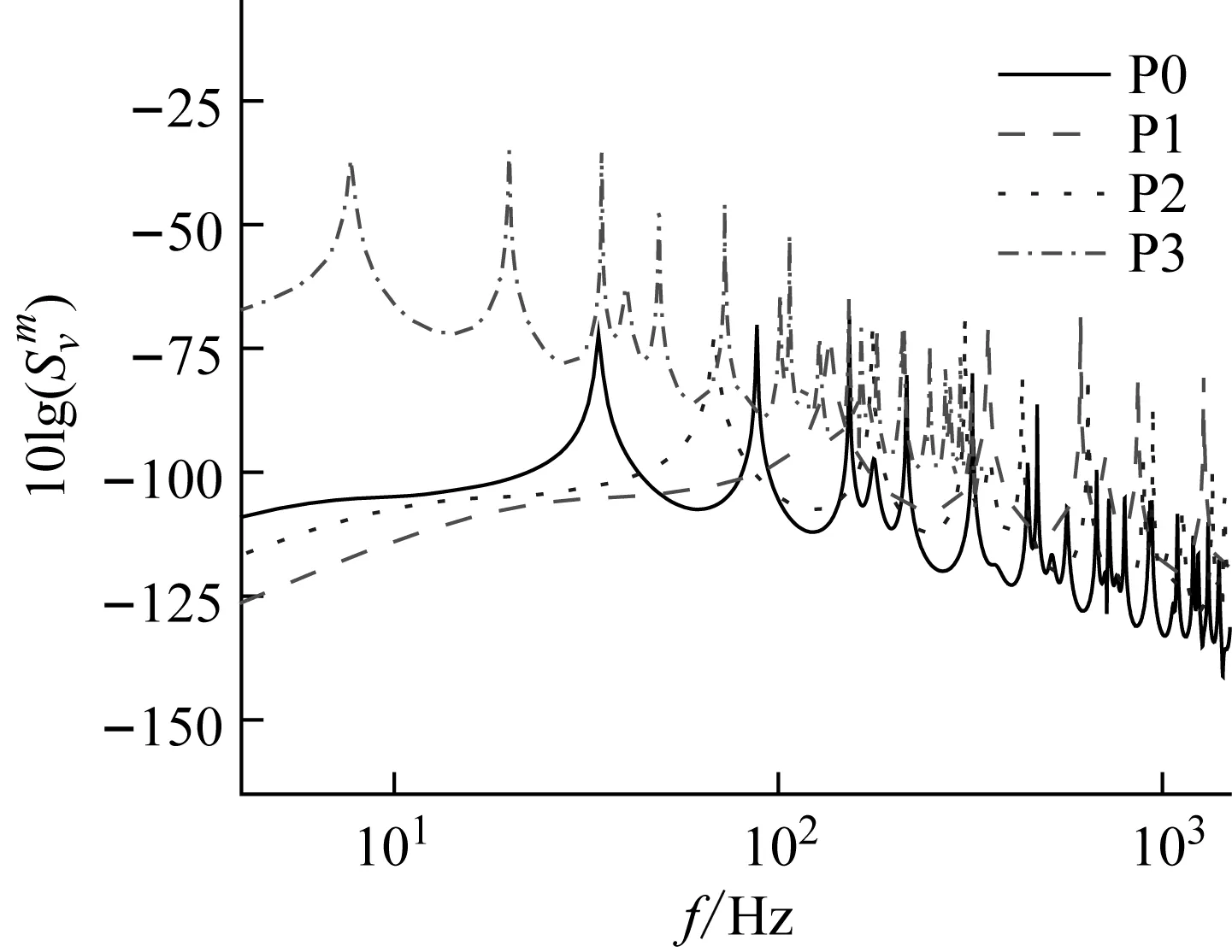
图4 平板平均振动速度(P0~P3未缩比)
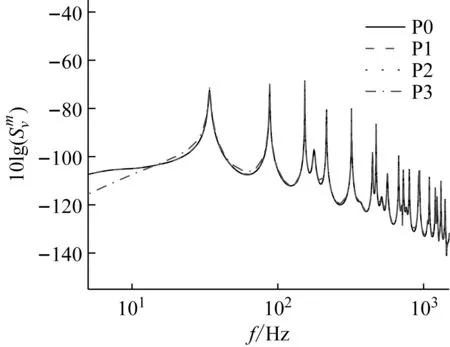
图5 平板平均振动速度(P0~P3缩比换算后)
通过图4、图5的对比可知:尺寸不同、材料不同、外流场不同的平板速度响应一般各不相同。但这些平板的响应经过尺寸设计和相似换算,可以得到与原型平板的响应结果的重合。
3 结 论
本文结合改进的Corcos模型描述的脉动压力激励下平板振动速度响应的特点,将平板振动响应的互功率谱密度分解为湍流脉动压力互功率谱密度函数和结构振动位移的单频响应函数。
对于壁面湍流脉动压力自功率谱密度,验证了脉动压力归一化的方法在不同流体介质间的适用性。对于结构振动位移的单频响应函数,考虑其相似性提出了五个假设,在此基础上推导了相似换算方法,给出了速度响应换算的具体公式。最后对几类平板弯曲振动的平均速度响应进行了计算与换算,通过对比,得到了以下结论:
(1) 湍流壁面脉动压力自功率谱密度的归一化方法,在不同流体介质间有适用性。
(2) 同种介质湍流脉动压力激励下,材料相同,几何等比例缩放的平板,可以通过流速和频段的设计,依据本文的方法实现相似换算。
(3) 同种介质湍流脉动压力激励,几何不全相似的平板,以及不同介质湍流脉动压力激励下的平板,其振动响应在理论上可以依据本文方法实现相似换算。但模型材料受外流场密度与平板面密度的限制,工程实现难度大。该理论在不同外流场介质中的应用可为之后的研究提供一定的参考。
本文中Corcos模型激励下平板响应的换算是在泊松比、结构阻尼、Corcos模型参数等不随频率变化的前提下完成的,对于试验 的复杂情况,应作专门的研究,对相似性准则进行修正。
附录A 平板振动位移的单频响应函数Hw推导
由式(9)、式(10)、式(13)、式(14)和式(15)可得声压的表达式为:
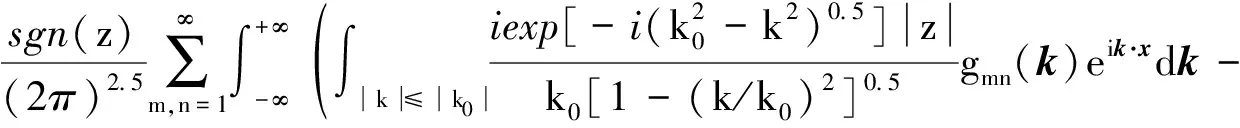
(A.1)
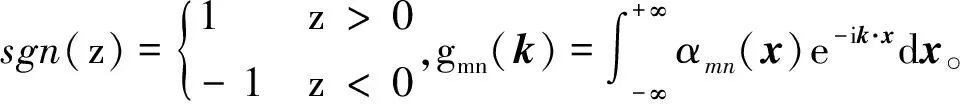
将式(10)、式(13)、式(15)代入到总控方程中,并对方程两边进行傅立叶变换和正交变换,可得耦合振动控制方程为:
(A.2)
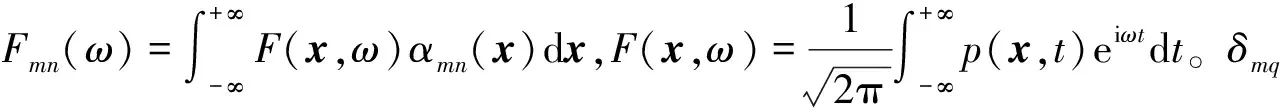
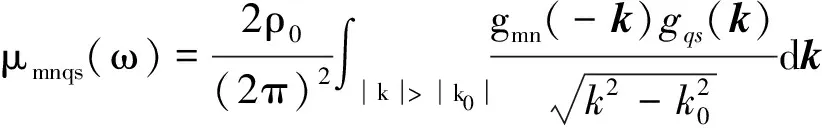
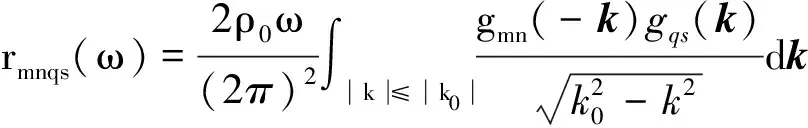
定义:
(A.3)
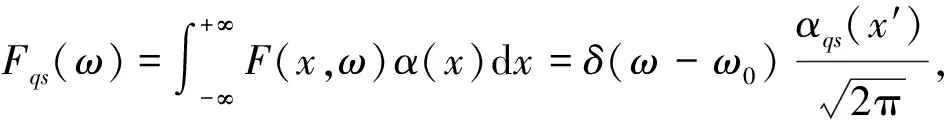
附录B 阻抗缩比因子
(B.1)
附录C 附加质量项与附加惯性项的积分展开
附加质量项积分展开:
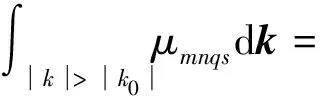
(C.1)
附加惯性项积分展开:
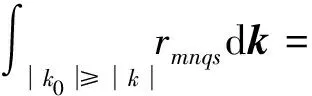
(C.2)
