光滑环形气体密封动态特性研究

杨兴辰， 张万福,2， 张晓斌， 陈璐琪， 顾承璟， 李 春,2

(1.上海理工大学 能源与动力工程学院，上海 200093； 2.上海市动力工程多相流动与传热重点实验室，上海 200093；3.华北电力科学研究院有限责任公司，北京 100045； 4.上海福伊特水电设备有限公司，上海 200240)

光滑环形气体密封广泛用于各类透平机械，以减小流体从高压区至低压区泄漏，其性能对机组工作效率具有重要影响[1-2]。同时，理论与实际表明密封内泄漏流体易产生使转子失稳的气流力，严重威胁机组的安全稳定运行，密封动态特性及其对系统稳定性的影响进行研究尤为重要[3-6]。

Lomakin[7]发现光滑环形气体密封具有直接刚度可以提高转子临界速度以来，有关密封动力特性的研究越来越深入。Alford[8]指出环形密封由于转子旋转产生切向气流力不利于系统稳定。考虑到密封气流力受转子所在位置影响，Allaire等[9]最先研究了高偏心对光滑环形气体密封的影响，充实了有关密封高偏心的理论研究。Nelson等[10]通过快速傅里叶变换对光滑环形气体密封进行研究，发现密封在高偏心下交叉刚度与交叉阻尼系数显著提高。Alexander等[11]通过试验发现随偏心率的增加，易产生负静态刚度系数。Arghir等[12]理论研究了不同转速下，转子刚度系数随偏心率的变化，表明由于小间隙处的黏性效应，影响了使转子恢复同心状态的气流力，造成负刚度。然而，上述研究均未考虑转子涡动对密封动力特性系数的影响。Kerr[13]通过试验研究涡动转子密封动力特性系数，发现密封气流力造成的负刚度是系统失稳的主要原因。

环形密封通常工作于阻塞或非阻塞状态，Fleming[14]研究发现光滑环形密封在阻塞工况下，易产生负刚度，而非阻塞工况则不会出现负刚度，为避免负刚度可串联多个密封降低级间压比。Arghir等[15-16]等分析了密封阻塞工况下的流场，表明负刚度系数是阻塞流动造成。然而，Childs等[17]通过试验发现，非阻塞工况也会产生负刚度。此外，环形密封内动力特性受密封结构影响，Childs[18]指出密封流动特性在一定程度上受长径比影响，从而改变密封动力特性。然而，对于不同流动状态、偏心率及长径比工况下光滑环形气体密封动态特性尚没有较为系统的研究。

本文应用计算流体力学方法研究了光滑环形气体密封流动特性，并基于微元轨迹理论方法[19]系统分析出口状态、偏心率及长径比对光滑环形气体密封动力特性系数影响。

1 数值计算方法

1.1 密封结构几何模型

本文采用Childs试验光滑环形气体密封模型尺寸[20](密封长度L=100 mm, 转子直径D=100 mm, 密封间隙Cr=0.305 mm)，并增加密封长度为50、150 mm的两种模型。表1为密封的几何参数，图1为试验密封几何尺寸。

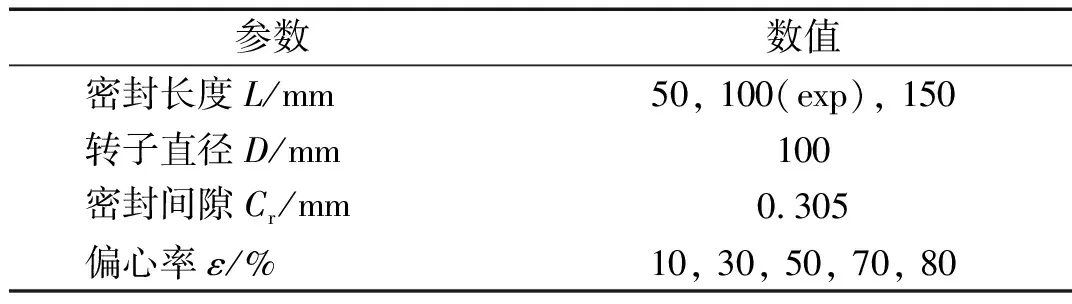
表1 光滑环形气体密封几何参数

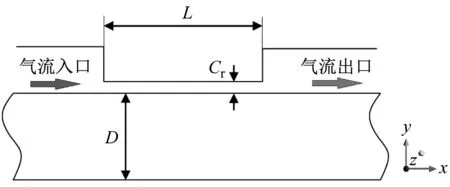
图1 光滑环形气体密封几何尺寸Fig.1 Geometric dimensions of the smooth annular gas seal

转子偏心率ε为

(1)

式中,e、Cr分别为转子y方向偏心距与半径间隙。

1.2 数值模型

采用结构化网格，建立光滑环形气体密封三维计算模型，并对模型(Pout=1.0、ε=50%、L/D=0.5)进行网格无关性验证，分别对网格量为156、188、204、224、246万进行计算分析，结果如图2所示，相同工况下密封气流力随网格数量增加而增大，当网格数量超过204万时，密封气流力无显著变化。综合考虑计算资源与精度，确定长径比(L/D=0.5)时网格数量为204万。经验证，各长径比密封(L/D=0.5, 1.0, 1.5)网格总数分别为204、546、555万。图3为光滑环形气体密封的网格分布情况。

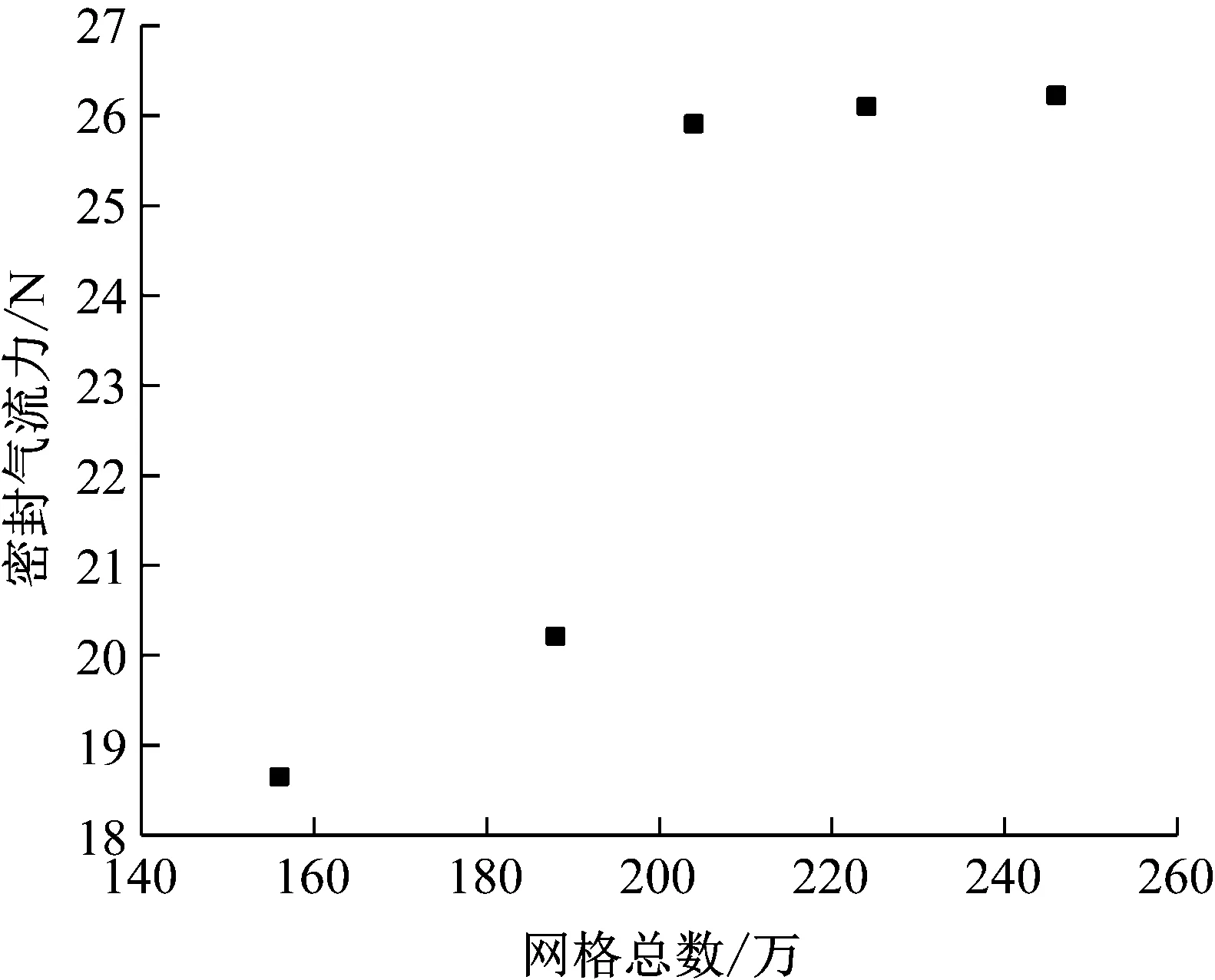
图2 网格无关性验证Fig.2 Grid verification

图3 计算网格分布Fig.3 Grid distribution

1.3 边界条件

对光滑环形气体密封动态特性进行研究，进口压力恒定，改变其出口压力使流体处于阻塞/非阻塞工况。针对不同密封结构及工况，调整瞬态计算所用的时间步长。采用动网格方法对密封模型进行计算模拟，运用CEL(CFX Expression Language)设定网格运动轨迹。表2为光滑环形密封的瞬态计算边界条件。

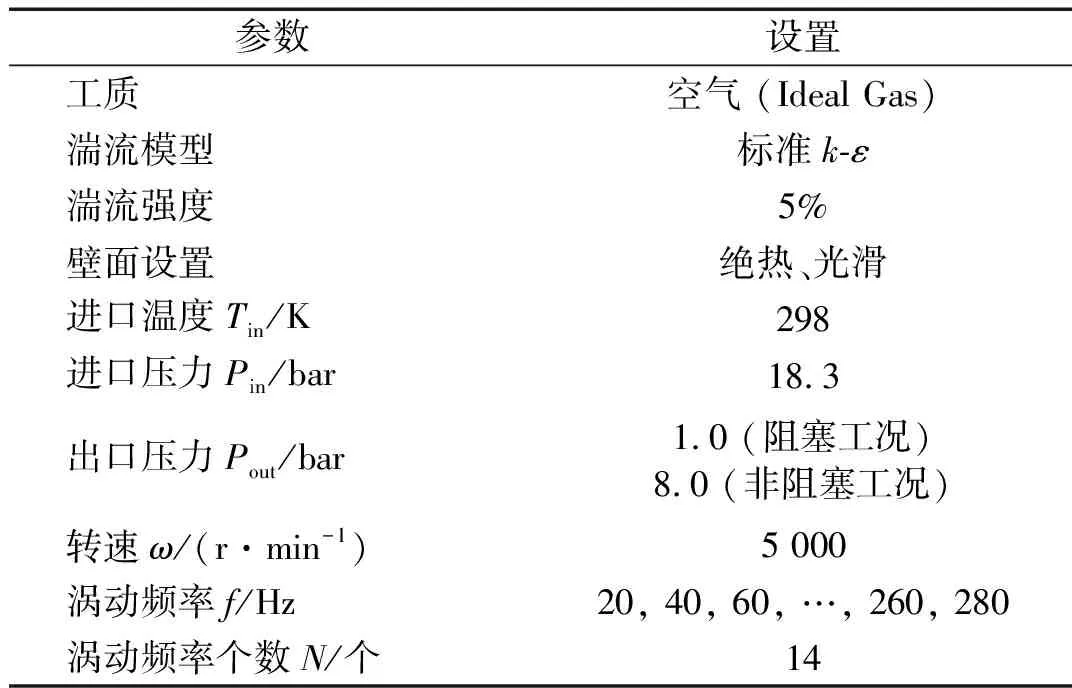
表2 工况参数

1.4 动力特性系数识别方法

基于微元理论方法识别密封动力特性系数，计算密封在2种出口状态(非阻塞/阻塞)、5种偏心率以及3种长径比工况下密封动力特性系数。

在理想状态下，密封系统转子与静子为同心状态，转子绕密封中心点O以角速度ω转动。但在实际运行工况中，转子中心C一般绕涡动中心O1以一定的角速度Ω涡动。图4给出了密封动力特性识别模型，假设该涡动轨迹为椭圆形。分别以O、O1为原点建立(X,Y)与(x,y)坐标系，以O1为旋转中心将(x,y)坐标系逆时针旋转至x轴与椭圆轨迹长轴重合，设此时旋转角度为θ，建立(e,α)坐标系。

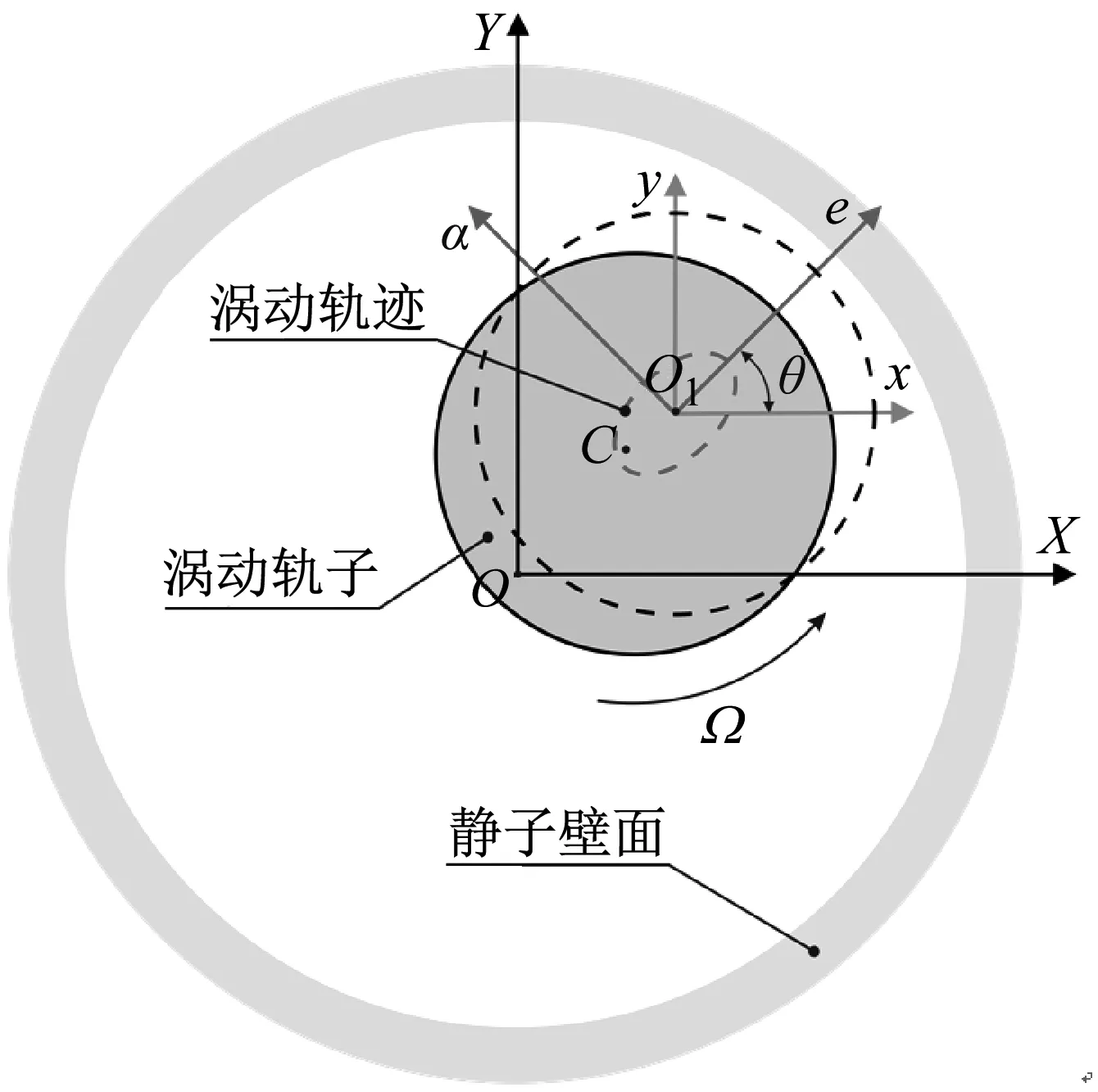
图4 密封动力特性识别模型Fig.4 Schematic model of the whirling orbit

令a、b为椭圆轨迹的长、短半轴长度，在(X,Y)坐标系下的椭圆轨迹方程为

(2)

在(e,α)坐标系下，涡动轨迹方程及相应涡动速度分别由式(2)、(3)所示

(3)

(4)

当涡动轨迹较小，密封动力特性模型可线性简化为

(5)

式中：ΔFe、ΔFα为转子所受气流力与静态气流力之差；Kee、Keα、Kαe、Kαα为密封刚度系数；Cee、Ceα、Cαe、Cαα为密封阻尼系数。

通过瞬态计算可得任意涡动转速下转子受力。现取t=0和t=T/4时刻，转子在e方向和α方向气流力之差分别为ΔFe(t=0,Ω=Ωi)、ΔFα(t=0,Ω=Ωi)、ΔFe(t=T/4,Ω=Ωi)、ΔFα(t=T/4,Ω=Ωi)，化简可得：

(6)

(7)

计算相应动力系数并转换其坐标可得密封的刚度与阻尼系数

(8)

(9)

为衡量密封对转子系统稳定性的影响，引入有效阻尼系数Ceff，有效阻尼系数越大，系统越稳定[21]。

(10)

2 计算结果与分析

2.1 模型验证

本文密封模型基于文献[20]试验尺寸，其静态刚度系数试验值为-1.93 MN/m。本文模拟密封气流力及静态刚度系数随偏心率的变化趋势，如图5所示。密封静态刚度系数约为-1～-2.6 MN/m，ε≈75%时，模拟值与试验值-1.93 MN/m吻合。

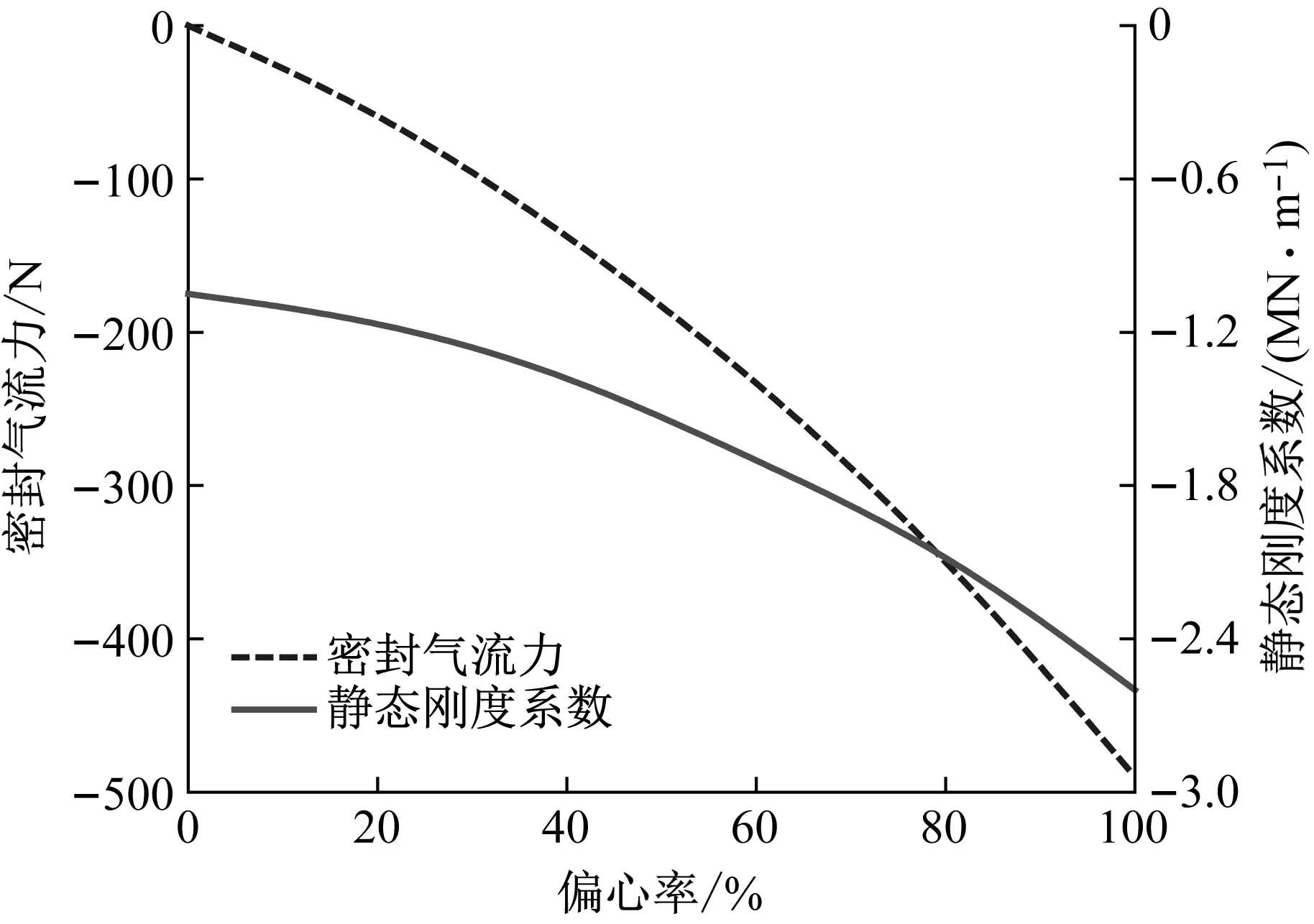
图5 密封气流力及静态刚度系数随偏心率变化Fig.5 Fluid-induced force and direct static stiffness vs. eccentric ratio

2.2 转子偏心对密封动力特性的影响

2.2.1 非阻塞状态密封流动特性

图6为非阻塞状态不同偏心工况下(L/D=1.0)，密封刚度系数随涡动频率的变化趋势。由图6(a)、(b)可知：① 随偏心率的增加，密封直接刚度系数逐渐降低；② 当ε>30%时，直接刚度系数Kxx≠Kyy，且Kyy30%时，交叉刚度系数(-)Kxy≠(+)Kyx，且Kxy的绝对值增量大于Kyx；③ 密封交叉刚度系数对涡动频率依赖性较低，涡动频率变化，密封交叉刚度系数变化几乎可以忽略不计。

图7给出了非阻塞状态不同偏心工况密封阻尼系数随涡动频率的变化趋势。由图7(a)、(b)可以看出：① 任意偏心工况密封直接阻尼系数均为正值，且其值随偏心率增加而增大；② 当ε>30%时，直接阻尼系数Cxx≠Cyy，且Cyy>Cxx；③ 直接阻尼系数对涡动频率依赖性较低，涡动频率变化时，直接阻尼系数变化几乎可以忽略不计。由图7(c)、(d)可知：当ε>50%时，不同方向交叉阻尼系数不同，且Cxy的绝对值增量较大。

图8给出了非阻塞状态不同偏心工况下，涡动频率对密封有效阻尼系数的影响。当f>60 Hz时，随偏心率的增加密封有效阻尼系数不断增大，密封稳定性增强。在低频涡动下(f<60 Hz)，密封有效阻尼系数随着偏心的增加而减小，密封稳定性降低。当ε=80%，f<25 Hz时，密封有效阻尼系数表现为负值，可能导致密封失稳。

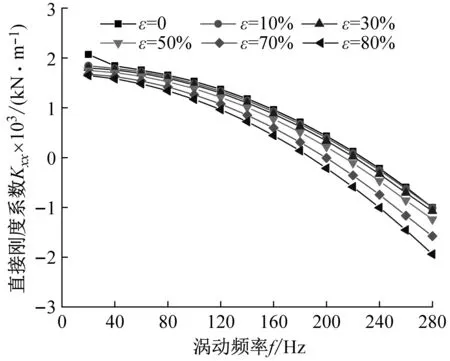
(a) 直接刚度系数Kxx

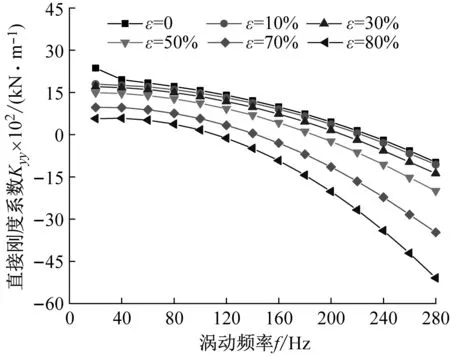
(b) 直接刚度系数Kyy

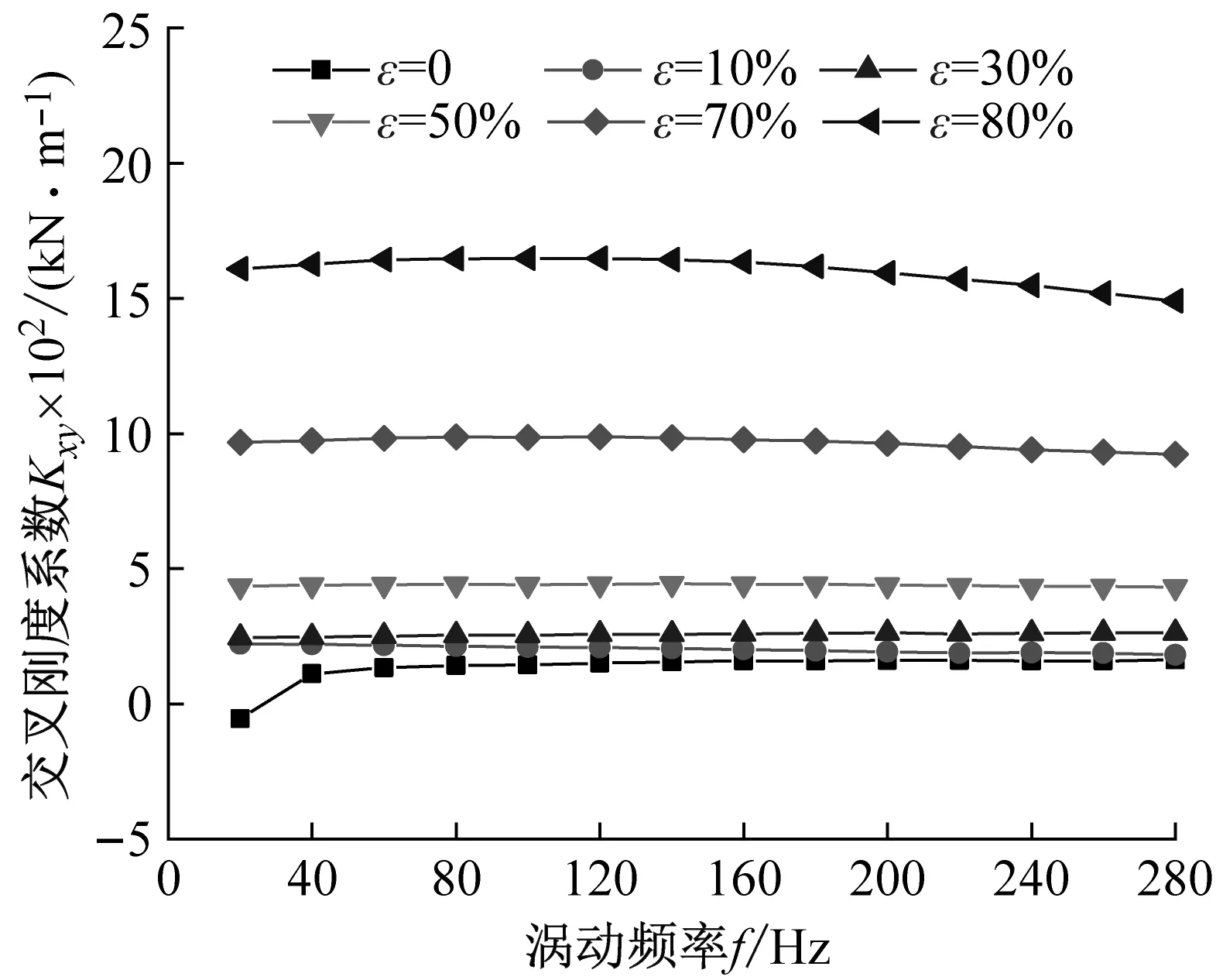
(c) 交叉刚度系数Kxy

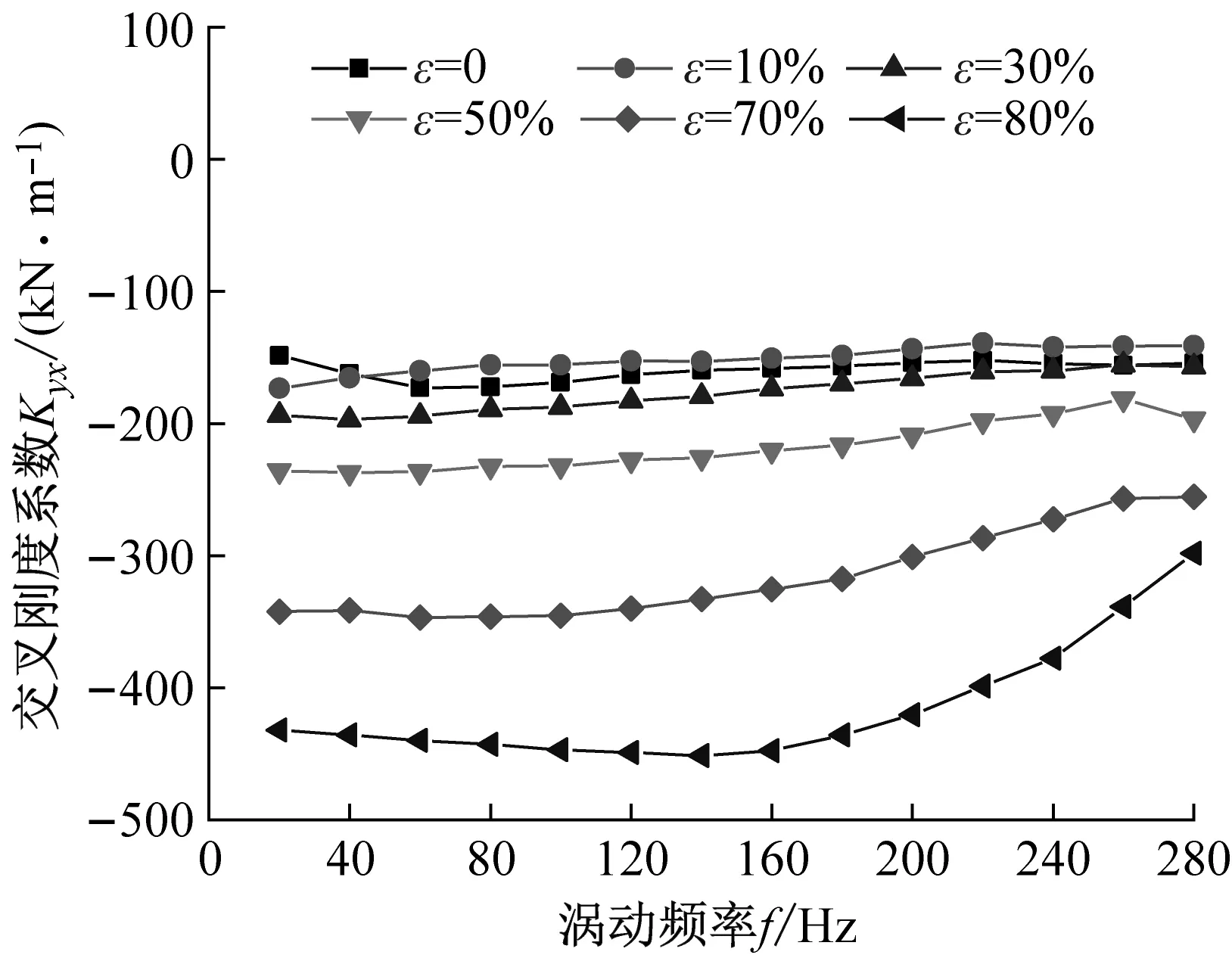
(d) 交叉刚度系数Kyx图6 非阻塞状态不同偏心工况密封刚度系数变化趋势Fig.6 Stiffness coefficient vs. whirling frequency (Unchoked flow condition)

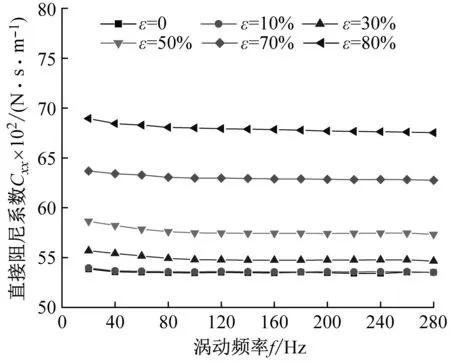
(a) 直接阻尼系数Cxx

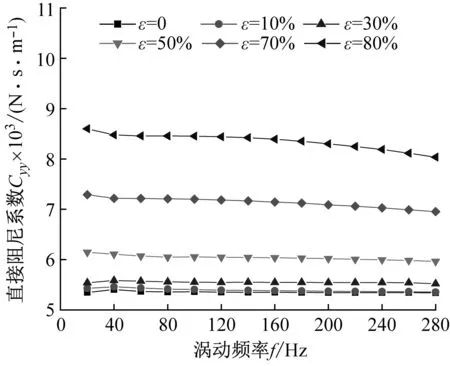
(b) 直接阻尼系数Cyy

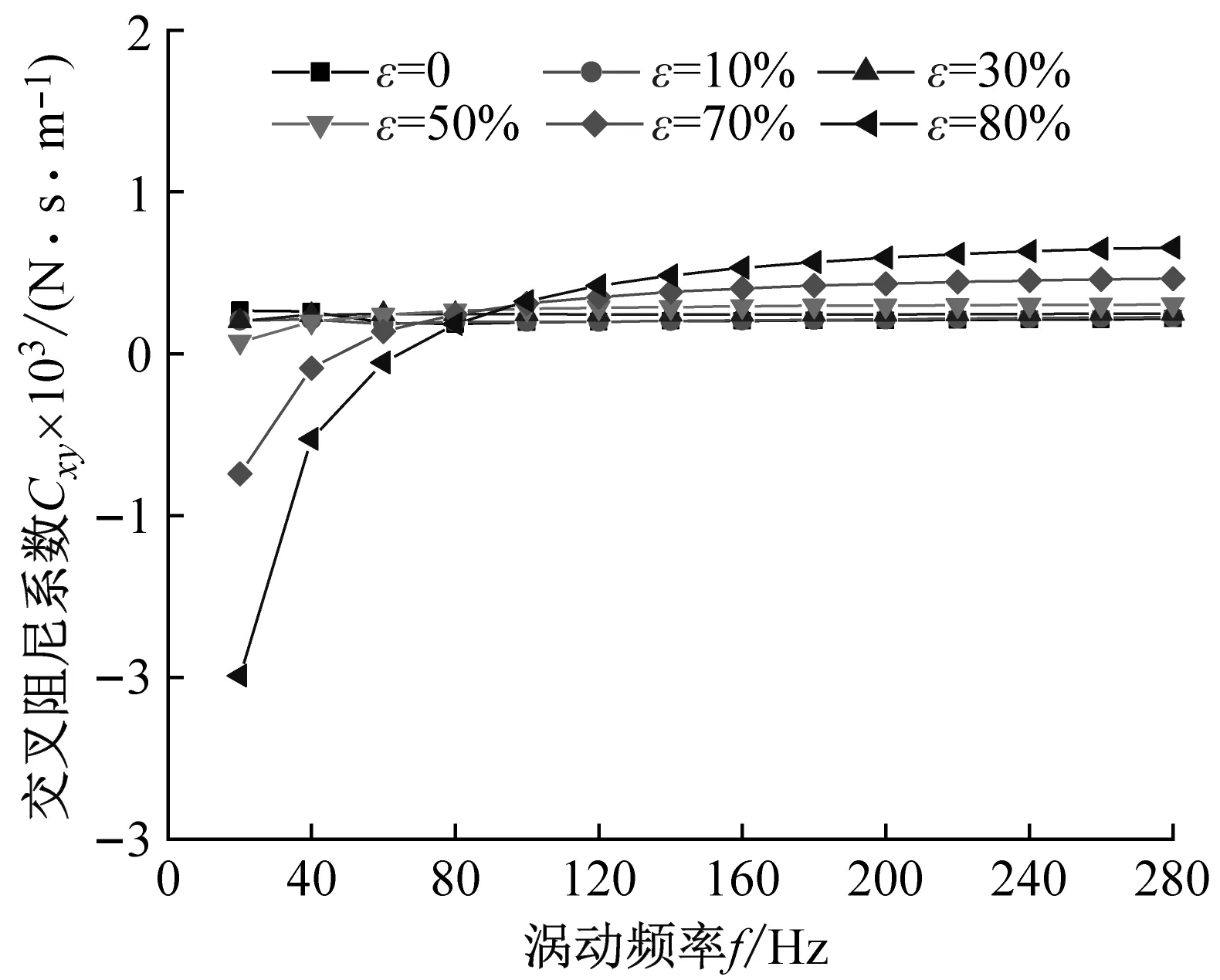
(c) 交叉阻尼系数Cxy

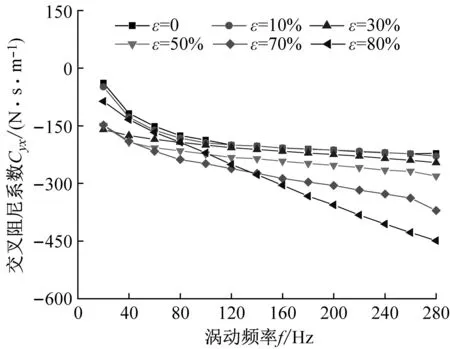
(d) 交叉阻尼系数Cyx图7 非阻塞状态不同偏心工况密封阻尼系数变化趋势Fig.7 Damping coefficient vs. whirling frequency (Unchoked flow condition)

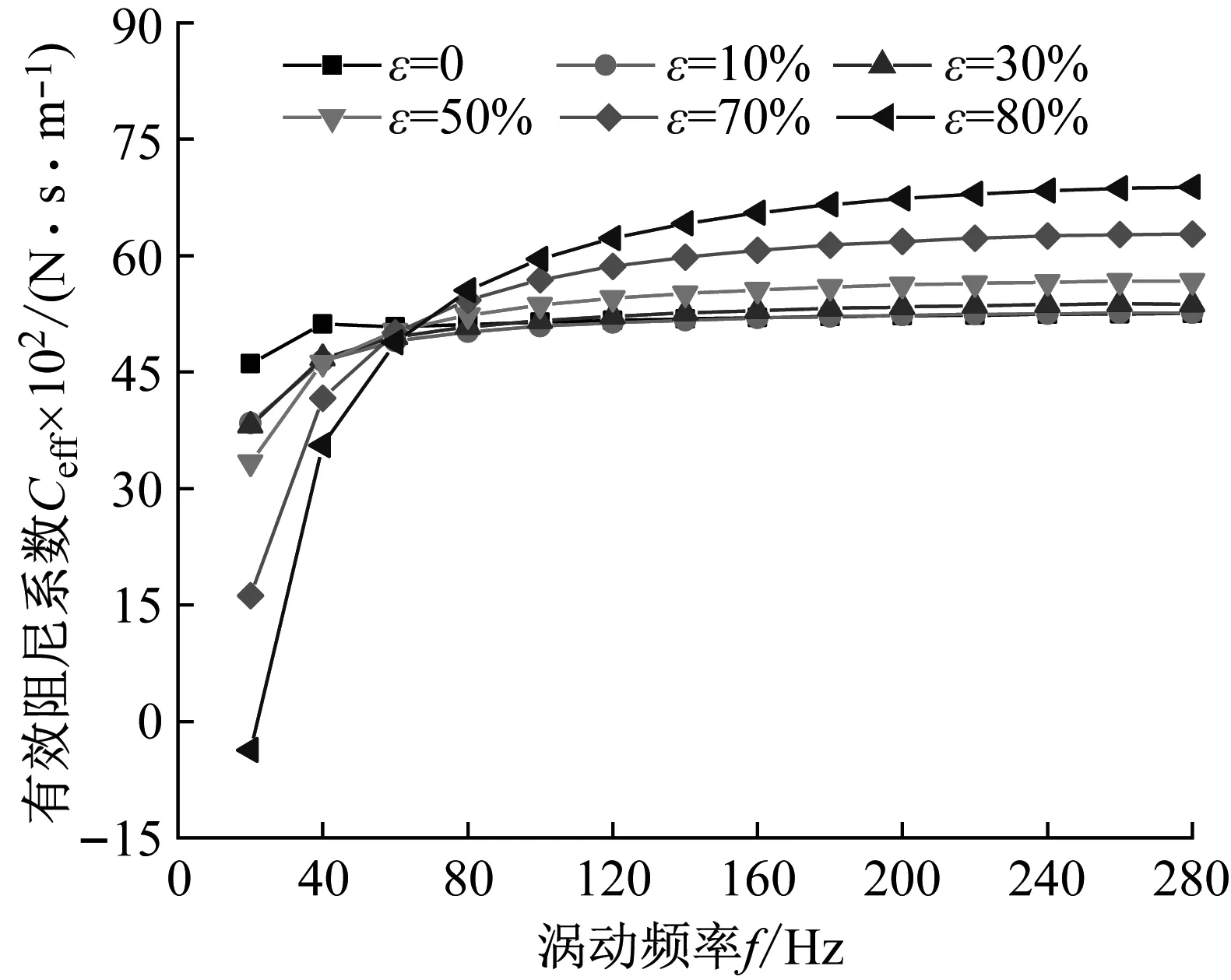
图8 非阻塞状态不同偏心工况密封有效阻尼系数变化趋势Fig.8 Effective damping coefficient vs. whirling frequency (Unchoked flow condition)

2.2.2 阻塞状态密封流动特性

阻塞状态不同偏心工况下，涡动频率与密封刚度系数的关系如图9所示。由图9(a)、(b)可以看出：① 密封直接刚度系数恒为负值，且随偏心率的增加不断减小；② 当ε>30%时，直接刚度系数Kxx≠Kyy，且Kyy的绝对值大于Kxx；③ 当偏心率一定时，随涡动频率的增加密封直接刚度系数不断减小，表现较强的频率依赖性。由图9(c)、(d)可知：① 偏心率与密封交叉刚度系数绝对值呈正相关；② 当ε>30%时，交叉刚度系数(-)Kxy≠(+)Kyx，且Kxy的绝对值增量大于Kyx；③ 密封交叉刚度系数对涡动频率依赖性较低，涡动频率变化，密封交叉刚度系数变化可忽略不计。

图10给出了阻塞状态不同偏心工况密封阻尼系数随涡动频率的变化趋势。由图10(a)、(b)所示：① 任意偏心工况密封直接阻尼系数均表现为正值，且整体随偏心率增加而增加；② 当ε>30%时，直接阻尼系数Cxx≠Cyy，且Cyy>Cxx；③ 直接阻尼系数Cyy仅在低频涡动下表现较强的频率依赖性，Cxx频率依赖性较低。由图10(c)、(d)可知：① 小偏心工况下(ε<30%)时，密封交叉阻尼系数对涡动频率依赖性较低，同一偏心率下，涡动频率变化，密封交叉阻尼系数变化几乎可以忽略不计；② 当ε>30%时，不同方向交叉阻尼系数互不相等，且Cxy的绝对值增量大于Cyx，密封交叉阻尼系数对涡动频率的依赖性较强，同一偏心率下，涡动频率变化，密封交叉阻尼系数变化明显，特别是在低频部分。

阻塞状态不同偏心工况密封有效阻尼系数随涡动频率的变化趋势如图11所示。当f>80 Hz时，有效阻尼系数随偏心率增加而增大，密封稳定性增强。在低频涡动下(f<80 Hz)，随着偏心的增加，有效阻尼系数减小，密封稳定性降低。

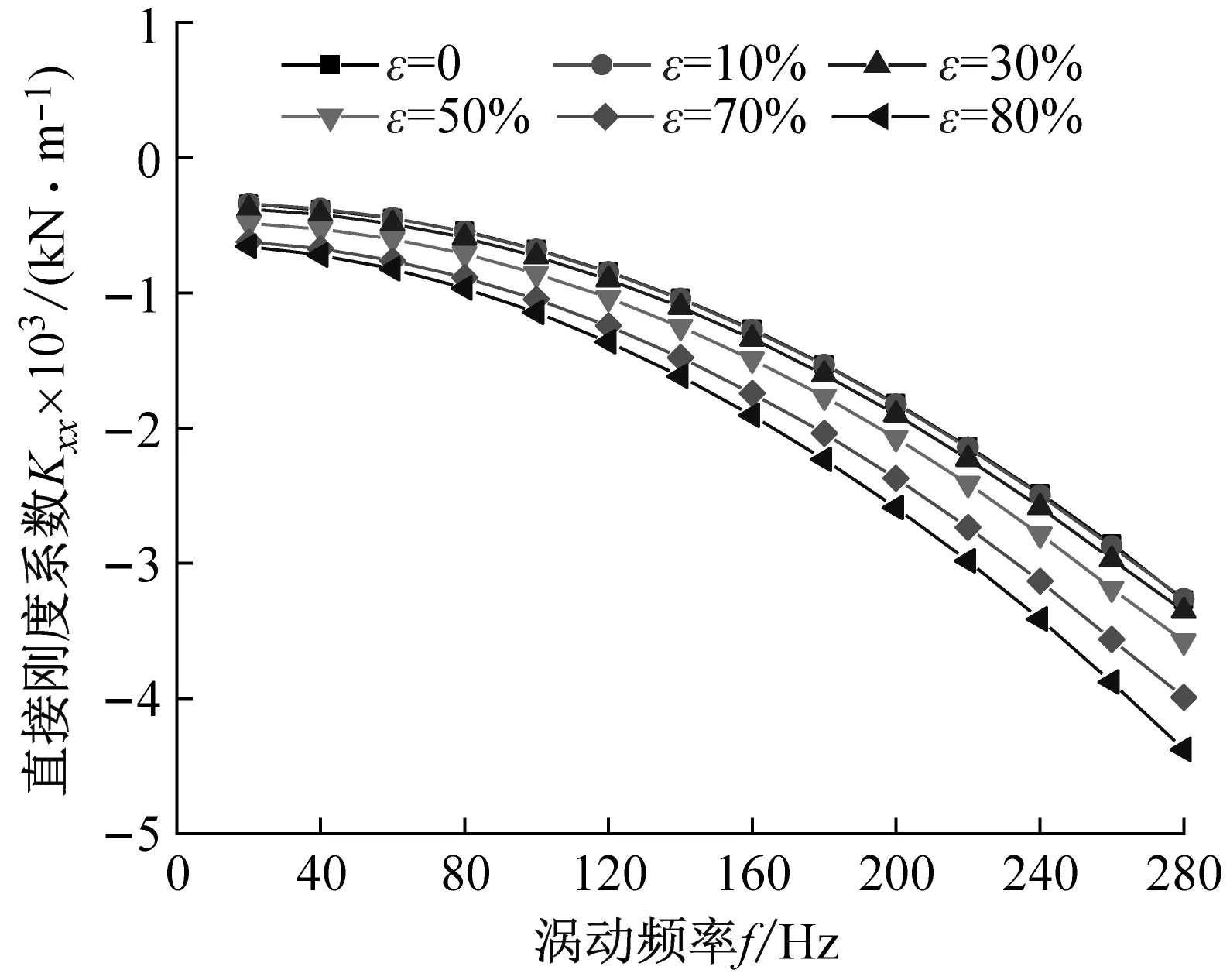
(a) 直接刚度系数Kxx

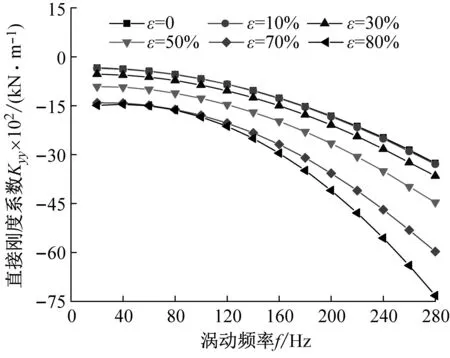
(b) 直接刚度系数Kyy

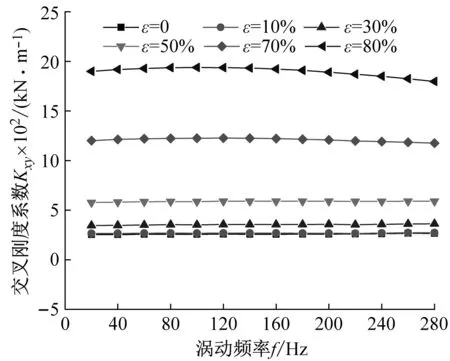
(c) 交叉刚度系数Kxy

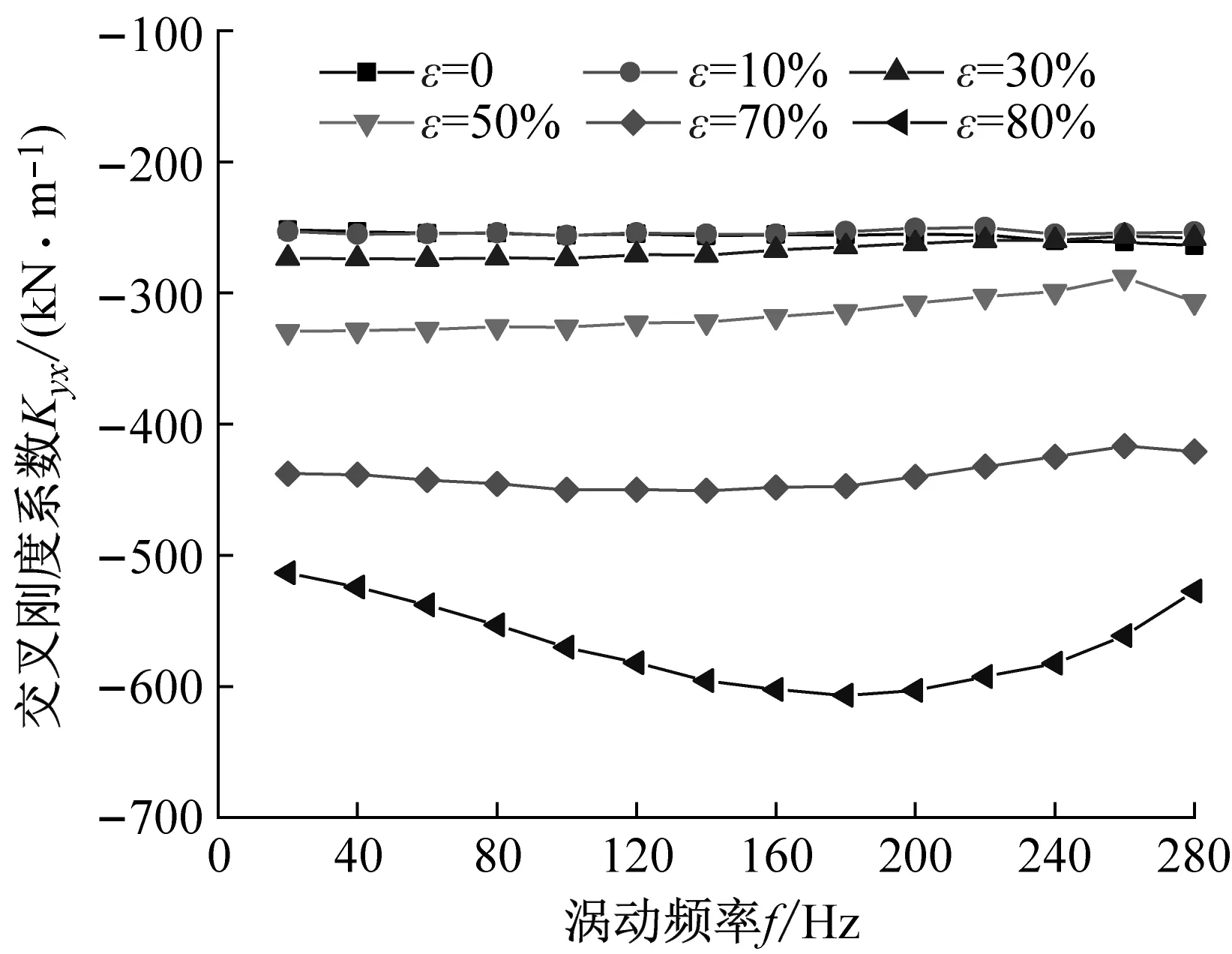
(d) 交叉刚度系数Kyx图9 阻塞状态不同偏心工况密封刚度系数变化趋势Fig.9 Stiffness coefficient vs. whirling frequency (Choked flow condition)

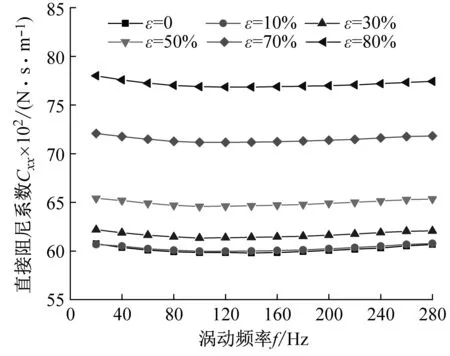
(a) 直接阻尼系数Cxx

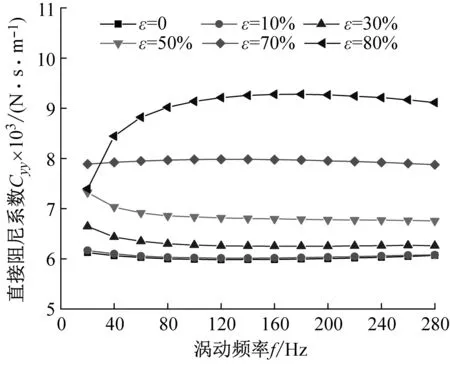
(b) 直接阻尼系数Cyy

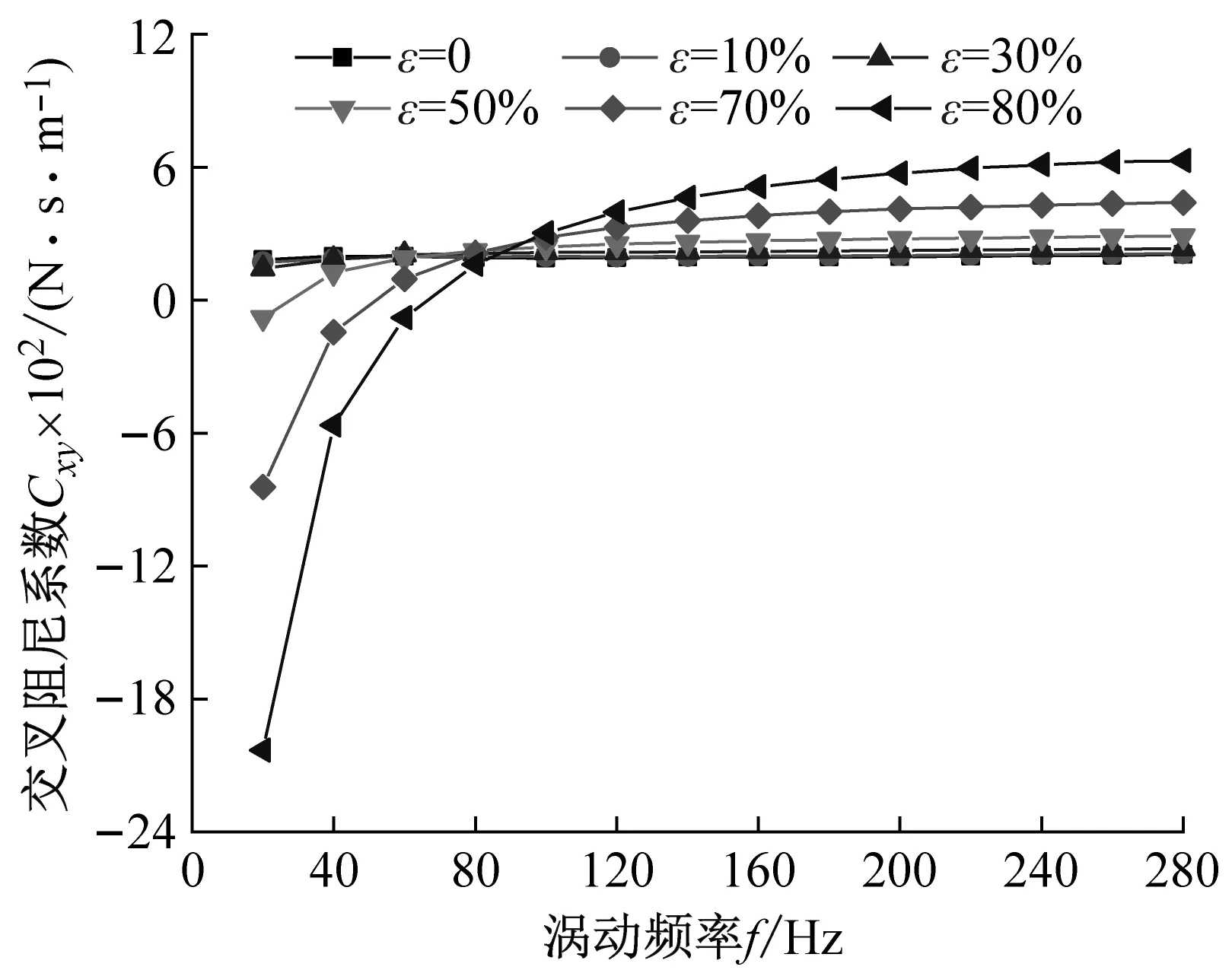
(c) 交叉阻尼系数Cxy

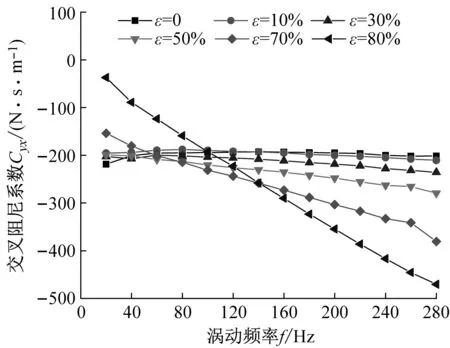
(d) 交叉阻尼系数Cyx图10 阻塞状态不同偏心工况密封阻尼系数变化趋势Fig.10 Damping coefficient vs. whirling frequency (Choked flow condition)

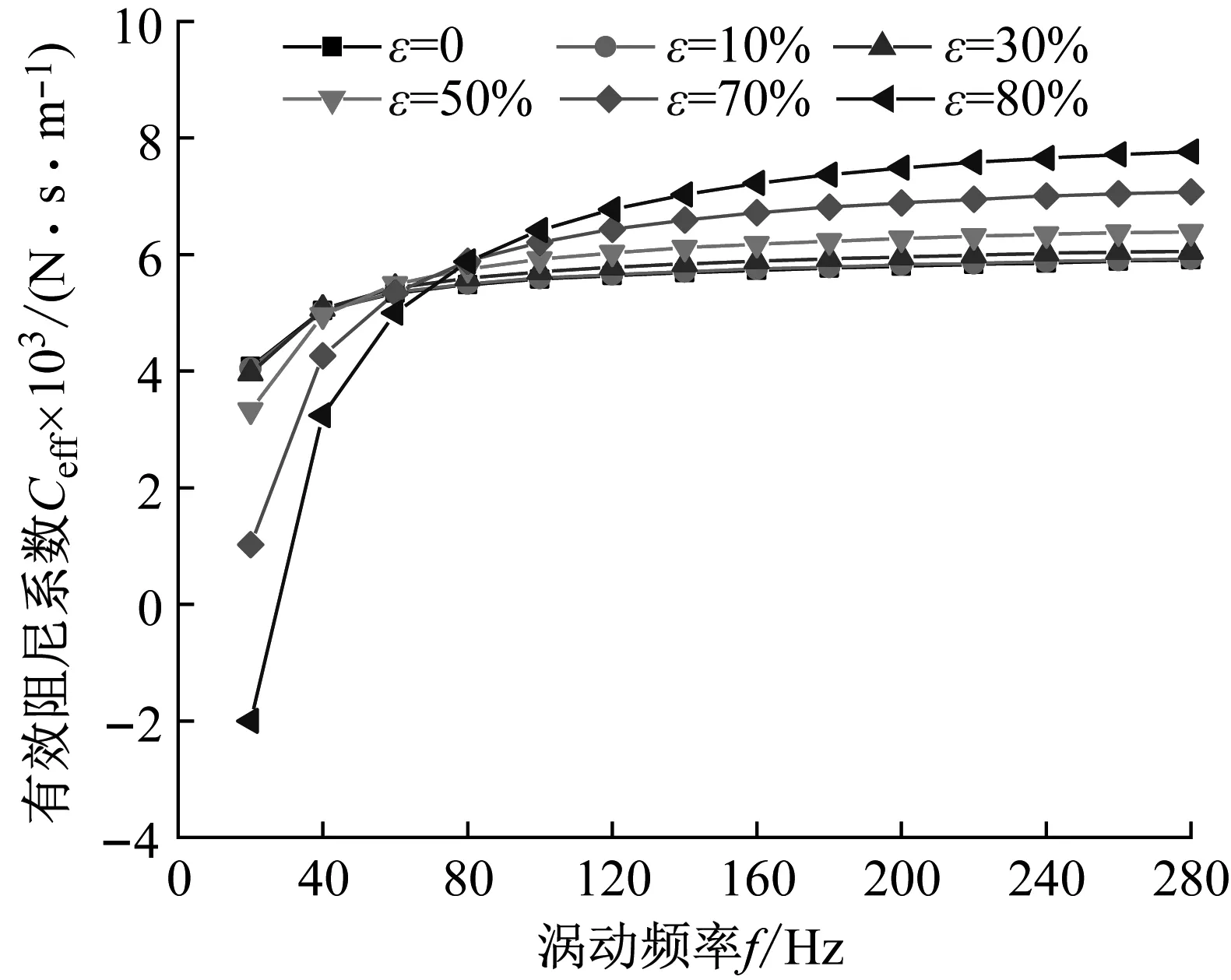
图11 阻塞状态不同偏心工况密封有效阻尼系数变化趋势Fig.11 Effective damping coefficient vs. whirling frequency (Choked flow condition)

2.3 长径比对密封动力特性的影响

对于小扰动模型，引入平均直接、交叉刚度系数Kavg、kavg；平均直接、交叉阻尼系数Cavg、cavg[22- 23]

Kavg=(Kxx+Kyy)/2

kavg=(kxy-kyx)/2

Cavg=(Cxx+Cyy)/2

cavg=(cxy-cyx)/2

(11)

2.3.1 非阻塞状态密封流动特性

图12(a)为非阻塞状态不同长径比密封平均直接刚度随涡动频率的变化趋势，可以看出：① 当L/D=0.5时，平均直接刚度系数恒正，且与偏心率呈负相关；② 相同偏心率下，密封平均直接刚度系数随长径比增加而减小；③ 在同一长径比下，随偏心率增加密封平均直接刚度系数减小；④ 密封平均直接刚度系数对频率依赖性较高，同一长径比及偏心工况下，涡动频率越大，密封平均直接刚度系数越小，密封系统刚度降低。

图12(b)为非阻塞状态不同长径比密封平均交叉刚度系数随涡动频率的变化趋势，可以看出：① 在同一偏心工况下，密封平均交叉刚度系数随长径比增加而增加；② 在同一长径比下，偏心率与密封平均交叉刚度系数呈正相关；③ 密封平均交叉刚度系数对频率依赖性较低，转子涡动频率变化，交叉刚度系数变化可忽略。

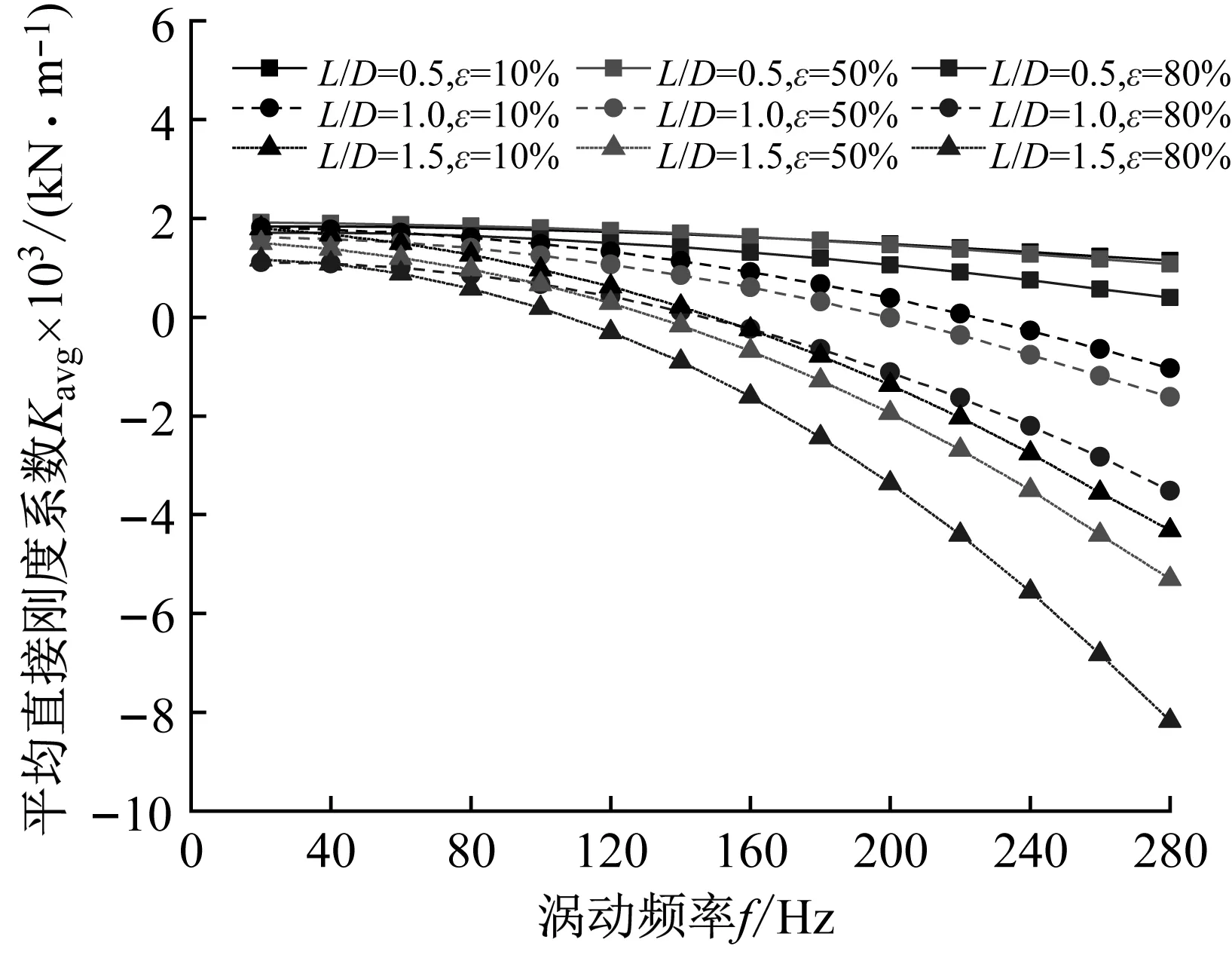
(a) 平均直接刚度系数Kavg

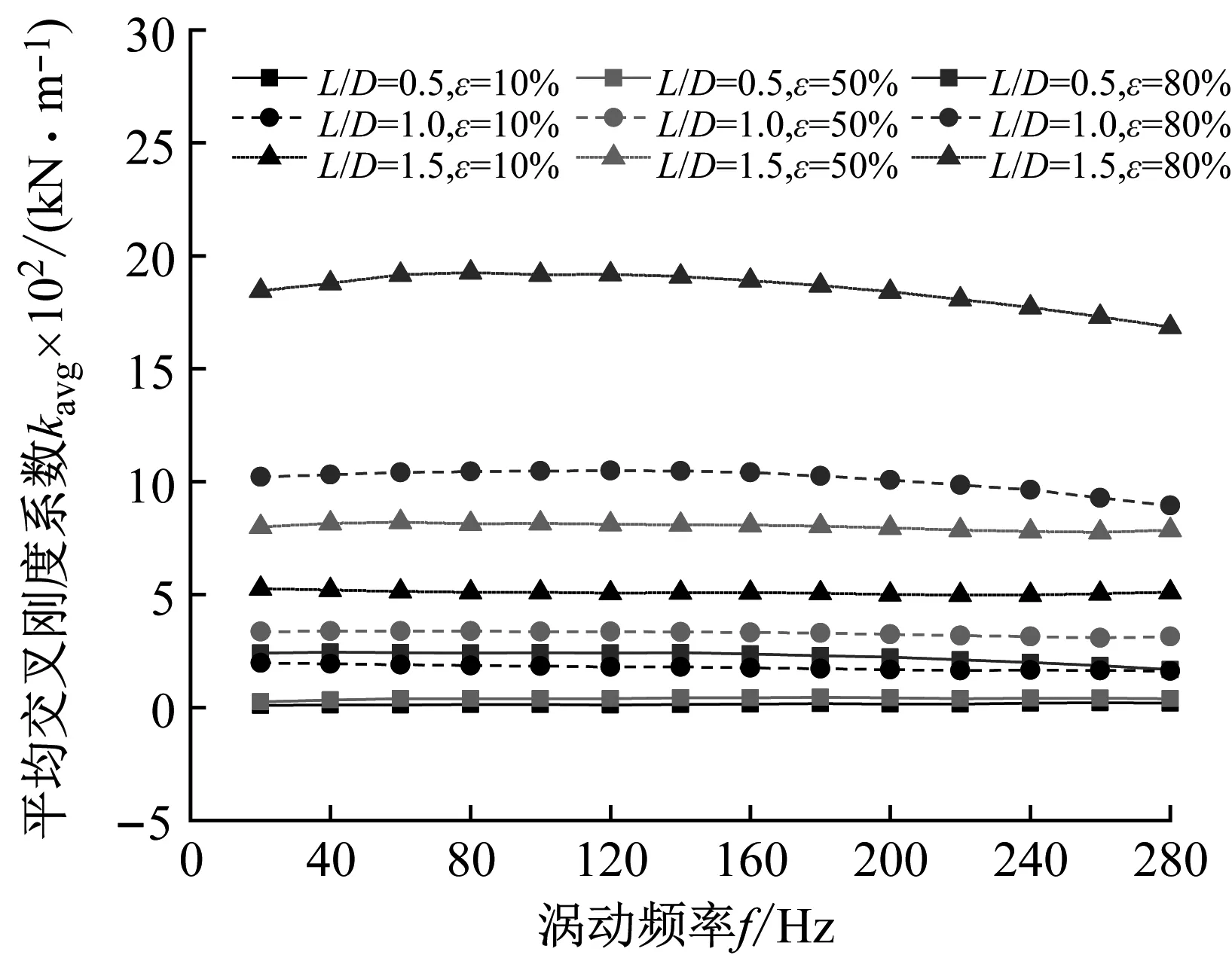
(b) 平均交叉刚度系数kavg图12 非阻塞状态下不同长径比密封平均刚度系数Fig.12 Average stiffness coefficient vs. whirling frequency (Unchoked flow condition)

非阻塞状态不同长径比下，随涡动频率密封平均直接阻尼系数的变化趋势如图13(a)所示：① 在同一偏心工况下，随着长径比的增加，密封平均直接阻尼系数增加；② 在同一长径比下，随偏心率的增加，密封平均直接阻尼系数增大；③ 在低频涡动(f<80 Hz)时，密封平均直接阻尼系数对频率依赖性较大。

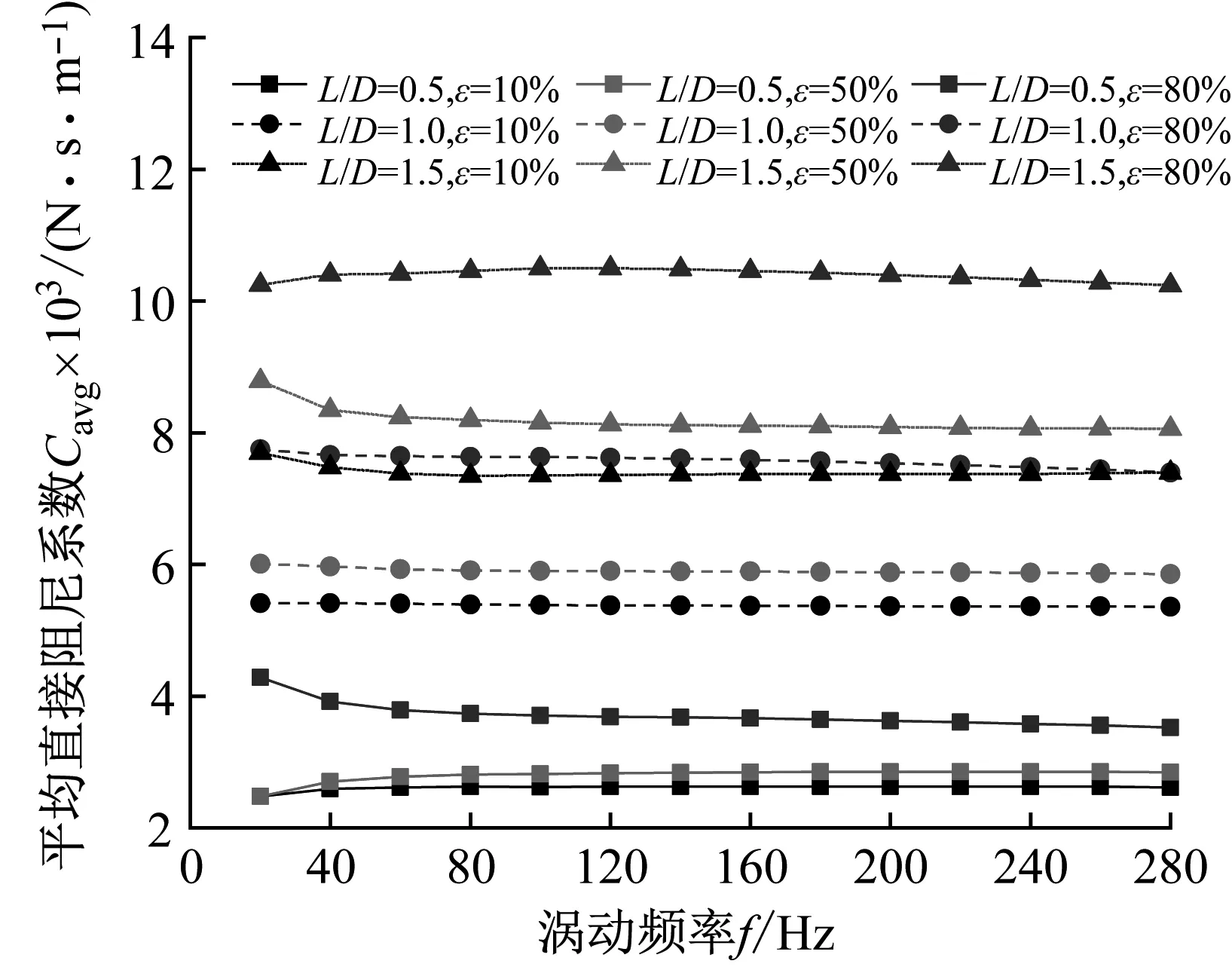
(a) 平均直接阻尼系数Cavg

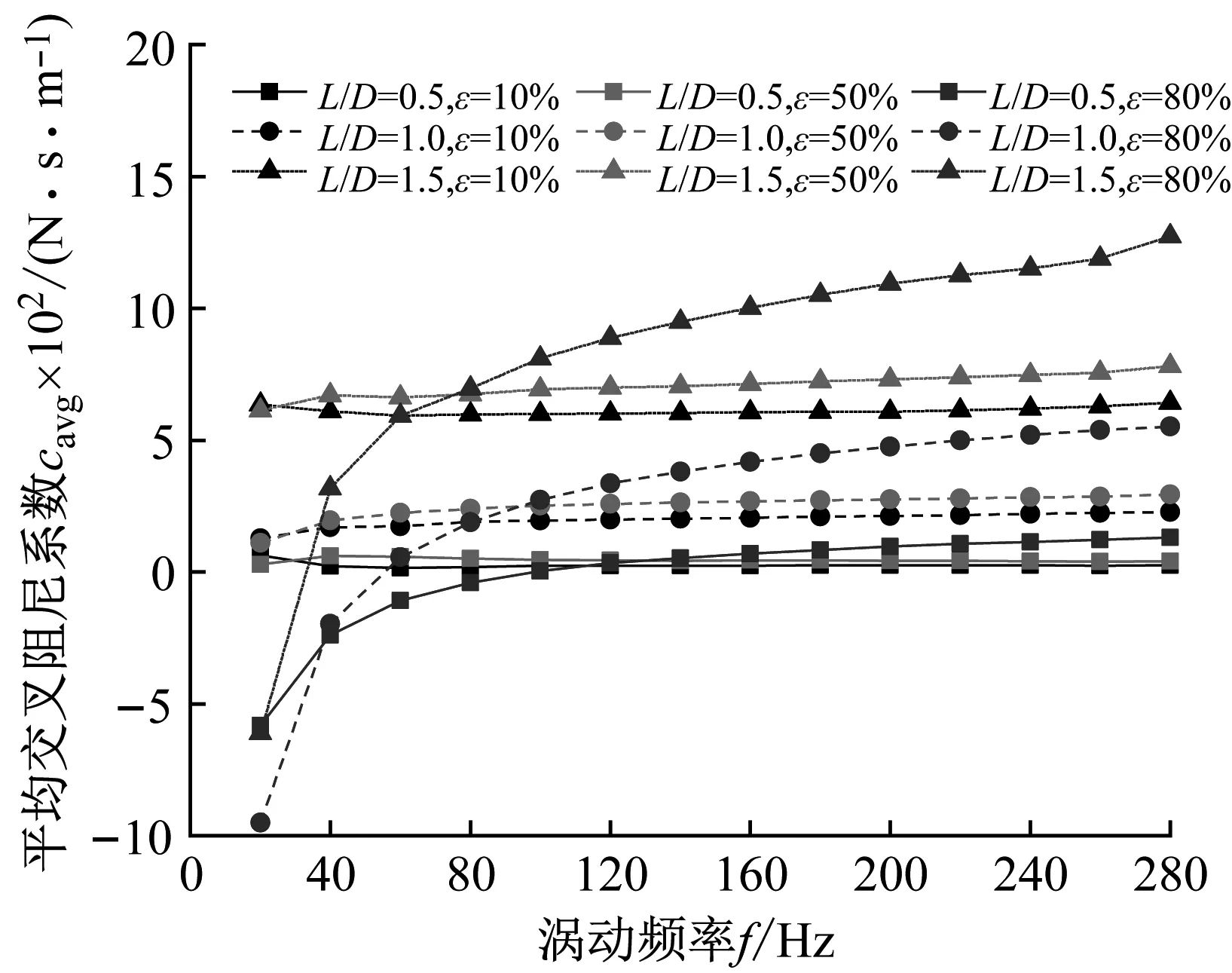
(b) 平均交叉阻尼系数cavg图13 阻塞状态下不同长径比密封平均阻尼系数Fig.13 Average damping coefficient vs. whirling frequency (Unchoked flow condition)

图13(b)为非阻塞状态不同长径比密封平均交叉阻尼系数随涡动频率的变化趋势，小长径比密封(L/D=0.5)对频率依赖性较低，随着偏心率及长径比的增大，密封平均交叉阻尼系数对频率依赖性增强。

在非阻塞、不同长径工况下，密封有效阻尼系数随涡动频率的变化趋势如图14所示。结果表明：① 当f>40 Hz时，同一偏心工况下，有效阻尼系数随长径比增加而增大，密封系统稳定性增强；当f<40 Hz时，有效阻尼系数随长径比增加而减小；在低涡动频率下(f<25 Hz)，除小长径比密封(L/D=0.5)外，其余密封有效阻尼系数均为负值，长径比越大，有效阻尼系数越负，导致密封失稳。② 同一长径比下，不同偏心工况的阻尼系数随涡动频率变化曲线增量不同，因此，存在有效阻尼系数相同的交叉点，交叉点之前，密封有效阻尼系数随偏心率增加而减小，系统稳定性降低；交叉点之后，密封有效阻尼系数随偏心率增加而增大，稳定性增强。

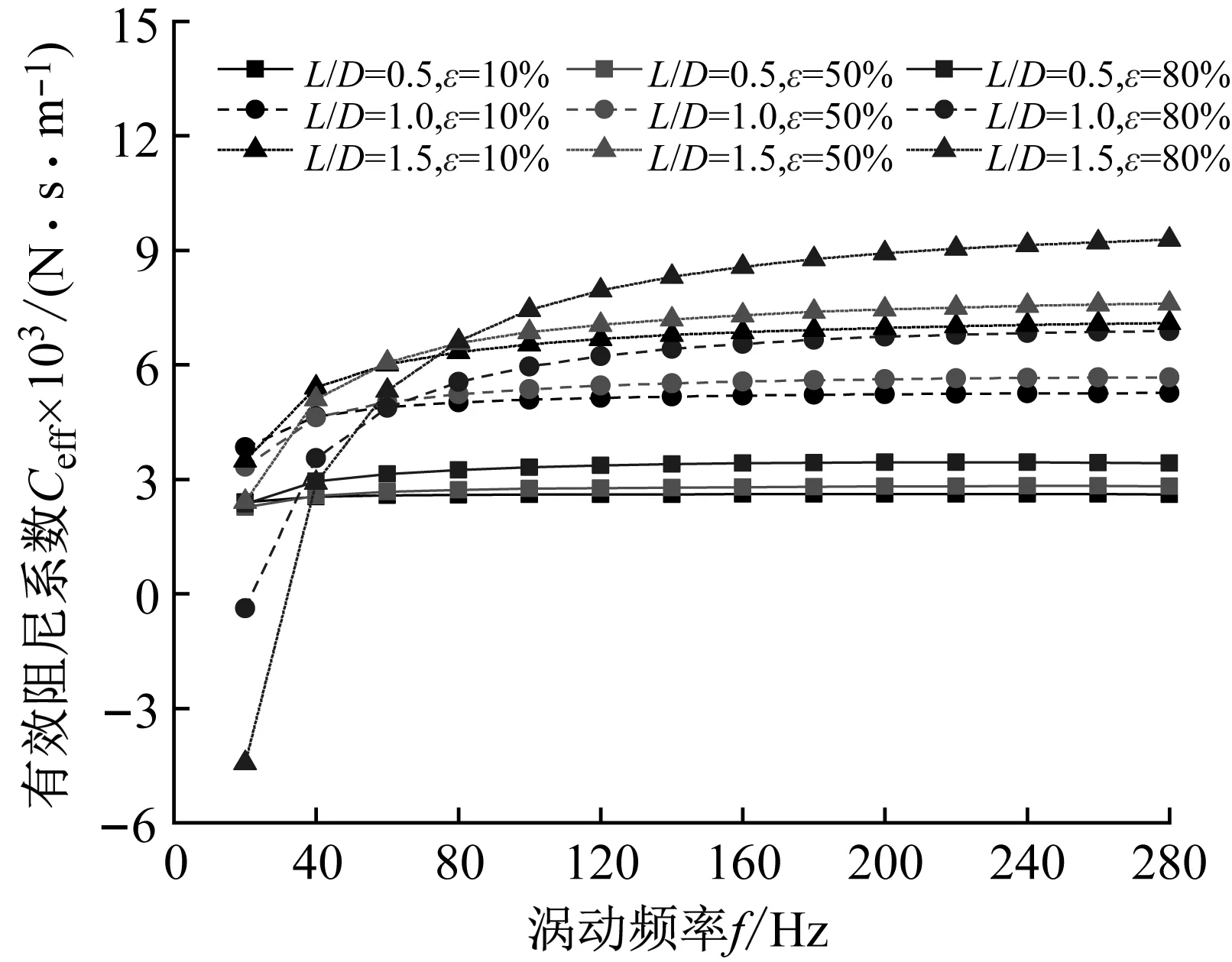
图14 非阻塞状态下不同长径比密封有效阻尼系数变化趋势Fig.14 Effective damping coefficient vs. whirling frequency (Unchoked flow condition)

2.3.2 阻塞状态密封流动特性

图15(a)为阻塞状态不同长径比密封平均直接刚度随涡动频率的变化趋势，可以看出：① 小长径比密封(L/D=0.5)、ε<50%时，密封平均直接刚度系数表现为正值，密封系统刚度增加；② 在同一偏心工况下，长径比越大密封平均直接刚度系数越小；③ 在同一长径比下，密封平均直接刚度系数随偏心率增加而减小；④ 随着长径比的增加，密封平均直接刚度系数对频率依赖性增强，涡动频率越大，密封平均直接刚度系数越小，密封系统刚度降低。

图15(b)为阻塞状态不同长径比平均交叉刚度系数变化趋势，可以看出：① 在同一偏心工况下，密封平均交叉刚度系数随长径比增加而增加；② 在同一长径比下，偏心率与密封平均交叉刚度系数呈正比；③ 密封平均交叉刚度系数对频率依赖性较低，转子涡动频率变化，交叉刚度系数变化可忽略。

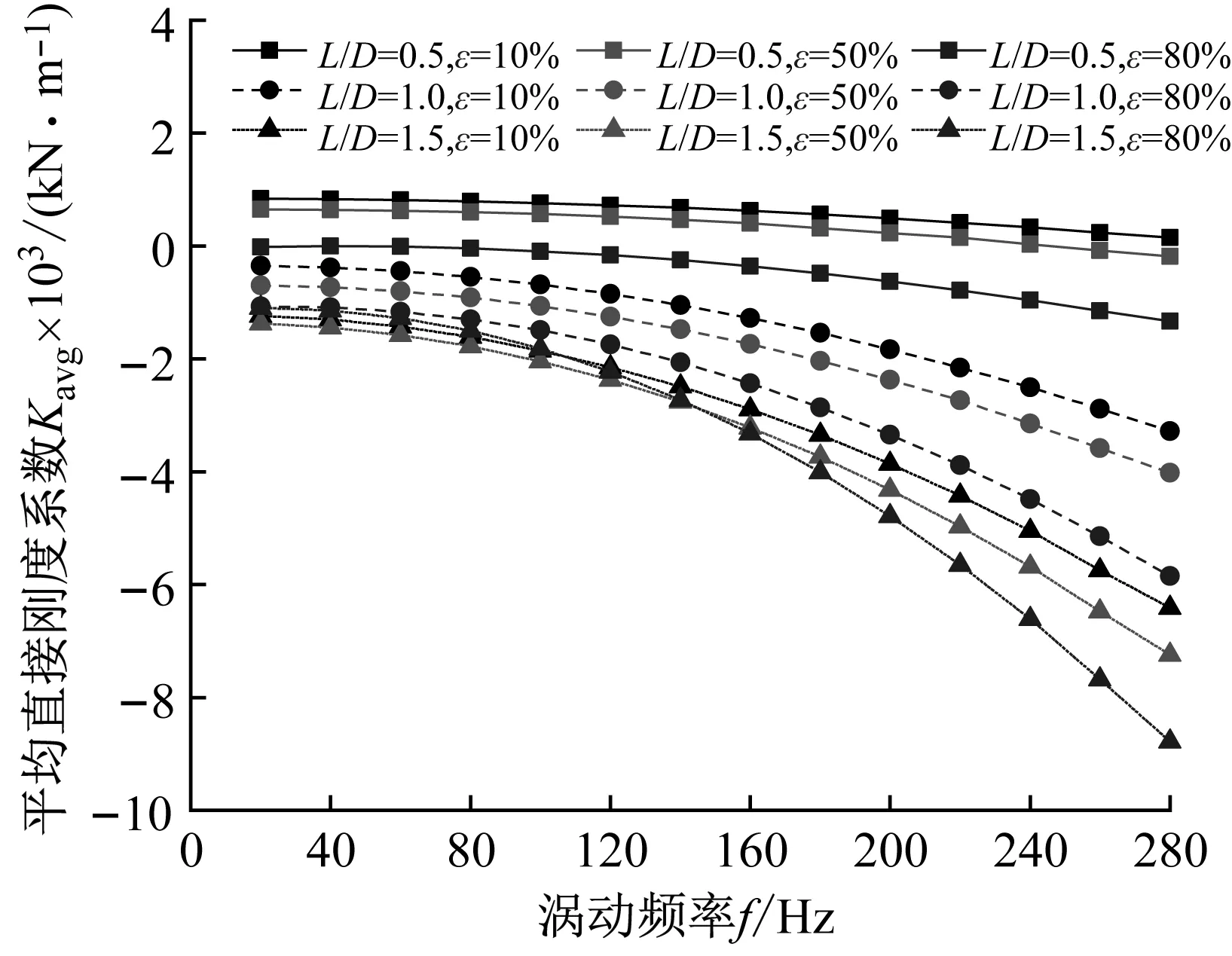
(a) 平均直接刚度系数Kavg

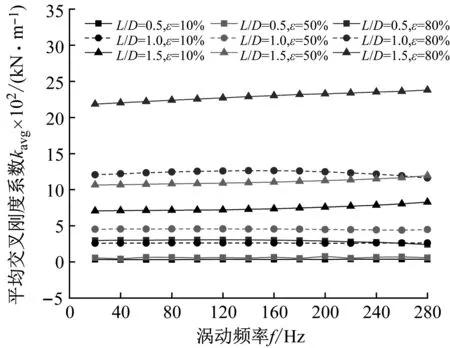
(b) 平均交叉刚度系数kavg图15 阻塞状态下不同长径比密封平均刚度系数Fig.15 Average stiffness coefficient vs. whirling frequency (Choked flow condition)

图16(a)为阻塞状态不同长径比密封平均直接阻尼系数变化趋势，可以看出：① 在同一偏心工况下，随着长径比的增加，密封平均直接阻尼系数增加；② 在同一长径比下，随着偏心率的增加，密封平均直接阻尼系数增大；③ 在低频涡动(f<80 Hz)时，密封平均直接阻尼系数对频率依赖性较大。

图16(b)为阻塞状态不同长径比密封平均交叉阻尼系数变化趋势，小长径比密封(L/D=0.5)对频率依赖性较低，随着偏心率及长径比的增大，密封平均交叉阻尼系数对频率依赖性增强。

阻塞状态不同长径比密封有效阻尼系数变化趋势如图17所示。当f>40 Hz时，同一偏心工况下，有效阻尼系数随长径比增加而增大，密封系统稳定性增强；当f<40 Hz时，有效阻尼系数随长径比增加而减小；在低涡动频率下(f<25 Hz)，除小长径比密封(L/D=0.5)外，其余密封有效阻尼系数均为负值，长径比越大，有效阻尼系数越负，密封-转子系统失稳。

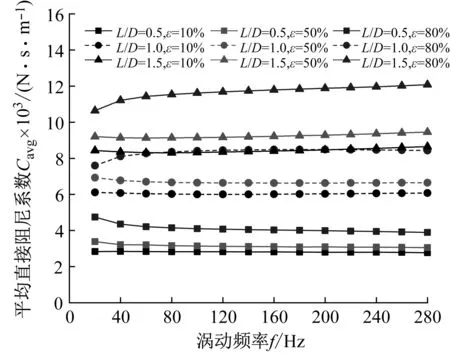
(a) 平均直接阻尼系数Cavg

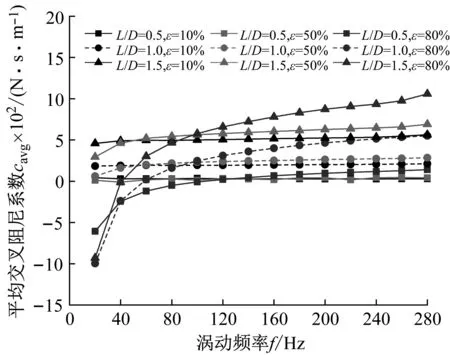
(b) 平均交叉阻尼系数cavg图16 阻塞状态下不同长径比密封平均阻尼系数Fig.16 Average damping coefficient vs. whirling frequency (Choked flow condition)

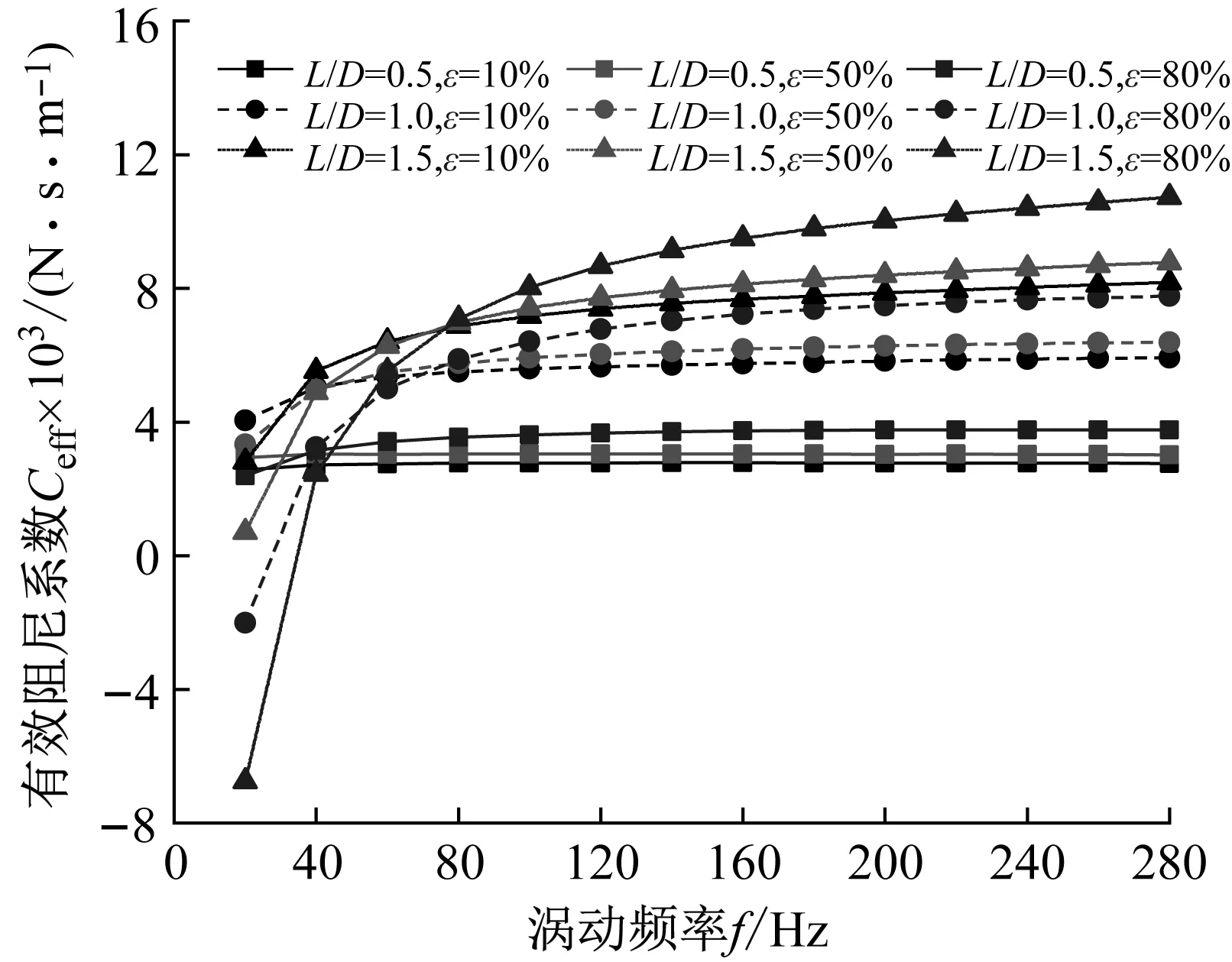
图17 阻塞状态下不同长径比密封有效阻尼系数变化趋势Fig.17 Effective damping coefficient vs. whirling frequency (Choked flow condition)

3 结 论

本文基于微元理论方法识别光滑环形气体密封动力特性系数，计算密封在2种出口状态、5种偏心率及3种长径比下密封动力特性系数，得到以下结论：

(1) 在非阻塞与阻塞状态下(L/D=1.0)，密封直接刚度系数均随偏心率及涡动频率的增加而减小。非阻塞状态下，密封直接刚度系数存在由正值到负值的转变；而阻塞状态密封直接刚度系数恒为负值。

(2) 试验密封(L/D=1.0)交叉刚度系数绝对值与直接阻尼系数均随偏心增加而增大；当ε>30%时，|Kyy|>|Kxx|、|Kxy|>|Kyx|、|Cyy|>|Cxx|、|Cxy|>|Cyx|，且随着偏心增加，差距越大。因此，密封在高偏心情况下，必须考虑偏心率对密封特性系数的影响，不能简化为传统的四个动力特性系数。

(3) 密封有效阻尼系数与涡动频率及偏心率相关。高涡动频率下，有效阻尼系数随偏心率增加而增大；低涡动频率下，有效阻尼系数随偏心率增加而减小。因此，低频涡动、高偏心转子系统更容易失稳。

(4) 随长径比的增加，密封平均直接刚度系数减小，密封系统刚度降低，平均交叉刚度系数增大，平均直接阻尼系数增加。密封有效阻尼系数与长径比及涡动频率相关，高涡动频率下，有效阻尼系数随长径比增加而增大，密封系统稳定性增强；低涡动频率下，有效阻尼系数随长径比增加而减小，密封系统稳定性降低；长径比越大，密封越易失稳。