基于改进堆栈自编码的诊断错误标签修正
2022-01-27黄亦翔肖登宇刘成良李怀洋
张 旭, 黄亦翔, 张 轩, 肖登宇, 刘成良, 李怀洋, 朱 涛
(1.上海交通大学 机械系统与振动国家重点实验室,上海 200240;2.徐州重型机械有限公司 高端工程机械智能制造国家重点实验室,徐州 221004)
随着物联网的发展和机械检测设备的密布,利用大数据进行故障诊断成为现代工业发展的重要方向之一。监督学习中,正确的标签样本是诊断的基础,但标记错误的标签会降低诊断的精度和泛化能力。在实际工程中,错误标签的情况难以避免。
数据采集后,试验工作人员会根据需要给数据设置标签以便于使用,而标签的设置依赖于操作人员的水平。故障类型,故障程度的诊断会因为标准不同而造成标签不够准确,甚至错误。数据本身也会存在限制条件,如多故障的齿轮箱,因为裂纹而忽视了其他故障;缓慢变化的故障在前期被认为是正常等。另外,在信号转换,通信传输,预处理中的程序错误也会造成错误标签的产生[1]。
Quinlan[2]证明,相对于数据本身的特征噪声,错误的标签对于分类器影响更大。现有算法,如KNN,决策树,AdaBoost等在进行故障诊断时,容易受到错误标签的负面影响[3],Zhang等[4]也发现深度模型会拟合随机标签,进而影响预测结果的准确性。因此,对原始数据标签进行修正有助于提高数据的可信程度,从而提升模型的泛化能力。
基于以上原因,错误标签的研究受到了国内外各个领域学者的广泛关注和研究。错误的标签样本多被认为是异常点,常采用过滤筛选方式剔除异常标签,以降低错误标签率。罗俊杰等[5]将Bayes分类器获取的样本信息熵作为样本归属的判断依据,从而筛选异常样本。高琼[6]采用KNN聚类后的样本类别概率来判断样本归属。为了保持样本中正确标签的流形结构,Liu等使用保持流形稀疏图(MSPA)的方法来过滤错误标签,夏建明等[7]结合稀疏流行聚类模型(SMCE)和KNN聚类结果确定样本的真实标签。上述方法多假设原有正确样本具有一定流形结构,方法准确性易受到样本分布的影响。因此,有学者在提升现有方法的鲁棒性方面进行研究。Liu等[8]首先证明了损失函数加权方法在错误标签中的重要性,并提出了给定错误标签数据分布和变化矩阵情况下的权重计算方法。对于标签未知或不确定的数据,常采用聚类获取伪标签以帮助训练的方法。深度聚类[9],根据聚类结果建立混合信息增益比参数以降低错误标签影响[10]等方法均是如此。除此以外,刘艺[11]结合知识图谱对训练数据权重进行调整。Jiang等[12]提出了基于数据的导师网络来监督学生深层网络训练,并提供样本训练权重。Han等[13]训练两个并行神经网络,利用小损失的数据进行下一轮交叉训练。上述方法多采取提高正确标签权重,剔除错误标签影响的方式,需要大量数据样本,并且会舍弃一部分数据样本,减少了数据中的信息量。针对于神经网络会优先记忆简单数据,之后记忆复杂数据的特点,Guo等[14]利用数据的分布密度来衡量数据的复杂性,并使用排序后数据依次训练神经网络。Cao等[15]采用双Softmax层进行分类,减少深层模型对错误标签的过度拟合,这些方法同样对训练的数据量提出了一定要求。
在机械故障诊断领域,正确的样本标签是诊断准确度的保证。目前来看,与错误标签相关的机械故障诊断研究较少。针对此问题,本文提出一种基于改进堆栈自编码的错误标签修正方法。该方法通过编码器对样本特征进行映射,利用孤立森林(isolation forest, iFroest)获取降维后样本的伪标签,根据伪标签调整编码器的权重,从而使编码器注重于正确样本。考虑到数据类别导致的区别,利用基于随机森林的交叉验证方法获取样本的信息熵,修正错误标签。试验表明,本文提出的方法可以获得信号的深层特征,而且在多个错误标签比例下均能显著降低样本错误标签率,修正错误标签,提高故障诊断的准确率。
1 错误标签修正原理
1.1 错误标签修正流程
实际工程中,样本数据量少,数据分布未知,单一标签修正方法依赖于数据的分布。因此,本文通过改进堆栈自编码获得一部分错误标签率低的样本,然后用这类数据来训练分类器以实现标签修正,具体流程如图1所示。在提取信号初步特征后,将含有错误标签的样本集输入到堆栈自编码中,获得低维度输出特征。同时使用孤立森林将样本赋予“正确”和“错误”的伪标签,进而调整样本权重,使自编码注重于“正确”标签样本。循环结束后,利用堆栈自编码获得所有样本的低维度特征,通过孤立森林将所有样本分为“正确”样本和“错误”样本两类,并使用所有“正确”标签的样本训练分类器,通过对比分类器下样本的信息熵来进行错误标签的修正。

图1 错误标签修正流程图Fig.1 Noise label correction flow chart
1.2 堆栈自编码神经网络
自编码网络(auto-encoder, AE)由编码器(encoder)和解码器(decoder)两部分组成[16],如图2所示。

(1)
式中:L(x(i),gθ′(fθ(x(i))))为损失函数;n为样本个数。

图2 自编码网络结构Fig.2 Structureof auto-encoder
堆栈自编码神经网络(stacked auto-encoder, SAE)是由多个自编码首尾相连接组成的无监督学习网络,包括一个输入层,一个输出层,多个隐藏层,结构如图3所示。

图3 堆栈自编码结构Fig.3 Structureof stacked auto-encoder
正如前文所说,提高对正确标签样本的关注是降低错误标签样本影响的有效方法,本文在训练时会剔除错误标签的样本对损失函数的影响,只选用正确标签样本所带来的损失,式(1)所对应的优化函数更新为
(2)
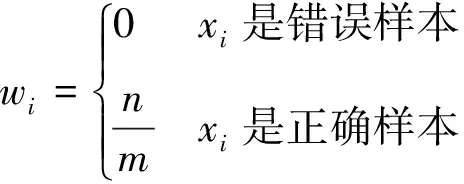
(3)
式中:n为所有样本个数;m为伪标签为“正确”的样本个数;wi为基于伪标签的权重。
1.3 孤立森林
孤立森林(iForest)是基于隔离树(iTree)的集成快速异常点检测方法,能够准确检测出分布稀疏且距离大密度群体远的异常点[17]。
对于维度为d的n个样本数据X={x1,x2,…,xn},表1给出了构建iTree的具体方法。
相对于正常点,异常点距离根节点的路径较短。对多个iTree中点x的平均路径进行计数,将结果记作E(h(x)),其中h(x)代表x的平均路径长度。

表1 iTree的构建方法
对于有n个点的X,样本x的异常分数可以表示为
(4)
其中c(n)为n个样本的平均搜索路径长度,用来归一化E(h(x))。
异常分数越接近1,x为异常样本的可能性越大。在堆栈自编码每次循环中,iForest用于给样本赋予伪标签,调整堆栈自编码对样本的权重。其次,在所有循环结束后,iForest根据预先设置的错误标签比例η,将样本分为正确标签样本和错误标签样本两类。
1.4 基于信息熵的标签修正
信息熵是对样本类别不确定性进行评估的有效方法[18]。类别数为k的样本集中,样本x属于类别i的概率为Pi(x),则x的信息熵H(x)表示为
(5)
当所有可能相等时,信息熵最大,属于完全不确定的情况;当其中一种情况的概率为1,其他为0时,信息熵H(x)取到最小值0,此样本被称为典型样本。在样本标签修正中,如果样本是典型的,则使用预测的标签作为此轮中样本的最终标签。
k折交叉验证方法将数据集D划分成为k个大小相似的互斥集合,然后使用k-1个子集作为训练集,剩下的子集作为验证集,共进行k次训练和测试。图4是本文5折交叉验证的示意图。

图4 5折交叉验证Fig.4 5-fold cross-validation
在堆栈自编码中,孤立森林会选择出“正确”标签样本和“错误”标签样本。
本文的交叉验证主要分为两部分。在第一轮训练中,“正确”样本为训练数据,“错误”样本为测试数据。对于“错误”标签样本,默认其原始标签是错误的,选取五次预测结果中的出现次数最多的标签(相同取平均信息熵小的标签)作为其预测标签;对于“正确”标签样本,通过分类概率获取样本的信息熵,当信息熵小于信息熵阈值β时,认为该样本是典型样本,将预测标签作为样本的标签。
在第二轮及以后的轮次中,将“正确”标签样本与“错误”标签样本合起来作为数据集D′,进行交叉验证,并基于信息熵修正样本标签。
2 试验验证
齿轮是机械设备的核心部件之一,随着工业需求的提高,人们对齿轮的可靠性也提出了更高的要求。本文以不同故障的齿轮为对象,人工生成错误标签数据来验证方法的可行性。
2.1 试验设置
实际工程会因为时间、成本、安全性等原因,较少在有故障零部件的情况下进行工作并采集数据,所以采用动力传动故障诊断试验台来获得齿轮故障数据以进行试验。如图5所示,试验台包含行星齿轮箱,平行轴齿轮箱,负载控制器以及磁力制动器等设备。测试齿轮健康状态分5类,分别是正常、磨损、缺齿、断齿、齿根裂纹,图6是部分故障齿轮图片。

图5 齿轮故障试验台Fig.5 Test system for gear fault

(a) 磨损齿轮

(b) 缺齿齿轮

(c) 断齿齿轮图6 故障齿轮Fig.6 Faulty gear
试验使用加速度传感器采集齿轮箱振动信号,采集频率为10 kHz,电机输入转速为15 Hz,每类齿轮采集500 s数据,各类齿轮的时域波形如图7所示。

图7 齿轮时域波形Fig.7 Timedomainwaveformof gear
2.2 数据预处理
选取振动稳定后的数据作为后期处理的原始数据。每个数据样本包含5 000个样本点,5类数据共获得637×5=3 138个样本。
考虑到齿轮箱振动频率复杂,因此采用经验模态分解[19](empirical mode decomposition,EMD)得到的内涵模态分量(intrinsic mode functions, IMF)统计特征作为样本的初步特征。特征生成步骤如图8所示。

图8 EMD获取时域统计特征Fig.8 Time domain feature through EMD
对不同健康状态下的数据样本xp利用EMD分解,得到个数为Np的IMF分量IMFp={c1,c2,…,cNp}。考虑到不同样本分解数量的不同,选用所有样本前Nmin个IMF分量作为EMD分解结果,其中Nmin=min{N1,N2,…,Np}。根据下式计算截取IMF分量的能量占原有信号能量的比例。
(6)
计算结果显示,前5个IMF分量样本的能量占比达到93%以上,基本满足特征提取的要求。图9是正常齿轮前6阶IMF的时域图。
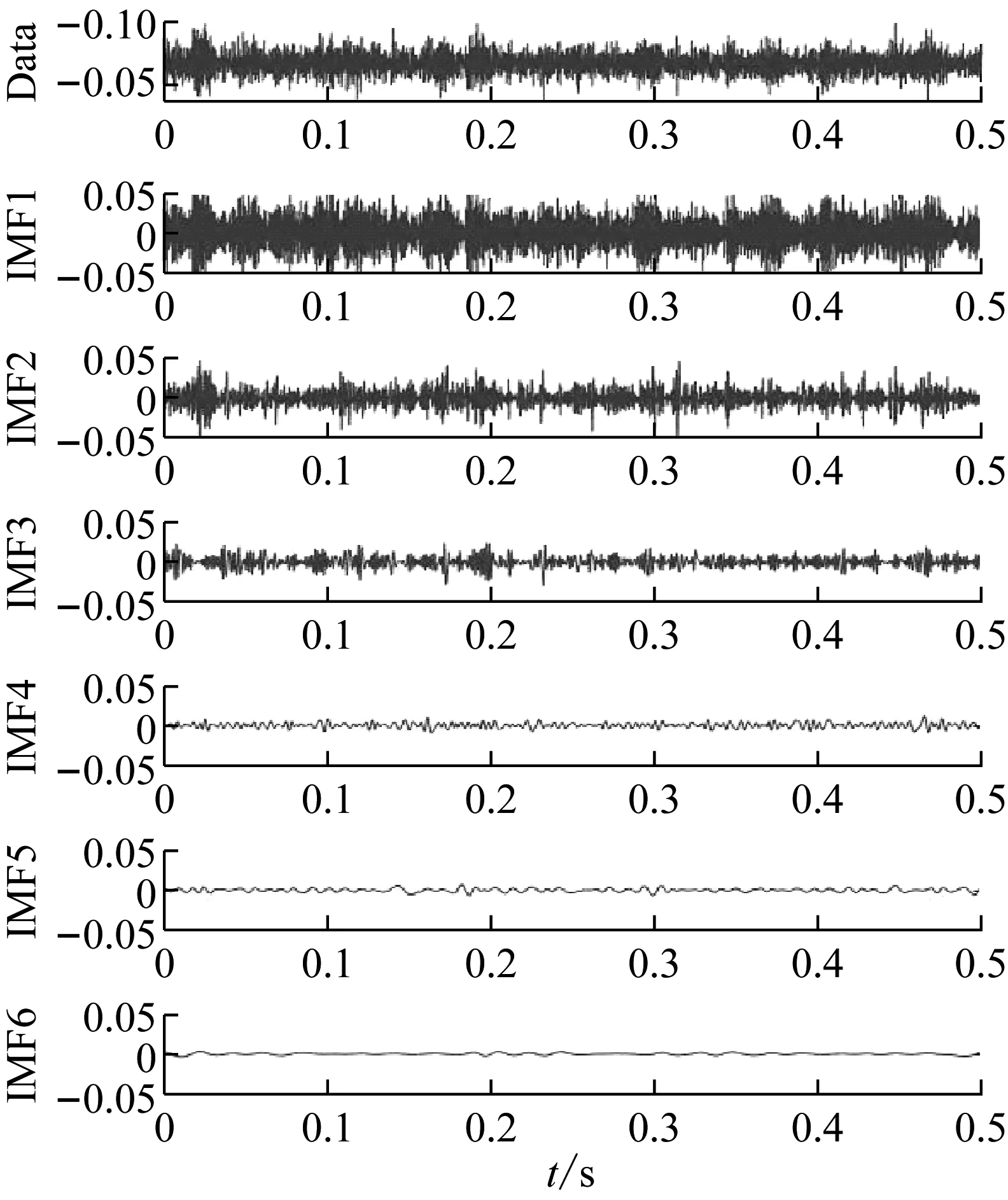
图9 正常齿轮IMF时域图Fig.9 Time domain diagram of IMF ofnormal gear
对提取的IMF分量分别计算时域统计特征,包括均值,峰峰值,峭度等20维时域特征[20]。具体计算方法如表2所示。
5个IMF分量时域统计结果共20×5=100维向量,与原始信号的20维时域统计特征拼接,将其进行Min-Max 归一化获得120维初始向量。
(7)
2.3 错误标签样本生成
实际工程中,错误标签产生的情况较为复杂,难以重现真实错误标签产生过程,因此本文基于齿轮类别间距离生成错误标签数据集。
实际错误标签分两种情况:一种是随机标签,错误标签的生成过程是完全随机的;另外一种是类别相关的错误标签,错误标签和真实标签有一定相关性,如磨损程度所导致的错误标签。本文根据类别间中心距离进行错误标签的设计。对于采集得到的5个类别数据集,选定错误标签比例η,则样本数量为nk的数据集中错误标签样本总个数Nnl为
Nnl=nk×η
(8)
为了构建类相关的错误标签样本,采用类别中心之间欧拉距离D(i,j)作为衡量相关性的指标。
(9)

(10)


图10 基于类间中心距的错误标签样本生成方法Fig.10 Noise label generation methodbased on center distance
2.4 堆栈自编码提取正确样本
堆栈自编码的输入是人工生成,具有同样标签的样本,如图10中的有噪类别1。在循环过程中,通过iForest对样本进行分类,获得正确样本,从而提高自编码对该类样本的关注度。在训练结束后,同样使用iForest挑选错误标签比例低的一部分样本,作为后续交叉验证第一轮的训练样本。堆栈自编码具体参数如表3所示。

表3 堆栈自编码参数
iForest在异常点检测时,需要设置阈值以筛选出错误标签数据。综合考虑后,本文将初始正常点比例设置为0.8,之后基于前后两次正确样本的平均方差σ(x)更新错误标签比例。
(11)
式中,x(i)是数据集样本的第i个特征。
错误标签比例更新方法如图11所示,具体方法如表4所示。

图11 错误标签比例估计方法Fig.11 Method of estimating noise label ratio
改进堆栈自编码是为了获得一部分具有较低错误标签率的样本,因此利用正确样本的个数与伪标签为“正确”样本个数的比值,即精确度作为改进堆栈自编码效果好坏的衡量标准。基于表5所示混淆矩阵,精确度计算方法如式(12)所示。

表4 错误标签比例更新方法

表5 混淆矩阵
(12)
依次将前述生成的5类含有错误标签的样本集作为堆栈自编码的输入数据集,通过iForest对样本进行分类。对比在不同错误标签比例(0.1,0.2,0.3,0.4)下,方法的分类精确度以及错误标签比例的估计情况。
以初始错误标签比例0.3为例,图12(a)为五类齿轮数据经过堆栈自编码和iForest后,分类精确率的变化,12(b)为基于样本平均偏差的错误标签比例变化。

(a) 分类精确度
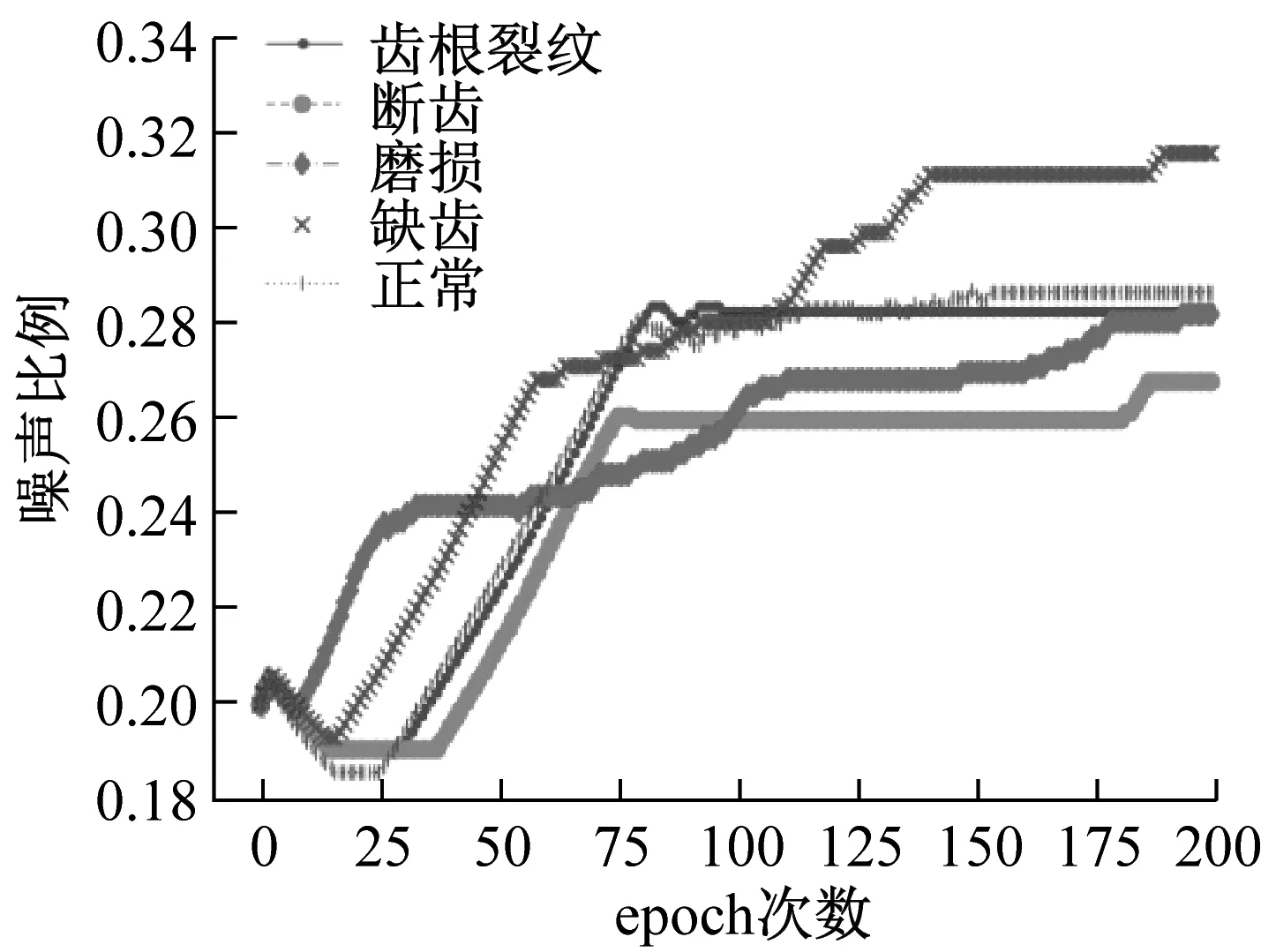
(b) 预测错误标签比例图12 错误标签比例为0.3时分类精确度和预测错误标签比例的训练情况Fig.12 Training process of classification precision and predicted noise label ratio when noise label radio is 0.3
图12(a)表示,随着迭代次数的增加,分类的精确度从最开始的0.7先快速上升至0.8,之后缓慢上升并逐步稳定。正常齿轮数据集的最高精确度可以达到0.95,最终稳定在0.9附近;磨损齿轮数据集精确度最低,稳定在0.8以上。图12(b)表明,随着训练次数的增加,错误标签比例朝向实际比例的方向移动,预测的五类齿轮错误标签比例均落入[0.26,0.32]的区间。综合来看,随着循环次数的增多,改进堆栈自编码的分类精确度在不断上升并稳定,错误标签比例估计也趋于真实情况。
对堆栈自编码获得的特征使用PCA[21],t-SNE[22]两种方法实现可视化,如图13所示。


(a) t-SNE
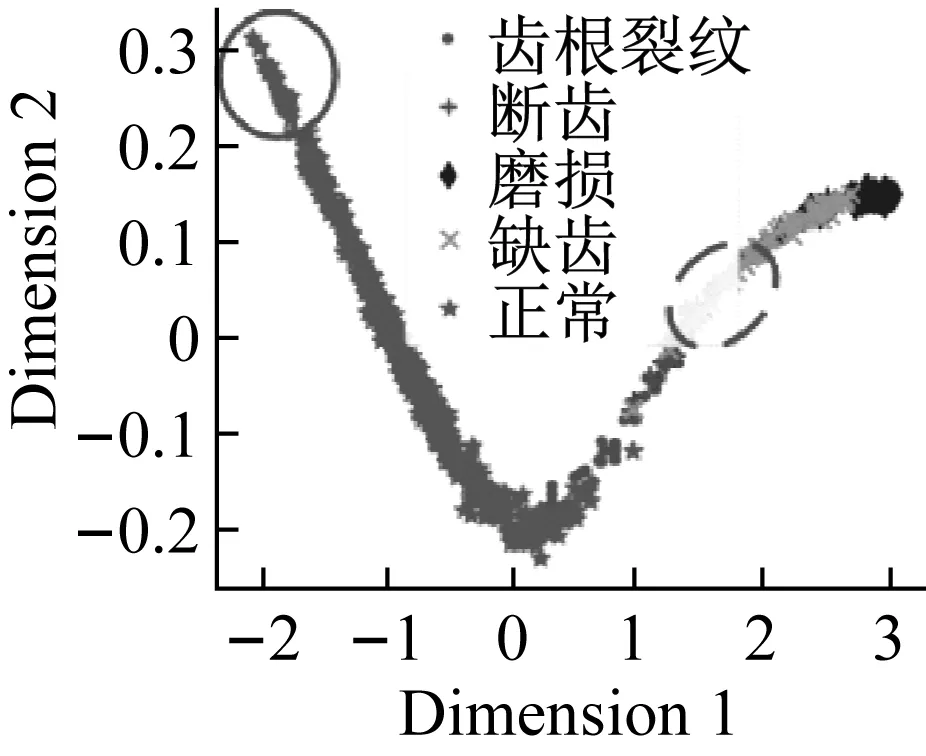

(b) PCA图13 特征可视化和分类结果Fig.13 Visualization of feature and classificationresults
可视化结果表明经过改进堆栈自编码后,正确标签样本与错误标签样本的特征具有一定可区分度。虚线内的样本,错误标签样本被赋予了“正确”的伪标签,实线内的样本,正确标签样本被赋予了“错误”的伪标签。此类情况的出现,降低了分类样本的精确率,后续基于信息熵的标签修正会改善这一情况。
对于错误标签比例η为0.1,0.2,0.4的样本,经过200 epoch后的精确度及预测错误标签比例结果如表6所示。

表6 精确度及错误标签比例结果
在不同的比例下,上述5类含噪样本经过改进堆栈自编码提取样本后,分类精确度受到比例影响,但均有所提高,且能够实现初步的错误标签比例估算。
2.5 基于熵的错误标签修正
利用五类齿轮数据分别训练改进的堆栈自编码网络,得到5个自编码网络。对于每个样本,将五个自编码器生成的结果进行拼接,得到10×5=50维特征,作为交叉验证中的输入特征。
经过30轮交叉验证,错误标签比例η=0.3的样本在不同信息熵阈值β下的错误标签率变化如图14所示。
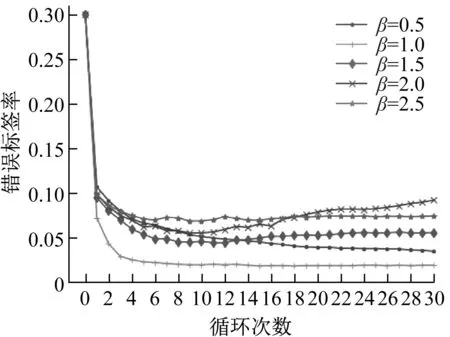
图14 不同阈值下错误标签比例变化Fig.14 Noise label ratiounder different thresholds
由图14可知,经过信息熵的标签修正后,错误标签率均下降明显,可以接近2.5%的错误标签率。具体来讲,在前几轮交叉验证中,错误标签比例有明显下降,后期错误标签比例的变化情况与阈值有关。当熵阈值较小时,比例会随着循环次数逐渐下降,下降速率与阈值大小有关,如β=1与β=0.5的对比。当熵阈值较高时,后期错误标签比例有上升趋势,如β=2的情况。因此信息熵的阈值需要根据样本种类个数进行设置,过高易增加不确定性因素,过低的阈值会降低标签更新速率。
对于η为0.1,0.2,0.4的样本,错误标签比例下降情况如表7所示。
可以发现,其他比例下,信息熵阈值所带来的结果相类似。在信息熵阈值较小时,改进效果明显;信息熵阈值变大后,精确率会有所下降。
综合改进堆栈自编码和基于熵的错误标签修正两个步骤,不同情况下错误标签比例的变化如图15所示。在不同的初始错误标签比例情况下,本文提出的方法可以使错误标签比例有一个明显的下降。
2.6 模型训练
为了对比错误标签数据对模型的影响程度,使用原始含有错误标签样本的数据集和标签修正后的数据训练分类模型,对比分类的准确度。

表7 错误标签比例变化

图15 错误标签比例与方法的变化关系Fig.15 Variation of noise ratio and method
选择所有样本中80%的样本作为训练数据,20%样本作为测试数据,使用LighGBM,XGBoost,卷积神经网络三种方法作为分类器。卷积神经网络参数如表8所示,另外两种方法均采用默认参数。

表8 卷积神经网络分类器参数
不同错误标签比例下预测精确度如图16所示。
使用错误标签数据训练分类器,分类器精确度均在85%以下,最低分类精确度为70%,可见错误标签样本的存在明显影响了分类器的性能。在错误标签修正后,三种分类器的准确度都有上升,低错误标签比例下的初步分类精度可以达到95%。本文所采用的三种分类器受到错误标签的影响也不同,LightGBM和卷积神经网络分类器的精确度在各种错误标签比例下均有15%以上的下降,而XGBoost的分类精确度下降不明显。

图16 错误标签修正前后分类精确度对比Fig.16 Comparison of classification accuracy before and after noise label correction
3 公共数据集
为了进一步验证本文的方法在样本接近的错误标签数据中的效果,本文选用美国凯斯西储大学(Case Western Reserve University,CWRU)的公开轴承振动数据作为验证数据。试验用轴承的内圈裂纹长度分别为0,7,14,21,28 mm,使用采样频率为12 kHz的轴承驱动端振动数据作为样本。首先基于经验模态分解获取样本特征,选取错误标签比例η=0.3的情况,按照距离挑选其他类别的数据,堆栈自编码网络结构及参数与之前相同。图17,图18分别是样本精确度,错误标签预估比例的变化情况。

图17 样本精确度Fig.17 Precision of samples

图18 错误标签比例预测Fig.18 Predicted noise ratio
对于错误标签比例为0.3的轴承数据,本文的方法能够将平均分类准确度提升17.5%,并保持较小的波动。对比图17和图18可以发现,当错误标签比例预测准确的时候,精确度能够得到较好的提升,如裂纹长度为14 mm时,比例估计为0.3,与实际相符,初步的分类精确度在0.95附近波动,有25%的提升。
4 对比分析
存在错误标签样本集可以当作未知标签情况处理,有研究人员通过聚类获得样本伪标签进而辨别错误标签。将错误标签比例η=0.3的齿根裂纹数据集作为对比数据,在堆栈自编码降维后依次使用KNN,谱聚类,iForest的方法获取样本伪标签以识别错误标签。不同方法获得的样本精确度如图19所示。

图19 分类精确度对比Fig.19 Comparison of classification accuracy
相比于本文的方法,使用聚类获得伪标签进而判断错误标签的方法在齿根裂纹数据集中的精确度只能达到80%,谱聚类的方法几乎没有带来精确度的提升。本文改变堆栈自编码对不同样本的重视程度,进一步提高了样本之间的区别,相对于无权重的情况,精确度有8%的提升。
5 结 论
实际问题中,错误标签的出现会使得分类模型产生较差的结果,针对此问题,本文提出了改进堆栈自编码的方法,在错误样本标签修正的问题上进行了探索性的研究。对于存在错误标签的样本集,使用堆栈编码器进行特征的提取以及正确样本的筛选,利用孤立森林获取伪标签,从而使堆栈编码器注重于正确样本。为了弥补权重可能引起的数据偏差,利用基于随机森林的k折验证获取样本的信息熵,通过阈值修正错误的标签。试验表明,本文提出的方法在多个错误标签比例下能够通过修正错误标签来降低样本错误标签率,提高分类器的分类准确度。
本文同时给出了一些简单可行的错误标签数据生成,错误标签比例迭代,以及权重赋予的方法,不同参数更新方法对于整体效果的影响也是进一步探索的工作。
