基于作动器非线性特性的电磁主动悬架混合控制

胡一明 李以农 郑 玲

重庆大学机械传动国家重点实验室，重庆，400030

0 引言

智能电动汽车是当前汽车工业研究中的热点[1]，智能电动汽车高功能集成以及动力学特性智能可控的特点对底盘系统提出了更高的要求。作为智能底盘系统的核心，智能悬架多参数可调、响应快速、节能环保，是实现电动汽车智能化的关键。

电磁主动悬架结构紧凑、配置简单、控制响应快速高效[2-3]，已逐渐取代空气悬架[4]、液压悬架[5]等，成为智能悬架研究中的热点。其中直线式电磁主动悬架克服了旋转式电磁主动悬架传动链长、传递效率损失大、作动力响应迟滞的问题[6-7]，成为目前电磁主动悬架主要的研究方向[8-10]。

目前大部分关于直线式电磁主动悬架的研究都将直线电磁作动器考虑为理想的线性模型[11]，理想作动器模型的作动力与输入电流成正比，忽略了直线电机齿槽结构、端部效应、磁场谐波、磁场饱和等因素导致的电磁力非线性特性。作动器的非线性特性会导致主动悬架控制力输出产生误差，对主动悬架的性能造成一定的影响。

电磁作动器的非线性特性主要包括电磁力的波动问题[12]与电磁力的饱和问题[13]，其中电磁力的波动是指由直线电机齿槽结构、端部效应及磁场谐波等因素导致电磁力在作动器径向不同位置处的幅值不相等，呈现周期性的波动；电磁力的饱和是指由于磁场饱和等因素而导致的电磁力输出存在一个最大值。

目前针对作动器非线性特性对电磁主动悬架控制性能影响的研究相对较少，大部分研究主要着眼于作动器的本体结构，通过合理的结构设计与参数优化来削弱作动器的非线性特性，但作动器的非线性特性是其固有属性，无法被完全消除，因此从作动器结构设计的角度无法完全消除非线性特性对电磁主动悬架控制效果的影响[14]。

综上所述，本文以直线式电磁主动悬架为研究对象，通过直线式作动器结构设计与磁场谐波分析，建立直线作动器的电磁力非线性模型；结合主动悬架，建立电磁主动悬架非线性动力学模型，分析直线作动器非线性特性对主动悬架控制性能的影响；为了消除影响，设计基于滤波递归最小二乘法(FxRLS)自适应补偿的约束H2/H∞鲁棒混合控制器，控制器能对主动悬架控制力进行补偿，使实际控制力接近理想控制力，从而消除作动器非线性特性对主动悬架性能的影响。

1 非线性电磁主动悬架动力学模型

1.1 电磁作动器模型

图1所示为直线式电磁主动悬架典型结构，作动器初级铁心(定子)与轮轴、轮毂、电机和轮胎等簧下质量相连，次级铁心(动子)与车架等簧上质量相连。

图1 电磁主动悬架结构Fig.1 Structure of electromagnetic active suspension

本文直线永磁式作动器采用12槽14极分数槽设计，其中三相绕组采用双层布置。作动器结构如图2所示，作动器尺寸如表1所示。

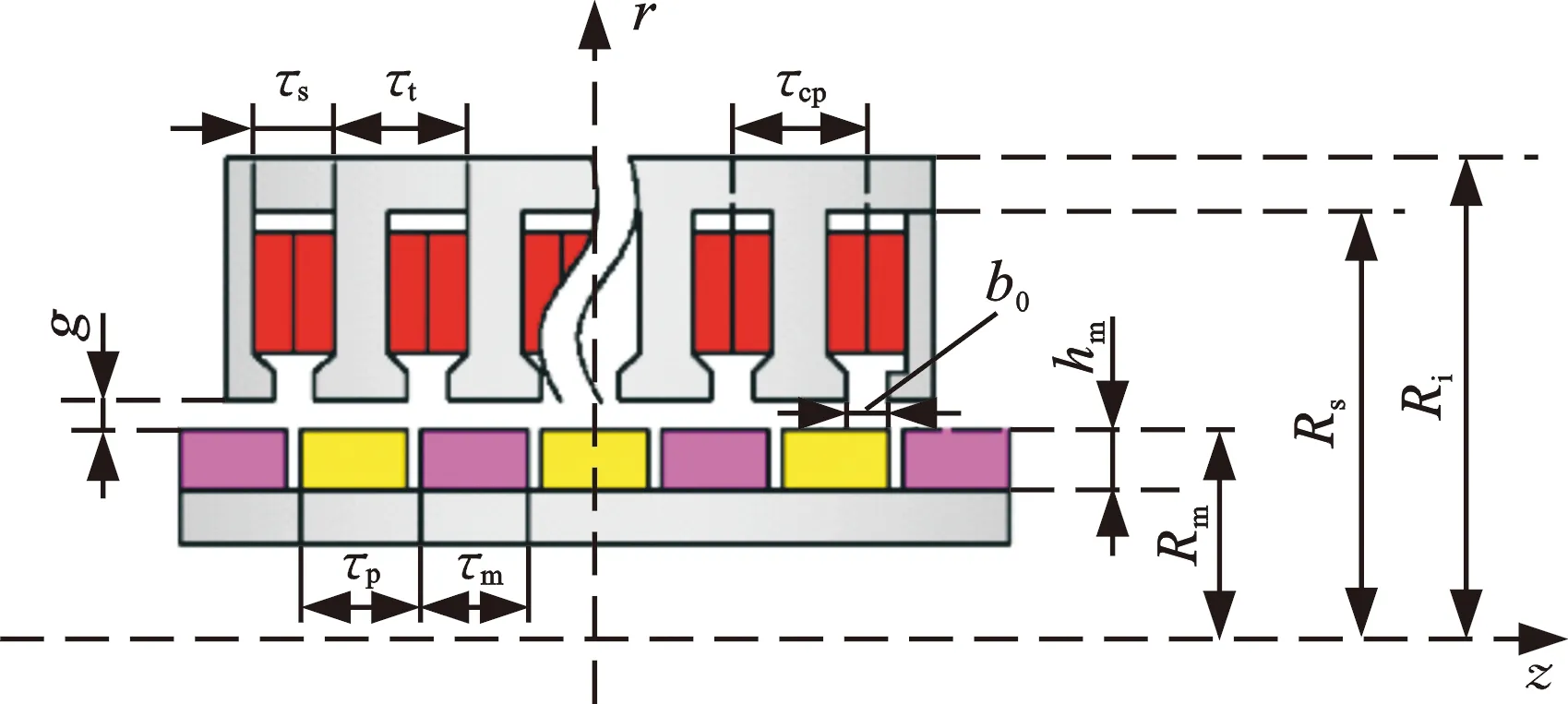
图2 直线式作动器结构Fig.2 Structure of linear actuator

1.2 电磁力波动特性解析

为分析直线式作动器的非线性特性，建立作

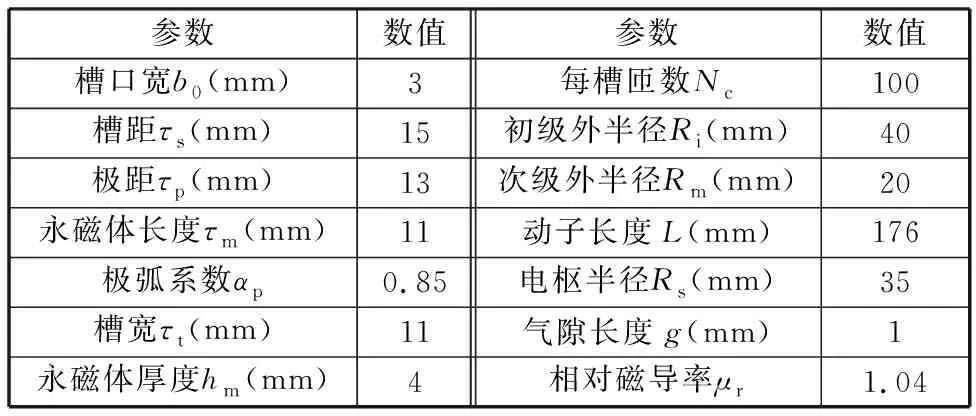
表1 作动器结构参数

动器感应电动势理论计算模型。对于图2所示的直线式作动器，其气隙绕组的感应电动势可以表示为[15]

(1)

式中，E为感应电动势；Ψ为绕组磁链；v为作动器定子与动子的相对速度；p为直线电机极对数；Kdpn为绕组系数；Krn为气隙磁场分布系数；n为谐波阶次；mn为磁链的角频率；z为定子与动子的相对位移；τcp为绕组线圈的节距。

绕组系数可表示为

(2)

气隙磁场分布系数可表示为

Krn=Rse[aInI1(mnRse)+bInK1(mnRse)]

(3)

式中，aIn、bIn分别为第一类贝塞尔函数的系数，与直线作动器的极弧系数和有效电枢半径有关；I1、K1分别为1阶修正贝塞尔一类和二类函数。

有效电枢半径Rse可表示为

Rse=Rm+ge

(4)

其中，ge为有效气隙长度，可表示为

ge=g+(Kc-1)g′

(5)

(6)

(7)

(8)

式中，Kc为卡特系数；g′为考虑齿槽效应的气隙长度；γ为齿槽系数。

根据机电能量转换原理，当绕组导通输入电流时，作动器的电磁力可以表示为

(9)

式中，P为作动器输入总功率；EA、EB、EC为各相感应电动势；IA、IB、IC为各相电流。

三相交流电可表示为

IA=IAmaxsin(ωt-2π/3+φ)

(10)

IB=IBmaxsin(ωt+φ)

(11)

IC=ICmaxsin(ωt+2π/3+φ)

(12)

式中，IAmax、IBmax、ICmax为各相电流峰值；ω为电流角频率；φ为初始相位角，与感应电动势初相位一致。

根据式(9)设定工况速度为0.24 m/s，输入电流为1 A，定子与动子相对位移Δs范围为0～150 mm。作动器的电磁力输出与相对位移的关系如图3所示，可以看出作动器电磁力输出并非恒定值，与定子动子的相对位移呈周期性的波动关系，最大值113.0 N，最小值105.2 N，波动量为7.8 N，电磁力的波动使作动器实际输出与理论值有一定的误差。

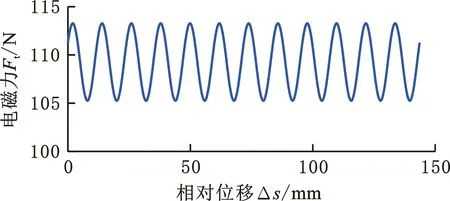
图3 作动器电磁力与相对位移关系Fig.3 The relationship between the electromagnetic force of the actuator and the relative position

1.3 电磁力饱和特性解析

为了分析作动器电磁力的饱和特性，采用Ansoft Maxwell软件建立图4所示的作动器有限元模型，作动器动子和定子铁心采用冷轧硅钢片叠制而成，型号为DW465_50；永磁体为钕铁硼N30，矫顽力838 kA/m，剩余磁密1.1 T，采用径向充磁，绕组为铜线，直径为1 mm，气隙空间设置为真空。在作动器运动的区域外施加Balloon气球边界。由于本文作动器为对称结构，故模型关于Z轴旋转对称。

图4 作动器有限元模型及网格划分Fig.4 Finite element model and meshing of the actuator

当定子动子相对位移不变时，接通外部电流，分析不同输入电流时作动器电磁力的输出，结果如图5所示，图中包含了理论计算结果以及有限元仿真结果。

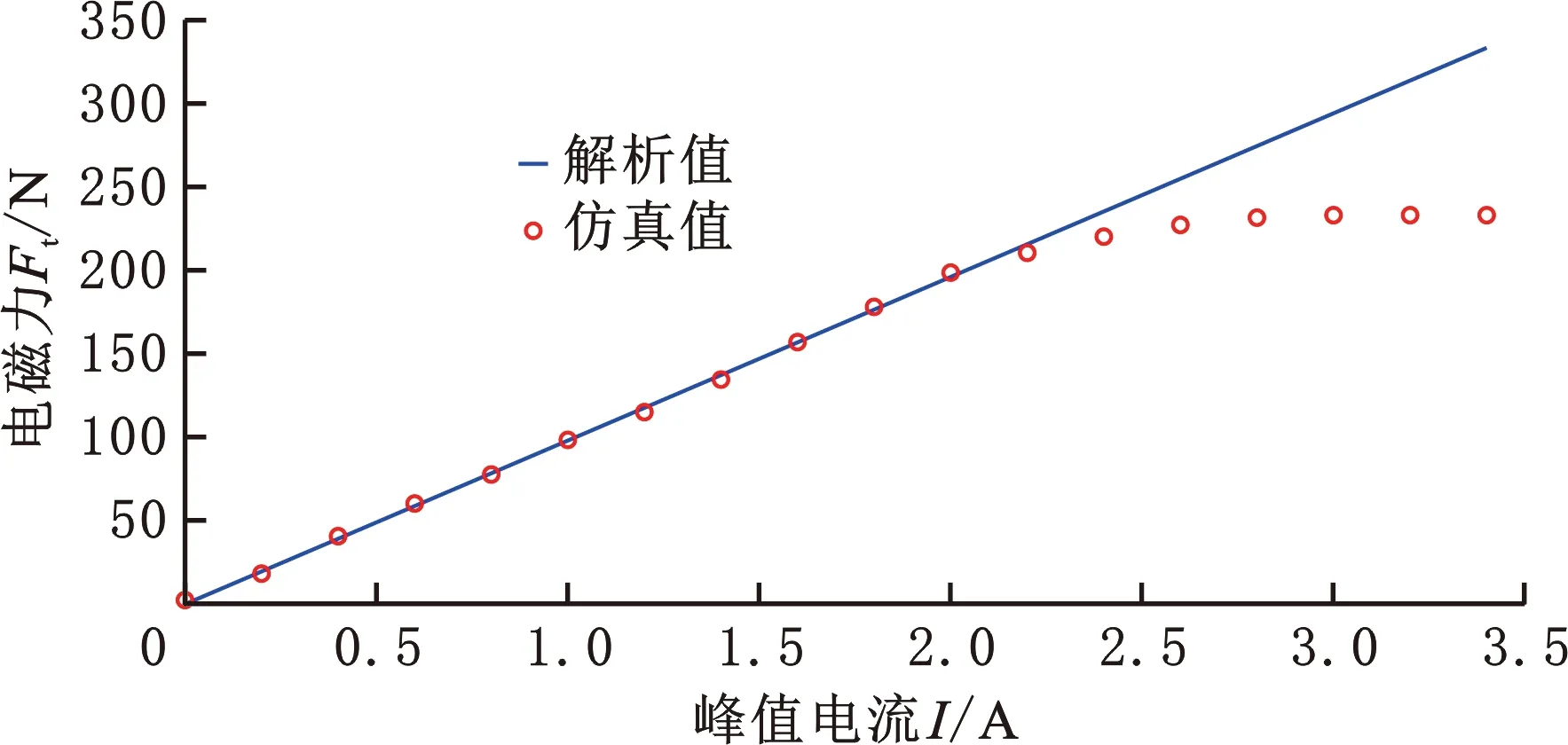
图5 作动器电磁力与电流关系Fig.5 The relationship between electromagnetic force and current of actuator

从图5中可以看出，理论计算的电磁作动力呈线性增长，斜率约为98 N/A。大多数文献对该电磁作动力的计算均默认为电流的线性函数，而受作动器磁场饱和及温升效应的影响，实际电磁力并非稳定地线性增长，电磁力在电流幅值为0～2 A时基本呈现线性增加，斜率与理论计算一致，2～2.8 A时电磁作动力增长逐渐趋于平缓，当电流大于2.8 A时电磁作动力稳定于233 N。

如上所述，可以看出直线式作动器的非线性特性主要包括两个方面，即由磁场谐波导致的电磁力波动现象以及磁路饱和导致的电磁力饱和现象。

1.4 考虑作动器非线性输出的主动悬架模型

以四分之一车辆动力学模型为基础，结合电磁力解析模型与有限元模型，建立考虑作动器非线性电磁力输出的电磁主动悬架仿真模型。图6为非线性模型的总体结构图，其中主动控制器为广泛采用的LQR控制器，作动器输出基于前述的电磁力波动解析模型。图中，Ms、Mu分别为簧载质量和非簧载质量；Ks、Cs分别为悬架的刚度和阻尼；Kt为轮胎刚度；Zs、Zu、Zg分别为簧载质量的位移、非簧载的质量位移以及路面不平度激励；Fa为主动控制力，Ke为电机常数[16]。

图6 考虑非线性电磁力的主动悬架动力学模型Fig.6 Dynamic Model of Active Suspension Considering Nonlinear Electromagnetic Force

系统耦合逻辑如下：控制器根据需求的理论控制力得到理想输入电流，作动器输出模型根据系统运行状态(定子动子相对速度、定子动子相对位移)得到包含波动项的实际输出控制力，根据有限元分析结果，将电流峰值限制为2.8 A以模拟磁路饱和，最后，将实际输出的控制力Fa加载于系统得到车辆动力学响应。模型的结构参数如表2所示。

表2 车辆结构参数

2 电磁主动悬架混合控制

目前广泛采用的主动悬架控制算法如LQR控制、鲁棒控制等大多是基于线性的控制力输出，而作动器非线性输出会降低系统的控制性能，破坏控制器的平衡。本文采用自适应滤波反馈控制与鲁棒前馈控制结合的混合控制器来缓解作动器非线性特性对主动悬架性能影响。通过约束H2/H∞鲁棒前馈控制器得到车辆所需的理论控制力，并通过FxRLS自适应滤波反馈控制器对输入电流进行补偿以消除电磁力输出波动。

2.1 FxRLS自适应控制力补偿

当作动器存在非线性特性时，实际输出电磁力与理论输出电磁力不相等，本文以FxRLS自适应滤波器作为反馈控制器，根据车辆的工作状态对实际输入电流进行补偿以达到减小控制力输出误差的目的。根据文献[17-18]拟定自适应滤波器迭代控制算法如下：

(13)

MQ×m×k=

滤波器的电流输出为

(14)

当滤波权重W迭代收敛时，滤波器能对实际输入的控制电流Iq进行补偿，从而对作动器实际输出的控制力进行补偿，使其接近理想控制力Fa。

2.2 多目标粒子群约束鲁棒控制器

鲁棒控制器用来计算所需的理论控制力，且保证一定峰值力约束下的性能最优，根据文献[19-21]，本文采用约束H2/H∞鲁棒控制器。

将车辆动力学方程表示成如下约束形式的状态方程：

(15)

式中，A、B1、B2、C1、D11、D12、C2、D21、D22为系统的参数矩阵；z2i，max为H2性能指标最大允许输出；ui，max为最大允许控制力输出。

选择簧载质量振动加速度作为H2性能指标，选择悬架动挠度和车轮跳动量作为H∞性能指标，则状态变量与系统输出变量分别为

Z2=[Zu-ZsZg-Zu]T

(16)

S=A+B2K

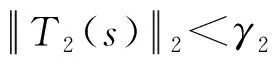
(17)

(18)

(19)

(3)系统约束成立的条件为，对于给定的常数α，当且仅当存在一个对称的正定矩阵U以及Z，使得：

(20)

(21)

(22)

(23)

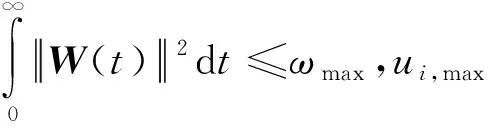
2.3 控制器反馈矩阵的求解

约束H2/H∞鲁棒控制律求解可以描述为如下的多目标寻优问题：

(24)

L={x∈Rn，G：gi，min≤gi(x)≤gi，max，

i=1，2，，…，u}

(25)

式中，L为变量设计约束；Rn为设计变量域；G为变量约束。

如上所述，可利用多目标粒子群算法(MOPSO)对控制律K进行搜索，使得γinf与γ2最小，优化变量取控制律K与参数α。参数α仅能保证理论上的性能约束，且难以选取，会造成控制律K搜索的保守性，本文在多目标优化过程中加入时域约束判定，通过多目标粒子群算法的特殊性，用任意搜索的解对系统进行动力学仿真，如果解不满足最大控制力要求，则排除此解，使得优化结果满足约束条件。多目标粒子群算法流程如图7所示。

图7 多目标粒子群计算流程图Fig.7 Flow chart of MOPSO

图8为寻优结果的Pareto前沿可视图，Pareto解集中共有430个解，各个解之间均满足Pareto非支配关系。Pareto解为一系列非支配解，需要从解集中选取典型解作为控制器的控制律，为了排除解选取中的人为因素，采用模糊集理论对Pareto解进行选优[22]。

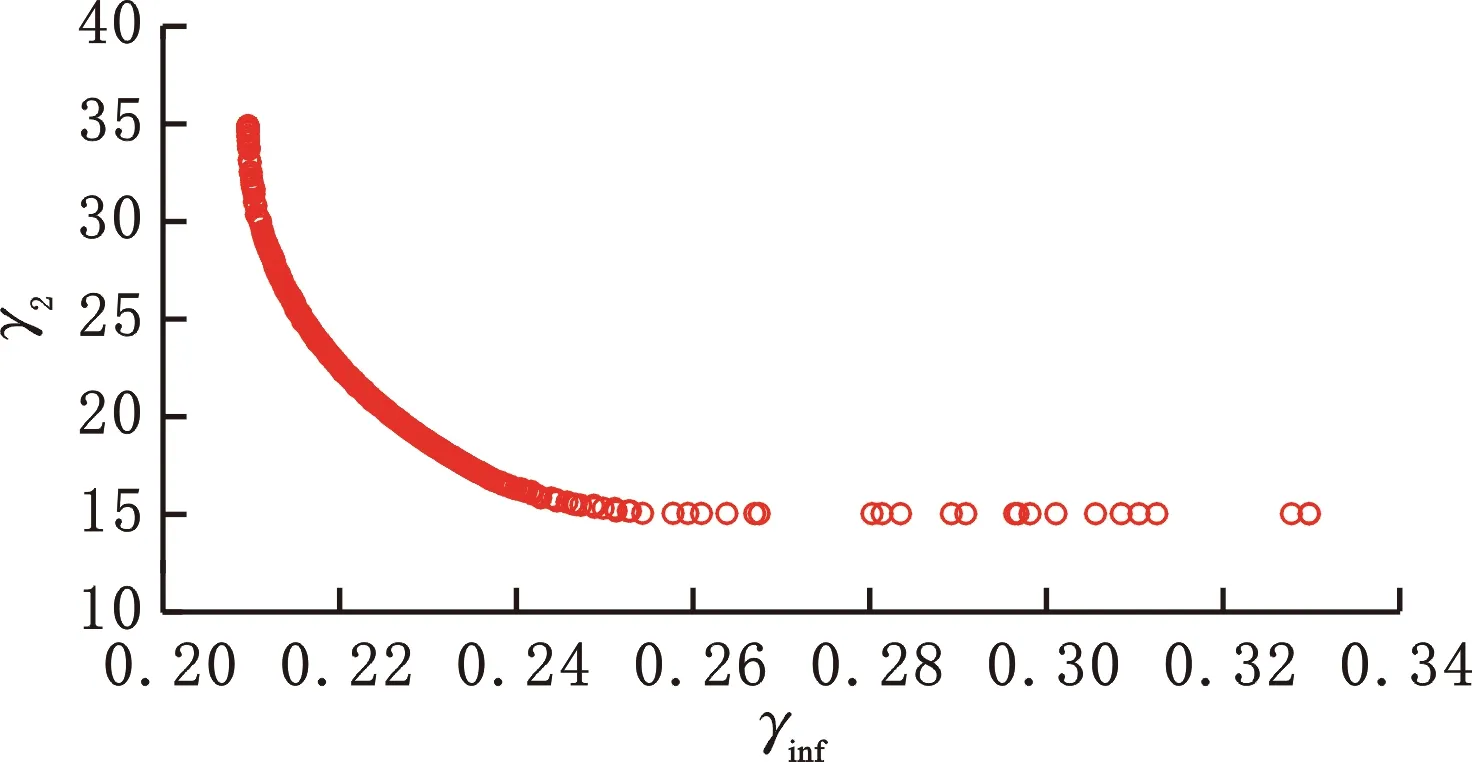
图8 Pareto前沿可视图Fig.8 Pareto front

定义隶属函数：

(26)

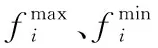
定义支配函数φk，第k个解的支配值为

(27)

式中，l为外部集中解的数目；n为悬架优化设计目标个数。

根据模型的仿真结果，l=430，n=2。图9所示为解集中各解的支配值，其中最大支配值为第330号解，将此解作为鲁棒控制器的控制律。

图9 外部集中各解的支配值Fig.9 Dominant value of each solution in external set

将上述所设计自适应补偿控制器以及约束H2/H∞鲁棒控制器串联，得到图10所示的混合控制器。混合控制器控制逻辑为：H2/H∞鲁棒前馈控制器通过系统状态估计得到当前系统所需的理论控制力，基于线性电机常数得到理论输入电流，通过理想的控制输入得到此时车辆的理想系统响应估计；基于理想的系统响应与实际系统响应的误差，采用FxRLS自适应滤波算法对理想输入电流进行补偿得到实际输入电流，从而得到实际控制力输出。FxRLS自适应滤波反馈控制器的作用在于使系统的实际响应与理论响应一致，当两者一致时即说明控制力输出与理论控制力输出一致。

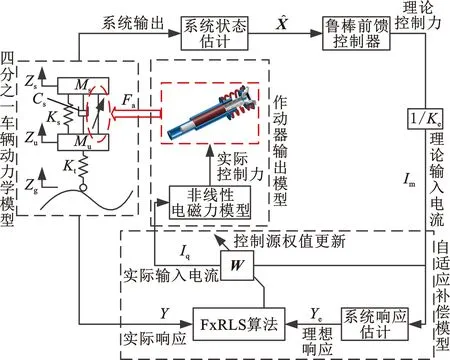
图10 混合控制器控制逻辑Fig.10 Control logic of hybird controller

3 结果分析

根据上述介绍对基于LQR控制器与混合控制器的非线性动力学模型进行仿真对比分析，自适应滤波控制器阶数为24，仿真工况为B级路面，车速为72 km/h。

3.1 考虑作动器非线性的输出特性分析

图11为作动器电磁力输出特性图，表3所示为作动器输出值对比。可以看出基于LQR控制器的主动悬架实际控制力输出与理论值有明显的差距。较大的控制力输出峰值由于磁场饱和效应难以达到，而较小的控制力输出也存在可见的波动误差。由图11b的频域对比可看出，实际控制力输出能量在车辆的一阶自然频率和二阶自然频率附近均有明显降低，根据统计结果，实际输出控制力的均方根值由207.9 N降低至146.3 N，峰值由591.2 N降低至252.9 N，实际输出与理论输出之间的差值最大达到404.7 N，均方根值达到83.9 N，这种作动器实际输出的误差与不足可能导致控制器性能的降低或控制目标之间的失衡。由图11c可以看出，基于混合控制的电磁主动悬架实际输出控制力与理论控制力比较接近，实际控制力与理论控制力的均方根值分别为95.6 N、87.0 N，控制器的输出误差较小，控制力峰值分别为250.9 N、224.9 N，作动器的输出基本覆盖了理论控制力的需求范围。但如表3所示，控制力输出与控制效率的降低是否会影响控制器性能有待进一步分析。

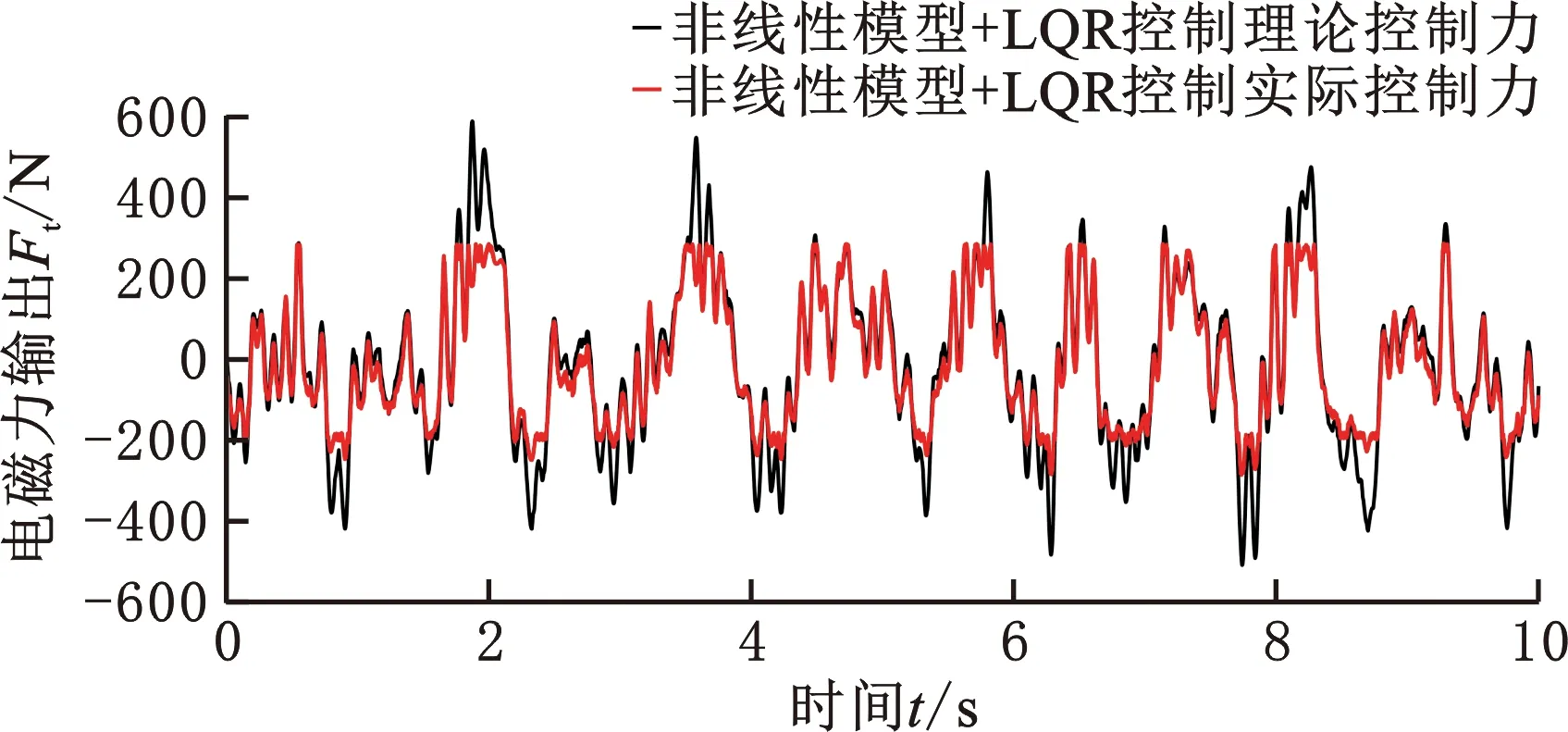
(a) LQR控制控制力输出对比

表3 作动器输出统计结果

3.2 系统响应特性分析

图12为车辆的时域响应对比图，图13为时域响应的功率谱密度图，表4所示为系统响应的均方根值统计对比。

(a) 簧载质量振动加速度

如图12a、图13a所示，当考虑作动器非线性特性时，车辆在一阶自然频率附近出现了性能恶化，其时域响应峰均有一定的增大，根据前述分析，可推测作动器的非线性特性导致的输出误差使主动悬架在舒适性控制目标上存在一定的性能恶化。基于混合控制的主动悬架改善了低频处的控制器性能，均方根值由0.99 m/s2降低至0.96 m/s2，基本消除了作动器非线性特性对舒适性的影响。从频域上看，一阶自然频率与二阶自然频率附近的振动能量都有明显的降低。

(a) 簧载质量振动加速度

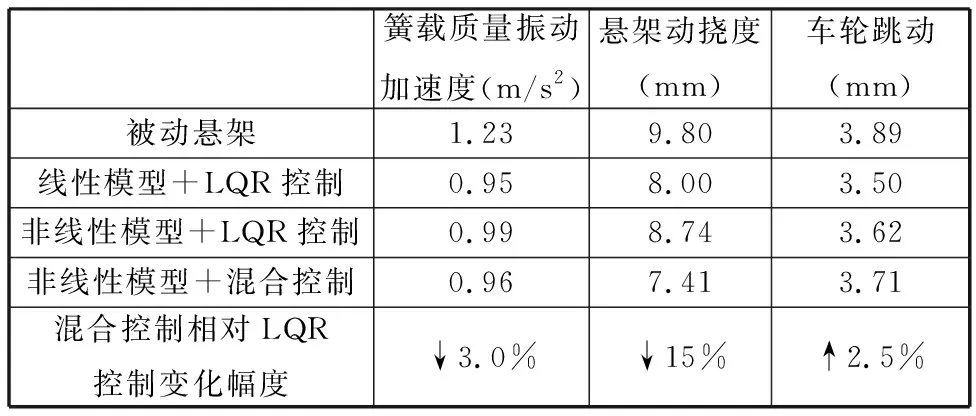
表4 系统响应统计结果

由图12b、图13b可以看出，作动器非线性特性对悬架动挠度的影响较大，时域响应输出升高明显，从功率谱密度图上看，一阶自然频率附近振动能量显著增大，二阶之后的高频振动能量也有一定的增大，其均方根值由8.0 mm升高至8.74 mm，性能恶化9.1%。混合控制器能在保证高频振动能量不恶化的情况下，优化主动悬架一阶自然频率附近的响应，均方根值由8.74 mm降低至7.41 mm，性能提高15%，大幅优化了车辆的姿态控制能力。

从图12c、图13c中可以看出，车轮跳动对作动器非线性特性不敏感，其时域响应仅有小幅升高，频域上变化也不大。而基于混合控制器的系统在车轮跳动量上甚至有小幅升高，均方根值由3.62 mm上升至3.71 mm，性能小幅恶化2.5%，这是由于主动控制力减小导致，控制能量的减少势必会牺牲某一方面的性能，由于仿真车速较低，轮胎接地性能的略微降低处于可以接受的范围，对行驶安全性的影响较小。

总地来说，作动器的非线性特性会导致主动悬架电磁控制力的输出产生一定的误差，使得主动悬架控制性能降低，并且打破原主动悬架控制目标之间的平衡。而混合控制器以极小的代价消除了作动器非线性特性对控制性能的影响，使得作动器长期工作在非饱和区间，降低了作动器的能量消耗，既提高了作动器硬件的工作稳定性及耐久性，又使控制器理论设计与实际工作特性匹配程度更高。

4 结论

本文针对直线作动器非线性特性导致的电磁主动悬架性能降低问题，采用理论分析与仿真分析相结合的方法，建立了考虑作动器非线性特性的电磁主动悬架动力学模型。研究了非线性特性对主动悬架控制性能的影响，提出了基于FxRLS自适应滤波补偿与多目标粒子群约束H2/H∞鲁棒控制结合的混合控制方法，得到的结论如下：

(1)主动悬架电磁作动器的非线性特性主要包括磁场饱和导致的作动力输出不足以及电磁力波动导致的控制力输出误差。对于传统主动悬架控制器，其控制力不足最大可达404.7 N，波动量的均方根值可达83.9 N，导致悬架控制性能有一定程度的降低，控制器理论设计与实际工作特性不匹配，作动器非线性特性使得簧载质量振动加速度、悬架动挠度以及车轮跳动量分别降低4.0%、9.1%、3.5%。

(2)FxRLS自适应滤波补偿与约束H2/H∞鲁棒前馈控制器相结合的混合控制器，在控制器理论设计阶段就将实际控制力约束于作动器工作的非饱和区间，且能对电磁力的波动进行自适应的补偿，有效地降低了作动器非线性特性对电磁主动悬架性能的影响，提高了作动器的工作稳定性及耐久性，降低了主动悬架控制器理论设计与实际工作情况的不匹配度。