航发叶盘类零件不同抛磨工艺的仿真对比分析*

闫泽昭,李文辉,李秀红,张 演

(太原理工大学 a.机械与运载工程学院;b.航空航天学院;c.精密加工山西省重点实验室,太原 030024)

0 引言

随着航空、运输、通讯、军事等领域的快速发展，高端设备上的高性能零件数量与日俱增[1]。相较于普通零件，这种高性能零件不仅对表面尺寸精度要求高，而且朝着高性能指标、难加工材料和精细复杂表面发展[2]，因此迫切需要能够满足高性能零件要求的精密加工方法。

整体叶盘是航空发动机上的核心零部件，对提升发动机性能、降低重量、提高推重比起到重要作用[3]。整体叶盘空间扭曲复杂、加工可达性差，且大多采用难加工的先进复合材料[4]，这些因素对整体叶盘的加工提出巨大挑战，直接制约着下一代航空发动机的发展。整体叶盘服役环境恶劣，必须克服极强的热负荷和振动负荷，对加工精度和表面质量要求很高[5]。整体叶盘经过近成形和精确成形加工后的表面质量仍无法满足服役要求[4]，需要进一步的加工抛磨来降低表面粗糙度、提高疲劳强度等。整体叶盘抛光工艺有手工打磨、数控抛光、喷丸强化和抛磨加工等，其中手工打磨不仅劳动强度大，而且依赖于工人的经验和熟练度，具有不稳定性[6]；数控抛光程序复杂，相邻叶片间通道狭窄，加工叶根时可能出现干涉现象[7]；喷丸强化可提高表面强度，但同时会增加表面粗糙度[8]。上述加工工艺存在的不足严重影响着整体叶盘的轮廓精度及表面完整性。抛磨加工是一种自由磨具光整加工，通过滚抛磨块与工件之间的相对运动，对工件产生滚压、碰撞、划擦和刻划等微量磨削作用，改善工件表面几何特征，提高表面物理机械性能[9]。作为一种实用型表面加工工艺，抛磨加工与上述工艺相比具有的优势为有较强的零件适应能力、加工质量高、加工环境友善[10]及可批量化生产。

抛磨加工工艺的类型主要有振动式、回转式、离心式、涡流式等[11]，众多学者根据多种评价指标，对抛磨加工进行了深入理论分析和实验验证。田雨[12]首次在抛磨加工中引入EDEM离散元软件，通过实验分析的转速、滚抛磨块装入量及滚抛磨块尺寸对加工效率的影响与仿真结果基本一致，证明了EDEM软件在抛磨加工仿真中的适用性。李鹏等[13]对整体叶盘回转式抛磨加工进行了仿真模拟并计算出滚筒最适宜的理论转速，但是该工艺的加工效果仍无法满足整体叶盘的加工要。本文通过仿真对比分析了回转式和振动式抛磨加工整体叶盘的优缺点，在此基础上提出振动回转式抛磨加工并加以仿真分析。

1 仿真前处理

1.1 模型建立及网格划分

由于整体叶盘的叶片数目较多且型面弯扭复杂，不利于对仿真结果进行定性分析，因此对整体叶盘的模拟件进行保持整体叶盘结构特性的简化处理。表1为简化后的模拟件和滚筒的模型尺寸。通过ANSYS软件对模拟件进行网格大小为1 mm的六面体网格划分，得到msh文件并导入到EDEM软件中，模拟件的网格模型如图1所示。

图1 模拟件网格模型

表1 模型尺寸

1.2 接触模型及材料参数

EDEM中的接触模型有Hertz-Mindlin(no-slip)和Hertz-Mindlin with Archard Wear接触模型等。Hertz-Mindlin(no-slip)接触模型是EDEM默认使用的模型，计算受力方面精确且高效，但不进行磨损统计。Hertz-Mindlin with Archard Wear接触模型基于J F Archard磨损理论，可以近似计算出几何表面磨损深度数值。为防止滚抛磨块生成阶段对整体叶盘的碰撞划擦导致的误差，从滚抛磨块生成到完全静置这个阶段选用Hertz-Mindlin(no-slip)接触模型，加工时使用Hertz-Mindlin with Archard Wear接触模型并进行相关数据统计。

设置滚抛磨块直径为4 mm，装入量为滚筒体积的60%。工件、滚抛磨块及滚筒材料分别为钛合金、氧化铝和尼龙，材料本征参数与接触参数如表2、表3所示[14]。

表2 材料表征参数

表3 仿真接触参数

综合考虑计算精度和仿真速度，将时间步长设为Rayleigh时长的20%，仿真时间为20 s。

1.3 数据提取及评价指标

仿真结束后通过在工件表面覆盖数据块的方法来提取数据，数据块有两种类型，一种是在工件表面覆盖1张数据块，另一种是划分成60个小数据块并覆盖工件表面，如图2所示。为了分析不同区域磨损量的变化，从顶部至根部依次添加10个数据块，在前缘和后缘间依次添加6个数据块，数据块编号见图3，设P1、P10为顶部和根部，F1、F6为前、后缘。

图2 划分数据块 图3 数据块编号

仿真结果的评价指标有模拟件表面磨损量、磨损量变异系数、滚抛磨块速度及滚抛磨块速度的变异系数，变异系数的计算公式为：

RSD=(SD/X)×100%

式中，SD为数据的标准偏差,X是其均值。变异系数能够准确描述数据偏离均值的程度，RSD值越小，表明加工均匀一致性越好[13]。

2 仿真分析

2.1 不同抛磨方式仿真对比

根据李鹏等[13]对回转式抛磨加工整体叶盘的仿真分析可知，回转式加工可以保证整体叶盘不同叶片之间的加工均匀一致性，但从磨损量变异系数及磨损云图来看，回转式加工同一叶片不同区域的均匀一致性较差。

王秀枝等[15]通过对盘类零件回转式、振动式及离心式抛磨加工的仿真分析发现，在一定条件下振动式加工盘类零件的均匀一致性优于回转式及离心式。同时研究发现在振动式抛磨加工中，盘类零件的受力与滚抛磨块在零件表面的速度从中心区域向边缘处逐渐增大，零件表面磨损量变化趋势也以零件中心轴对称，边缘处的磨损量最大。

在上述学者研究的基础上，将振动式抛磨加工引入整体叶盘的表面光整加工中，并对整体叶盘的模拟件进行回转式和振动式抛磨加工仿真。振动式加工有两种方式，第一种是滚筒振动式，模拟件固定不动，滚筒轴向振动；第二种为同步振动式，模拟件和滚筒同步轴向振动。回转式加工在加工周期过半时会进行反转加工，振动式加工则会翻转模拟件进行翻面加工。模拟件和滚筒的放置方式及运动方式如图4所示。

(a)回转式 (b)滚筒振动式 (c)同步振动式

由于模拟件的叶片为直叶片，为了便于分析，对其型面位置及边缘处进行命名。如图5所示为振动式加工中模拟件正面、背面、前缘、后缘、顶部和根部各自的位置，在回转式加工中各位置名称不变。

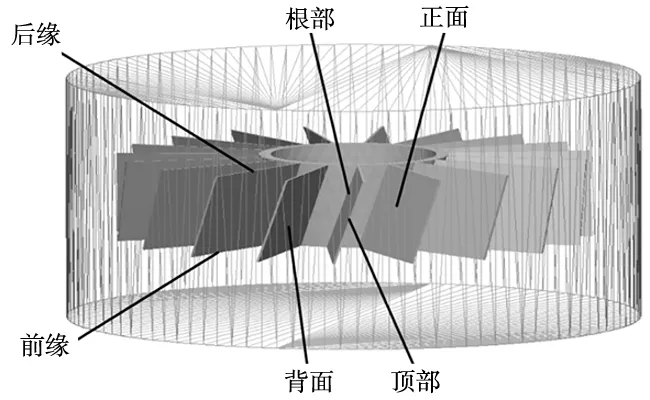
图5 模拟件型面位置

2.1.1 加工效率及均匀一致性分析

设置运动参数：转速N=±60 rpm、振动频率f=40 Hz、振幅A=2 mm。图6为仿真后模拟件表面磨损量及磨损量变异系数。回转式加工正面磨损量为1.431 μm，背面为1.249 μm；滚筒振动式加工正面磨损量为1.284 μm，背面为1.174 μm，同步振动式则是正面7.61 μm，背面7.67 μm。从磨损量变异系数来看，回转式加工后的磨损量变异系数最高，正面为0.785 4，背面为0.759 2；滚筒振动式加工正面磨损量变异系数为0.410 32，背面为0.379 2；同步振动式则是正面为0.346 29，背面为0.314 09。结果显示，不同加工方式的加工效率为同步振动式>回转式>滚筒振动式，加工均匀一致性为同步振动式>滚筒振动式>回转式。

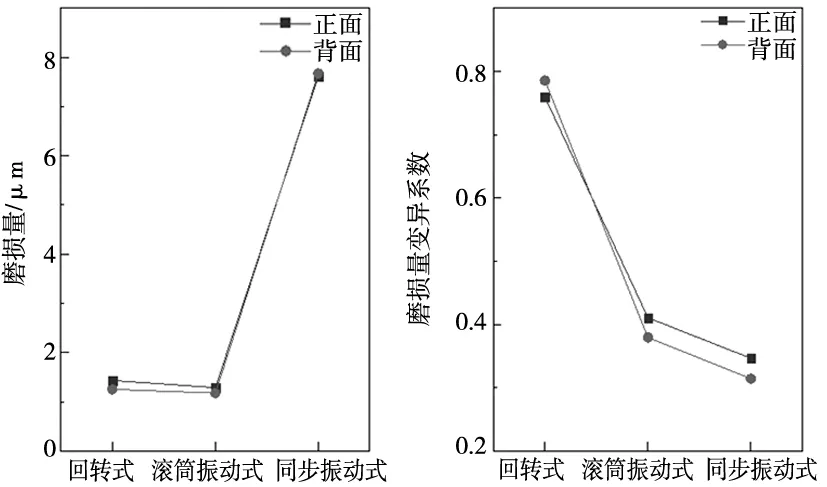
图6不同加工方式下的磨损量及变异系数

图7为不同区域的磨损量。

(a)回转式

由图可见，回转式加工P1处磨损量比P10处高约8.18～8.65倍，滚筒振动式加工高约1.96～2.62倍，同步振动式加工高约1.63～1.77倍。从不同加工方式下F1、F6处与中间区域F2～F5处的磨损量对比来看，回转式加工F1、F6处的磨损量约为中间区域的3.1～5.66倍，滚筒振动式加工后约为2.13～2.81倍，同步振动式加工后约为1.81～2.01倍。回转式、滚筒振动式及同步振动式加工P1处的磨损量都大于P10处，F1～F6方向的磨损量呈先减后增趋势，不同的是回转式、滚筒振动式及同步振动式加工P1处与P10处磨损量差值递减，F1、F6处与中间区域的磨损量差值也依次缩短。

与振动式加工相比，回转式加工效率低，P1处和P10处的磨损量差值大，这是因为回转式加工中滚筒的运动次数较振动式加工少，滚抛磨块在模拟件表面的碰撞滑擦次数较低，并且回转式加工中模拟件表面的滚抛磨块速度与所受离心力有关，其离心力半径为滚抛磨块距P10处的距离，距离越短离心力就越小，因此P1处～P10处的滚抛磨块速度递减，导致磨损量差值较大。与回转式加工相比，振动式加工后的模拟件F1～F6处的磨损量差值较大，这是因为振动式加工存在埋入深度的问题，埋入深度越深磨损量就越高，并且边缘处与滚抛磨块碰撞滑擦的次数较多，因此出现F1～F6处磨损量差值较回转式加工大的现象。根据仿真结果，单一的加工工艺都存在不足之处，经回转式、振动式加工后的模拟件都存在P1处P10处磨损量差值较大的现象，并且F1～F6方向磨损不均匀。

2.1.2 流场行为分析

图8为三种加工方式下滚抛磨块在模拟件表面的速度云图。

(a)回转式加工正面滚抛磨块速度

由图8可知回转式加工中，滚抛磨块的速度从根部到顶部递增，前缘到后缘方向的速度变化不明显。振动式加工下的滚抛磨块速度从前缘到后缘先减后增，顶部到根部方向的速度缓慢增大。同时发现，回转式加工中滚抛磨块的速度大于振动式加工，因此滚抛磨块在回转式加工中的运动较振动式加工剧烈。

图9为模拟件顶、根部及前、后缘滚抛磨块速度。

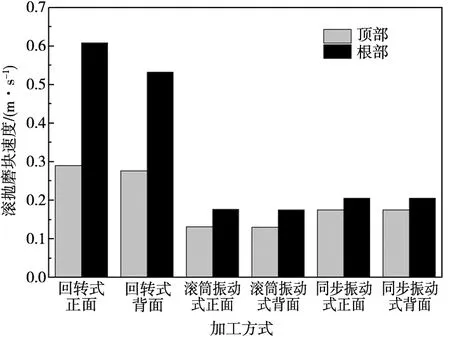
(a)顶、根部滚抛磨块速度

由图可见，相较于振动式加工，回转式加工的优点是前缘至后缘方向滚抛磨块速度差值较小，缺点是顶部至根部方向滚抛磨块速度差值较大，振动式加工则反之。

由上述研究可知回转式加工中滚抛磨块运动较振动式加工剧烈，振动式加工的加工效率及加工均匀一致性较高，为了保证多个面之间的加工均匀一致，同时通过提高滚抛磨块在模拟件表面的接触随机性来提升单个面内的加工均匀一致性，将回转式和振动式组合起来，耦合构建振动回转式加工下的滚抛磨块流场。通过回转的作用降低前后缘表面滚抛磨块速度差值，通过振动的作用降低顶部和根部表面滚抛磨块速度差值，同时提高加工效率。

2.2 振动回转式加工方案

振动回转式加工如图10所示。以滚筒轴线和轴截面的交点为原点O，垂直于轴线水平向右为X轴，垂直于轴线竖直向上为Y轴，滚筒中心线所在方向为Z轴建立空间直角坐标系OXYZ。加工时滚筒和整体叶盘绕Z轴振动，并同步进行往复回转运动。如图11所示为4种方案加工后的磨损量及变异系数。

图10 加工示意图

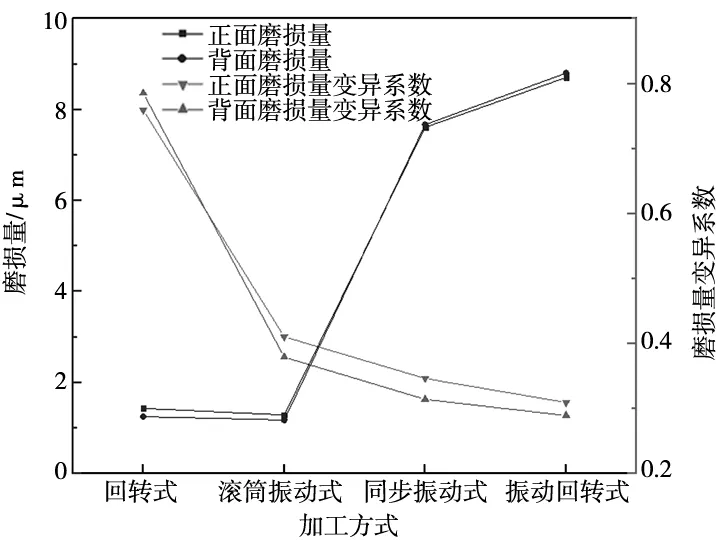
图11 4种加工方式下的磨损量及变异系数

由图可见，振动回转式加工后的磨损量最高，正面和背面磨损量分别为8.707 3 μm和8.805 1 μm，依次为回转式、滚筒振动式及同步振动式的6.08～7.04倍、6.533～6.775倍和1.144～1.147倍。同时可知振动回转式加工的磨损量变异系数最低，正面和背面磨损量变异系数分别为0.309 29和0.289 06，依次为回转式、滚筒振动式及同步振动式的0.367～0.40倍、0.753～0.762倍和0.893～0.920倍。仿真结果显示，相较于回转式和振动式，振动回转式抛磨加工效率高，加工均匀一致性好。

如图12所示为振动回转式加工下的滚抛磨块在模拟件表面的速度云图。

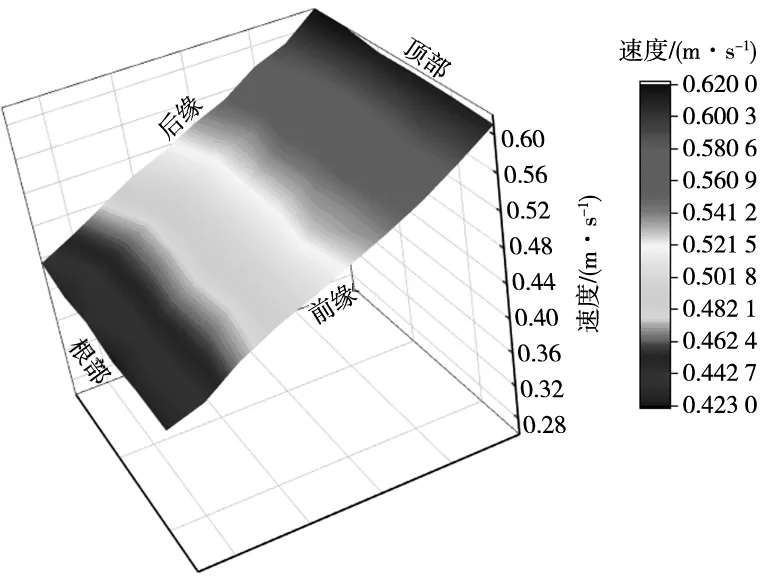
(a)振动回转式加工正面滚抛磨块速度

与图8对比可见，回转式加工P1处与P10处滚抛磨块速度差值为0.256 m/s～0.318 m/s，振动回转式则是0.183 m/s～0.186 m/s；振动式加工F1、F6处与中间区域滚抛磨块速度差值为0.028 m/s～0.054 m/s，振动回转式则是0.002 4 m/s～0.009 2 m/s。

如图13所示为不同加工方式下滚抛磨块速度的变异系数。

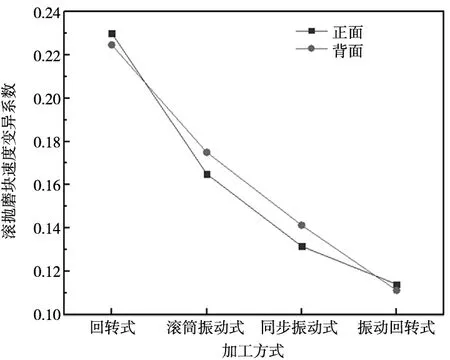
图13 滚抛磨块速度变异系数

由图可见，回转式、滚筒振动式、同步振动式和振动回转式加工的滚抛磨块速度的变异系数依次递减，正面和背面分别为0.229 97和0.224 57、0.163 25和0.171 36、0.131 59和0.141 33、0.114 03和0.111 27。相较于回转式和振动式，振动回转式的方案会缩短模拟件表面不同区域滚抛磨块的速度差值。

如图14所示为振动回转式加工后的模拟件表面不同区域的磨损量。

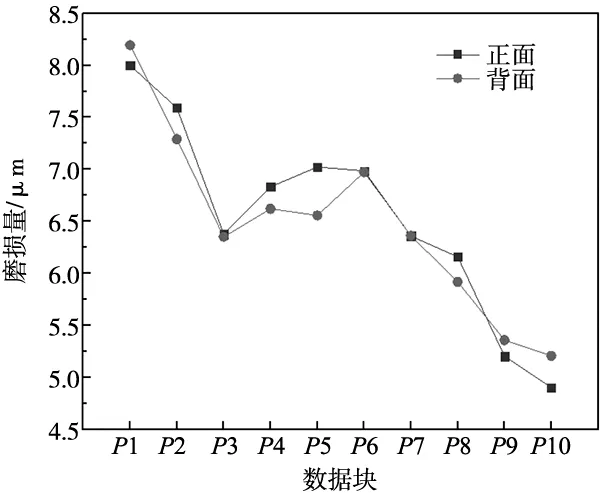
(a)叶尖到叶根磨损

由图可见，磨损量从P1处～P10处整体为递减趋势，P1处的磨损量约为P10处的1.57～1.61倍，相较于回转式及振动式，振动回转式缩短了P1～P10处的磨损量差值。磨损量从F1处～F6处为先减后增趋势，F1、F6处的磨损量约为中间区域的1.81～1.90倍，相较于回转式及振动式缩短了F1～F6处的磨损量差值。与图7对比可见，振动回转式与回转式、振动式的磨损规律相似，但缩短了不同区域的磨损量差值。

根据仿真结果可知，从加工效率及加工均匀一致性的角度考虑，振动回转式优于回转式及振动式。通过离散元法的模拟可以对整体叶盘振动回转式的加工提供参考，为下一步的实验研究打下理论基础。需要注意的是仿真过程中磨损量会随着时间的增加而增长，而实际加工中材料去除量会经过一定时间后趋于稳定，继续加工一段时间可能还会继续增大。

3 结论

本文基于航空发动机整体叶盘加工不均匀的问题，仿真并对比分析了几种抛磨加工的优缺点，根据其优缺点提出了振动回转式抛磨加工并进行了仿真分析。仿真结果表明，相较于回转式和振动式加工，振动回转式抛磨加工缩短了模拟件不同区域磨损量差值和滚抛磨块速度差值，提高了加工效率及加工均匀一致性。振动回转式加工解决了纯回转、纯振动这种单一运动的加工方式在加工整体叶盘中存在的不足，为抛磨加工在整体叶盘表面加工方向的应用奠定理论基础。