基于Copula函数模型的圆柱滚子轴承旋转精度分析

魏建波，朱建新，满维伟

(中国航发湖南动力机械研究所，湖南 株洲 412002)

0 引言

滚动轴承是旋转机械设备中极为重要的支承构件，其旋转精度是影响整个设备运转精度和可靠性的重要因素。轴承在加工过程中不可避免地产生各种尺寸误差，进而影响轴承的旋转精度，其中滚子存在直径误差时会显著降低轴承旋转精度，因此开展轴承滚子直径误差与轴承旋转精度的相关性研究，对提高轴承生产质量具有重要意义。

Copula函数理论广泛应用于水文、金融等各项领域中。近年来众多学者在各项领域进行深入研究：沈小军等[1]基于Copula函数理论建立风电机组间风速相关性计算方法，并针对某一地区的运行数据进行了案例分析。吴建华等[2]分析了Copula函数选择的难点，提出了基于参数Bootstrap技术的对数似然准则检验方法，并利用模拟实验检验了该方法的有效性。张蕾等[3]研究了基于Copula函数的抗剪强度参数联合分布模型对岩土结构物系统可靠性的影响规律，揭示了抗剪强度参数间相关结构对岩土结构物系统可靠度影响的过程。尤琦英等[4]分析了不同Copula函数参数估计法对函数类型选择及对河流年径流遭遇丰枯期的影响。指出极大似然估计法的拟合结果略优于Kendall系数估计法，但两种参数估计方法针对Copula函数类型选择都是可行的。李玉敦等[5]基于Copula函数和马尔科夫过程理论，提出了一种多维时序风速相依模型及该模型的两阶段蒙特卡洛模拟方法。张尧庭[6]讨论了Copula函数在金融市场分析方面的应用前景。史道济等[7]分析了沪深股票市场间的相关性。国外学者提出了两阶段极大似然估计法来进行二元Copula函数的参数估计[8-9]。ENGLE等[10]提出了一种用样本经验分布代替边际分布函数值的半参数估计法。可见Copula函数在分析变量间的非线性相关性方面，具有一定的基础和优势，但是目前将Copula函数用于研究轴承旋转精度的文章还少见报道。

本文以圆柱滚子轴承为例，利用Copula函数这一有力手段来研究滚子尺寸误差与轴承径向跳动之间的关系，并建立了数学分析模型，并对模型的合理性进行了验证。利用建立的数学模型计算了两者间的相依性条件概率，为深入研究轴承元件尺寸误差与轴承旋转精度的关系，提供了新的研究思路。

1 特征变量的获取与分析

将轴承中其中两个相邻滚子的直径尺寸误差和轴承径向跳动数据作为研究变量。根据对滚子尺寸检测数据的统计分析，用正态随机数生成两组滚子尺寸误差数据，并分别记为w1、w2。以w1、w2为输入条件，获得相应的轴承径向跳动数据s。由仿真程序得到的各特征变量参数如表1所示。

表1 特征变量的边缘分布参数

利用Kolmogorov-Smirnov检验法[11](以下简称K-S检验法)对各特征变量的边缘分布函数进行正态分布检验。结果如表2所示。

表2 Kolmogorov-Smirnov单样本检验中的D值

由上表可知的各特征变量的D值均不大于0.215，伴随概率P均不小于0.05，所以可以认为三组特征变量均符合正态分布。

2 模型的优选、建立及验证

Copula函数的模型具有多种多样的类型，本文将从常用的5种Copula函数中优选出最适宜的模型。优选依据为不同类型Copula函数的均方根误差[12]，优选结果分别如表3和表4所示。

表3 5种模型的均方根误差(1号滚子)

表4 5种模型的均方根误差(2号滚子)

由上表可知，Gumbel-Copula函数误差最小，为本文最优的建模选择。

根据Copula函数相关理论，只要已知特征变量的连接函数及各自的边缘分布函数即可建立出相应的函数模型：

(1)

式中，u(w)、v(s)为边缘分布；θ为建模参数。

通过对比计算模型的经验累积概率值和理论累积概率值的相关性来验证模型的合理性。

由仿真程序计算得出两特征变量的相关系数分别为0.982和0.981，显示了两者间的显著相关性，表明了模型的合理性。

3 相关性分析

本文分别计算了基于样本数据的Kendall系数τ、基于Copula函数的Kendall系数和Spearman秩相关系数ρn来对比分析表征变量间的相关性。

由表1可知，生成的两组滚子直径误差数据中，两者的均值相当，但第二组数据的方差更小，结合表5分析可得到以下结论：

表5 1,2号滚子存在误差时特征变量间的秩相关系数τ

(1)滚子直径尺寸误差值与轴承径向跳动量之间存在显著的相关性。当两个相邻滚子的尺寸误差具有不同的均值与方差时，两个滚子尺寸误差与轴承径向跳动的秩相关系数分别为0.511 7、0.637 3。

(2)滚子直径尺寸误差数据组方差的大小不仅代表着滚子误差数据的集中与分散，也表征了该组数据与轴承径向跳动相关系数的大小。

由上述结果可得：滚子尺寸误差与轴承径向跳动相关性较强；Copula函数能较好的分析特征变量间的相关性。

4 基于Copula函数的条件概率计算

当轴承零部件存在一定尺寸误差时，轴承径向跳动的变化是未知的，但通过Copula函数可以对轴承径向跳动超出值的概率进行预测；同理在轴承旋转精度即跳动一定时，也可以准确预测轴承滚子误差的超出概率。下面对基于Sklar定理建立的Copula函数条件概率计算方法进行介绍：

在二维Copula函数中，设F(x1,x2)=P(X1≤x1,X2≤x2)=C(u,v)，对于条件概率，可以通过Copula函数获得在X1=x1条件下，事件X2≤x2的条件概率为：

F(X2≤x2|X1=x1)=P(X2≤x2|X1=x1)=

(2)

用式(1)所示Gumbel-Copula函数，进行基于Copula函数的条件概率预测。设定轴承滚子尺寸误差为0.01 mm～0.1 mm，间距为0.01 mm，分别计算轴承径向跳动大于0.03 mm、0.05 mm、0.07 mm的超出概率；同理设定轴承径向跳动为0.01 mm～0.1 mm，间距为0.01 mm，分别计算W1组滚子尺寸误差大于0.03 mm、0.05 mm、0.07 mm的超出概率，计算结果如图1、图2所示。

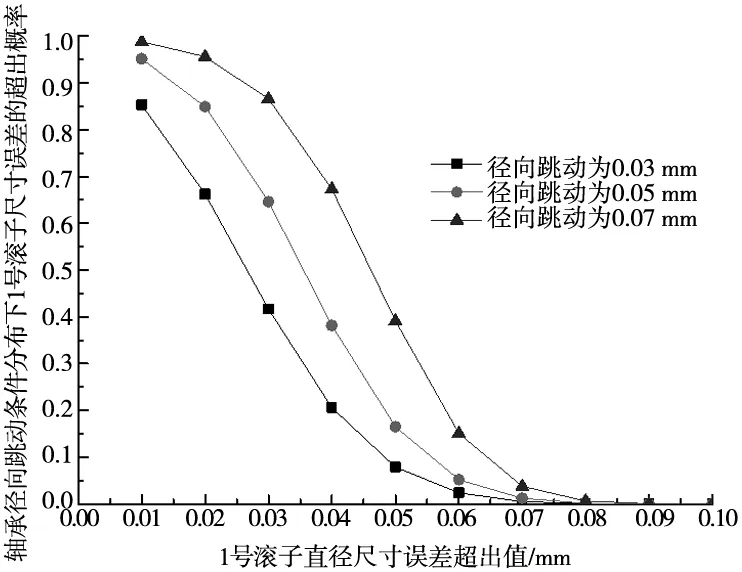
图1 轴承径向跳动不变时基于Gumbel-Copula函数的1号滚子尺寸误差超出概率

图2 1号滚子误差不变时基于Gumbel-Copula函数的轴承径向跳动超出概率

可以得出：

(1)当轴承滚子的尺寸误差逐渐增大时，基于Gumbel-Copula函数条件概率下的轴承滚子尺寸误差超出概率不断减小。

(2)同一滚子尺寸误差下，轴承径向跳动越小，滚子尺寸误差的超出概率越小；轴承径向跳动越大，滚子尺寸误差的超出概率越大。变化趋势线均呈非线性。

(3)当轴承滚子尺寸误差不变时，轴承径向跳动的超出概率随轴承径向跳动超出值的增大不断减小。

同理，针对W2组滚子做相同处理，计算结果如图3、图4所示。

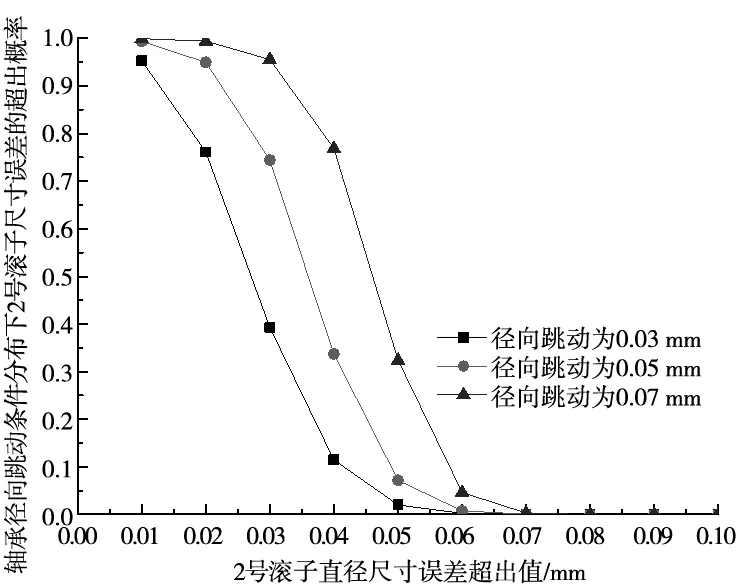
图3 轴承径向跳动不变时基于Gumbel-Copula函数的2号滚子尺寸误差超出概率

图4 2号滚子误差不变时基于Gumbel-Copula函数的轴承径向跳动超出概率

对比图1与图3，图2与图4，得出：

(1)在不同的Gumbel-Copula函数建模参数、滚子尺寸误差分布特征下，基于Gumbel-Copula函数的条件概率曲线呈现出相同的变化趋势；

(2)方差越小，滚子尺寸误差超出概率的减小趋势更为陡峭；但随着尺寸误差的增大到0.07 mm后，滚子的尺寸误差超出概率均逐步趋近于0，即滚子尺寸误差分布的特征参数对条件概率值有一定影响。

5 结论

(1)Copula函数可以作为研究轴承旋转精度的有效手段，但不同类型的Copula函数对相同数据间相依性的评估结果有明显差别，需要进行拟合优度评价，选出最优的Copula函数模型。

(2)滚子直径尺寸误差与轴承径向跳动的相关性较强。滚子尺寸误差数据分布的特征参数会影响滚子直径尺寸误差与轴承径向跳动的秩相关系数。

(3)通过Gumbel-Copula函数能较为地准确分析轴承径向跳动与滚子尺寸误差之间的相关性。

通过Gumbel-Copula函数进行条件概率分析，可以合理选择一定直径尺寸范围内的滚子进行装配，有利于保证轴承的旋转精度。