螺栓结合面的三维弹塑性接触的有限元分析*

何勇辉，朱子文，张二亮，何声馨

(郑州大学机械与动力工程学院，郑州 450001)

0 引言

对于机床和大部分的机械结构，它们都是由若干个零件装配而成，相互接触的零件表面之间形成结合面[1]。螺栓连接结构是最为常用的一种机械连接方式，受表面粗糙度的影响，通过螺栓连接起来的两个零件的结合面在受到外部加载下会发生弹塑性变形，因此结合面表现出复杂的力学特性。为了能够更加深入的探究结合面在接触过程的变形和接触机理，从微观角度上研究结合面的表面粗糙度与接触模型、弹塑性变形以及能量损耗规律，一直都是研究的热点和难点问题。

在国外，GREENWOOD等[2]假设粗糙表面轮廓峰高服从正态分布，利用概率统计分析的方法创建了粗糙表面弹性接触模型(GW模型)，该模型只考虑了接触初期的弹性变形。CHANG等[3]通过把粗糙表面微凸体的变形划分为纯弹性变形和纯塑性变形两个历程，改善了GW模型，但缺少对弹塑性变形过渡过程的刻画。KOGUT等[4]通过对单微凸体进行有限元分析，探究了在接触过程中微凸体发生纯弹性、弹塑性和纯塑性变形区域的界定范围，并用指数函数建立了接触的力、负载和面积与微凸体的变形量之间的关系式。COHEN等[5]结合赫兹理论和BRIZMER等[6-7]的分析结果，建立了粗糙表面的全粘接接触模型。在国内，尤晋闽等[8]基于GW模型，充分考虑了微凸体的弹性、弹塑性及完全塑性等不同变形机制，提出了结合面的统计模型。高飞翔[9]利用修正过的分形函数，构建了圆柱与平板的有限元接触模型，分析了算术平均高度对接触面积的影响。赵波、甘立等[10-11]建立和分析了二维的弹塑性接触模型。

表面粗糙度对于机械组件的工作状态、耐磨性、服役寿命和疲劳强度具有重要影响[12]。Rq值越小的表面可以承受高载荷而不造成表面损伤[13]。表面算术平均高度Sa在工程中常用来描述精密加工表面粗糙度，它能够反应全局的高度特征。王栋等[14]研究了三维表面粗糙度参数Sa对疲劳寿命的影响,降低Sa可以提高试样的疲劳寿命。

文献中大多是从单个微凸体展开理论研究，对三维模型研究颇少。为了更加深入地研究结合面的变形和接触机理，使得构建的接触模型更接近工程实际工况。本文基于实测的三维形貌数据，建立了螺栓结合面的三维弹塑性接触模型，提出了一种预测表面三维形貌的方法，研究了不同加载力下三维表面粗糙度参数的变化。通过比较试验和仿真数据，验证了数值模型的有效性。

1 试验研究

1.1 螺栓加载试验

试验所用的平板，一个是经过抛光处理，而另一个是粗糙的平板。抛光平板为18CrNiMo7-6，以下称为抛光板。首先用60#～5000#的砂纸对抛光板进行研磨，然后用粒度为2.5 μm和1.5 μm 金刚石磨粒对其进行抛光研磨。粗糙的平板为经过固溶处理后的316奥氏体不锈钢，以下称为粗糙板。其表面使用60#砂纸进行研磨。研磨均在抛光机上进行。抛光板和粗糙板的表面粗糙度、硬度及几何参数如表1所示。

表1 抛光板和粗糙板的表面粗糙度、硬度及几何参数

本文通过螺栓预紧来生成两个板之间的夹紧力，如图1所示。螺栓预紧力F与拧紧力矩T的关系取决于螺距、螺栓直径以及螺母与螺栓之间的摩擦系数[15-16]。

图1 螺栓加载试验及受力示意图

T=Kd×F

(1)

式中，K为螺母与螺栓之间的摩擦系数；d为螺栓公称直径。

采用M6标准螺栓，螺栓两侧平垫片尺寸为φ10 mm×φ6.4 mm。通过数显扭矩扳手对螺栓施加扭矩，为防止试样在拧紧过程中发生旋转滑动，抛光板与粗糙板放置在宽度为20.5 mm的凹槽里，通过改变扭矩来产生所需的载荷。共做了两组试验，选取的扭矩分别为5 N·m和15 N·m，根据公式(1)计算得到预紧力分别为4 166.7 N和12 500 N。预紧力通过垫片施加在试件上，在垫片压紧的位置其分别对应89.99 MPa和269.98 MPa的应力。

1.2 材料参数的测定

本文通过拉伸试验来获得研究真实的弹塑性变形所需的粗糙板材料的本构关系参数。拉伸实验所用的试样在车床上加工而成，试样尺寸按照《ISO6892-1:2009,MOD》标准规定设计。试验所用设备为MTS万能试验机，采用应变控制，应变速率为5×10-4s-1。测得的应力应变数据如表2所示。由拉伸试验所得的应力应变曲线计算弹性阶段的斜率，即粗糙板弹性模量为121.7 GPa。

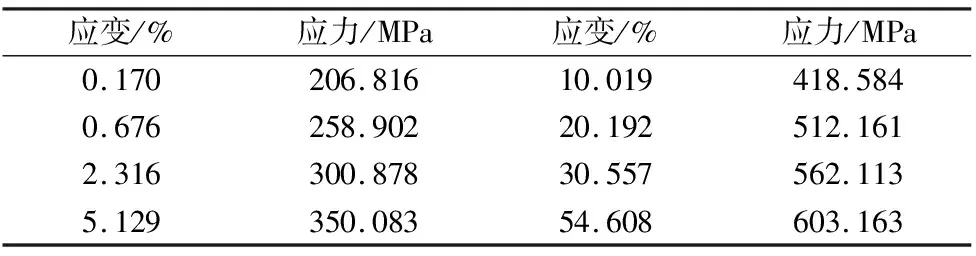
表2 应力应变数据

2 参数化有限元模型及表面粗糙度预测

2.1 三维形貌的测量

以抛光板和粗糙板试样垫片压紧位置为测量区域。通过NPFLEX型三维形貌测量仪获得抛光金属和粗糙表面的三维表面形貌数据。该设备是利用白光干涉机理，白光照射在试样表面，通过显微镜得到试样表面的干涉条纹，从而获得试样的表面形貌数据。形貌测量采用物镜为20倍的长焦镜头，目镜为0.75倍镜头。由于测量过程中受到白噪声的影响，本文利用中值滤波的方法对采集的三维形貌数据进行平滑降噪，得到的三维形貌如图2a所示。本文选用取样面积为0.99 mm×0.50 mm的数据进行建模，表面形貌数据由199×101个数据点组成。

2.2 弹塑性接触模型

抛光板算术平均高度Sa为25 nm，且相对硬度较高，为了简化模型，把抛光板简化为一个光滑的刚性表面。根据取样面积和节省计算量的考虑，在保证精度的前提下，取粗糙板的模型尺寸为0.99 mm×0.50 mm×0.20 mm。

本文使用ANSYS系统参数化设计语言(APDL)进行建模研究。三维参数化模型的生成步骤如下：

(1)使用循环命令读取实测三维形貌数据点坐标生成关键点；

(2)使用循环命令使X方向的关键点依次连接成线，同理，将Y方向的关键点也依次连接成线；

(3)通过位置选择单个小区域的线，由于关键点不共面，利用孔斯曲面拟合生成面，然后通过循环命令将所有小区域重构为连续的几何粗糙表面；

(4)在生成的粗糙面4个角下方创建4个关键点，通过自下而上的实体建模方法创建实体模型。

取粗糙面最高点处创建刚性面，刚性面尺寸与粗糙板长宽相同。粗糙板实体采用智能网格划分方法，网格密度从粗糙表面到远端逐渐减小，以减少单元总数。模型采用实体solid187单元，使用接触单元conta174单元和目标单元targe170完成了接触对设置。刚性面网格划分为targe170单元，粗糙表面网格划分为conta174单元。应用增广拉格朗日接触算法。采用多线性等向强化(MISO)塑性选项，输入的应力应变数据(见表2)和弹性模量为拉伸试验所得，泊松比取0.3。最后进行边界条件设置，约束粗糙板实体底面Z方向位移，同样对垂直实体侧表面方向的位移进行了约束。在刚性面的一个角处创建一个先导节点，约束先导节点进而将边界条件应用于该表面，从而消除了向单个节点分配边界条件的需要，并减少了出错的机会。对先导节点施加X、Y方向约束，保留Z方向移动。建立的接触模型如图2b所示。

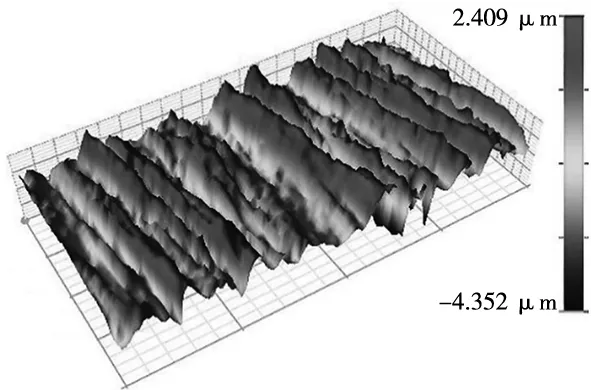
(a)实测三维形貌

2.3 预测表面粗糙度的方法

螺栓结合面受压后由于发生塑性变形，其表面粗糙度发生变化。本文基于有限元分析结果，提出了一种变形后表面粗糙度变化的预测方法。有限元分析载荷由两步组成，第一步施加压力，第二步卸载到初始状态。通过提取粗糙板表面节点的坐标值和变形量，将坐标值和变形量进行叠加，叠加的值减去模型高度值即可获得变形后的粗糙板表面的三维形貌数据。

选用三维表面粗糙度参数来表征表面粗糙度的变化。通过根据参数的定义编写的MATLAB程序计算算术平均高度Sa、表面倾斜度Ssk、均方根高度Sq和表面最大高度Sz、表面最大峰高Sp、表面峭度Sku、最大谷深Sv[17]。

3 结果分析与讨论

利用建立的弹塑性有限元模型，通过先导节点向刚性面分别施加了89.98 MPa和269.98 MPa的压力，对三维弹塑性接触模型进行准静态分析计算。

3.1 粗糙板的应力与应变分布

两组不同压力下粗糙板的应力和应变分布，如图3所示。最大Von Mises应力均出现在粗糙面的波峰处，应力分布呈现一定规律，即沿最大应力处向外延伸，应力逐渐降低。随着加载的增加，最大Von Mises应力的最大值也在增加，应力分布范围也在增加。如图3a的应力云图所示，在同一个水平截面上应力值大小不一，其中一部分区域的应力值在屈服强度以下，其余值超过了屈服强度，这符合螺栓结合面实际接触变形机制，也表明考虑微凸体对分析结合面的接触变形机理的重要性。对比接触压力结果可得，随着载荷的增加,接触压力逐渐增加，接触面积也在增加。由于粗糙表面凹凸不平,局部Von Mises应力很大，当最大Von Mises应力超过了材料的屈服强度,粗糙面就会产生塑性变形，从而增加了接触面积,直到光滑平面与粗糙板的接触处于平衡状态，接触只发生在粗糙表面的峰之间。两种压力下塑性变形结果表明，两种载荷下粗糙表面均发生了塑形变形，随着加载增加，最大塑形变形量增加，粗糙面发生塑性变形的面积亦增加。

(a)Von mises应力 (b)接触压力

3.2 三维表面粗糙度预测

选取评价长度L=0.99 mm的数据，试验所得的表面粗糙度轮廓的测量结果如图4所示。由图4可知，随着装配载荷的增加，表面粗糙度峰值高度逐渐降低。传统的粗糙度基于二维粗糙度轮廓进行评定，不能够完整地反映整个表面的全部信息。

表面形貌的三维评定从整体上对零件表面特征进行描述，具有全局性。将提取的三维形貌数据导入MATLAB计算软件，重构受压后的三维表面，从而得到预测的三维形貌，图5是载荷为289.98 MPa时重构的三维表面。三维表面粗糙度参数能从多个角度表征螺栓结合面的接触变形过程。试验和仿真得到的三维表面粗糙度参数值如表3所示。随着载荷的增加，试验和仿真的三维粗糙度参数Sa、Sq、Sp、Sv和Sz都逐渐降低，这是由于塑性变形导致整个表面高度发生了变化。试验和仿真的Ssk值均小于0，表明粗糙度峰值高度分布相对于平均面偏上，这也验证了微凸体峰是持久存在的；试验载荷为289.98 MPa的Sku值约等于3，说明高度分布尖缓并存，而其它试验和仿真的Sku值均大于3，说明高度分布较为尖锐。参数Ssk和Sku反映了表面形貌的高度分布变化。试验和形貌测量引入了随机误差(如无法保证测量区域一致性)，但仿真结果和实验结果整体吻合较好，仿真结果可靠。

图5 基于有限元分析结果预测的三维形貌

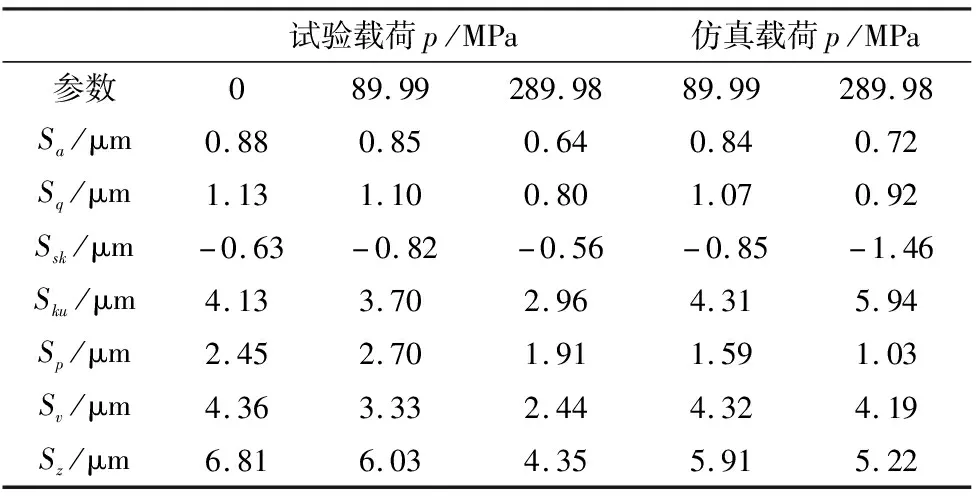
表3 不同压力下的三维粗糙度参数值

4 结论

本文利用实测的三维形貌数据，建立了螺栓结合面三维有限元接触模型的参数化生成方法，开展了数值分析与模型验证。主要结论如下：

(1)本文全面刻画了螺栓结合面接触的弹塑性变形过程，最大的Von Mises应力发生在粗糙表面轮廓的波峰处，应力分布沿最大应力处向外延伸，应力逐渐降低，符合实际情况。

(2)本文基于有限元分析结果，重构了受压后的三维形貌，为表面粗糙度的预测提供了有效途径。

(3)试验与数值模拟的结果表明，三维粗糙度参数Sa、Sq、Sp、Sv和Sz反映了结合面接触变形的高度值变化，随着载荷的增加，其参数值逐渐降低，参数Ssk和Sku反映了表面形貌的高度分布变化；建立的参数化三维有限元接触模型较为完整地还原了螺栓结合面真实的三维形貌，具有较高的建模精度。