基于叠加授权和TOPSIS的绿色车间方案优化

李汶俊，汪永超，张栩静，毛凯宁，周 涛

(四川大学机械工程学院，成都 610065)

0 引言

我国的发展进入了新阶段，同时制造产业转型升级进入关键时期，国家提出绿色的发展理念，走生态文明的发展道路已然成为定局。通过大力号召与政策文件来落实绿色制造的方式方法，可以实现从底层生产到上层流通的全环节覆盖[1]。应该看到，底层的制造加工环节在产品的生命周期中有着至关重要的作用。如何对制造加工车间的升级优化方案进行合理选择，以减少底层资源消耗，实现绿色生产，是我们亟待解决的问题。

关于方案的优选评价，目前已累积了多种方式。李远远等[2]提出通过ANP进行主观授权，同时联合EWM进行客观授权，最后用理想点法对绿色施工方案进行综合评价，从而选择最优施工方案。岳丹丹等[3]运用层次分析法，建立灰色关联决策模型，对矿排水系统设计的多种优化方案进行综合评价。郭培震[4]建立了投影寻踪分类模型和熵权系数评价模型，并使用主成分分析法来减少主观权重的影响，从而选出南水北调配套工程最优方案。

目前有关制造加工车间优化方案评价模型和方法比较缺乏，总结关于各类方案的评价方式，主要都是通过主观成分或经验对方案进行评价，评价要素单一，具有模糊性和主观性，缺少定量分析，因此本文提出通过TFN-AHP[5](三角模糊层次分析理论)和CRITIC法[6]相结合的叠加授权算法对每一层次各指标的重要度进行分析，兼具定性和定量的优势，求得每个指标所占权重，然后使用TOPSIS法[7]对各个方案进行关联评价，最终选出最合理的绿色制造车间优化方案。这种方法相较于传统的经验评价或单一要素评价更具普遍性和科学性。

1 建立分层模型

对机械加工车间的优化改进有多个方面，传统的优化方案更多关注生产成本和生产能力，但绿色化的改进方案兼顾可持续发展，需要添加环境友好要素和资源节约要素，在此基础上建立车间的优化评价体系，将车间的优化要素分为车间生产效能、环境友好度、生产质量、车间改进成本、车间改进时间五个指标，包括其下属的扩建规模等共13个分指标，建立如表1所示的绿色制造车间优化模型。

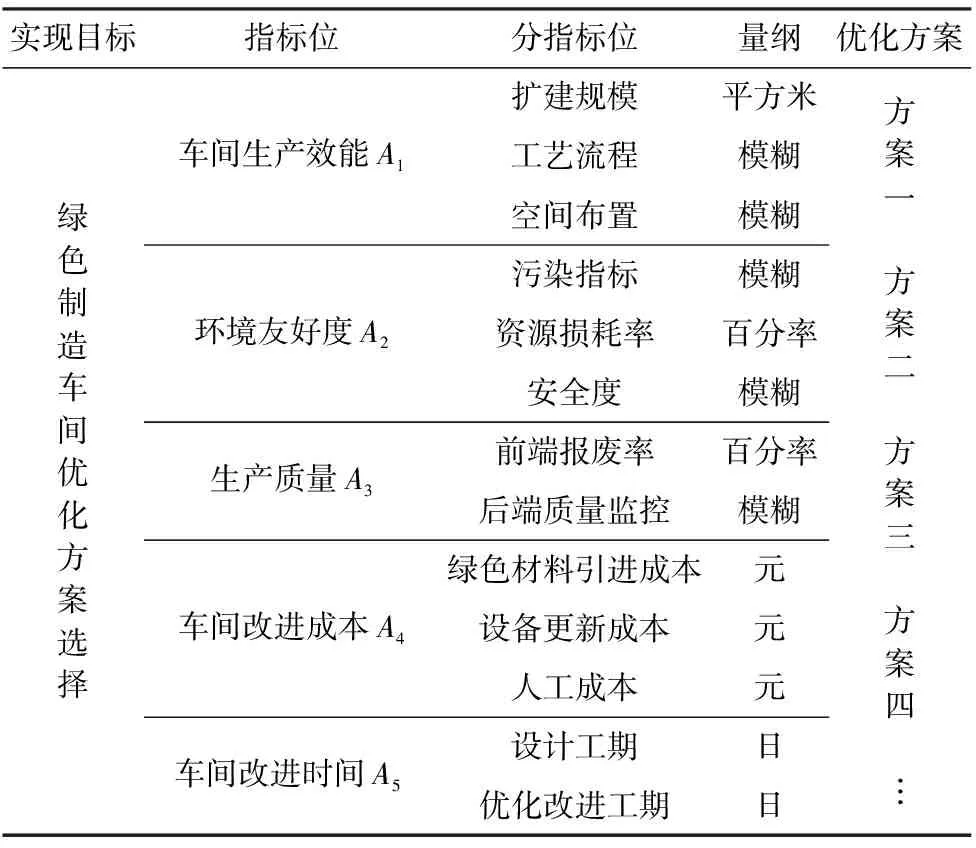
表1 绿色制造车间优化模型

2 模型求解分析

建立绿色制造车间优化方案评价模型后，需要依层次分别确定指标位和分指标位每个因素所占权重及在层次总的权重。文章使用三角模糊数学理论，参考一定数量的专家团对各指标重要度的主观经验评价，同时使用CRITIC方法，加入了客观评价的权重，通过对两种权重叠加授权求得各指标所占比例，最后用TOPSIS方法将现有的方案各指标关联对比，对模型进行评估，求得最优解。

2.1 三角模糊数学层次分析

本方法以层次分析法[8](AHP)为基础，考虑到不同要素之间的相对重要度模糊且存在一定浮动，故引入了三角模糊数，对要素相互比较的重要程度进行规定范围的量化判定，该方法比传统的层次分析方式更合理。

2.1.1 定义三角模糊数

三角模糊数的提出是为了解决不确定环境下的问题[9]，在各指标的比较矩阵里面，我们用模糊数aij=(a,b,c)来表示指标xi比xj的重要程度，其中，b表示可能性最大的值，a和c表示该可能性的上限和下限，a和c的距离越远，模糊程度会相应提高。

另外，三角模糊数的运算规则与四则运算的规则一致，设Q1=(a1,b1,c1)，Q2=(a2,b2,c2)两个模糊数运算时，将内部的a，b，c分别进行算数运算操作。同时规定Q1>Q2的可能度函数t(Q1>Q2)为：

(1)

2.1.2 建立模糊矩阵

操作时，先让某一层各个指标进行两两比较，判断出每个位置的三角模糊数aij=(a,b,c)，这是由专家团打分得到，A1-An为该层的n个指标，CS表示该层的上属指标，aij表示Ai相对于Aj的重要程度，该程度使用1～9的单整数进行标度，标度规则如表2所示，由此构建CS层下属指标的三角模糊矩阵如表3所示。

表2 单整数标度规则

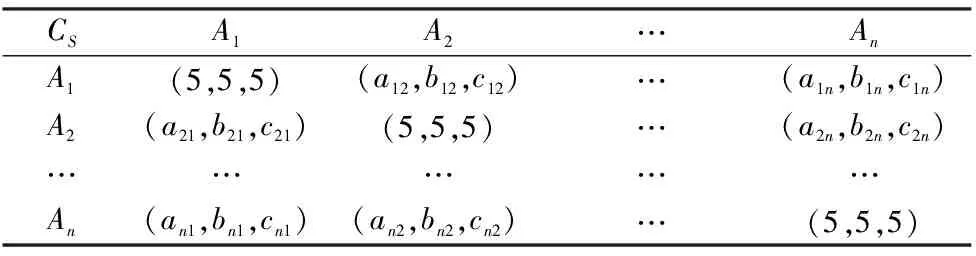
表3 Cs下属层的三角模糊矩阵

2.1.3 求得指标权重

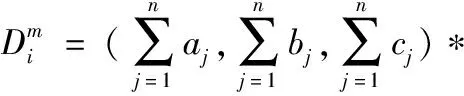
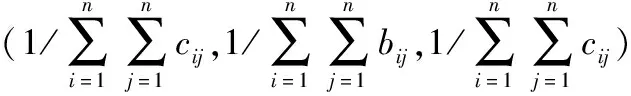
(2)

(2)计算第m层终权重及在层次所占总权重

初始权重还具有三角模糊数的浮动性特征，需要对其进一步处理。在多组三角模糊数的重要度比较中，利用可能度函数的概念，量化处理三角模糊数，使其能够进行大小比较，具体计算公式如下：

dp=mint(Dp≥Di),p,i=1,2,...,n且p≠i

(3)

规范化m层的权重后，得到终权重：

(4)

wm=(w1,w2,...,wn)

(5)

再此基础上计算层次的总权重：

(6)

其中，上角标表示为层次数，下角标表示该层次对应的上层次的单指标。

最后的层次所有指标分得的权重为：

W*=(W1,W2,...,Wn)

(7)

其中，n为末层指标个数。

2.2 CRITIC法分析

客观赋权的方法有很多种，包括EWM法[10]、均方差法[11]等在内，但是赋权的结果都存在不够全面、客观的问题，而本文采用CRITIC法。在CRITIC法中，综合反映相同指标离散程度的标准差大小和不同指标之间的关联性强弱这两个要素[12]，所得结果更科学和全面。

2.2.1 标准评价矩阵构造

根据各方案制定的标准，列出数据原始矩阵Ac×d，则矩阵内xij表示第j个方案的第i个指标。

有的评价指标如安全度、污染指标等只能模糊比较，没有量化标准，所以要转化为模糊性数字语言，转化规则在下文根据实例确定；又各指标之间量纲不同，数据大小级别不同，不存在可比性，所以需要进行标准化处理，使其全部映射在[0,1]之间，我们采用如下的规则进行规范化处理：

对于正向指标，数据越大越好：

(8)

对于逆向指标，数据越小越好：

(9)

由此可以得到标准评价矩阵:

(10)

2.2.2 数据综合评判

客观评价各指标所占权重，需要综合两方面的因素：

第一，考虑不同方案同一评价指标之间的差异性和相关程度，用标准差进行评判。标准差越大，表明指标值的变异程度越大，包含的信息量越大，指标影响力越大，其权重就越大，反之亦然。标准差的计算如下：

(11)

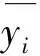
第二，考虑各个方案某一评价指标与其他评价指标之间的相关性，用相关系数的逆向量化指标1-|r|进行评判。通常，相关系数越小，其逆指标越大，变异程度就越大，包含的信息量越大，指标影响力越大，所占权重越大，反之亦然。相关系数的计算如下：

(12)

相关系数rcd表示第c个指标与第d个指标的相关程度。需要注意的是，当c=d时，相关系数为1；且rcd=rdc。

由此可得出如下的评判依据：

(13)

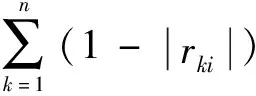
2.2.3 权重计算

对评判依据ηi进行标准化处理，可得到客观评判的终权重：

(14)

2.3 叠加授权

在求得主客观权重的基础上，本文将两种权重影响因子进行叠加，使得各指标的权重更具有适普性和客观性。其计算公式如下：

(15)

其中，i=1,2,...,n，n为指标数。

V*=(V1,V2,...,Vn)

(16)

3 基于TOPSIS法的方案关联评价

TOPSIS法对于多指标关联求解有着极大的优势[13]，通过对各方案同一指标分别建立最优理想点的方式，比较各指标与理想点距离的大小，综合各指标所占权重因素对方案理想程度进行排序，从而得到最优解，具体算法见下文。

3.1 判断矩阵加权标准化

首先构造判断矩阵，矩阵构造方式与CRITIC法一致。同时，需要对判断矩阵进行标准化处理，规范矩阵数值区间处于(0,1)且与之前保持趋同。处理方法如下：

(17)

得到规范矩阵Yi×j。

标准化处理只考虑能规范和关联各要素，但不能体现各要素的重要程度，所以需要加入权重因素对矩阵内的数据予以修正，完善决策体系。本文加入的是叠加授权后的权重。得到加权标准化矩阵：

(18)

3.2 理想点集距离判断

指标强弱判断存在两种情况，一是效应性指标，如安全度，通常指标越大，越接近理想状态；二是成本性指标，如人工成本，通常指标越小，越接近理想状态。

规定正理想点为最接近理想状态，负理想点为最偏离理想状态。求各要素正理想点集P+，设效应性要素为E+，成本性要素为E-，有：

(19)

同理，可求负理想点集：

(20)

其中，i为各组成要素，即评价指标。

在正理想点集之内，规定总距离为：

(21)

在负理想点集之内，同理可得：

(22)

3.3 相对偏离度计算

综合考虑各指标到最理想点的距离和最偏离点的距离，计算相对偏离度G，G表示与理想点集偏差的程度，G越小，偏差程度越小；反之，则大。G的计算公式如下：

(23)

其中，j表示方案数。Gj最小，即为最优方案。

4 实例分析

以一家科技企业为例，来验证算法的合理性以及实用性。该企业为了响应国家号召以及自身发展的需要，对其附属的基础配件底层加工车间进行产业升级改造，综合考虑优化改造的效果、时间、成本以及环境友好性等要素，有F1、F2、F3、F4这4种方案可供选择，各方案的要素对比如表4所示。利用上述算法对4种方案进行关联分析，得出最佳方案。

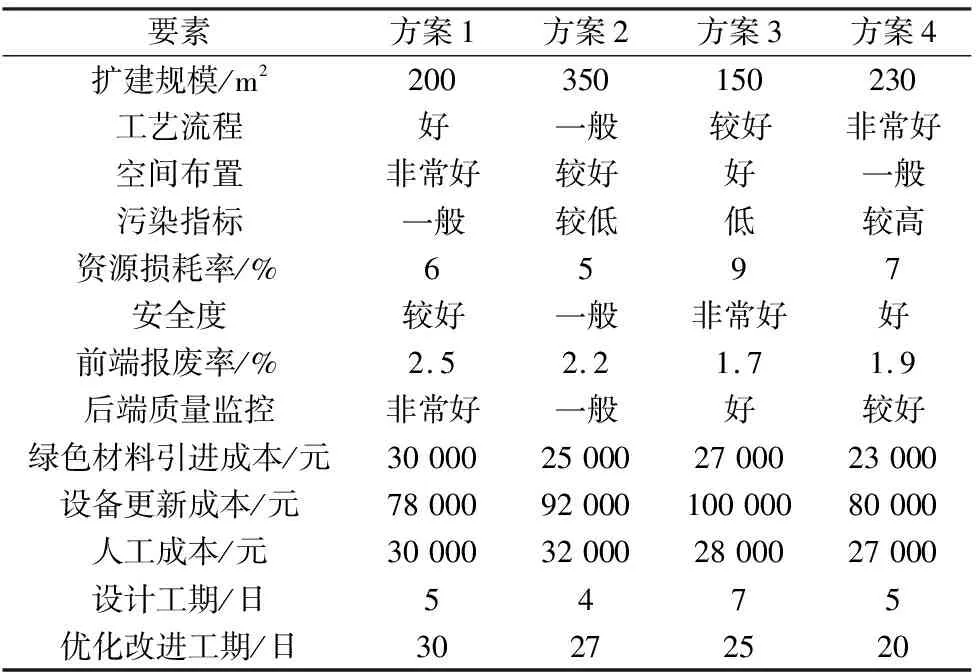
表4 4种方案要素对比

4.1 各指标叠加授权权重确定

(1)计算主观权重

先由两个专家团对指标位的共5个指标进行两两对比评价，采用三角模糊数对其打分，使用单整数的标度方法，统一专家意见后，得到了如下的三角模糊数评价表：

表5 专家意见下的三角模糊评价表

取平均值后，得到如下的三角模糊数评价矩阵：

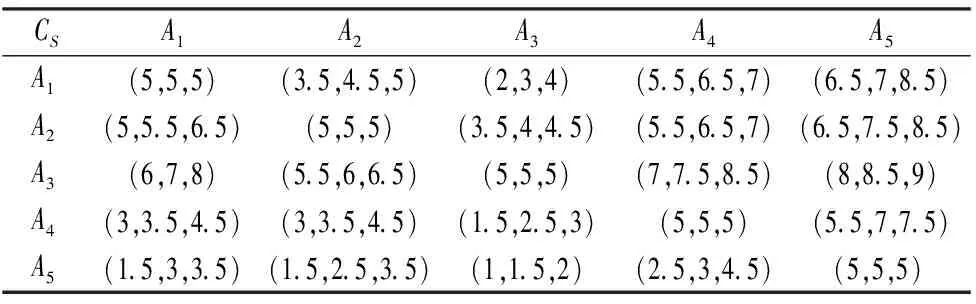
表6 三角模糊评价矩阵

由式(2)、式(3)，对指标位各指标求初始权重并去模糊化处理，可得：

d1=0.429，d2=0.600，d3=1.000，d4=0.366，d5=0.298

标准化处理后，由式(4)可得到指标位各指标的终权重：

w=(0.159,0.223,0.371,0.136,0.111)

同理，分指标位的各个指标所占权重大小也可由初始层的计算方式得到，每一个指标在对应层次下的权重比例如表7～表11所示。其中，总权重由式(5)、式(6)求得。

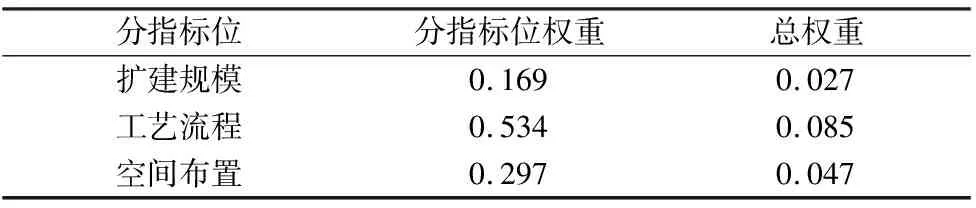
表7 车间生产效能层下的权重及总权重

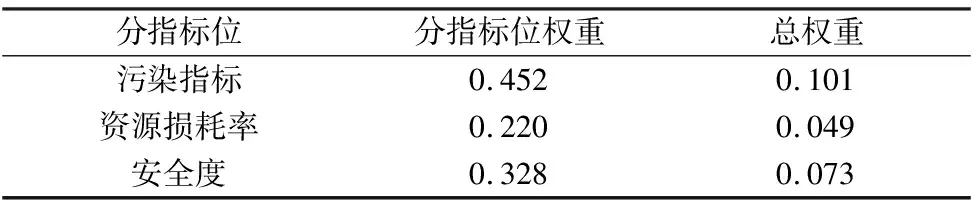
表8 环境友好度层下的权重及总权重

表9 生产质量层下的权重及总权重

表10 车间改进成本层下的权重及总权重

表11 车间改进时间层下的权重及总权重

故W*=(0.027,0.085,0.047,0.101,0.049,0.073,0.132,0.239,0.068,0.047,0.021,0.031,0.080)

(2)计算客观权重

由4种方案的要素对比可以得到原始数据矩阵，需要将其中的模糊语言量化处理后方能进行数学运算，规定{一般，较好，好，非常好}={0.5,0.6,0.7,0.8}，{低，较低，一般，较高}={0.2,0.4,0.6,0.8}，由式(8)～式(10)可得到标准评价矩阵A：

由式(11)～式(13)可计算出评判依据：

η=(2.174,2.711,2.658,2.745,2.105,2.134,

2.172,2.473,2.672,3.205,2.153,2.095,2.325)

所以由式(14)可得客观权重：

U=(0.069,0.086,0.084,0.087,0.067,0.067,

0.069,0.078,0.084,0.101,0.068,0.066,0.074)

(3)叠加授权

由式(15)、式(16)进行叠加授权，可得到最终的权重：

V*=(0.050,0.082,0.065,0.090,0.056,0.067,

0.100,0.170,0.073,0.076,0.048,0.050,0.074)

4.2 各方案关联评价结果

标准化处理后，可得到规范矩阵：

规范矩阵不含权重因素，由式(18)，可得加权标准化矩阵：

在该矩阵中，每一行代表授权后各指标的标准化数量级，每一列表示每一个方案的各指标集。由式(19)、式(20)可得到正负理想点集：

P+=(0.0359,0.0498,0.0395,0.0165,0.0203,0.0407,

0.0405,0.1032,0.0318,0.0337,0.0221,0.0187,0.0287)

P-=(0.0154,0.0311,0.0246,0.0658,0.0365,0.0254,

0.0596,0.0644,0.0415,0.0432,0.0262,0.0327,0.0431)

由以上结果及式(21)～式(23)可计算出每个方案的各指标到最理想点的距离L+和最偏离点的距离L-，以及相对偏离度G。用G值大小对各方案进行综合评估，得到如下的计算结果表格。

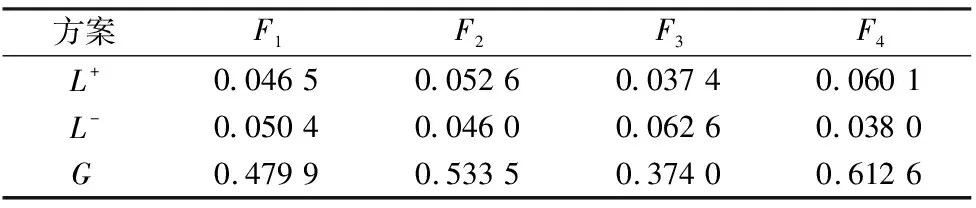
表12 各方案相对偏离度计算结果比较

对比表格数据，可得到相对偏离度的大小顺序为G3

5 结论

本文创新性建立了一套绿色制造车间优化改造方案的评价体系，从车间生产效能、环境友好度、生产质量、车间改进成本、车间改进时间五个方面对已有方案进行综合评估，充分考虑到了环境友好型要素及传统要素，在此基础上提出了把 TFN-AHP法和CRITIC法相结合进行叠加授权，并通过TOPSIS法加权量化指标的方案评价模型，相比经验评估而言，本文的方法克服了传统方法对经验依赖程度高，判断方式单一的缺点，更具有适普性和实用性，一套算法可解决多种情形下的制造车间改造方案优选问题。最后，用实例证明了该方法的可行性以及实用性，为解决车间优化问题提供了新的思路。