基于内共生算法的混装线平衡和排序协同优化*
2022-01-27张新敏
王 壮,张新敏
(沈阳工业大学机械工程学院,沈阳 110870)
0 引言
随着柔性更高的混流装配线在市场中得到更加广泛的应用,如何进行混流装配线的优化,成为急需解决的问题。平衡和排序是影响混流装配线的两个关键因素。这两个互相独立又紧密联系的因素共同决定了混流装配线的优劣,国内外学者也针对这两个问题进行了大量的研究。
大多数学者在对混流装配线进行优化时,单独的进行平衡或排序研究。针对平衡的研究主要分为两类:第一类是混流装配线初次平衡的静态研究[1-3];第二类是混流装配线再平衡的动态研究[4-5]。针对排序的研究主要分为三类:第一类是负载均衡问题的研究[6-7];第二类是生产平准化问题的研究[8-9];第三类是产品相似性问题的研究[10-11]。以上研究在优化过程中没有考虑到平衡和排序之间的相互影响,单独的考虑平衡和排序难以达到整体最优。
因此一些学者开始同时考虑平衡和排序,以求得混流装配线的整体最优。文献[12-13]以平衡方向的负载均衡等指标进行整体方案的评价,求得使整体最优的组合解。文献[14-15]以排序方向超载工作等指标,利用协同进化算法求得平衡和排序的最优组合方案。这些研究同时考虑平衡和排序两个因素,但评价指标偏向平衡或排序单个方面,不是对组合方案的整体评价,难以求得整体最优的问题没有得到很好解决。
本文在混流装配线优化的过程中,同时考虑平衡和排序两个因素,设计出平衡和排序组合方案的整体评价指标。以实际负载均衡和实际闲置时间最小为目标,构建混流装配线平衡和排序协同优化模型。对协同进化算法进行改进,设计出内共生进化算法进行模型的求解,求得的组合方案能使混流装配系统达到整体的最优。
1 混流装配线协同优化模型
1.1 参数定义

1.2 问题描述
混流装配线是在一条装配线上同时生产M个品种的产品,M个产品的总需求量为D,每种产品的需求量为Dm,各操作任务的时间和优先关系已知。混流装配线平衡问题的研究是通过综合优先关系,将多产品转换成单产品进行研究。混流装配线排序问题的研究是采用循环排序法,只对一个MPS中的产品排序,通过重复一定次数的排序循环,实现对所有产品的排序。混流装配线平衡和排序协同优化是在一定的资源限制下,对混流装配线系统的整体进行优化,在求解过程中利用平衡和排序之间的相互影响,同时进行平衡和排序问题的研究,求解出使混流装配线整体最优的平衡和排序的组合方案。
1.3 模型建立
混流装配线协同优化的关键的因素是组合方案评价指标的设计,优秀的评价指标能够快速地求出质量更高的解。传统的评价指标准主要是针对平衡或排序单方面进行设计,以应用最多的ADW(绝对负载偏差)为例,表达式如下:
(1)
(2)
(3)
由表达式可知,ADW在衡量负载偏差时以分配到各工作站操作任务的时间为基础进行计算,这个时间是理论上各工位的工作时间。在单独进行平衡研究时,可以将理论时间作为此工位的工作负载进行均衡优化。在实际中不同的排序方案会使各工位内产生不同的闲置时间,闲置时间虽然不是负载,但它会影响产品在工作站的停留时间,此时各工位内的实际工作时间和理论工作时间之间会存在偏差。在这种计算方式下各工位间的负载虽然均衡,但产品在各工作站的停留时间并不均衡,在实际生产中会造成各工位忙闲不均,长时间运行会产生在制品堆积等问题。
本文在进行组合方案评价指标的设计时,综合考虑平衡和排序之间的相互影响,以一个MPS内的各工作站内的工作时间和闲置时间之和为实际负载进行均衡优化。同时对闲置时间进行限制,避免闲置时间过多造成生产浪费。实际负载求解过程如下。
序列中第1个产品m1在工作站1开始和结束的时间:
Z11=0;
E11=Z11+Tm1,1
序列中第1个产品m1在工作站j的开始和结束时间:
Z1j=Z1,j-1+Tm1,j-1
E1j=Z1j+Tm1,j
序列中第s个产品ms在工作站1开始和结束的时间:
Zs1=Zs-1,1+Tms-1,1
Es1=Zs1+Tms,1
序列中第s个产品在第j个工作站中的开始和结束时间:
Zsj=max{Es,j-1,Es-1,j}
Esj=Zsj+Tms,j
实际负载是最后一个产品在某个工作站结束的时间,减去第一个产品在这个工作站开始的时间:ALj=ESj-Z1j。
目标函数:
(4)
f2=min(idtsj)
(5)
约束条件:
ALy=Esj-Z1j
(6)
(7)
(8)
(9)
(10)
(11)
Es,j+1-Tms,j+1≥Esj
(12)
Es-1,j-Tms-1,j≥Esj
(13)
式(4)、式(5)为目标函数,求最小的实际负载偏差和和最小的闲置时间;式(6)、式(7)是实际负载偏差和闲置时间的计算公式;式(8)保证一个任务只能分配到一个工作站;式(9)保证一个位置上只能安排一个产品;式(10)保证一个序列产品的总数目等于一个MPS中产品的总数目;式(11)保证各操作任务满足优先关系;式(12)保证产品只有在本工位加工完成后才能在下一个工位进行加工;式(13)保证在本工作站内只有加工完当前产品,才能进行下一个产品的加工。
2 内共生进化算法
内共生进化算法来自文献[16]提出的共生理论,是在协同进化算法的基础上进行改进。在内共生进化算法中存在两个或两个以上的种群,每个种群中的个体代表整体问题的部分解,不同种群中个体的相互组合,代表整个问题的完整解。该算法的显著特点是它保持了个体及其共生伙伴的结合。内共生的存在可以加速个体向好的解决方案收敛的速度。
2.1 算法的设计
在内共生进化算法中构建了3个种群:平衡种群(Pop-B)、排序种群(Pop-S)和组合种群(Pop-BS)。其中平衡和排序种群中的个体代表着任务分配方案和产品的排序方案,是问题的部分解。组合种群中的每个体是平衡和排序个体的组合体代表问题的完整解。在算法中存在两种进化机制:协同进化和内部竞争。种群Pop-B中的个体和种群Pop-S中的个体协同进化,并相互结合成新的组合种群Pop-BS’。新组合种群Pop-BS’和旧组合种群Pop-BS通过互换优秀的个体来淘汰种群内部低劣的个体,原组合种群中优秀的个体保持不变,算法示意如图1所示。
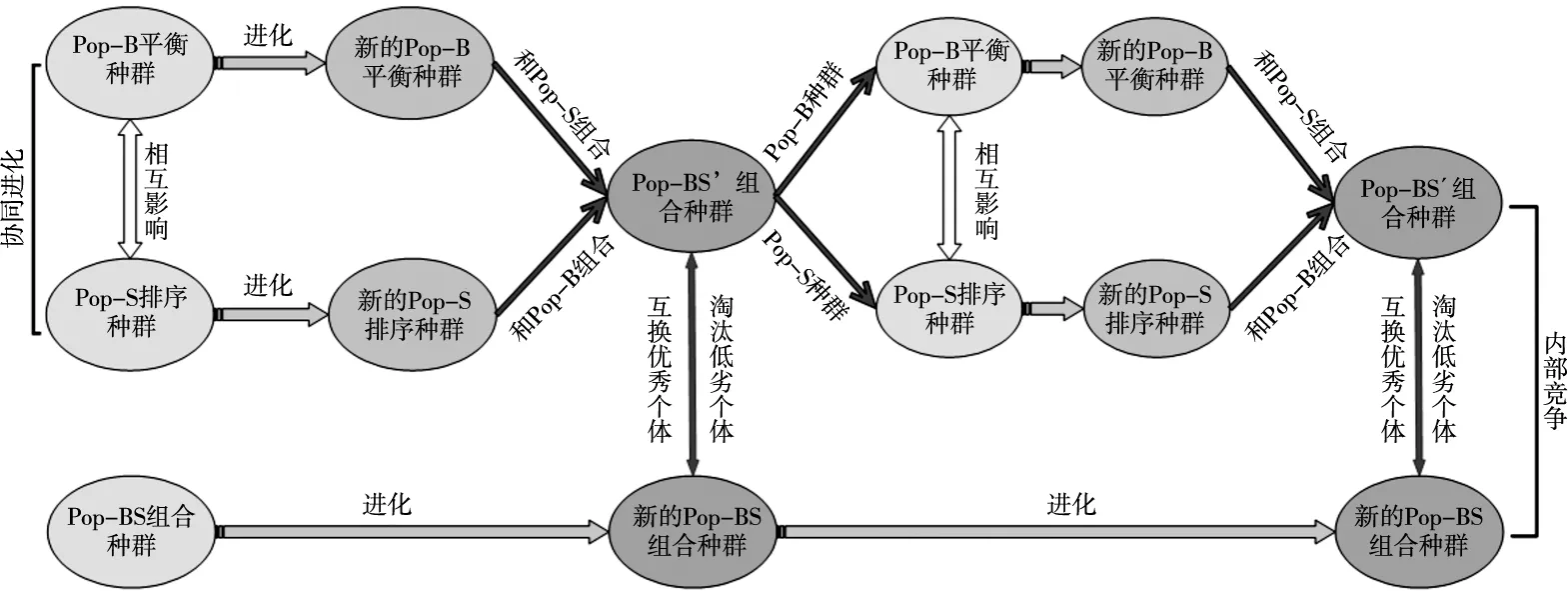
图1 内共生算法进化图
2.2 算法的流程
内共生进化算法的流程如下:
步骤1:种群初始化
①生成平衡和排序的初始种群Pop_B0和Pop_S0;
②由Pop_B0和Pop_S0结合生成组合种群的初始种群Pop_BS0。
步骤2:计算种群Pop-BS0的适应度,并保存适应度最大的个体Pop-BSbest0和最大适应度值fbest0(Pop_BS0);
步骤3:协同进化
①对平衡种群进行选择、交叉、变异操作生成新平衡种群Pop_B1;
②平衡种群Pop_B1中的所有个体和最佳组合个体Pop-BSbest0的排序部分进行组合生成新的组合种群Pop_BS1;
③计算新的组合种群Pop_BS1的适应度,求出适应度最大的个体Pop-BSbest1和最大适应度值fbest1(Pop_BS1);
④若fbest1(Pop_BS1)>fbest0(Pop_BS0),则更新最佳组合个体和最大适应度值;进行步骤⑤
⑤同理对排序种群进行①~④操作;
步骤4:内部竞争
①对组合种群Pop_BS0进行选择、交叉、变异操作生成新的组合种群Pop_BS3;
②交换组合种群Pop_BS3和步骤3中得到的组合种群Pop_BS1、Pop_BS2中优秀的个体以淘汰种群内部低劣的个体,原种群中用于交换的优秀的个体保持不变;
步骤5:若满足终止条件程序终止,否则转至步骤③。
2.3 算法进化操作
对于平衡和排序问题的遗传和进化操作的研究已经相当成熟,本文在前人的基础上重点研究组合个体的遗传表达和进化操作。以数字序列[1,5,3,4,2,6]代表平衡序列,字母序列[ABBACC]代表排序序列,组合序列的编码如图2所示。头部代表平衡序列尾部代表排序方案。
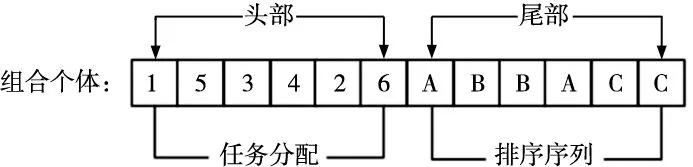
图2 组合个体表达方式
在染色体进化产生新的个体时,分两步进行:①先分别对头部和尾部进行交叉操作,生成新的个体;②分别对头部和尾部进行变异操作产生新的个体。这里针对头部和尾部进行的交叉和变异操作采用平衡和排序单个体一样的交叉和变异操作。
3 模型的求解与算法的验证
3.1 算例描述
为验证混流装配线平衡和排序协同优化模型和内共生进化算法的有效性,本文通过对Thomopoulos[17]问题的求解进行验证。在Thomopoulos问题中一个MPS中三种产品的比例为[3 2 1];三种产品的综合操作时间为[100 144 28 48 44 24 102 50 74 8 66 50 16 44 204 6 90 78 66];三种产品的综合优先关系如图3所示。
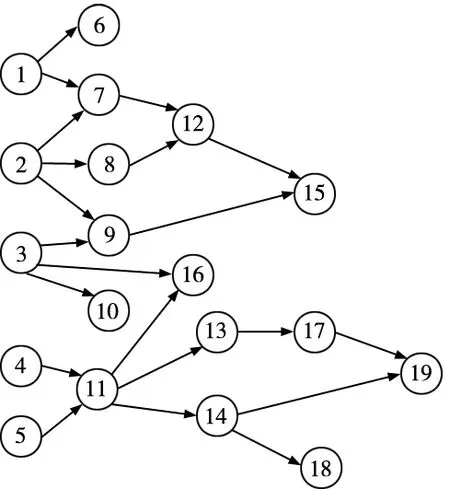
图3 Thomopoulos问题三种产品优先关系
以实际负载偏差和闲置时间最小为目标建立数学模型,分别采用遗传算法(GA)、协同进化算法(EA)和内共生进化算法(EAA)进行求解。
遗传算法采用传统串行的求解方式,先对混流装配线平衡问题进行求解,在已得平衡方案的基础上进行排序问题的求解,求得使整体最优的平衡和排序组合方案;协同进化算法采用并行求解方式,将整体解分成平衡和排序两个部分,求解时两个部分相互组合协同进化,求得使整体最优的组合解;内共生进化算法在协同进化算法中加入内共生体(平衡和排序组合个体),内共生种群和协同进化种群互换较好的个体,以淘汰中群内低劣的个体。
3.2 参数设置
平衡种群、排序种群和组合种群的初始规模都为100,变异率为0.8,交叉率为0.2,两个种群最优基因交换的数目为5,工作站数为3,迭代次数为500次。
3.3 结果对比
分别使用三种算法对Thomopoulos问题进行求解,三种算法求得的最佳组合方案如图4~图6所示。
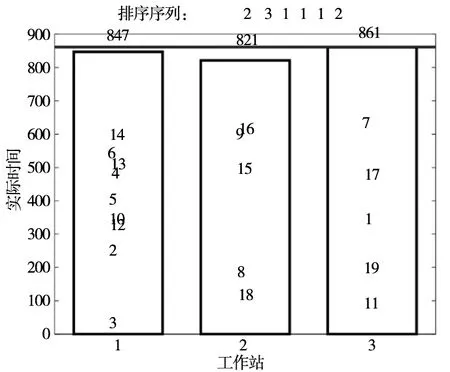
图4 EAA求解结果
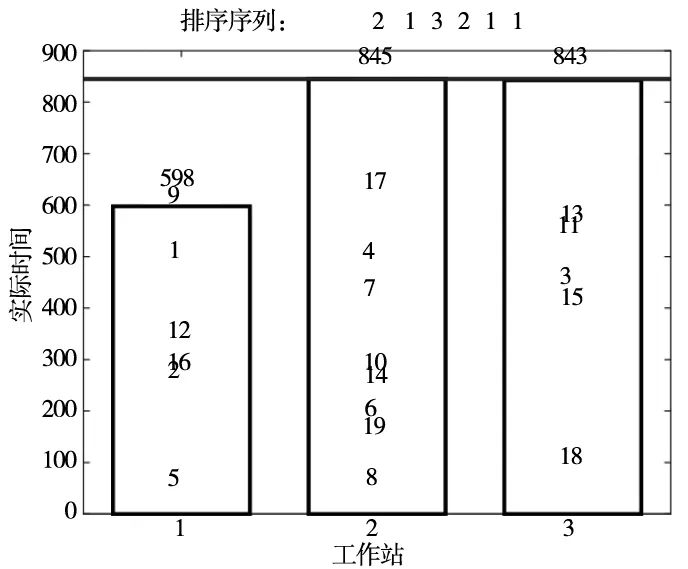
图5 EA求解结果
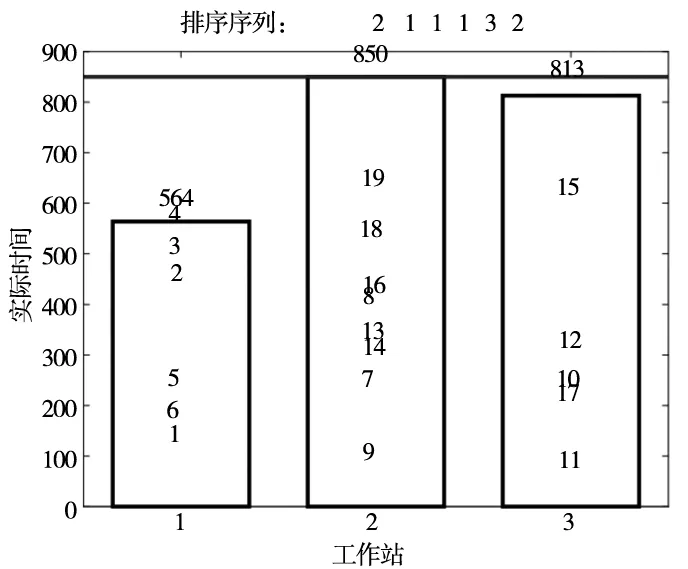
图6 GA求解结果
三种算法求解的目标函数值如表1所示。表中是每个算法运行10次目标函数的平均值,其中提升率是协同进化算法和内共生进化算法相对于遗传算法目标函数函数的提升,计算公式为:{(EEA-GA)/GA}×100%。

表1 三种算法求解结果
由结果可知:传统以串行的方式进行平衡和排序问题的求解结果最差,传统的串行求解思路只能求得平衡或排序的部分最优,无法求得平衡和排序的组合最优,并且传统算法在求解集成问题时,解的搜索效率和搜索能力较差。
在并行求解思路中内共生进化算法的求解结果最好,这说明与协同进化算法相比,内共生进化算法在求解过程中,通过不同种群间优秀内共生体的交换不仅能够加种群的多样性,避免算法早熟,而且还能够提升解的质量和求解效率。
如图7所示展示了目标函数随着迭代次数的收敛曲线,由收敛曲线可知内共生和协同进化算法相比于遗传算法,在寻优能力和收敛性方面的得到很大的提升。在三种算法中内共生进化算法的收敛速度最快,求解结果最好,在求解集成问题时具有更大的优势。
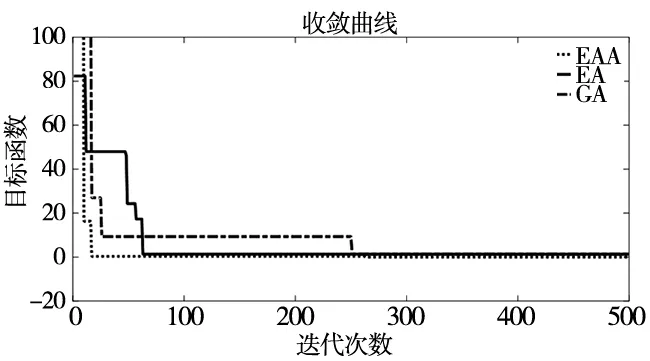
图7 三种算法收敛图
4 结束语
(1)对混流装配系统进行分析发现,传统串行求解方式和偏向性评价指标,无法综合考虑平衡和排序之间的联系,难以求得系统的整体最优方案;
(2)并行求解方式和综合性评价指标相结合的模型,能够弥补传统串行求解方式难以达到整体最优的缺陷;(3)通过算例验证了模型的可行性,并且内共生进化算法与另外两种算法相比,具有更佳的寻优能力和收敛性。
