例析常微分方程在数学建模中的应用

◎陈 杰

(苏州旅游与财经高等职业技术学校，江苏 苏州 215104)

一、引 言

在许多实际问题中，人们常常需要寻求变量之间的函数关系.有时这种关系无法直接建立起来，但是可以建立起该函数的导数所满足的关系式，这种关系式就是微分方程.微分方程是在处理实际问题中产生的，纵观微分方程的发展，它与物理、化学、医学、生物学以及天文学等方面都有着密切的联系，例如飞行器的运行轨迹，污染物浓度的变化，介质的传播，传染病的扩散与控制等都会用到微分方程的理论.

数学建模就是用数学的思想方法对复杂的现象进行分析，并用数学语言描述其中的关系或规律，抽象出恰当的函数关系，将实际问题转化成数学问题并加以解决.数学建模的过程就是一个分析问题、解决问题的创造性思维过程，也是一个演绎推理与归纳总结相结合的过程，对现实问题的观察、假设、归纳，怎么将其转化为一个数学问题是数学建模的关键.对于不同的问题可以用不同的方法来建立数学模型，如常见的运动变化率的问题可以利用导数知识来建立模型，常见的抽样调查问题可以利用统计学知识来建立模型，在研究买彩票中奖的概率的问题可以利用概率论相关知识来建立模型等.

二、常微分方程融入数学建模思想的措施

在日常的常微分方程教学中，教师首先要有意识地培养学生的数学模型思想，善于利用教材中的数学模型作为典型案例进行分析探索.同时在案例素材的选择上也可以紧紧围绕学生所学的专业或者是日常生活中最常见的问题，通过学生比较熟悉的案例素材引导学生产生对数学模型建构的认识与理解，让学生利用常微分方程这个工具去解决专业中或实际生活中的相关问题，这在一定程度上还可以激发学生学习的积极性.其次在日常的常微分方程教学中，教师要有意识地结合数学模型进行案例教学，培养学生将实际问题抽象化成数学模型.这样可以有效锻炼学生的数学建模思维能力，提高学生实际问题解决能力.最后教师可采用启发讨论式的教学方法并利用现代信息技术构建数学模型.在数学建模思想融入常微分方程过程中，要引导学生参与到数学建模的各个环节中来，并针对每个环节让学生展开讨论，充分发挥学生的能动性，培养学生自主发现问题并能分析问题、解决问题的能力.教师在教学中也要教会学生利用现代信息技术建立数学模型，这样可以让学生对数学建模有更直观的认识，同时也能简化模型建立过程中复杂的数值运算.

三、常微分方程在数学建模中的应用

数学建模是联系数学和实际问题的纽带，是数学在相关领域被广泛应用的媒介.数学建模的方法有很多种，而利用微分方程建立数学模型是其中重要的一种.常微分方程可以很好地将实际问题通过数学的语言进行转化，从而能有效地简化处理问题的过程，将问题解决.

利用常微分方程解决实际问题一般可按如下步骤进行：首先，用数学符号假设出实际问题中所涉及的变量和变化率，找出问题中包含的原理以及相关公式、定理等，根据问题的规律列出相应的微分方程；其次，对微分方程进行求解或对方程进行进一步的定性分析.对于参数问题模型需进一步讨论参数变化对于问题的影响；最后，对结果进行描述、分析、预测或控制.下面从日常生活、几何、物理以及经济等方面常见例子来介绍微分方程在数学建模中的广泛应用.

(一)日常生活方面的应用

日常生活中的很多问题都可以建立数学模型，并利用常微分方程进行解决.下面以日常交通出行中最常见的红绿灯问题以及生活中经常出现的溶液稀释问题为例，介绍常微分方程在数学建模中的应用.

例1(红绿灯问题)：在一些大城市中，由于汽车保有量比较大，等红绿灯时的拥堵一直是一个比较麻烦的问题.在红绿灯转换的过程中通常会有个过渡状态的黄灯.怎么合理的设置红绿灯的时间，即能保证交通安全又能避免由于车辆积压造成等候时间过长，给司机和乘客造成烦恼，如何设置黄灯闪烁的时长，是交通指挥灯经常要处理的问题.

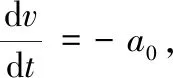
例2(溶液稀释问题)：假设现有一批工业盐溶液，每升溶液中含0.3 kg的工业盐，现以2 L/min的速度将溶液倒入装有10 L纯净水的容器中，溶液在容器里经过稀释后又以相同的速度从容器中流出，问经过5 min后，容器中还剩有多少工业盐.

解：令时间t为函数的自变量，把注入容器经过t分钟时工业盐的数量看作待求解的未知函数y(t)，接下来求t到t+Δt这段时间间隔内工业盐的变化量.

流入：2ΔtL溶液中含有0.3·2Δt=0.6Δtkg的工业盐.

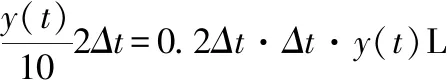
于是，在这段时间内工业盐的增量为y(t+Δt)-y(t)=0.6(Δt-0.2)Δt(y(t)+α)，上式除以Δt，当Δt→0时求极限，可得微分方程y′(t)=0.6-0.2y(t).

求通解得y(t)=3+Ce-0.2t，而y(0)=0，代入上式求得特解为y(t)=3-3e-0.2t.

所以，当t=5时，容器中将有y(5)=3-3e-0.2×5=3e-1≈1.9 kg的工业盐.

在上例中主要体现了数学建模的思想，在实例中，引入了时间变量，建立了微分方程模型，通过求其特解，进而求得其结果.

(二)几何方面的应用

常微分方程还可建立求解几何问题的数学模型，主要利用导数的几何意义，即函数y=f(x)的导数y′等于函数所表示曲线上点(x,f(x))处切线的斜率.

例1已知一条曲线通过点(1,3)，且曲线上任何一点(x,y)处切线介于x轴及y=x+1之间的线段正好被切点所平分，求该曲线的方程.

解：设该曲线的表示式为y=y(x)，则过任意点(x,y)的切线方程可表示为：

Y-y=y′(X-x)

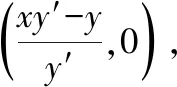
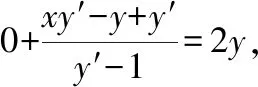
这是一个一阶线性方程，通过计算可得曲线的方程为：

y2-xy-y=3.

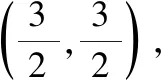
解：设点N的坐标为(x,y)，则切线NA的方程为Y-y=y′(X-x).令X=0，则Y=y-xy′，故点A的坐标为(0,y-xy′).

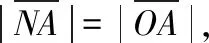
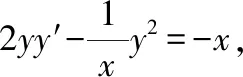
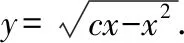
(三)物理方面的应用

微分方程物理应用的范围很广，几乎涉及物理学的每个分支，但应用得较多的领域是动力学及电学.在动力学中主要用牛顿第二定律，在电路分析中主要用克西霍夫定律.

例1从地球表面垂直向上发射一枚质量为m的火箭，考虑火箭所受空气阻力可忽略不计的理想状态，设火箭初速为v0，求火箭能克服地球引力发射到无穷远去的最小速度.

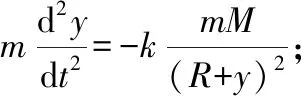
这时一个形如y″=f(y,y′)不显含自变量的二阶微分方程，可降阶为一阶微分方程.

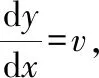
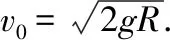
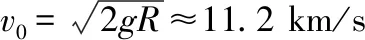
例2在RLC串联电路中串接交流电源E0sinωt，求回路电流i(t).

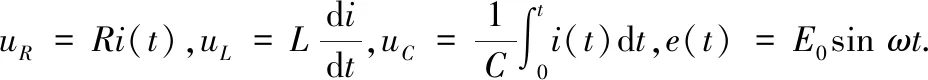
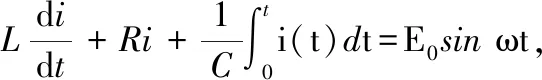
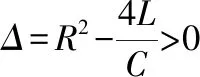
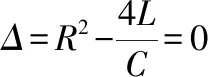
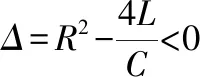
当ω≠ω0时，非齐次方程(1)的通解为

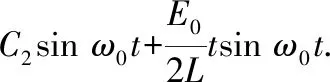
由解得结果分析可知，当ω≠ω0时，回路电流i(t)是一个周期振荡的电流；当ω=ω0时，由于特解中含有tsinω0t项，当t→∞时振幅可趋于无穷，这就是共振现象.

(四)经济学方面的应用

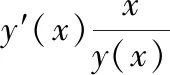
例1(人口模型)某城市在时刻t的人口函数用p=p(t)表示，m及n分别表示该城市的出生率和死亡率，在时间段Δt内出生人口与死亡人口都与Δt成正比.求在不发生意外的情况下，该城市的人口函数.

解：考虑在时间段[t,Δt]内人口的变化：(m-n)应表示人口的自然增长率，一方面，(m-n)p(t)Δt应近似表示这个时间段内人口的变化；另一方面，Δp=p(t+Δt)-p(t)精确表示了这个时间段内人口的变化，由此Δp≈(m-n)p(t)Δt.

注：生物群体的生灭变化是一个随机过程，本例给出的只是一个简化的近似模型.

例2(房贷模型)某客户向银行申请住房贷款，贷款本金为y0=20万元，贷款月利率为λ=0.0045，协议贷款时间为300个月，问该客户平均每月应向银行还贷本息为多少.(银行利息需计复利)

解：记y(k)为第k个月还款后尚欠银行的本息数，x为每月还贷金额(为常数)，则可建立方程y(k+1)=(1+λ)y(k)-x，初始条件为y(0)=y0，这时线性差分方程的初值问题：

通过求解可得x=1216.26元.

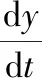
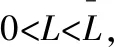
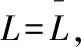
四、结束语

常微分方程在数学建模中的广泛应用，将数学理论方法与实际生活巧妙地结合了起来，将生产生活实际中不容易解决的难题用数学的方法解决.常微分方程建立起来的数学模型，一般都是动态的数学模型，虽然整个推导过程相当复杂，但是结果却是简单明了.因此，将常微分方程和数学建模有机结合起来，能够让常微分方程在实际应用过程中发挥更大的作用，解决更多的实际问题.