基于信息技术环境培养学生几何直观能力的“五化”策略

◎林传忠

(福建省厦门市湖里区教师进修学校,福建 厦门 361009)

前 言

信息技术已成为当今社会经济、科技发展的最重要的工具，并影响着社会的各个方面.信息技术飞速发展对教育产生了重大的影响，因为信息技术为教育教学提供了一个全新的平台，它作为一种新的媒介加入课堂教学，弥补了传统教育中的众多不足，改变了传统的知识存储、传播和提取的方式，实现了大量信息的呈现，以其互动性、直观性、动态性，为课堂教学的有效实施提供了更形象的表达工具，有效地激发了学生的学习兴趣.在教学中，教师要基于计算机技术、多媒体技术和网络通信技术等信息技术为主的教育应用技术环境，通过信息技术手段，变抽象为具体，变静止为动态，引导学生参与学习过程，从而有效地提高教学效率.

数学学习是一个较为抽象的过程，如果没有直观形象动态的信息融入，那么必将是枯燥乏味的.小学生的思维以形象思维为主，而数学学习却是抽象的，这便形成了矛盾，如何更好地解决这个矛盾？那就是要把数学学习建立在可接受的直观形象的载体上，培养学生的几何直观能力是一种很好的方式.《义务教育数学课程标准(2011年版)》指出几何直观主要是利用图形描绘和分析问题，几何直观可以把复杂的数学问题变得简明，有助于学生探索解决问题的思路、预测结果[1].几何直观可以帮助学生直观地理解数学知识，而且能够发展学生的创造性思维，在整个数学学习过程中发挥着重要作用.几何直观能力是人们利用实物、模型和图形，生动形象地描绘数学问题，直观地反映和揭示解题思路，从而有效解决数学问题的一种认知能力.良好的几何直观能力是学生学好数学的基本能力.正如弗莱登塔尔所说：“几何直观能告诉我们什么是可能重要、可能有意义和可接近的,并使我们在课题、概念与方法的荒漠之中免于陷入歧途之苦.”培养学生几何直观能力是数学教学的重要任务之一.信息技术可以把数学知识的抽象性转化为具体的事物及可见的过程，有助于学生几何直观能力的形成与发展.

笔者经过实践得出基于信息技术环境培养学生几何直观能力的化静为动、化表为里、化隐为显、化抽象为具体、化思考为表达的“五化”策略，能较好地培养学生几何直观能力.

一、化静为动

信息技术的特点之一就是动态性.借助微课、电子画板等技术可以将静止的教学内容变成动态的过程，在思维呈现上更具连贯性，能动态地把思考过程表达出来，这些具体的动态过程必定会在学生脑海中留下深刻的表象，从而为学生几何直观能力的发展奠定基础.

例如，在人教版六年级上册“圆的面积”一课之后，有这样的一道题：在公园里有一个自动旋转喷灌装置，射程为5 m，这个自动旋转喷灌装置能浇灌多大的面积？虽然教师也会通过画图的方式来呈现题目，但效果并不太理解.这时，教师便可利用电子画板，把浇灌的过程动态地呈现出来，学生脑海中就形成了浇灌面积的表象，就很直观形象地理解了题目的意思.又如，人教版五年级下册“长方体的表面积”一课，学生对于长方体的表面展开图很难理解，因为这需要学生有很强的空间观念.为此，教师可以利用电子画板，通过生、机互动的方式把长方体的各种表面展开图一一呈现出来，学生在操作与观看的过程中，自然就有充分的思维印象及体验，这为形成长方体的表面展开图的空间表象提供了强有力的直观形象背景，同时，在学生操作与观看之后，让学生把长方体表面展开的过程在脑海中回想一遍，会使学生对长方体的表面展开图的理解更加深刻.

学生观看微课、电子画板时，自然会在脑海中留下深刻的表象，在此基础上，教师让学生在脑中回想微课、电子画板呈现的动态过程，基于微课、电子画板的动态呈现，以及学生的自主想象，学生对所学内容的理解便会很具象且有厚度，进而逐渐摆脱实物直观和影像直观，进行更高层面的想象直观.

二、化表为里

数学知识内在的逻辑性，不仅体现为知识螺旋上升的关系，还体现为数学本质上的联系.理解这些联系是学好数学的根本，但学生对于数学本质的理解是有难度的，这时，教师便可借助微课、电子画板等信息技术手段，化表为里，把知识内在的联系呈现出来，让学生能形象直观地透过现象看到本质，从而促进学生几何直观能力的提升.

图1

又如，在教学人教版三年级上册“时 分 秒”一课时，学生对于一天24时，时针在钟面上要旋转两圈，钟面上1时的位置既表示1时，又表示13时等感到困惑.时间这个概念极具抽象性，对于三年级学生来说，理解起来难度还是很大的.这时，教师可以借助信息技术手段，先呈现时针在钟面旋转两周的动态过程，让学生感受一天时针要在钟面上旋转两圈，然后呈现时针在钟面上旋转一圈的过程，并把这一旋转的过程转化为如下线段(如图2):

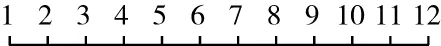
图2

时针在钟面上旋转第二圈，把这一过程转化为线段，如图3：

图3

连接起来，如图4.

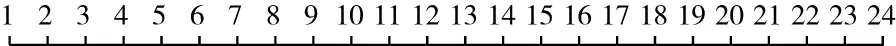
图4

学生对于线段是很熟悉的.借助线段，学生不仅理解了时针旋转两圈的过程，也理解了时针旋转第二圈时，实质上就是在12时之后增加的，第二圈钟面的1时就是12时之后的13时.通过以上过程，学生就能透过钟面的圆形的表象，理解一天24时时针在钟面上旋转两圈的过程，实质上与在两条线段上走的过程是一样的，只是在钟面呈现出的是不断旋转的过程，而在线上是不断延伸的过程.在此基础上，教师可以让学生把这个过程画下来，增强学生的几何直观表象，从而促进学生几何直观能力的发展.

通过信息技术手段，化表为里，引导学生感受几何直观思想的重要作用，并通过运用几何直观思想理解知识的本质.

三、化隐为显

徐利治先生提出：“直观就是借助经验、观察、测试或类比联想,所产生的对事物关系直接的感知与认识，而几何直观是借助见到的或想到的几何图形的形象关系产生对数量关系的直接感知[2].”数学知识中有许多抽象概念，例如吨、公顷、平方千米等，由于这些概念离学生的实际生活太远或受学生现阶段思维的限制，学生只能根据计量单位之间的进率类比迁移，这对于一部分学生来说，是很抽象的，理解起来是很困难的.这时，教师就要借助学生已有的生活经验与知识基础，通过信息技术手段把这些隐性的知识与学生已有的显性知识结合起来，化隐为显，使学生更好地掌握知识.具体地，在教学“吨”这个概念时，教师可以通过信息技术把“吨”与“千克”建立联系，小学生对于“千克”是有感受的，先让学生抱一下20千克的矿泉水，再通过微课动态地画出50个矿泉水桶，学生有了体验参照，理解“吨”的概念就容易多了.

又如，在教学人教版五年级下册“观察物体”时，几个小正方体重叠在一起，有部分小正方体隐藏在里面，无法直接看到.为了让学生更好地从前面、后面、左面、右面、上面等方向观察到物体的情况，教师可以通过摆出实物来让学生观察，但这种方法很有局限性，观察时必须完全与实物正对面，只有这样，才能看出正确的图形，但这却很难做到，并且能同时参与观察的人很少.因此，教师可以通过多媒体手段在物体的前面、后面、左面、右面、上面等方向呈现图形，这样，学生就可以直观地看到不同位置上的图形.在学生观察物体的各个方面的同时，让学生画出图形，然后闭上眼睛想象出完整的物体，从而发展学生的空间想象能力.

数学知识是存在密切联系的.数学知识的发展总是从具体走向抽象.所以越后面的知识，对于学生来说，隐蔽性就越强，学生理解起来就越困难.借助信息技术，直观地把新知识与旧知建立联系，通过旧知识与新知识的对比，化隐为显，能够帮助学生理解新知，并形成几何直观能力，进而促进思维发展.

四、化抽象为具体

又如，一根圆形水管，从里面量，水管的直径是20 cm，水管内水流速度是1.5 m/s，那么每分钟从这根水管流过的水的体积是多少立方米？学生对水流动的过程无法把握.这时，教师可通过多媒体手段，先呈现动态的水管流水过程，然后以水管某个点为起点，水流经过1分钟时确定终点，截图如图5.这样就把学生无法把握的隐性流水过程变成了可观可感的显性圆柱体，学生就能直观地理解题意，进而解决问题.

图5

信息技术能还原事件的过程，化抽象为具体，让过程看得见.有过程的支撑，学生几何直观能力的形成就有了具体可感的背景，这有利于学生几何直观能力的发展.

五、化思考为表达

数学语言有三种基本形态：文字语言、符号语言、图形语言.学生的数学思维就是在这三种语言的相互转化中得到发展的.图形语言表达能力的培养的意义在于能让学生将文字语言所表达的内容用图形语言表达出来.微课、电子画板能将数学内容表达得更加具体生动，不仅能促进学生对内容的理解，还能促进学生图形语言的积累，发展学生用图形语言解决问题的能力，发展学生几何直观能力.

例如，在教学人教版五年级上册“平行四边形面积计算”一课时，在学生独立思考、小组交流之后，教师可以通过微课把平行四边形面积计算公式的推导过程连贯地播放一遍，给学生以强烈的直观感受，并在此基础上，引导学生通过“说”与“画”来表达过程：一是“说”过程.让学生把微课中图形转化的过程用语言表达出来，阐述图形转化过程背后的知识，进而提高学生识图的能力；二是“画”图形.在理解推导过程的基础上，引导学生将平行四边形面积公式的推导过程用图形画出来，再通过图形语言直观地表达出来，进而提升学生运用几何直观解决问题的能力.

运用信息技术培养学生几何直观能力，要建立在学生独立思考与实践的基础上，再通过微课、电子画板等信息技术手段进行呈现，这样呈现的内容才能与学生已有的知识结构建立联系.建构主义认为学生的学习是一个积极主动的建构过程.只有找到新知与旧知的联接点，新知才能通过同化或顺应进入到学生已有的结构之中.要形成和发展学生的几何直观能力，关键是要让学生的思维动起来，而信息技术只能起到强化和推进的作用.所以，基于信息技术培养学生的几何直观能力，首先要让学生运用已有的几何直观水平去呈现内容，暴露几何直观水平或存在的困惑，明确学习的方向，然后通过微课或电子画板进行呈现，这样，学生就会基于自己的情况进行有针对性的学习，调整重组已有的空间表象.在此基础上，教师要给学生再一次运用几何直观表示内容的机会，只有经过思考——演示——训练的过程，学生才能真正地形成几何直观能力.

结束语

几何直观是揭示现代数学本质的有力工具，有助于形成科学正确的世界观和方法论.由此可见，几何直观是学生思考、分析、解决问题的重要手段，它不仅在空间与图形领域发挥着重要作用，而且在数与代数、统计与概率、实践与综合应用等方面都有着重要的作用.信息技术的动态性、过程性、形象性能为学生几何直观能力的形成与发展提供强有力的手段支撑，能让枯燥、抽象的数学知识转化为内容可观可感、思维可见可说的数学知识.在教学中，教师要不断探索信息技术与几何直观能力的结合方式，促进学生几何直观能力的发展，更好地提升与发展学生的数学核心素养.