考虑时延和辟谣效应的谣言传播模型

裴 蕾，高彦平，刘新亮，宋绍义

(北京工商大学 电商与物流学院，北京 100048) (农产品质量安全追溯技术及应用国家工程实验室，北京 100048)

1 引 言

网络谣言，是指通过信息网络介质对公众关心的社会事物、事件或问题进行未经证实的表述或诠释[1].随着移动网络和应用的快速发展，网络用户的数量急剧增长，将网络谣言传播带入了一个新的媒体时代.互联网用户主要通过移动通信应用程序获取突发事件等信息，借助灵活的网络沟通，谣言传播速度变得更快，影响力更大[2-4].因网络谣言传播途径多、传播成本低等特点极易形成蝴蝶效应，对公共利益的杀伤力呈现几何级的增长.因此，研究社交网络中的谣言传播动态，建立有效的谣言传播模型，对有效控制谣言传播具有重要意义[5].

谣言在网络中的传播与疾病在人群中的扩散具有相似的规律，分析网络谣言传播的模型大多是基于传染病动力学模型的理论与方法[6-9].谣言传播模型可以用来描述突发事件下的公众恐慌，网络核爆式营销，流行病等多种社会现象.关于谣言传播模型的研究始于1965年Daley等人[10]提出的DK模型.但是谣言传播与疾病传播由于传播机制、传播途径的不同又存在一定的差异，此后，为了更准确地刻画谣言的动态行为和传播特征，研究者通过改进传统的传染病模型，在用户状态的多样性，用户行为的差异性，外界环境的扰动性，传播机制的独特性等方面做了大量的研究.Zhu等人[11]提出了增加两个离散时滞和Logistic增长的谣言传播模型，讨论了六种不同情形下正平衡点的局部稳定性.王宏波[12]在SIR模型基础上引入评价节点E和转发并评价节点IE，构建了信息传播演化模型，探讨了策略摇摆度等因素对信息传播的影响.Liu等人[13]提出了具有犹豫机制的SEIR模型，利用单调迭代技术证明了谣言盛行均衡的全局吸引性，得出谣言的高吸引力和模糊性有助于谣言的传播.Jiang等人[14]在SIR模型基础上引入积极传播节点P和消极传播节点N，建立了SPNR模型，以探索突发新闻的发展过程.Li等人[15]在SIR模型基础上引入联系状态C，表示用户已经从邻居节点获取了信息，但尚未决定是否传播，建立了SCIR模型错误!未找到引用源..Zhao等人[16]探讨了权威媒体、谣言传播与突发事件演变之间的相互作用机制.Li等人[17]探讨了政府的惩罚力度如何影响谣言的传播.张亚明等人[18]考虑到个体做出决策前，会受到外界两类对立观点的叠加影响，探究了双重社会强化对谣言传播的影响.王治莹等人[19]从交互传播整体视角出发，探究了政府实施不同干预措施对舆情信息传播的影响.学者们将这些差异分别定性为独立的机制融入到谣言传播模型中，Wang等人[20]通过引入无知节点与传播节点之间的信任机制，探究该机制对谣言传播的影响.Chen等人[21]建立了具有对抗机制的谣言传播模型，利用平均场理论，研究了谣言的传播动力学.Xu等人[22]引入了强化机制来描述个体传播谣言的意愿，引入多个中间状态来描述个体的扩散意愿逐步增强的过程，探究强化机制对谣言传播的影响.Wang等人[23]考虑谣言传播过程中人们遗忘和失去兴趣的现实，引入遗忘-回忆机制和兴趣衰减机制，构建了一种新型SIR模型.随着研究的深入，传播模型中节点的种类、节点转化规则、传播影响因素等逐渐趋于复杂[24-27].

综上所述，现有模型的局限性在于节点状态划分粗糙，状态转移规则不清晰，大多从单个角度出发，没有考虑用户和移动设备之间的交互对网络谣言传播的影响，并假设谣言在一个封闭的系统中传播，片面分析影响谣言传播的因素.而如今，人们主要通过移动社交平台获取最新信息，社交平台是一个开放的平台，随时都有用户注册或注销社交应用程序的社交账号，应考虑用户的迁入率和迁出率等人口动态因素；并且谣言传播过程受多方面因素的影响，有必要从不同方面研究谣言传播动力学机制.

本文从节点种类划分、外部社会影响以及用户行为差异等角度出发研究社交网络上的谣言传播.针对节点种类的划分，本文基于SEIR模型，引入了辟谣者的角色，表示在谣言传播过程中，有政府、媒体或公众积极辟谣的情况；在外部社会影响方面，结合信息受众感知视角和传播主体行为视角，引入辟谣信息可信度和辟谣者的辟谣力度建立辟谣机制；在用户行为差异方面，基于用户登录移动应用程序的频率不同，考虑用户和移动设备之间的交互，引入时延机制表示离线状态的未知者浏览信息存在延迟的情况.本文的第2节根据节点转化规则建立了社交网络谣言传播UETDR模型，并推导出相应的动力学方程.第3节讨论了模型平衡点的存在性和稳定性，并得出了基本再生数的表达式.第4节通过数值仿真实验，探究辟谣机制和时延机制对谣言传播过程的影响，并将本文提出的模型与传统的SIR模型、SEIR模型进行对比.第5节根据实验结果得出结论，给出一些控制谣言传播的建议.

2 谣言传播模型

本文将针对未知者中的离线状态节点接收信息存在延迟的情况，提出时延机制；针对辟谣信息可信度和辟谣者的辟谣力度存在差异的特点，提出辟谣机制.在传统传染病模型的基础上，结合复杂网络传播动力学理论，提出改进的UETDR模型.根据用户接受信息的心理变化和行为反应，将网络中的节点分为5类状态，如表1所示.

表1 不同类型节点的具体含义
Table 1 Specific meaning of different types of nodes

节点节点名称节点含义U未知者指用户的移动社交设备没有接收到谣言,包括在网络中处于在线状态和离线状态的节点用户E潜伏者指处于离线状态的用户的移动社交设备已经接收到谣言,但由于用户还未登录社交平台,尚未阅读到谣言,从而由未知状态转化为潜伏状态T传谣者指已经阅读过谣言并相信谣言,对该谣言做出传播决定的节点用户D辟谣者指已经阅读过谣言,但对谣言持反对态度并进行辟谣操作的节点用户R免疫者指用户阅读谣言后,U节点和E节点拒绝传播谣言,T节点和D节点对谣言不再感兴趣转化为免疫者的一类节点用户

本文提出的辟谣机制和时延机制定义如下：

1)辟谣机制

辟谣信息可以抑制谣言在社交网络中的快速传播[28，29]，在社交平台上，从信息受众感知视角出发，由于传播成本低，辟谣信息发布渠道多，并且针对虚假的信息缺乏严格的惩罚制度，导致部分用户对辟谣信息的真实性持怀疑态度[30].从传播主体行为视角出发，公众更倾向于相信高影响力用户发布的信息[31].因此辟谣信息可信度和辟谣者个体影响力是影响辟谣效果的重要因素，本文将同时从信息受众感知视角和传播主体行为视角出发，基于辟谣信息的可信度和辟谣者个体影响力，建立辟谣机制.通过引入辟谣函数刻画辟谣机制对谣言传播过程的影响，建立的辟谣函数如公式(1)所示：

(1)

其中f表示权重系数，λ表示初始传播概率，a表示辟谣信息可信度，b表示辟谣者个体影响力因子.用α1，α2，α3分别表示未知者、潜伏者和传谣者节点转化为辟谣者节点的概率函数，如公式(2)所示：

(2)

2)时延机制

网络中的未知者节点U分为在线和离线两种状态，在线时，未知者在收到信息后会迅速完成节点状态的转换.离线时，未知者节点无法实时接收信息，会首先转化为潜伏者节点E，并潜伏一段时间1/k，然后分别以kβ2、kα2、kε的概率转化为传谣者、辟谣者、免疫者，以此完成节点状态的转换.

在UETDR模型中，基于时延机制和辟谣机制定义节点的转化规则如下：

1)新加入网络的节点用户以恒定的比率δ成为网络中的未知者；

2)处于在线状态的未知者中以β1的概率转化为传谣者；考虑到时延机制，处于离线状态的未知者以概率θ转化为潜伏者.用户在阅读到谣言后，可能对谣言并不感兴趣，因此未知者、传谣者、辟谣者会以概率ε转化为免疫者；

3)受辟谣机制的影响，未知者、传谣者分别以概率α1、α3转化为辟谣者；

4)设定潜伏者的潜伏时间为1/k，单位时间内潜伏者分别以kβ2、kα2、kε的概率转化为传谣者、辟谣者、免疫者；

5)免疫者会逐渐忘记接收到的信息，以遗忘率γ重新转化为未知者；

6)随着时间的推移，网络中的每个节点用户以概率μ移出传播网络.

由上述转化规则得出，在单位时间内，U节点密度变化为δ-(θ+α1+β1+ε)U(t)T(t)+γR(t)-μU(t)；E节点密度变化为θU(t)T(t)-k(α2+β2+ε)E(t)-μE(t)；T节点密度变化为β1U(t)T(t)+kβ2E(t)-(ε+α3)T(t)-μT(t)；D节点密度变化为α1U(t)T(t)+α3T(t)+kα2E(t)-εD(t)-μD(t)；R节点密度变化为εU(t)T(t)+kεE(t)+εT(t)+εD(t)-γR(t)-μR(t).得出谣言传播模型的节点状态转移图如图1所示.

图1 UETDR模型示意图Fig.1 Schematic diagram of UETDR model

根据图1建立该模型的微分动力学方程，得到系统(3)：

(3)

其中U(t)，E(t)，T(t)，D(t)，R(t)分别表示未知者、潜伏者、传谣者、辟谣者、以及免疫者在t时刻的密度.其中t>0，状态间的转化概率均在[0，1]之间，系统(3)的初始条件满足U(t)≥0，E(t)≥0，T(t)≥0，D(t)≥0，R(t)≥0.根据系统(3)可知，状态转移概率α1，α2，α3展开后均可表示成初始传播概率λ、权重系数f、辟谣信息可信度a和辟谣者辟谣个体影响力b的函数，因此，为了简化计算未对α1，α2，α3进行展开.

3 系统平衡点及稳定性分析

本节将计算网络谣言传播模型的平衡点和基本再生数，并运用Routh-Hurwitz判据[32]讨论谣言传播平衡状态的稳定性.

3.1 系统平衡点与基本再生数

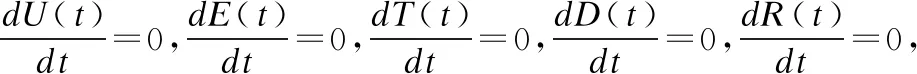
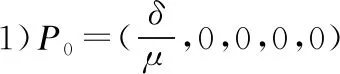
m1=(μ+γ)(μ+ε)(δβ1m2-μm2(μ+ε+a3)+δkβ2θ)

m2=k(α2+β2+ε)+μ

m3=μ(ε+μ+γ)(α1+β1+θ)+με(ε+μ)

借鉴传播学基本再生数的定义[33]，定义谣言传播模型的基本再生数为一个谣言传播者在传播过程中使得谣言未知者转变为谣言传播者的个数，是衡量谣言传播的感染能力的重要参数.R0=1为谣言传播阈值，当R0<1时，谣言不会形成扩散趋势，最终会消失在网络中；当R0>1时，谣言传播会在一定范围内形成扩散趋势.根据Driessche和Al-Darabsah采用的再生矩阵谱半径法[34，35]，计算基本再生数R0.令x=(T(t)，D(t)，R(t)，U(t)，E(t))′，将谣言传播模型(3)改写为：

(4)

其中:

矩阵φ(x)与矩阵ψ(x)在P0处的雅可比矩阵分别为：

其中:

可得FV-1的谱半径为：

3.2 无谣言平衡点稳定性分析

定理1.当R0<1时，系统(3)的无谣言平衡点P0是局部渐进稳定的.

证明：系统(3)中每个微分方程的右端分别对每个状态变量求导，得到五行五列的矩阵，再将平衡点P0代入到该矩阵中，即得到系统(3)在无谣言传播平衡点P0处的雅可比矩阵[36]：

求得特征值如下：

λ1=-μ

λ2=-μ-ε

λ3=-μ-γ

λ4=-(m4-δβ1+μ(α3+μ+ε)+μ(kβ2+μ+ε))

λ5=δβ1-μ(α3+μ+ε)+m4

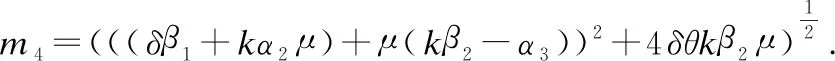
通过计算，当R0<1时，所有特征值都小于0，即所有特征值均有负实部.根据Routh-Hurwitz判别条件可得，无谣言平衡点P0是局部渐进稳定的，定理1得证.

3.3 有谣言平衡点稳定性分析

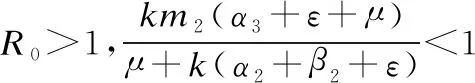
证明：系统(3)在有谣言传播平衡点P1处的雅可比矩阵为：

令:

g3=μ+k(α2+β2+ε)

令:

将Δi(i=1，2，3，4，5)定义为M2的i阶顺序主子式，则:

Δ1=|g1|=g1

由g1>0，g3>0可得Δ1>0，Δ2>0.

4 仿真实验与分析

本节将在理论分析的基础上，通过数值仿真实验进一步验证理论结果的正确性.并探究辟谣机制和时延机制对谣言传播的影响，最后将本文提出的UETDR模型与传统的SIR模型、SEIR模型进行对比，验证本文模型的有效性.

4.1 模型平衡点仿真分析

实验1.通过数值仿真实验证明无谣言平衡点P0是局部稳定的.

设定系统初始值U(0)=0.95，E(0)=0，T(0)=0.05，D(0)=0，R(0)=0，选取两组不同的参数，即δ=0.015，μ=0.016，α1=α2=0.2，α3=0.15，β1=β2=0.3，γ=0.6，k=0.9，θ=0.3，ε=0.2；δ=0.015，μ=0.016，α1=α2=0.2，α3=0.3，β1=β2=0.2，γ=0.6，k=0.9，θ=0.3，ε=0.25.图2和图3给出了两组R0<1时，5类节点密度随时间变化的情况.

图2和图3对应的R0值分别为0.78、0.33，系统的局部稳定点均为(0.942，0，0，0，0)，在这两种情况下，U节点的比例接近1，E、T、D、R节点的比例趋于0，结果表明，当R0<1时，谣言不会形成扩散趋势，谣言最终会消失.图2中T节点密度在t=5.9时趋于0，图3中T节点密度在t=4.1时趋于0.对比说明随着R0取值的减小，虽然各类节点的整体变化趋势保持一致，但T节点密度降低的速度加快，T节点密度更快地接近0，这表明可以通过减小R0的值，缩短谣言在网络中存在的时间.

图2 R0=0.78时的无谣言状态图Fig.2 No rumor state diagram when R0=0.78

图3 R0=0.33时的无谣言状态图Fig.3 No rumor state diagram when R0=0.33

实验2.通过数值仿真实验证明有谣言平衡点P1是局部稳定的.

系统初始值的设定与实验1保持一致，选取两组不同的参数，即δ=μ=0.01，α1=α2=0.25，α3=ε=0.15，k=β1=0.6，β2=γ=0.2，θ=0.3；δ=μ=0.015，α1=α2=0.2，α3=ε=0.25，k=β1=0.6，β2=γ=0.3，θ=0.35.

图4 R0=1.93时的有谣言状态图Fig.4 Rumor state diagram when R0=1.93

图4和图5对应的R0值分别为1.93、1.17，系统的局部稳定点分别是(0.221，0.379，0.174，0.261，0.249)，(0.344，0.031，0.094，0.264，0.208).

图5 R0=1.17时的有谣言状态图Fig.5 Rumor state diagram when R0=1.17

根据上述分析，可知基本再生数R0是决定谣言是否在网络中传播的重要参数.下面研究R0关于参数α3，β1和ε的变化趋势.通过计算可得:

(5)

根据公式(5)，在其它参数不变的情况下，R0随着α3(或ε)的增大而减小，R0随着β1的增大而增大.因此，想要控制R0的取值在1以下，可以增加参数α3或ε的值，或者减 小β1的值.

4.2 辟谣机制对传播过程的影响

为了检验辟谣信息可信度与辟谣个体影响力对谣言传播过程的影响，设定系统初始值U(0)=0.95，E(0)=0，T(0)=0.05，D(0)=0，R(0)=0.

实验3.基于上述设定，设置相关参数β1=β2=0.4，f1=0.6，f2=0.8，f3=0.5，ε=0.18，γ=0.1，b=0.1，k=0.9，δ=μ=0.015.令a取不同的值，仿真得到T节点的密度随时间的变化情况.具体如图6所示，并分析辟谣信息可信度的变化对T(t)的影响.

实验4.令a=0.1，b取不同的值，其他参数与实验3设定的参数保持一致，仿真得到T节点的密度随时间的变化情况，具体如图7所示，并分析参数辟谣者个体影响力的变化对T(t)的影响.

通过图6、图7可以看出，T节点密度变化呈现先增后减趋势.随着a、b取值的增大，在谣言传播前期，传谣节点密度的增长速度减慢，传谣者密度明显降低；在谣言传播中后期，T节点密度逐渐递减至趋于稳定，且趋于稳定的时间缩短.结果表明，在辟谣过程中，不仅要在谣言传播前中期利用高影响力用户发布辟谣信息，而且要提高辟谣信息的可信度，使更多公众积极辟谣，从而控制网络中谣言的传播.

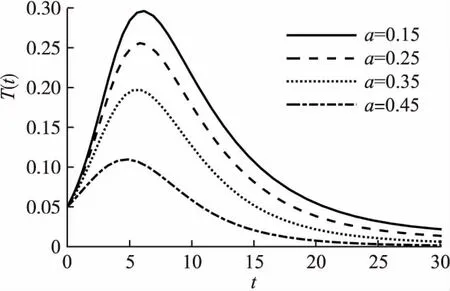
图6 辟谣信息可信度对T(t)的影响Fig.6 Impact of credibility of debunking information on T(t)

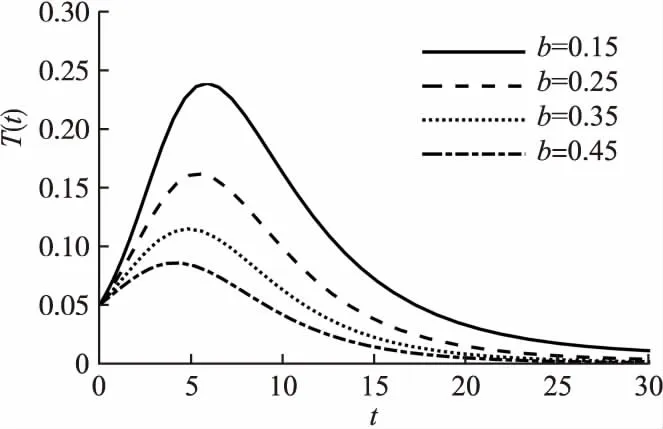
图7 个体影响力对T(t)的影响Fig.7 Impact of individual influence on T(t)

4.3 时延机制对传播过程的影响

本节将通过数值仿真实验来模拟社交网络谣言传播过程，探究时延机制对谣言传播的影响.

实验5.在仿真实验中，设定系统初始值U(0)=0.95，E(0)=0，T(0)=0.05，D(0)=0，R(0)=0.设定相关参数β1=0.5，β2=0.5，f1=0.6，f2=0.8，f3=0.5，ε=0.18，γ=0.1，λ=w=0，δ=0.001，μ=0.005，参数k分别为：1/2，1/4，1/8，1/16，对应的时间延迟分别为2h，4h，8h，16h.分析k取值的变化对潜伏者节点和传谣者节点密度的影响，如图8和图9所示.

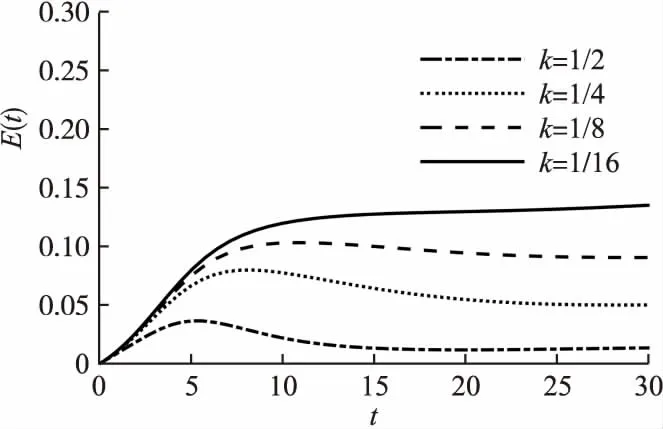
图8 时延机制对E(t)的影响Fig.8 Impact of time delay mechanism on E(t)

从图8和图9可以看出，随着k取值的减小，即潜伏时间的增多，潜伏者节点密度增加，传谣者节点密度减少，说明网络中离线节点的存在会延迟信息的传播，并且未知者节点中的离线节点的潜伏期越长，延迟效应越大.针对这个变化，相关部门可以在谣言扩散初期，尽早识别到谣言并通过后台对谣言进行一定程度的删除，进而延缓离线节点阅读到谣言的时间.

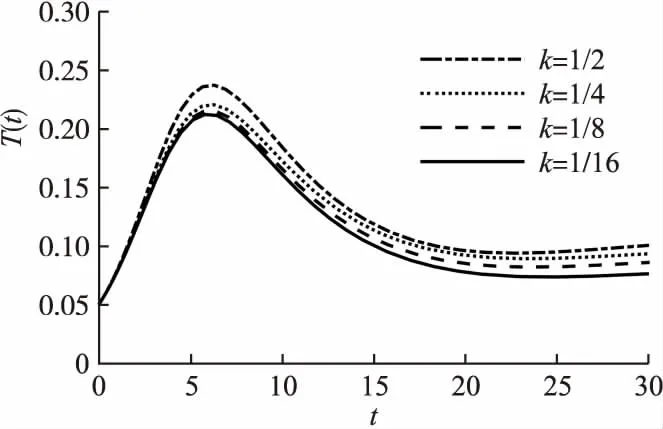
图9 时延机制对T(t)的影响Fig.9 Impact of time delay mechanism on T(t)

4.4 模型对比分析

将本文提出的UETDR模型与传统的SIR模型、SEIR模型进行对比实验.系统初始值的设定与实验1保持一致，设定UETDR模型相关参数δ=μ=0.01，α1=α2=0.25，α3=ε=0.15，k=β1=0.6，β2=γ=0.2，θ=0.3，SIR、SEIR模型参数取UETDR模型对应的参数值.仿真分析了传谣节点密度随时间的变化情况，如图10所示.

图10 UETDR模型、SIR模型和SEIR模型的对比Fig.10 Comparison of the UETDR model，the SIR model and the SEIR model

由图10可以看出，网络达到平衡状态时，SIR模型、SEIR模型、UETDR模型中的传谣节点的密度分别为0.938，0.665，0.379.在实际生活中，并不是所有的网络用户都是处于在线状态，因此时延机制将网络中的未知者划分为在线状态和离线状态，更好地区分了社交网络中的用户角色.对比SIR模型，在SEIR模型和UETDR模型中，由于潜伏节点的加入，传谣节点密度的增长速度降低.对比SEIR模型，UETDR模型传谣节点密度达到稳定状态所需要的时间更短，可以说明辟谣机制的加入，降低了其他节点用户转化为传谣节点的概率，使得传播节点密度峰值更低，网络中谣言存在的时间缩短，验证了模型的有效性.

5 结 论

在现实的社交网络中，由于谣言传播与用户的行为、外部社会影响紧密相关，针对未知者存在在线状态和离线状态的情况，辟谣信息可信度和辟谣者辟谣力度存在差异的特点，建立了基于时延机制和辟谣机制的社交网络谣言传播模型，并将辟谣机制以概率函数的形式融入到模型中，使得模型更加符合现实社交网络的谣言传播规律.计算了模型的平衡点和基本再生数，并通过理论分析和数值仿真实验验证了平衡点的存在性和局部稳定性.通过数值模拟，针对实际社交网络中离线状态用户浏览信息存在时间延迟的情况，仿真分析了时延机制对谣言传播过程的影响.针对政府或公众人物会对谣言积极辟谣的情况，仿真分析了辟谣机制对谣言传播过程的影响.结果表明，基于传统传染病动力学模型改进的UETDR模型能有效降低传谣者密度并缩短谣言存在的时间，使网络更快地趋于稳定.进一步，将本文提出的模型与传统的模型进行对比，验证了本文模型的有效性.

最后，通过对仿真实验的结果分析，从个人行为、危机管理以及技术等3个角度得出一些控制谣言传播的建议.从个人行为角度，针对未知者，可以通过宣传科学文化知识提高用户的知识水平，增强用户对谣言的辨别能力，从而降低未知者转化为传谣者的概率；针对造谣者，可以给予一定的警告和惩罚；针对辟谣者，应该鼓励高影响力的用户积极对谣言进行辟谣，并适当地加强辟谣的力度.从危机管理角度，相关机构应该密切关注网络活跃用户的行为，了解用户的需求，积极营造健康的网络环境，以便预防突发事件的发生.从技术角度，互联网平台可以建立一个谣言识别系统快速识别谣言，在谣言传播初期阶段，对谣言进行有效的屏蔽，降低用户阅读到谣言的概率，延缓谣言在传播初期的传播速率.

本模型主要考虑了线上因素对谣言传播的影响，而忽略了线下因素，线下的谣言传播也可能对网络谣言传播有影响，另一方面，数据驱动模拟是研究复杂系统动力学的一种流行方法.未来的研究可以考虑提出一个线上线下相结合，并由大数据驱动的模型来进行谣言动态的有效模拟.