指向数学运算核心素养的向量解题教学
2022-01-26吕增锋
吕增锋
(象山县第二中学,浙江 象山 315731)
学生认识数学就是从学习运算开始:幼儿时学习计数,小学学习加减乘除四则运算,初中学习平方、开方及比较抽象的符号运算,高中学习的运算更加多样:除了具体的数字运算外,还有逻辑运算、几何运算等.数学运算是“童子功”,按理说学生的运算能力不会差,但大量调查数据显示:当前高中学生的数学运算能力不容乐观.
实践证明:单纯的运算训练无法支撑起持续发展运算能力的重任,站在学科核心素养的高度对运算素养进行统一谋划才是治本之道.当然,“数学运算”一旦上升到素养层面,就不单单指数学计算能力,而是“数学运算核心素养”,它是在明晰运算对象的基础上,依据运算法则解决数学问题的素养,主要包括:理解运算对象、掌握运算法则、探究运算思路、选择运算方法、设计运算程序、求得运算结果等[1].数学运算核心素养是数学运算能力的根基,是数学思维发展的锚点,对促进思考模式的规范化、程序化,树立一丝不苟、严谨求实的科学精神具有重要作用.
1 向量是发展数学运算核心素养的绝佳载体
数学运算核心素养不会凭空产生,它需要以具体的教学内容为载体、通过运算实践来获得,而不同的数学知识模块,其运算素养的指向也不尽相同.比如,集合与逻辑用语强调的是集合运算与逻辑运算;圆锥曲线关注的是化简与变形能力,培养的是学生耐心细致的思维品质;排列组合培养的是计数技巧及算法思想.这就意味着知识模块所包含的运算越丰富,它对于数学运算核心素养培养所起的作用也就越大.在所有高中数学知识模块中,运算最为丰富的非向量莫属.
1.1 向量的运算对象多样
向量是沟通三角、代数、几何三大领域的桥梁,它既有数的属性,又有形的特征;既有代数运算,又有几何运算;既有二维平面的表征,又有三维空间的推广.因此,向量的运算对象就更具多样化:它可以是向量与向量之间的运算,如向量的加减法、数量积、向量积、混合积等;可以是实数与向量之间的运算,如数乘运算;可以是有向线段之间的运算,如平行四边形法则与三角形法则;可以是点与点之间的运算,如坐标运算;还有符号之间的运算,如把一个向量用其他向量来表示……向量这些运算几乎囊括了高中数学全部的运算对象,这对于学生在关联或综合情境中如何确定运算对象具有象征意义.
1.2 向量的运算法则独特

1.3 向量的运算方法灵活
通常在向量运算中,既可以由“形”感知,如借助向量运算的几何意义,通过直观感知获得运算结果;又可以从“数”入手,而数的运算又有“基底运算”和“坐标运算”.向量运算方法的灵活性造就了解题方法的多样化,入口宽、方法多是向量运算的常态.
2 指向数学运算核心素养的向量解题教学
数学解题教学中主要是运用数学运算来解决数学问题,突出体现了数学方法的范式.学生通过数学解题不仅训练了数学运算能力,而且加深了学生对数学对象和关系的理解,形成了有序地、合乎逻辑地认识与表达数学的理性精神[2].也就是说,数学运算是解题的基本手段,通过解题又能发展学生的运算素养,数学运算与解题是相生相长的关系.那么,如何使向量的解题教学指向核心素养呢?
2.1 读懂向量语言,理解运算对象
数学语言是表达科学思想的通用语言和数学思维的最佳载体,实现有效交流的前提就是学习和掌握数学语言,而且从某种程度上讲学习数学就是学习数学语言.数学语言一般分为文字语言(自然语言)、符号语言、图形语言.这3类语言各有千秋,文字语言表达直接,易于理解;符号语言书写简洁,表达严密;图形语言表现直观,启迪思维.不论用哪种语言表示,读懂语言,把它转化成易于学生理解的表达是解决问题的第一步.

1)|p-a|+|p-b|=2m(其中m>|a-b|),向量p所对应的点的轨迹是椭圆,双曲线也可以进行类似的定义.
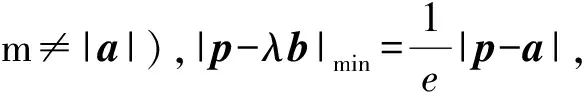
用向量语言表示虽然更具简洁性,但也加重了抽象性,导致学生无法直接读懂其所表达的内涵,需要借助数学运算来“翻译”.

分析此题涉及的向量多达4个,包含了数量积运算、模运算等多种运算,构成了复杂的向量关系式,这给学生的读题制造了不小的障碍,只有通过运算才能厘清其中的关系.


图1


通常可以这样解:设椭圆的另一个焦点为A1,则
得
2.2 一题多解,理解算理
依据数学的法则公式等进行数学运算,这是数学运算素养的初级阶段.而能够在理解运算的算理的基础上,根据问题中的相关条件,合理、正确和熟练地获得运算途径,灵活采用不同的运算方法与策略解决问题,这是数学运算素养的高级阶段.因此,多视角地分析问题,开展一题多解,是实现数学运算素养从初级阶段到高级阶段跨越的有效途径.

(2013年浙江省数学高考理科试题第17题)





从而



下面的过程和解法1一致(略).
解法4(几何视角之平行四边形法则)不妨设x≠0,由b=xe1+ye2,得
从而

图2
由于向量的多重属性与独特的运算性质,导致向量问题往往有多种解法.上述问题给出了4种解法,如果进一步挖掘还会有更多的解法.当然,指向运算核心素养的解题教学并不是为了获得更多的解法,而是在一题多解的过程中明确算理,而平面向量运算的算理就是从代数与几何两个视角,把条件与结论充分代数化,再借助方程与函数思想、直观感知等手段进行解决.
2.3 解题反思,形成算法
解题反思是一种元认知活动,它是通过对解题过程的再次思考,探究解题过程中所蕴涵的思想方法、规律模式、算法套路等.解题反思的过程不仅有益于巩固知识,熟练方法,分化和贯通整个思想和策略,而且能够促使算法结构更完善.解题的完成并不意味着解题活动的结束,对解题过程的回顾才是学习的重头戏,数学运算的算法化与程序化也是在这个过程中得以实现的.解题反思一般可以从所涉及的知识与思想方法、问题之间的联系、解题的程序、运算推理的过程、数学活动的结果等方面进行,从而获得某类运算或某类题目的一般算法.比如,对向量的“代数化”可以这样反思,如图3.

图3
虽然说,数学运算是数学解题活动中最为普遍的方式之一,但如果在解题中只是“就题论题”,或者一味地追求解题的结果,而不去提炼解题中的运算法则、算理与算法,那么数学运算素养就不能得到持续发展,因此,指向核心素养才是数学解题教学的真谛所在.
