基于APOS理论的“函数的概念”教学设计
2022-01-26曹毅
曹 毅
(浙江师范大学附属中学,浙江 金华 321000)
概念教学有两种基本形式:概念同化与概念形成.根据教材设置,本节课应采用“概念形成”的方式进行教学,笔者认为APOS理论能满足这些要求,使数学核心素养渗透整个教学过程.APOS理论通过建立心智结构使学习者形成数学概念,心智结构的构建分为4步:活动→过程→对象→图式,即抽象特征—归纳共性—形成概念—同化整合.
1 课前准备,研读教材
1.1 教材内容解析
《浙江省普通高中学科教学指导意见数学(2021年版)》中明确指出:函数是描述客观世界变量关系和规律的最基本的数学语言和工具,是贯穿高中数学课程的主线.学生在初中阶段学习的函数概念是“变量说”,即函数是刻画变量之间的对应关系.在高中阶段,学生要在“集合论”的基础之上建立“对应关系说”,其核心是实数集合的特殊对应关系.因此本节课的教学重点是从现实问题出发,让学生抽象、建立以集合语言为基础的函数概念.
1.2 教学目标解析
笔者基于APOS理论,让学生通过现实问题,在得到对应关系的基础上,体会变量范围对描述问题的重要性,比较函数不同的表达形式,抽象出函数的共性,构建“集合—对应关系说”观点下的函数概念;再引导学生用高中函数概念刻画一次函数、二次函数与反比例函数,以同化新知;最后,让学生通过构建问题情景,使其中的变量关系满足给定的函数表达式,以进一步体会作为数学工具的函数是如何描述客观世界的.
2 构建心智结构,渗透核心素养
2.1 抽象特征,归纳共性,形成概念(APO)
投屏初中函数概念:一般地,在某变化过程中,设有两个变量x与y,如果对于x的每一个确定的值,y都有唯一确定的值与它对应,那么y是x的函数,x是自变量.

学生意见不一,根据初中学习的函数概念并不能进行判断.
师(板书课题):要解决这些问题,需要进一步学习函数概念.
根据APOS理论,我们将高中函数概念的形成分成以下几步:
1)通过问题1关注变量的取值范围;
2)通过问题1和问题2的比较,进一步认识定义域、值域;
3)通过问题3中图像的对应关系,得到图像的表达式;
4)通过问题4中表格的对应关系,得到表格的表达式;
5)归纳4个函数的共性,概括函数的本质特征;
6)得出函数概念.
问题1高铁是我国制造业的骄傲,是中华民族伟大复兴的标志之一.列车行进的路程S(单位:km)与运行时间t(单位:h)的关系可以表示为
S=350t.
(1)
师:根据初中学习的函数概念,请同学们判断S是否为t的函数?为什么?
生1:是.因为在行驶过程中,对于时间t的每一个确定值,路程S都有唯一确定的值与它对应.
师:“根据对应关系S=350t,这趟列车加速到350 km/h后,运行1 h就能前进350 km”,这样的说法正确吗?如何更精确地表述S与t的对应关系?
生2:对于集合{t|t≤0.5}中每个时间t的确定值,通过式(1),路程S都有唯一确定的值与它对应.
设计意图让学生在解决问题时发生认知冲突,发现初中所学概念的局限性,并注意到变量范围,开始描述变量范围中的一一对应关系.
问题2保护劳动者合法权益是全社会的共识.为了符合2021年5月21日最新推出的《中华人民共和国劳动法》,某公司确认工资标准为每人每天350元,每周付一次工资,工人每周至少工作1天,至多6天,那么工资w与一周工作天数d的关系是
w=350d.
(2)
师:仿照问题1,用精确的语言描述本问题中w与d的对应关系.
突发情况:学生回答天数d的集合为{d|1≤d≤6},笔者立即让学生对比集合{d|1≤d≤6}与{1,2,3,4,5,6},让学生认识到在描述问题时应与实际相符合.
生3:对于集合{1,2,3,4,5,6}中每个天数d的确定值,通过式(2),工资w都有唯一确定的值与它对应.
师:问题1与问题2中的函数有相同的对应关系,你认为它们是同一个函数吗?为什么?
设计意图使学生进一步关注到定义域与值域,体会它们对于函数概念的必要性.
问题3随着政府持续治理,我国的环境有了根本性的改善.请根据书本上的图1(略)回答:如何根据该图确定这一天任何一个时刻t的空气质量指数值I(以下简称AQI)?
设计意图让学生指出图像中包含的对应关系,为判断是否为函数提供依据.
师:你认为这里的I是t的函数吗?如果是,请仿照前面的方法描述它们的对应关系.
生:对于时刻t的集合A={t|0≤t≤24}中任意一个值t,都有唯一确定的AQI值与它对应,所以I是t的函数.
师(引导):从图像出发,我们并不能准确描述I的取值范围,需要用AQI值所构成的集合B3,而这不会影响对问题的描述,且I的取值范围C3满足:C3⊆B3={I|0 设计意图让学生认识到图像也是一种函数表达形式,值域是函数值所在集合B的子集. 问题4恩格尔系数是反映人民生活水平的指数之一,请根据书本上的表1(略)回答:你能得出该省城居民生活质量发生了怎样的变化?你认为恩格尔系数r是y的函数吗?仿照前面的问题精确描述它们的对应关系.根据恩格尔系数的定义,r的取值范围为B4={r|0 设计意图让学生认识到表格也是一种函数表达形式,此处教师根据恩格尔系数的定义对函数值所在的集合B4的合理性进行了解释. 归纳共性根据上述4个问题中的函数,归纳函数的共性,并概括出函数的本质特征. 教师给出表1,让学生归纳4个问题的共性. 表1 4个问题中的函数特征 师:4个函数有哪些共同特征? 教师引导学生得到:①都有两个非空数集,分别用A与B表示;②都有一个对应关系. 师:自变量与因变量是如何通过对应关系联系起来的? 教师引导学生得到:虽然表达方式不一样,但这4个函数都满足“对于数集A中的每一个x,按照某种对应关系,在数集B中都有唯一确定的y值和它对应”. 师生活动引导学生最终形成函数的概念. 1)下列给出的对应关系中,是函数的是 ( ) 2)设集合A={x|0≤x≤2},B={x|0≤x≤2},下列对应关系f不能表示从集合A到集合B的函数是 ( ) A.f∶x→y=xB.f∶x→y=2x A. B. C. D. E. 设计意图2个练习分别从不同角度巩固函数概念,让学生更好地理解函数概念中的任意性与唯一确定性以及值域是集合B的子集. “图式阶段”是指让新的概念形成知识图式,并把这个图式纳入已有认知结构中的教学过程,即知识的同化.笔者安排了两个教学活动帮助学生完成这一过程. 活动1用高中所学的函数概念重新描述一次函数、二次函数与反比例函数. 教师引导学生得到一次函数的描述:f把R中的任意一个x,对应到R中唯一确定的ax+b(其中a≠0).学生独立思考并描述二次函数与反比例函数. 活动2试着构建问题情境,使其中的变量关系可以用解析式y=x(10-x)来描述. 笔者在活动2中安排了分组讨论,学生在充分理解概念的基础上,构建了例如销售总额情景、物体匀加速运动情景等很多精彩的答案. 高中函数概念是在初中函数概念基础上的再抽象,因此本节课的引入必须强调“对应关系说”的必要性,让学生认识到“变量说”的局限性.学生也需要通过对第三章章前语的解读,并与第一章“集合”的内容产生呼应,认识到在集合基础上建立函数概念的必要性. 对“必要性”的研究能帮助学生更好地理解函数概念,再让学生完整地经历“问题—观察—比较—分类—分析—归纳—抽象—概括”的过程,得出函数概念也就水到渠成了. 新生概念的学习是学生主动构建知识的过程.在备课阶段,教师需要研究学生建构过程中可能产生疑惑的环节,了解学生的最近发展区,找到学生已有的认知结构与新学概念之间的结合点,从而确定教学内容与顺序,精心设计教学活动. 若放弃对书本上4个问题的讲解,直接给出函数概念,高一新生则很难体会函数概念的形成,只能机械记忆.那么学生如果缺乏对数学概念的理解,就不可能完成对新知识的同化,达到构建心智结构的目的.学习数学的目的是认识、理解客观世界,学生不能简单地将学数学与做题目等同,此版本教材较好地将该目标渗透到每一章节中.教师在上课前一定要研读教材,体会教材设计的初衷,落实数学核心素养,使学生能自然地使用数学语言描述客观世界.
2.2 训练巩固,理解概念

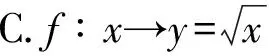
2.3 同化整合
3 教学反思
3.1 强化必要性是学习函数概念的前提
3.2 APOS理论下函数教学的建议
