流化床液固两相传质过程的模拟研究进展
2022-01-26任盼锋海润泽李奇李文彬余国琮
任盼锋,海润泽,李奇,李文彬,余国琮,3
(1 天津大学化工学院,天津 300072; 2 中圣(天津)新能源科技有限公司,天津 300453;3 化学工程联合国家重点实验室(天津大学),天津 300072)
引 言
液固两相流化床是一类典型的基于颗粒-流体系统的工业反应器,凭借其液固相接触高效、传质和传热性能好、颗粒分布均匀等优点[1-2],被广泛应用于生物化工[3-5]、废水处理[6-8]、冶金[9]、石油[10]等许多工业过程中[11]。然而,由于液固两相流化床体系内颗粒-流体的流动不均匀性、流域的多态性及常伴随的湍流效应等,导致液固两相流动及其耦合的传质过程十分复杂。目前对于这一体系的了解仍然十分有限,而此类型反应器的设计、放大和优化也仍然是基于经验性的途径[12],这大大限制了其工业应用。
近些年,流体力学与数值计算的交叉研究促进了计算流体力学(computational fluid dynamics,CFD)这一新研究领域的形成。这一多学科的发展后来扩展到传热,与传热理论相结合,产生了计算传热学(computational heat transfer,CHT)。这两个新的研究领域的建立帮助科学家和工程师解决了许多难题,目前已经在涉及流体流动、传热工程问题的预测,以及工业设备的放大和操作参数的优化过程当中被成功应用。然而,化工工程师所处理的不仅包括流体流动和传热,而且还包括质量传递和化学反应。传质特别是浓度分布的详细信息是化工设备设计和评价的基础,是评价工艺效果或效率的基础,其传质速率从根本上会影响一个反应装置或者一个反应系统的效率及其相关的经济指标[13]。但传质过程及其传质特性往往十分复杂,通常涉及湍流、多相态、化学反应、传质扩散、不稳定运行以及设备内部构造等诸多因素的影响。为了简化问题,传统的浓度场预测常采用经验方法,不仅不可靠,而且缺乏理论基础。直到2003年,天津大学余国琮教授团队通过类比CHT 模型,提出了用以封闭湍流传质微分方程以精确求取浓度分布的模型,并成功应用于精馏过程的数值模拟研究中[14-15],进而使传质过程模拟研究从以往的基于实验/经验的方法转变为基于理论的严格方法,拉开了计算传质学(computational mass transfer, CMT)研究的序幕,为流化床液固两相传质过程的研究带来了新的研究方法。CMT的模拟结果可以提供更多可视化和详细的动量、热量和质量传递的信息,有望成为液固两相流化床反应器设计、放大和优化的有效方式。
对于流化床液固两相传质过程而言,数值模拟可以更深入地了解设备内部的流动行为和传质规律,是对有限实验测量的重要补充,而采用适合的模型精准预测传质过程对反应器的应用具有重要意义。本文综述了近年来关于流化床液固两相流动与传质过程特征以及传质过程模拟方法方面的研究进展,以期为液固两相流化床反应器的结构设计、装置放大、优化操作以及性能预测等方面的模拟研究提供参考。
1 流化床液固两相传质过程特征
流化床是凭借流态化技术强化颗粒与流体之间接触和传递效率的重要装置,其主要优越性体现在:(1)处于流态化的固体颗粒尺寸较小,比表面积较大,大大提高了两相间的接触程度;(2)流态化颗粒处于强烈的湍动状态,两相接触界面不断更新,两相间速度差较大,强化了两相间的热、质传递;(3)反应表面积的增大和传递过程的强化,使其所进行的物理化学过程更为完全,更为充分,大大提高了生产装置的工作效率;(4)流态化技术有助于加工过程中物料的运输和转移,进行连续化操作,实现过程自动化和生产规模大型化。
1.1 液固两相流化床的类型
液固两相流化床是指利用液体将颗粒进行流化,进行液固相反应过程的流化床反应器。根据有无颗粒循环的特征,可分为无颗粒循环的液固流化床(liquid-solids fluidized bed,LSFB)和有颗粒循环的液固循环流化床(liquid-solids circulating fluidized bed,LSCFB)。
LSFB 是固体颗粒在液体的作用下流化的常见设备,其结构如图1(a)所示。通常,LSFB 主要由立管、液体分布器和一些检测控制部件组成。立管底部装有液体分布器,立管主体含有许多颗粒。当自下而上的液体通过颗粒床层时,液体对颗粒产生曳力,随着表观液速的增加,曳力增大,使得颗粒开始慢慢波动,颗粒床层也开始变得松动并略有膨胀,但颗粒仍处于非自由运动的状态,此时称为临界流化状态。随着表观液速的继续增大,颗粒开始全部悬浮在向上流动的液体中,此时的速度被称为最小流化速度[16-18]。再继续增大液速,加大的曳力使得颗粒在液体中开始自由运动,床层膨胀程度加大,床层空隙率变大,此时颗粒与液体之间的曳力恰好与其净重力相等,床层达到了一定的膨胀高度且出现了明晰、稳定的液固界面。随着颗粒的上下运动,液固体系的返混也变重[19]。
当液体速度增加到颗粒的终端速度以上,颗粒就会被带出立管,形成LSCFB。LSCFB 的出现丰富了液固两相流化床的发展,近些年被广泛应用在食品、生物化工、污水处理等方面。所用的颗粒密度和终端速度较小,形成了完整的颗粒循环,并实现了可连续性的操作,大大提高了反应器的生产效率[20]。图1(b)为LSCFB 的结构示意图,主要包括提升管、降液管、液固分离器、顶部固体回流管、底部固体回流管、提升管分布器等结构。值得注意的是,为了更好地控制颗粒的循环,LSCFB 提升管中的液体入口常常分为主流和辅助流,主流主要控制提升管中液速的大小,而辅助流则用以控制颗粒的循环速率。
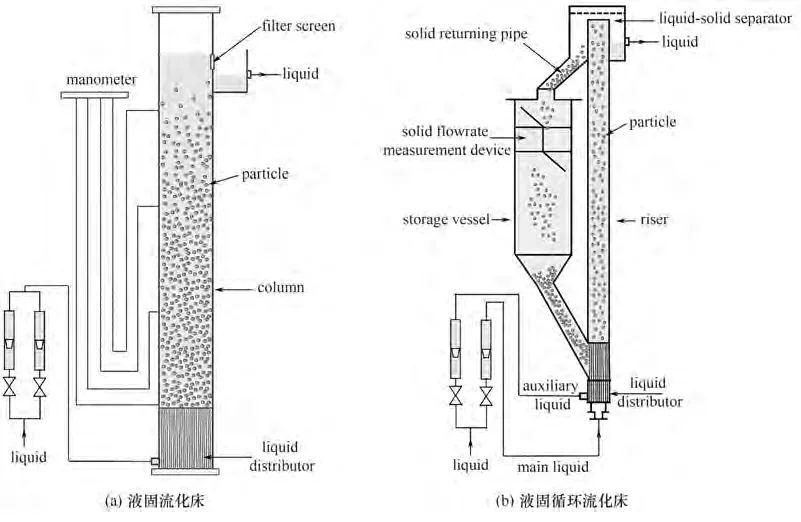
图1 液固两相流化床装置示意图Fig.1 Schematic diagram of liquid-solids two-phase fluidized bed devices
1.2 流化床液固两相流动特征
对于液固两相流态化,颗粒能均匀分散在液体中,具有较均匀的床层结构。而传质过程与两相流动特性密切相关,在不同条件下流化床内颗粒性质、流体的性质与速度以及流化床的结构等都会对其流动行为和传质过程造成一定的影响。另外,在液固两相流化床中,常常由于各种机械驱动和介质驱动会不可避免地引入少量的气泡,这些对流化床液固两相流动造成了微弱的影响,目前对气液固三相流化床传质和流动的数值模拟研究还处于发展阶段[21-23]。
1.2.1 特征参数 当流体通过颗粒床层时,流体对颗粒产生曳力,随着流速的增大,曳力也随之增大,当曳力等于颗粒床层的净重力时,或当流体通过床层时的压降刚好等于单位床截面上颗粒重量时,颗粒开始流化,此时流体的表观速度称为起始流化速度umf,又称最小流化速度或临界流化速度。当超过颗粒的起始流化速度时,床层开始膨胀,液速加大,床层膨胀程度变得更大。目前,液固流化体系的起始流化速度的求解方法主要是从流化床和固定床的压降关系考虑,结合实验数据针对不同的Reynolds数范围经关联得到最小流化速度的半经验公式或一些纯经验公式去进行求解[24]。

固体颗粒随着液速的增大而与流体作等速运动时,颗粒的净重力等于液体流过颗粒表面产生的曳力,此时的颗粒速度称为颗粒终端速度Ut。如果液体是向上运动的,且其向上的液速大于颗粒的终端速度,则颗粒就会被液体带走而形成有颗粒循环的流化床。常常采用结合曳力系数Cds与颗粒终端Reynolds数Ret进行求解[25]:

1.2.2 颗粒运动及分布 针对传统的LSFB,早在20世纪50年代就已进行了大量的研究[11,26]。研究结果表明,LSFB 处在均匀的理想流态化状态下,颗粒均匀地悬浮在向上流动的液体中,呈现出各向均匀的散式流态化现象。在1954 年,Richardson 和Zaki[26]提出了操作液速和床层空隙率间的R-Z 方程。在给定液体表观速度后,利用此方程即可求出床层空隙率,如果知道LSFB 中颗粒总的质量,即可求出床层的膨胀高度,这解决了LSFB 设计中的关键问题,对促进流化床的发展具有重要意义。其经验公式如下:

在LSCFB 中,颗粒形成有规律的循环,早期研究已发现了流体流速的不均匀性分布,以及由此导致的局部颗粒固含率的径向不均匀性分布(环-核结构)现象[27],这表明液固两相流化床中颗粒分布呈现一定的规律和复杂性。Lan 等[28]应用LSCFB 提取了牛的血清蛋白,降液管用于蛋白质的吸附,液体的速度小于颗粒的终端速度,颗粒向下运动,停留时间较长;提升管用于蛋白质的脱附,液体的速度大于颗粒的终端速度,颗粒向上运动,停留时间较短。颗粒形成完整的循环,大大提高了蛋白质的提取效率。Zhu 等[29-30]通过实验测量发现,LSCFB 中相含率和液速在径向上呈现不均匀分布,在轴向上呈现均匀分布,结合实验数据建立了LSCFB 中相含率分布的环-核模型[27],如图2 所示。环-核模型描述了颗粒含率的非均匀径向分布,认为中心区域颗粒浓度高于边壁颗粒浓度,其模型的预测值与实验结果吻合较好。

图2 液固循环流化床的环-核流动结构模型示意图[27]Fig.2 Schematic diagram of core-annular flow structure model for LSCFB[27]
1.3 流化床液固两相传质过程
化工装置中的浓度分布反映了装置传质性能最直接的特性,如果能够了解液固流化床内浓度分布,对深入理解该装置的传质过程机制、设备及流动状况对效率的影响规律具有十分重要的意义。目前的CFD 模拟技术为这一问题的解决提供了有效保障。而流化床中溶质在颗粒表面的传质过程一般需要经过如下步骤[31]:
(1)相间传质,溶质依靠对流从流体主体通过薄膜或边界层到颗粒的外表面;
(2)相内传质,溶质依靠孔道扩散从颗粒的外表面到达颗粒的内表面;
(3)溶质沿孔道表面扩散和吸附。
在CFD 中,采用双流体模拟方法的q相(q=l为液相,q=s为固相)组分守恒方程可表达如下:

2 流化床液固两相传质过程模拟方法及数值模型
对于流化床液固两相的传质过程模拟而言,目前还不及对流动特性和传热过程的研究,尚处于发展阶段。图3 总结了CFD、CHT 和CMT 三者在传递过程的数值模拟之间的联系,三者相互渗透但又有不同侧重点,CMT 的研究是建立于CFD 基础之上,结合传质理论的重要模拟方法。自2003 年余国琮带领团队发展CMT 以来,已经形成了一定的理论体系。刘国标[32]采用CMT 的方法成功模拟了填料床中传质与反应的过程;紧接着该团队将CMT 应用到了化学反应和化学吸收等过程[15,33-37]。近年来,李文彬等又将该方法的应用拓展至颗粒流化系统的传质过程模拟,成功模拟了气固两相鼓泡流化床[38-40]、填料床[41-47]、气固循环流化床上行床[48]、气固循环流化床下行床[49-50]以及液固两相膨胀流化床[51]、液固两相循环流化床[52-53]等。

图3 传递过程的数值模拟Fig.3 Numerical simulation of transfer process
2.1 两相流模拟方法
目前对颗粒-流体两相流的数值模拟研究较多,但总地来说可以分为三种方法:直接数值模拟方法(direct numerical simulation,DNS)、欧拉-拉格朗日(Eulerian-Lagrangian, E-L)方法和欧拉-欧拉(Eulerian-Eulerian,E-E)方法。图4展示了液固两相流不同模拟方法。

图4 液固两相流不同模拟方法Fig.4 Different simulation methods of liquid-solids two-phase flow
DNS 方法中,对离散颗粒在拉格朗日坐标系中受力情况和运动轨迹进行跟踪研究,颗粒之间的相互作用可以根据相关的数学模型直接确定,这样就避免了颗粒相的本构方程和颗粒拟流体化的计算困难。但这个方法随着颗粒数目的增加,计算量呈现指数型增长,对计算的内存要求很高,目前在液固两相流化床的模拟中应用较少,在计算传质研究中实用性差。
E-L方法中,将液体当作连续的介质,而视颗粒为离散体系,在欧拉坐标和拉格朗日坐标系下分别考察流体的流动和颗粒的运动,通过牛顿运动定律对其进行求解。这种方法通过考察单个流体质点的运动行为来分析整个流场,是研究个体质点的流体力学,描述了流体质点的位置、速度和加速度,以及各质点之间的相互作用。在计算传质的模拟中,常对颗粒的运动轨迹并不十分关注,而更关注固定空间点上的物理量。另外,这种方法中流场的质点数量巨大,在CFD 中的计算量更大,很难在工业规模的传质计算过程中得到应用[54]。
E-E方法中,把颗粒当成拟流体,认为液体与固体颗粒是相互渗透的连续介质,两相都是在欧拉坐标系下处理。这种方法没有追踪个别的质点而是关注空间点,即在固定的空间点上来考察流体的流动,将流体的所有的空间点的流动规律综合起来可以获得整个流场的流动规律,这类模型经历了无滑移模型、小滑移双流体模型、有滑移-扩散的双流体模型以及近年来发展起来的以颗粒碰撞理论为基础的双流体模型(two-fluid model, TFM)[55]。TFM 能通过颗粒黏度和压力来考虑颗粒-流体间的相互作用,尤其是可以预测不同颗粒浓度下颗粒相的详细的空间分布信息,十分便于工业传质过程的计算模拟,容易和实验测量的结果进行比较,目前已成为两相流CFD模拟方法的主流。
2.2 湍流传质扩散模型
流化床的设计和放大一直是工业应用中的难题,其主要有两个原因:一是流化床中的流动行为非常复杂,且常被认为处于非线性的湍流状态,这为理论分析和数值计算带来了很多数学和计算的困难;二是湍流传质过程复杂,其影响因素诸多,且目前对传质-流动耦合理论的认识还远远不够[56]。目前主要研究的湍流传质扩散模型有特征数模型、双方程模型和雷诺质流模型。
2.2.1 特征数模型 早期人们意识到,对湍流传质扩散的充分了解必须建立在湍动的定量描述基础上,这涉及漩涡的尺寸和运动,因为计算机的发展有限,根据经验,人们常常将湍流传质扩散系数与湍流黏度进行关联,并假设了一个恒定的Sct,工程师常凭经验从0.6~1.0 范围选取[57],很难确定,且不能保证其可靠性。其湍流传质扩散系数可由式(7)进行计算:

另一种特征数的方法是利用表示湍流传质扩散程度的湍流Peclet 数(Pet)求解,而Pet一般是通过分析惰性示踪剂实验数据与流动Reynolds 数Re、物性以及设备的特征尺寸等相关联。传质Pet的定义为:

式中,L为设备的特征长度。Pet可以表示为由经验确定的常数,但文献中也常表示为一个特征数方程式。这种方法虽然比Sct可能好一些,但也有如之前所说的一些缺点。例如van der Meer 等[58]根据此特征数方法的描述,提出了将湍流传质扩散系数与动量场结合起来,经过和实验对比得出了经验关联式:

但这些特征数方法缺陷很大,可以想象,采用不同的实验关联式或者特征数将得到不同的浓度场,这就给模拟带来了很大的不确定性。并且许多研究者[31,59]也已经指出Sct并非是一个常数,也不仅仅与速度场有关,在轴向和径向上都有一定的分布,这就需要采用更严格的方法进行模拟。
2.2.2 双方程模型 2003 年,余国琮教授团队的刘伯潭[14]经过类比传热双方程模型,引用Boussinesq各向同性假设,将雷诺质流--- ——ui'c'表达为时均浓度梯度的函数,采用浓度方差与浓度方差耗散率的-c2-εc双方程模型对其进行了封闭求解,利用精馏塔的单块塔板浓度场模拟对模型进行了验证,模拟结果和实验数据吻合较好,从而证明了双方程模型的有效性。2005年,孙志民[15]扩大了塔板范围,应用到八块塔板上检测了该模型的有效性,指出Sct并不是常数。随后,双方程模型在化学吸收、吸附、固定床催化反应与气固流态化等中都得到了很好应用[60]。近来,Li 等[51-53]基于Boussinesq 各向同性假设在流化床中成功建立了液固两相的双方程湍流传质模型。

2.2.3 雷诺质流模型 以上特征数模型和双方程模型都引入了基于各向同性湍流扩散的Boussinesq假设,但大量实验观测表明湍流传质扩散的影响是各向异性的。为考察湍流传质扩散的方向性特征及其对传质过程的影响,近年来Li 等[48]又建立了雷诺质流方程封闭模型。这一模型不基于Boussinesq假设,从而能准确描述湍流传质扩散的各向异性特征。

李文彬等先后将雷诺质流模型应用在了气固鼓泡床[40]、填料床[42-44,46-47]、气固流化床[48]模拟中,对比了雷诺质流模型和两方程模型、Sct模型之间的差别,求解了各向异性的湍流传质扩散系数的分布情况,证明了雷诺质流模型的精确性。此模型优点如图5 所示,能更真实地反映湍流传质扩散系数的轴径向分布情况,但雷诺质流微分方程形式较为复杂,计算量较大,对长时间的传质过程模拟应用相对较难。

图5 气固鼓泡塔中各向异性湍流传质模型[40]Fig.5 Anisotropic turbulent mass transfer model in gas-solid bubble column[40]
2.3 液固相间传质系数
对于流化床中液固两相的传质过程,常将其视作物质从液相中扩散至固相表面而被固体吸收的过程,故一般可采用吸附传质方法[61-63]测定其传质系数。流化床中颗粒相浓度测定的困难,以及处理实验数据的模型假设认定的不同,导致实验结果差异很大,难以获得统一的关联式。表1 总结了流化床液固两相传质系数关联式和主要参数。

表1 流化床液固两相传质系数关联式和主要参数Table 1 Correlations and main parameters of liquid-solids mass transfer coefficients in fluidized beds
目前在考察液固两相流化系统的传质速率时,可以按照相近的实验或操作条件,选择上述关联式进行估算。在较低的Reynolds 数范围下,Fan 等[64]、Tournie 等[66]、Evans 等[68]以及Rahmant 等[75]的关联式实用性较好,而其余关联式的范围相对较广,在较高Reynolds 数时可能使用效果较好,但仍需要参考实验中的传质系数的实际大小,结合Schmidt 数范围选取以得到更加合理的计算结果。
3 流化床液固两相传质过程模拟研究进展
流化床液固两相传质过程的模拟是流动与传质的耦合问题,复杂的湍流流动行为及伴随的复杂湍流传质扩散,使得对这一问题的理论研究十分困难。近年来,结合先进的CFD 模拟手段,对流化床液固两相传质过程的模拟研究得到很大发展。
3.1 流动行为模拟结果
近年来,CFD 在液固两相流流场分析中的应用越来越受到关注。一般认为,液固两相流与气固两相流相比,两相密度差较小,颗粒的分布比气固两相更为均匀,湍流的影响也相对较小。另外,在颗粒表面存在薄薄的液膜,使得颗粒之间的碰撞概率和聚团程度都大大减小,甚至消失。目前,许多学者应用不同的数值方法对液固两相流的流动行为进行了研究,归纳总结见表2。

表2 流化床液固两相流动行为模拟Table 2 Simulation of liquid-solids two-phase flow in fluidized beds
通过对上述文献进行对比分析发现,液固两相流化床流动行为的模拟已经较为完善,模拟对象主要是LSFB和LSCFB的不同结构的实验装置,模拟方法主要有E-E和E-L两种。Ghatage等[91]采用双流体方法E-E 和颗粒离散单元方法E-L 进行了模拟对比,模拟结果都和实验吻合较好,但在模拟中颗粒离散单元方法(computational fluid dynamics and discrete element method, CFD-DEM)耗时较长;Wang 等[88]采用CFD-DEM 的方法,在研究中考虑了润滑力对模拟结果的影响程度,指出润滑力降低了LSFB 中的颗粒拟温度,对模拟结果的影响较小。一些研究者采用E-E的方法研究了不同物理结构对液固流化床流动行为的影响。Cornelissen 等[83]对分布器板的均匀分布和非均匀分布入口进行了模拟和比较,指出分布器板的几何结构对LSFB 内流动行为的模拟结果影响不大;Visuri等[87]对比了不同曳力模型在二维(two dimensions, 2D)和三维(three dimensions, 3D)模拟中的变化情况。结果表明,不同的曳力模型对模拟结果有着很大的影响,而2D和3D的模型预测结果变化较小。
许多研究者采用E-E 的方法研究了不同相间作用力模型和操作条件对模拟结果的影响。Reddy等[84]模拟了LSFB 从Reynolds 数为0.138 的层流状态到Reynolds 数为1718 的湍流状态下床层膨胀的动态变化情况,以及不同颗粒密度和直径下的二元颗粒混合物的流动行为,模拟中也出现了和实验相一致的颗粒层反转现象,并成功预测了两种颗粒完全混合的临界液速。Huang[86]重点研究了曳力模型和附加质量力对液固流化床内流动行为的影响。结果表明,曳力模型的选取对流动行为的模拟结果有着很大的影响,较重的颗粒体系下虚拟质量力对模拟的结果会产生一定的影响。Zhang等[89]在数值模拟中考虑了颗粒分散程度对动量方程的影响,预测了不同液速下LSFB流动行为的动态变化过程。Zhu等[97]建立了一个轴对称模型对LSCFB 提升管内的流动行为进行了模拟分析。其预测结果与实验数据吻合较好。利用脉冲技术预测了提升管内固体颗粒的停留时间,并且应用提出的CFD 模型预测了液体流速和固体循环速率对循环流化床性能的影响。随后,对降液管内的流动行为进行了模拟研究[93]。结果表明,颗粒床层的膨胀程度直接受降液管内表观液速和固体循环速率的影响,颗粒的停留时间更接近于平推流反应器,表观液速的增加降低了LSCFB 降液管内的固体颗粒的分散程度。
近来,Li 等[51-53]对不同曳力模型的适用性和相关模型参数的敏感性进行了考察。结果表明,对于较重的颗粒,Gibilaro曳力模型可以更好地预测其流动行为;对于较轻的颗粒,Gidaspow 曳力模型在流场方面具有更好的模拟结果,并且随着表观液速的增大,Gidaspow和Gibilaro曳力模型预测的膨胀率和实验的误差并不会随之增大。另外,颗粒-颗粒碰撞恢复系数和壁面反射系数都对流化床里的流动行为的模拟有一定的影响,尤其是在床层底部进口附近的区域对流动行为产生一定的影响,壁面反射系数对边壁附近固含率的分布和相速度的分布产生一定的影响。颗粒-颗粒碰撞恢复系数接近于1和颗粒壁面反射系数接近于0,将使LSFB 系统中的固含率分布更加均匀。
颗粒和流体的相互作用力对液固两相流化床流动行为的模拟预测起着关键性作用,曳力是最重要的相间作用力。在已发表的液固两相流化床的模拟当中,曳力模型主要有两大类:一类是基于平均化思想的曳力模型,即在单颗粒曳力模型的基础上结合实验数据,与固相体积分数以及颗粒Reynolds 数等进行经验关联,采用平均化方法对曳力模型进行修正得到多颗粒体系的曳力模型,常见的有Wen-Yu、Gibilaro、Gidaspow、Syamlal O’Brien、Ergun、Schiller-Naumann、Huilin-Gidaspow 和Haider-Levenspiel 等曳力模型;另一类是考虑了液固非均匀结构的曳力模型,常见的以能量最小多尺度原理(energyminimization multiscale,EMMS)[98]和Filter 曳力模型[99]为代表。Liu 等[90]就采用EMMS 的方法对LSFB 中的流动行为进行了模拟预测,模拟结果更加准确。
3.2 传质过程的模拟结果
组分浓度分布是评价液固流化床的传质效率的直接依据。然而,如前所述,由于液固两相流动的复杂性以及往往伴随湍流这一复杂因素,流化床液固两相传质过程及其组分浓度的准确预测十分困难。目前对液固两相流化床内湍流传质过程的研究报道还很少,其中要么忽略流体湍动对传质过程的影响,要么采取经验方法估计该影响的大小,其本质上都是一种近似。但已有文献报道,对于液固两相流化床,其中的湍流扩散对传质过程的影响往往占据主导,这提示人们采用近似的方法可能引起较大误差。如Mazumder等[100]的结果表明,在液固流化床的吸附过程中,表面吸附反应足够快,认为流化床中液固两相的传质过程受主要扩散过程控制,作者通过假定Sct常数估算湍流传质扩散,通过R-Z方程求解固含率分布,采用简单的一维轴向扩散模型对其进行模拟,其数值模拟结果和实验存在较大的误差。Kalaga等[101]基于示踪滞留分布实验提出了液相轴向扩散系数的经验关联式,其对湍流传质扩散系数可以进行较为准确的估算;另外,作者指出液体表观速度、颗粒大小、颗粒密度对传质扩散系数有很强的影响。Dadashi 等[102]建立了CFD模型来模拟LSCFB提升管中的蛋白质脱附过程,该模型更准确地研究了系统的性质,包括流体动力学、传质和动力学,但仍然采用Sct模型估算湍流传质扩散。模拟结果与实验结果比较存在较大误差。Derksen[103]采用格子玻尔兹曼的方法对液固流化床和固定床在静态和动态组合流动时的液固传质过程进行研究,指出了Schmidt数在颗粒周围到设备边界的大小并不一致。




图6 示踪剂扩散过程模拟结果[53]Fig.6 Simulation results of tracer diffusion process[53]
随后,Li 等将模型应用进行了扩展,对无颗粒循环的LSFB 蛋白质吸附过程[51]和有颗粒循环的LSCFB 提升管中蛋白质脱附过程[52]进行了模拟研究,模拟结果如图7 所示。可以看出,计算传质学模型预测值与实验测量的蛋白质浓度和固含率数据吻合较好,进一步证实了模型在流化床液固两相流动耦合传质模拟中的适用性。此外,采用双方程模型计算得到的Sct值在整个流化床内存在较大变化。这表明在流化床液固两相传质过程模拟中传统的恒湍流Schmidt 数Sct模型并不适用。而双方程模型可以直接确定湍流传质扩散系数,能更精确地预测组分浓度的分布。该模型的提出将为复杂液固两相流化床内传质过程的模拟研究提供有效途径。

图7 流动行为耦合传质过程的CFD模拟结果[51]Fig.7 CFD simulation results of flow behavior coupling mass transfer process[51]
4 结语与展望
流化床液固两相的流动和传质过程十分复杂,不仅有湍流流场的混沌特性,还伴随湍流传质扩散因素。当下数值模拟方法的快速发展为预测和分析流化床液固两相流动与传质过程问题提供了更为直观有效的途径。虽然一般认为液固两相流化系统因其两相的密度差较小,颗粒的分布比气固两相更为均匀,湍流的影响也相对较小。但已发表文献以及作者团队相关研究工作中均发现,液固两相体系中的流动及传质过程都存在显著的不均匀性,且传质过程受湍流影响也较为明显。近年来计算流体力学技术在流化床数值模拟中的应用大大提高了对流化床内流体流动特性及其流体力学特性的认识,对不同模拟条件下曳力模型的选取、模拟参数及边界条件设置等的探索已经较为深入,但在液固流化床内浓度分布预测方法方面的研究却相对较少。计算传质学方法在流化床液固两相流动耦合传质过程的模拟中展现出了独特的优势,采用双方程模型可以更加精确地预测流化床液固两相传质过程,但仍有许多工作有待进一步深入研究。
(1)流化床液固两相体系内流动、传递和反应过程的定量分析、评价标准、数学模型、模拟方法等还需扩展,如开展新的实验方法对速度场、浓度场等进行实时的检测和记录,搭建更为准确的计算传质模型,进一步完善流化床液固两相体系流动耦合传质过程的理论框架;
(2)液固两相体系的拓展,即将计算传质模型拓展到更为复杂的多相体系,如多种类型颗粒混合的液固体系或者气液固三相等体系中,丰富流动和传质的应用对象和研究内容;
(3)采用多尺度的模拟方法对单颗粒内部的传质情况进行更为准确的模型描述,且将流化床液固两相的模拟计算模型与工业应用相结合,促进对工业反应器设计、优化和放大,改善模型的准确性和适用性;
(4)液固传质过程特性细节的深入研究,流化床内的多相流相互作用过程以及流动行为直接影响传质组分质量的传递,可采用离散单元模拟颗粒内部的传质细节,考虑颗粒分布对传质过程的影响,进一步探索组分浓度分布与液固速度分布、流动结构的耦合规律。
符 号 说 明


