主结构提取和多尺度线性滤波的织物疵点检测方法

陈雪阳，潘 杨，朱 磊，翟子豪

(西安工程大学 电子信息学院，陕西 西安 710048)

0 引 言

在人工智能及机器视觉技术不断发展的今天，织物疵点检测自动化是学者们研究的重点方向。现存的有关织物疵点检测[1]方法可以分为统计法[2]、模型法[3-4]、显著性法[5-7]和深度学习方法[8-10]等4类。基于统计法的检测方法要提前构造和预估所需的特征参量信息，以便于通过参量信息分析研究图像中不同区域的统计差异，再利用统计差异为定位疵点提供可靠的依据。ZHANG等使用自相关函数将织物图像划分为子块，并利用平均值和标准差作为统计特征参数，将各子块的区域按有无疵点分为2类，对含有疵点的子块进行后处理实现疵点检测[11]。此类方法对单一纹理图像适用，泛化能力较弱，因此不适用于多类型的疵点。基于模型的检测方法通常是对织物的正常纹理进行建模，判断测试样本与模型是否一致，以此为依据实现疵点检测。COHEN等运用高斯马尔科夫随机场对无缺陷图像进行建模，将其分为大小相等的图像块，计算图像块与建模结果的相似值，判断图像块中是否含有疵点[12]。此类方法对单一纹理图像适用，泛化能力较弱。基于显著性的方法是以信息论和对比度作为基础，通过计算像素点的显著性值来获取疵点图像。ZHANG等提出借助多尺度分析提高疵点和背景的对比度，再利用颜色差异和位置距离共同测量缺陷值，最后通过阈值分割得到检测结果[13]。此类方法在检测图像中较为清晰的疵点时具有良好的表现，但对于模糊或者微小疵点的检测效果不理想。JING等对输入织物图像样本进行分解和贴标签，随后送入到CNN网络中进行训练学习，最后使用训练好的模型对整幅图像进行检测，得到疵点的类别和位置[14]。此方法在训练模型之前需要搜集和整理用于训练模型的织物数据集，但数据集样本存在着标签图像成本高、缺陷样本数量不足的问题，为后续疵点检测带来不便。

根据已有的织物疵点检测方法，不难发现有效抑制背景纹理对疵点检测尤为重要，因此本文采用的检测方法是通过预处理先初步抑制背景纹理，再利用改进的总变差 (total tariation,TV) 模型[15]对织物图像主结构进行提取，运用该模型实现对背景更精细的抑制效果,随后选用多尺度线性滤波器实现疵点增强,最后利用点乘运算与形态学处理得到完整的疵点区域。

1 织物疵点检测方法

为了进一步突出疵点区域，利用多尺度线性滤波器(Frangi)对疵点进行增强处理；最后利用预处理图和疵点增强图进行点乘运算和形态学处理。其流程如图1所示。

图 1 织物疵点检测流程Fig.1 The flow chart of fabric defect detection method

1.1 基于预处理和主结构提取的背景抑制

织物纹理是利用编织技术形成的具有一定分布规律的结构，它的结构特点通常表现为多样性和复杂性，这为织物疵点的检测带来挑战。因此消减或降低背景纹理中的信息，是有效克服疵点检测困难的重要方向和途径。

织物疵点和背景纹理之间的差别较小会增加疵点检测的难度，因此提高疵点和背景的对比度显得尤为重要。将RGB转换到HSV空间，通过提取明度信息(V)可以调整图像的亮度以及疵点和背景之间的对比度；再对提取V分量的图像进行中值滤波和对数增强以解决可能存在的噪声问题。该操作不仅可以去除噪声对疵点检测造成的不利影响，也可保留疵点区域边界信息，为后续的检测提供良好的基础，最终达到增强背景和疵点对比度的目的，其计算公式为。

(1)

式中：L为待检测织物图像；V为提取的明度分量。当L为彩色图像时，R、G、B分别为各颜色通道。预处理的图像可看作纹理与结构的融合，在疵点检测过程中，背景区域有时会被当作疵点进行处理，从而发生误检，影响疵点检测工作的效率和准确率。因此，对背景纹理信息进行弱化或者抑制是检测过程中必不可少的环节。TV模型[15]在消除纹理信息的同时也可提取结构信息，适应各向异性的纹理，具有较好的泛化能力。因此利用改进的TV模型获取织物图像的主结构[16]——疵点，最终削弱甚至消除预处理图像中背景纹理。

在预处理图像中的局部小窗口内，它的主结构成分中含有的相似性通常比在背景纹理复杂图像中的小窗口相似性要高，这也使得主结构更加突出。原模型公式为

(2)

式中：L和M分别为预处理图像和主结构图像；k是输入图像的索引号；ω为调整参数。第一项为保真项；第二项是正则矩阵。为了进一步增强织物图像的主结构部分和背景部分的差异，利用窗口总变差和窗口固有变差对式(2)中的正则矩阵(∇M)k进行改进，得到相对总变差模型公式，即

(3)

式中：改进后的第2项称为相对总变差；ω是调整参数，作用是控制改进公式中第1项和第2项之间的比例。改进项的具体表示为

(4)

(5)

(6)

式中：α的作用是控制窗口的空间尺寸，它取决于纹理的深浅程度。

相对总变差模型对预处理后图像的操作主要依赖于在图像中取得正方形窗口，在该区域内对于只包含背景的相对总变差值，该数值小于主结构所对应的总变差值。利用背景和主结构存在的差别实现对纹理背景信息的削弱，实验结果如图2所示。

(a) 预处理图 (b) 主结构图

为验证本文提出的背景纹理抑制性能，使用全局低秩分解抑制背景方法[17]和本文所提方法分别对输入织物图像进行处理，结果如图3所示。

(a) 输入织物图像

由图3可知，2种方法均可对背景纹理进行抑制，但使用预处理和主结构提取处理得到的结果显示背景纹理抑制效果更好。

实验过程中，相对总变差模型在实现过程中存在2个重要参量，即式(3)中的β和ω，β是避免分母出现0的情况，默认值为0.001；ω为控制平滑度参数。ω较小时，不能完整提取疵点部分；ω较大时，存在纹理细节丢失的情况。本文根据纹理的粗糙度和尺寸结构大小选择参数ω的范围为[0.4，0.6],实验验证结果如图4所示。

(a) 原始图 (b) ω=0.2 (c) ω=0.3

1.2 基于多尺度线性滤波的疵点增强

经过背景抑制后的织物图像其疵点区域仍存在不清晰的问题，为了获得更好的检测效果需进一步突出疵点区域。多尺度线性滤波器[18]可通过Herrsian矩阵各特征值来构造测量函数，对疵点进行精确定位，增强织物背景中的疵点部分，提高疵点区域和背景的对比度。对于主结构图像M，利用多尺度线性滤波器来描述织物结构时，需要利用图像在某点x0处邻域泰勒展开式[19]，即

(7)

式中：点x0以尺度σ得到的梯度向量是∇0,σ；Hessian矩阵是M0,σ。对主结构图像与高斯函数的导数进行卷积，可得

(8)

式中：γ为规则化的导数族，一般情况下，γ设为1。

式(7)中最后一项的二阶导数为

(9)

在织物图像中存在的疵点部分，通常来说灰度值大于背景部分对应的值，且疵点大多数都存在于细小区域内，式(9)中所指的二阶导数，疵点部分绝对值较大(或小)也说明了特征值较大(或小)，可表示为

(10)

且满足

(11)

多尺度线性滤波器在处理二维织物图像时，需要使用到二维矩阵Hessian所对应的2个特征值，分别是ω1和ω2(|ω1|≤|ω2|)。为了对织物图像背景纹理的像素进行区分，本文设置测度W进行表示。当疵点区域的背景纹理像素对比度低(或高)，相对应W的数值就较小(或大)，可表示为

(12)

由此可以推导出多尺度线性滤波器在处理二维织物图像时，所得到的测量函数，即

(13)

f0(γ)=maxF0(W)

(14)

式中：μ和c都是用来描述测量相似函数时所需的敏感性阈值参数，经实验验证可得μ=0.5，c=11；f0(γ)为不同尺度中的最大响应。

多尺度线性滤波器对提取到的疵点区域的边缘部分进行滤波增强，使得原本较为模糊的疵点部分不仅明显，也增强了疵点的局部细节信息，处理后的结果图如图5所示。

(a)主结构图 (b)多尺度滤波结果图

1.3 基于形态学处理的轮廓提取

织物图像经滤波器处理后其疵点区域虽得到明显增强，但背景部分仍存在细小区域未被消除且疵点轮廓不清晰。为了解决上述问题，需要完整刻画疵点区域轮廓。本文先将预处理结果图与疵点增强图像(二值图像)进行点乘运算并利用Canny算子提取疵点边缘，实现对边缘信息的获取并精细刻画疵点轮廓；疵点增强后的图像主要经过形态学中的膨胀、填充以及移除与边界连通目标的操作，实现孤立点去除最终获取完整的疵点区域，展示较好的可视化效果，能较好地保留疵点图像的边缘信息。结果图如图6所示。

2 结果与分析

为验证本文提出方法的有效性，将本文算法与基于鲁棒主成分分析模型方法(robust principal component analysis,RPCA)[20]、基于显著性检测方法(spectral residual,SR)[21]和基于最小二乘回归方法(prior knowledge guided least squares regression,PG-LSR)[22]进行对比，实验参数选用准确率和时间作为性能评价指标[23-25]。在实验过程中需要选取织物疵点样本作为数据集进行测试，数据集是在溢达织物裁片库中随机选取得到实验样本，数目为100，数据集样本先按照有无疵点进行分类，其中缺陷样本数目为50，无缺陷样本的数目为50；再按照纹理背景分为简单纹理和复杂纹理，其中包括油污、水污、破洞、带纱等疵点类型。

为了更好地说明每种方法的鲁棒性效果，对各方法中的参数设置进行实验与说明。在RPCA[20]检测算法中,主要参数是用于平衡疵点和噪声的λ和β，分别设置为λ=0.03、β=0.2；在SR[21]检测算法中，高斯滤波和均值算子的窗口设置分别为10×10 和3×3；在PG-LSR[22]检测算法中，权衡系数λ、随机块数s、重复次数k为3个关键参数，分别设置为：λ=0.75，s=5.0，k=5.0；本文在改进的TV模型中有2个参数，分别是描述纹理元素尺寸的参数β和控制平滑度参数ω。取默认值为β=0.001,ω=[0.4,0.6]。各方法对测试样本进行检测，实验验证结果如图7、8。

图7和图8分别针对简单和复杂纹理背景的织物图像进行检测，图中分别展示了3种对比算法和本文提出方法的检测结果。图7(a)为原始输入图像，其中第1～3幅均含有较为清晰的疵点，第4幅含有较细小的疵点，第5幅是未含有疵点的正常样本图像。

(a) 多尺度滤波结果图 (b) 提取轮廓图 (c) 疵点图

由图7、8的实验结果可以看出，文献[20]和文献[22]的检测方法均可准确检测出疵点位置，但文献[20]的检测结果仍有未消除的背景纹理，文献[22]的检测结果中存在疵点轮廓模糊的情况；文献[21]的检测结果对疵点位置信息判断有误，疵点形状不完整；以上3种检测方法对未含有疵点的织物图像都存在误检情况。本文提出的方法在保证准确检测疵点的同时也可得到完整疵点轮廓，并且对正常织物图像没有出现误检情况。

表1为各方法对测试集图像检测后得到的参数比较。从准确率和时间2个参数比较来看，本文方法的准确率比其他3种算法提高了9%以上；检测时间居于第2，仅次于文献[20]中的检测方法。

(a) 输入图像

(a) 输入图像

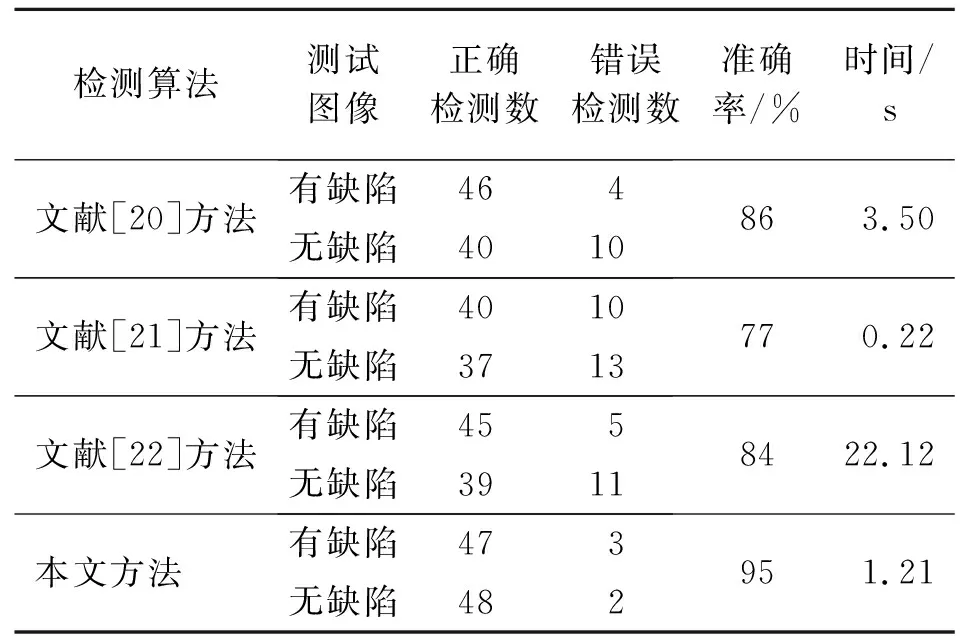
表 1 检测结果的参数比较

从上述实验结果可得出，本文采用改进的TV模型在抑制背景纹理的同时提取主结构，可以有效提升疵点检测效率和准确率。

3 结 语

本文提出了基于主结构提取和多尺度线性滤波的织物疵点检测方法，首先通过图像预处理和改进的总变差模型，削弱了背景纹理对疵点检测的影响，然后利用多尺度线性滤波处理有效增强了疵点区域，最后提取轮廓结合形态学处理有效分割出了疵点区域。由于本文采用先抑制背景纹理，为后续疵点图像的增强提供良好的基础，最终实现对疵点轮廓的精准提取，使得检测准确率得到明显提升。