带临界项的分数阶薛定谔-泊松系统的非平凡解
2022-01-26冯晓晶
张 炫,冯晓晶
(山西大学 数学科学学院, 山西 太原 030006)
1 引言与主要结果
薛定谔-泊松系统广泛地出现在量子力学和半导体理论中。根据经典模型, 带电粒子和电磁场的相互作用可以通过非线性薛定谔方程耦合泊松方程描述。文献[1]研究了薛定谔麦克斯韦方程, 文献[2]研究了模拟电磁波在等离子体中传播的薛定谔方程。近年来, 由于分数阶拉普拉斯算子被广泛研究和应用在金融、优化、反应扩散等许多领域中, 因此分数阶薛定谔-泊松系统受到许多数学家们广泛关注。近几年来, 许多数学家研究了如下薛定谔-泊松系统
(1)
解的存在性和多重性, 其中x∈R3,V、K、f是连续函数。此后,学者们对系统(1)在V、K、f的不同假设下展开深入研究[3-6]。当V(x)≡1,
f(u)=|u|p-1u(1 时, 文献[3]研究了系统(1)解的存在性和不存在性;当f是周期渐近线性函数且满足单调性条件, 文献[4]运用Nehari流形方法获得系统(1)基态解的存在性, 且当f是奇函数时, 得到了系统(1)有无穷多解的存在性。 最近,临界分数阶薛定谔-泊松系统被广泛关注[7-10]。例如许多文献研究了如下分数阶薛定谔-泊松系统: (2) (3) 利用集中紧性原理和变分方法得到了其基态解的存在性。 本文主要目的是研究具有双临界项的分数阶薛定谔-泊松系统 (4) (5) 记Br为以0为中心, 以r为半径的闭球, 即Br={u∈Ds,2(R3):‖u‖≤r};记∂Br={u∈Ds,2(R3):‖u‖=r}。用C>0表示不同的正常数。由Lax-Milgram定理,∀u∈Ds,2(R3),系统(4)的第2个方程有唯一解φu∈Ds,2(R3)。将φu代入到系统(4)的第1个方程, 则系统(4)变为方程 (6) 方程(6)相应的能量泛函为 ∀u,v∈Ds,2(R3),Iλ(u)∈C1(Ds,2(R3),R),成立 为了证明主要结果,先给出以下引理, 然后利用在球上的Ekeland变分原理证明系统(4)有一个能量严格小于零的非平凡解,以及应用山路定理证明系统(4)有另一个能量严格大于零的非平凡解。 引理1[11]下列性质成立: 1) ∀u∈Ds,2(R3),φu≥0; 3) ∀u∈Ds,2(R3), 4) 若un在Ds,2(R3)中弱收敛于u, 则存在子列, 使得φun在Ds,2(R3)中弱收敛于φu。 时, 使得Iλ满足(PS)c条件, 其中 证明设{un}⊂Ds,2(R3)为Iλ的(PS)c序列, 则当n→∞时,有 (7) 由式(7)知 (8) 因为un(x)→u(x),a.e.x∈R3,且 故 结合式(8),有 因为un(x)→u(x),a.e.x∈R3,且 即 利用式(7), 则 (9) (10) 由式(9)和式(10), (11) 由 和式(11)得 不失一般性,假设当n→∞时,an→a,bn→b。注意到, 当n→∞,得到 一方面, 由Hölder不等式和Young不等式, 根据式(9)得 另一方面, 由式(7)和式(11),有 这是矛盾的。故l=0, 因此在Ds,2(R3)中un→u。证毕。 证明∀u∈Ds,2(R3), 有 令 根据文献[14]中引理3.3,存在常数 使得 Iλ|‖u‖=R>0 显然, 下式 于是, 当t充分小时,有Iλ(tφ0)<0。因此, 存在充分小的u, 使得Iλ(u)<0, 即 (12) 证毕。 引理5假设λ∈(0,Λ0), 对给定的R, 泛函Iλ满足下列的条件: 1) 若‖u‖=R, 则Iλ(u)>0; 2) ∃e∈Ds,2(R3), 当‖e‖>R时, 使得Iλ(e)<0成立。 证明1) 当λ<Λ0时, 由引理4易知结论成立。 2) ∀u∈Ds,2(R3){0},有 当t→∞时,Iλ(tu)→-∞。因此,∃e∈Ds,2(R3), 当‖e‖>R时, 使得Iλ(e)<0成立。证毕。 定义 uε=η(x)Uε(x) 有下面的估计[14-15]: 其中Kp为正常数。 引理6[14]设 当ε→0+,有 证明当t→∞时, 有Iλ(tuε)→-∞, 则∃tuε>0, 使得 ∀t≥0,下式 令 从而根据引理6,下式 因此, 当λ∈(0,min{Λ0,Λ1})时,有 证毕。 为了方便,令 证明显然, 当0<λ<λ*时, 引理1、3、4,定理2、引理5和引理7都成立。应用山路定理[16], 存在序列{un}⊂Ds,2(R3),且 其中 和 Γ={γ∈C([0,1],Ds,2(R3)): γ(0)=uλ,γ(1)=e} 定理1的证明:根据定理2和定理3,则对充分小λ*>0, 当0<λ<λ*, 系统(4)至少有2个非平凡解。证毕。 通过应用Ekeland变分原理和山路定理的方法,证明了分数阶薛定谔-泊松系统非平凡解的存在性和多重性。由于所研究的系统具有双临界项和扰动性,因此对于估计非紧性水平以及相应泛函的能量在非紧性水平之下具有一定的困难;除此之外,对(PS)条件的成立也具有一定难度。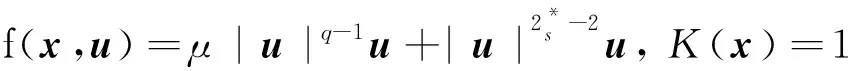
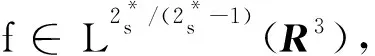
2 预备知识
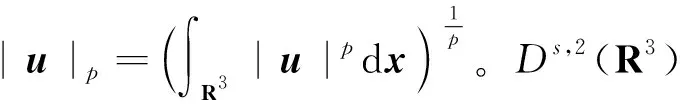
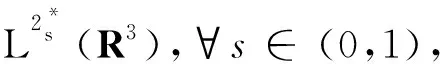
3 定理1的证明
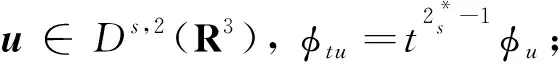
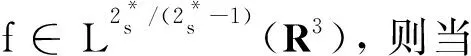
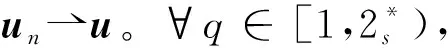
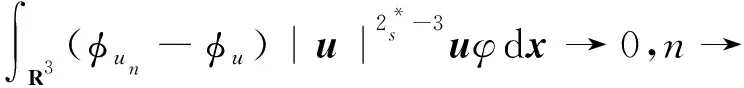
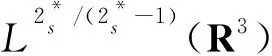
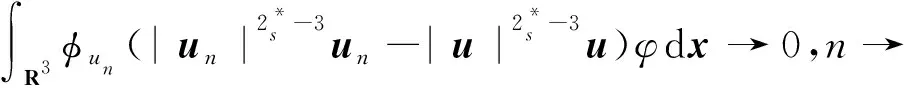
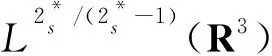
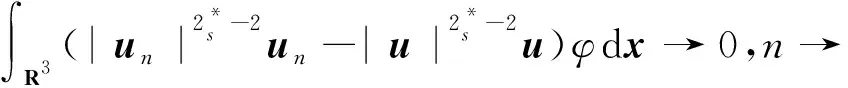

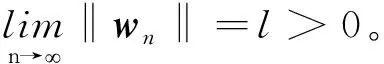
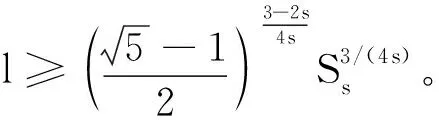
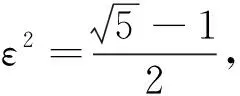
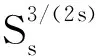
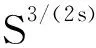
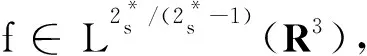
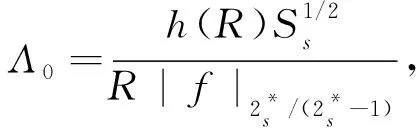
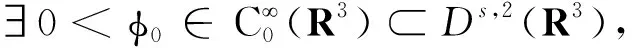
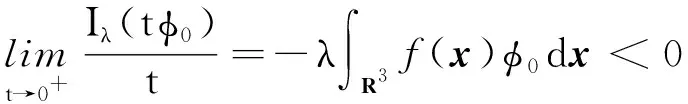
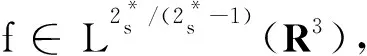
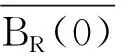
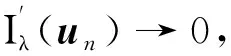
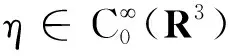
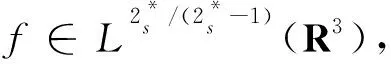
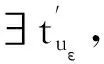
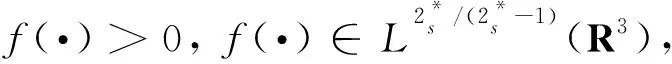
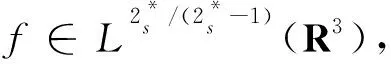
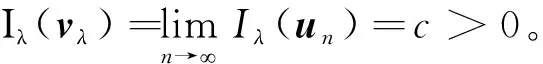
4 结 语
