融合正弦余弦和种群初始化策略的布谷鸟算法

张珍珍，贺兴时，于青林，杨新社

(1.西安工程大学 理学院,陕西 西安 710048；2.汤普森大学 数学与统计学院,加拿大 甘露 V2C0C8；3.密德萨斯大学 科学与技术学院,英国 伦敦 NW4 4BT)

0 引 言

元启发式算法包括花授粉算法[1](FPA)、蝙蝠算法[2](BA)、鲸鱼优化算法[3](WOA)、蚁群算法[4](ACO)、粒子群优化算法[5](PSO)、萤火虫算法[6](FA)等。这些生物算法仿照动物行为特征，灵活高效地解决了许多复杂优化问题。

布谷鸟搜索算法[7](cuckoo search，CS)广泛应用于智能机器人[8]、水利工程[9]、物流配送[10]、电力设计[11]、优化聚类[12]、神经网络[13]等领域，但布谷鸟算法仍存在寻优解结果不够精确，求解速度不够快和容易取得当前最优解而无法继续迭代寻找全局最优解等方面的问题。为了改善布谷鸟算法存在的这些问题与不足，人们对布谷鸟算法做出了相应的改进。2013年，OUYANG等提出了离散布谷鸟搜索算法(DCS)，并将其应用到经典问题旅行商中[14]；2018年,BOUSHAKI等提出了一种新的量子混沌CS算法(QCCS)，将混沌映射及量子技术与布谷鸟算法结合[15]；2019年，宋庆庆等将拟牛顿算法和布谷鸟算法结合，建立了一种拟牛顿布谷鸟混合算法[16]；2020年，王晓华等改进了布谷鸟算法的发现概率步长[17]。

针对布谷鸟优化算法在处理复杂函数时，寻优结果不精确、寻优速度不高和容易陷入局部最优解等问题，本文提出了融合正弦余弦和种群初始化策略的布谷鸟算法(DCCS)。首先，在布谷鸟初始种群产生环节引用一种结合均匀化与随机化的策略，以半均匀、半随机的方式产生初始种群，有效地减少随机误差，提高了算法寻优效率。其次，分别在全局搜索和下一步局部搜索中引入了正弦余弦算子，充分灵活开发上一代鸟窝位置作用，克服算法易陷入局部最优的缺陷，提高算法寻优搜索能力。最后，引入了指数型动态概率p代替固定概率，用于自适应平衡算法的2个阶段。实验结果表明，DCCS算法提高了结果精度和运算效率，在一定程度上具有更好的寻优性能。

1 布谷鸟优化算法

基本布谷鸟算法包括莱维飞行和随机偏好游走过程，莱维飞行位置更新公式[18]为

(1)

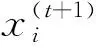
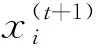
(2)

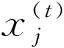
2 改进的布谷鸟优化算法

2.1 种群初始化策略

布谷鸟算法的初始种群是随机分布产生的。这种随机分布方式会致使寻优结果含有随机误差，在一定程度上影响了布谷鸟算法的寻优精度; 并且因为种群分布随机混乱，没有规律地分布在解区间，也在一定程度上影响了布谷鸟算法的寻优速度。为了解决因为布谷鸟初始种群完全随机分布而对布谷鸟算法性能的影响问题，在布谷鸟初始种群产生环节引用一种结合均匀化与随机化[19]的策略。以半均匀、半随机的方式产生初始种群：一方面保证均匀化，将布谷鸟算法的解变量分布区间平均分割，有规律地进行迭代搜索，帮助提高算法的寻优速度和寻优精度；另一方面保证随机化，随机地选取被划分区间和在被划分区间中选取随机值，保证了算法的初始随机性。种群初始化的具体方法[19]如下:

1) 输入种群规模n，决策向量维度k，各决策变量xj(j∈{1，2，…，n})的区间[aj,bj]。

2) forj=1,2,…,k。

3) Δj={[aj,aj+Δj],(aj+Δj,aj+2Δj],…,(aj+(n-2)Δj,aj+(n-1)Δj],(aj+(n-1)Δj,bj]}。

4) fori=1,2,…,n。

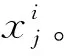
6) 更新集合Δj，从集合Δj中删除在5)中已选中的子区间。

7) end for。

8) end for。

9) 输出多样性的初始种群。

通过对布谷鸟算法采取基于均匀化和随机化相结合的种群初始化方式，在保证算法初始种群随机性的前提下，获得了一组在决策区间均匀分布的初始解，减少了算法因为初始解分布完全随机而降低的运算速度和产生的随机误差，提高了算法的运算效率和寻优速度。

2.2 融合正余弦算子

在布谷鸟算法中，上一代鸟窝位置发挥重要作用，不断引导算法向最优解靠近。但在布谷鸟算法的莱维飞行阶段和偏好随机游动阶段的更新公式中，都将该位置固定，这种更新方式容易造成算法在迭代过程中取得局部最优而非全局最优，致使种群出现停止搜索的现象，无法获得全局最优解。为了克服这一缺陷，平衡布谷鸟算法的全局搜索和局部搜索，在布谷鸟算法的全局搜索和局部搜索阶段的上一代鸟窝位置处引入正弦和余弦算子[20]。通过正余弦算子随迭代次数的变化，灵活调整布谷鸟鸟窝的位置：使其前期保持灵活性，进行全局搜索；后期布谷鸟个体趋于局部开发，进行精细搜索，使算法取得全局最优解。融合正余弦算子后的全局搜索公式和局部搜索公式分别更新为：

(3)

(4)

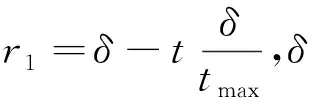
r1sinr2、r1cosr2共同控制算法进行全局搜索和局部搜索。当r1sinr2、r1cosr2的值>1或<-1时，上一代鸟窝位置的惯性权重较大，有利于扩大搜索范围，开发不同区域，提高布谷鸟算法的全局开发能力，避免算法只取得当前最优解而无法继续迭代寻找全局最优解; 当r1sinr2、r1cosr2的值在1和-1之间时，上一代鸟窝位置的惯性权重系数取值较小，不再进行大范围搜索，以免跳出最优范围，而是在最优解附近进行精细搜索，直至寻找到全局最优解。将正余弦算子引入到布谷鸟算法中，使上一代鸟窝位置具有灵活性，提高算法性能。

2.3 指数型动态发现概率

在布谷鸟算法中，用来控制全局搜索和偏好随机游走过程的概率为固定数值P=0.25。概率P是布谷鸟算法转换莱维飞行阶段和偏好游走阶段的重要参数，固定概率值不利于灵活转换算法的2个阶段，无法随迭代进程及时调整算法的全局探索和局部开发进程。本文引入了指数型动态切换概率P代替固定概率，使概率P随着迭代次数的变化自适应调整算法的2个阶段，改善因固定概率P而影响的算法性能。动态概率公式如下：

(5)

式中:Pmin是当前概率的最小获得值;Pmax是当前概率的最大获得值;t是当前迭代的次数;tmax是迭代的次数最大值;β(0,1)是定义在(0，1)的贝塔分布;φ是极小的数，用于调整发现概率和期望值之间的偏差程度。指数型动态概率变化图如图1所示。

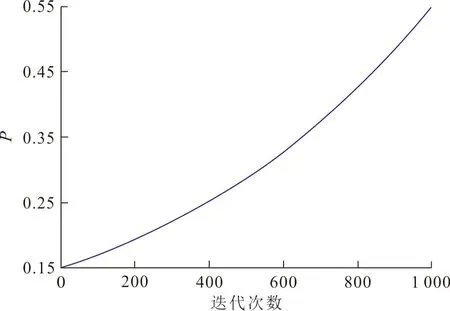
图 1 指数型动态概率变化

由图1可以看出，提出的概率P是随着迭代过程自适应指数型增大的动态发现概率。在布谷鸟算法搜索前期，概率P的取值在0.2左右，较小的概率取值在控制全局搜索和局部搜索的切换过程中，控制算法在搜索前期多进行大范围的全局搜索，不断使算法结果跳出当前局部最优解，避免算法在一开始就陷入局部最优而停止搜索。随着搜索过程的不断进行，概率P的取值也在不断增大，直至在算法搜索后期，概率P的取值超过了0.5，较大的概率取值将控制算法在搜索进程后期时不再进行大范围搜索，而是在靠近全局最优解的小范围内进行细致搜索，直至寻找到最终全局最优解。通过在布谷鸟算法中引入指数型动态发现概率，概率P与搜索过程动态联系在一起，自适应平衡算法的2个阶段进程，提高了算法的整体寻优性能

2.4 DCCS算法执行步骤

DCCS算法执行步骤如下：

1) 设置布谷鸟算法各个参数值：m为鸟窝个数，n为维数，N为迭代次数最大取值。依照式(5)设置发现概率P，计算m个鸟窝的适应度值。

2) 初始化种群，生成均匀化与随机化相结合的初始种群。

3) 按照式(3)更新布谷鸟鸟窝位置，并计算每个更新解的适应度值。当更新解的适应度值更高时，用适应度更高的解替换旧的解；否则，仍使用旧的解。

4) 按照式(5)的动态发现概率P剔除部分解，并用改进后的式(4)产生新解。新解数量与剔除的部分解相同，进行局部搜索。

5) 计算m个鸟窝的适应度值，得当前最优解。

6) 判断算法是否达到迭代次数N。若达到，输出当前最优解; 若没达到，重复2)～6)。

3 仿真实验

为了验证融合正弦余弦和种群初始化策略的布谷鸟算法(DCCS)的寻优性能，选取了6个不同难度的函数，分别测试DCCS算法的收敛速度、收敛精度，同时与ASCSA、CS、BA、FPA等4种算法进行对比分析。6种测试函数如表1所示。

表 1 测试函数

3.1 测试环境及算法参数

实验环境如下：CPU为i5-4288U 2.60 GHz，运行内存4 GiB;操作系统Windows10;编程环境Matlab r2020a。DCCS算法及ASCSA、CS、BA、FPA算法参数设置如表2所示。

表 2 算法参数设置

3.2 算法求解精度比较

表3～8分别给出了5种算法对测试函数f1(x)～f6(x)，在维数n为10、100条件下的方差、最优值、平均值及最差值等4个指标的测试结果。其中，f1(x)函数是典型的非线性多模态函数，极小值个数与维数成正比且起伏不定。从表3中可以看出：DCCS 已经展现出良好的全局性能,取得了一个全局最优的值,而其他4种算法后期都已经陷入局部最优。f2(x)～f3(x)为复杂多峰函数，在整个解空间内存在多个极值点，可以考察该算法是否具备优秀的寻优能力，能否在取得当前最优值后继续迭代得到全局最优值。由表4～5可以看出：ASCSA等4种算法都陷入了不同程度的局部最优，并未继续寻找到全局最优解0，而DCCS算法在各个维度条件下都取得了相对应函数的最优求解，通过对比优势突出。f4(x)～f6(x)为单峰函数，在整个解空间内只有一个极值点。由表6～8可以看出：DCCS在处理单峰函数时仍能取得全局最优解，表现出良好的稳定性。综上所述，与其他4种算法相比，DCCS算法寻找全局最优解优势更明显，不易陷入局部最优，并且在高维条件下结果也未改变，寻优性能稳定。

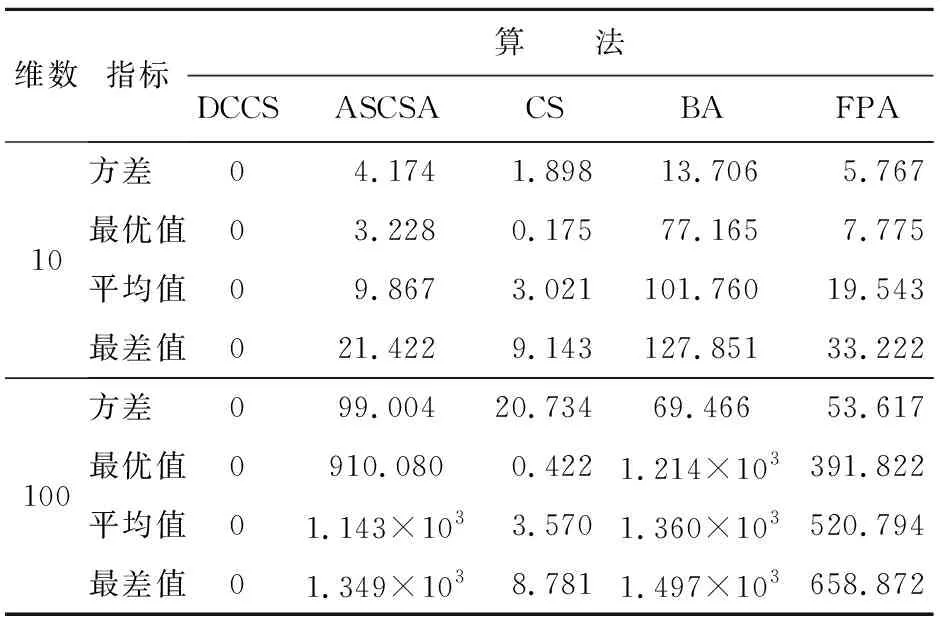
表 3 f1(x)函数仿真结果

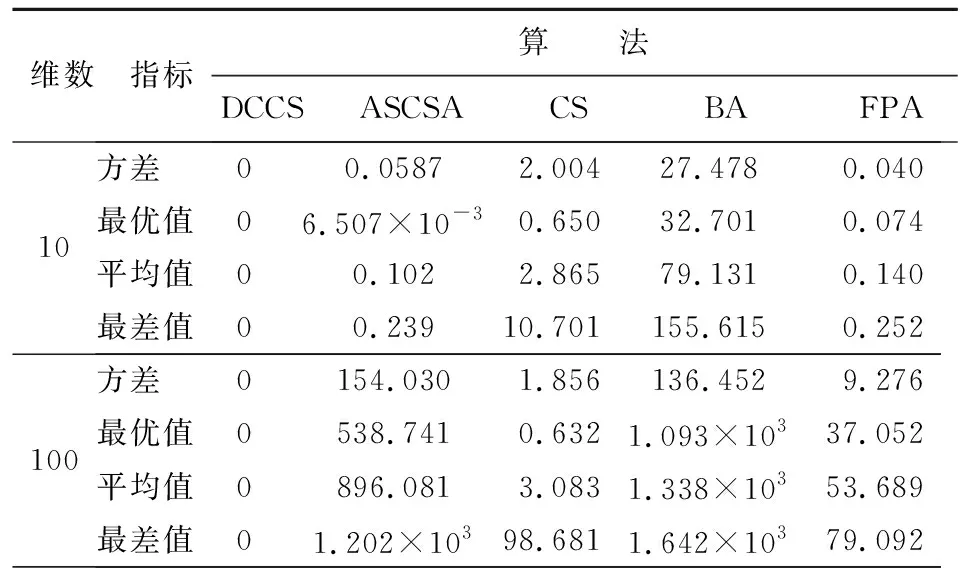
表 4 f2(x)函数仿真结果

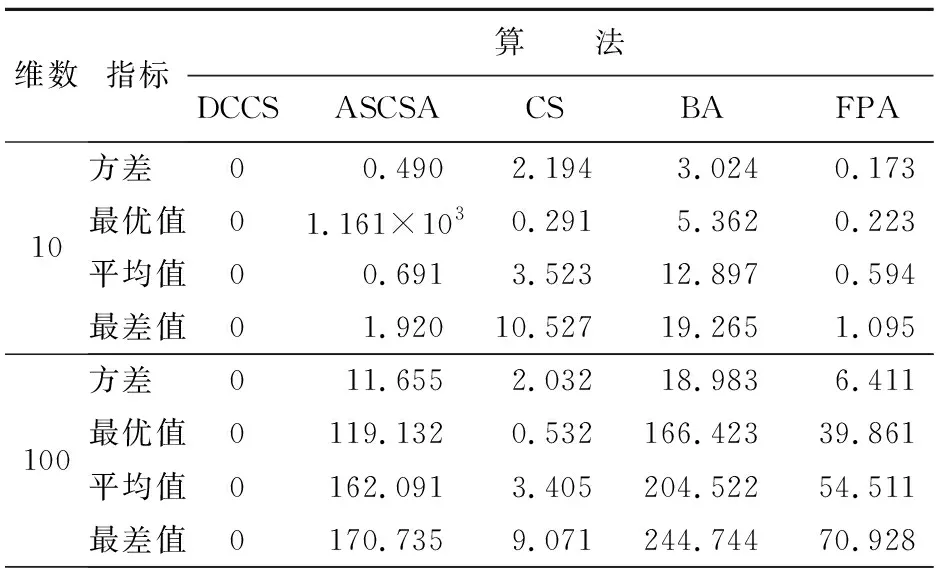
表 5 f3(x)函数仿真结果

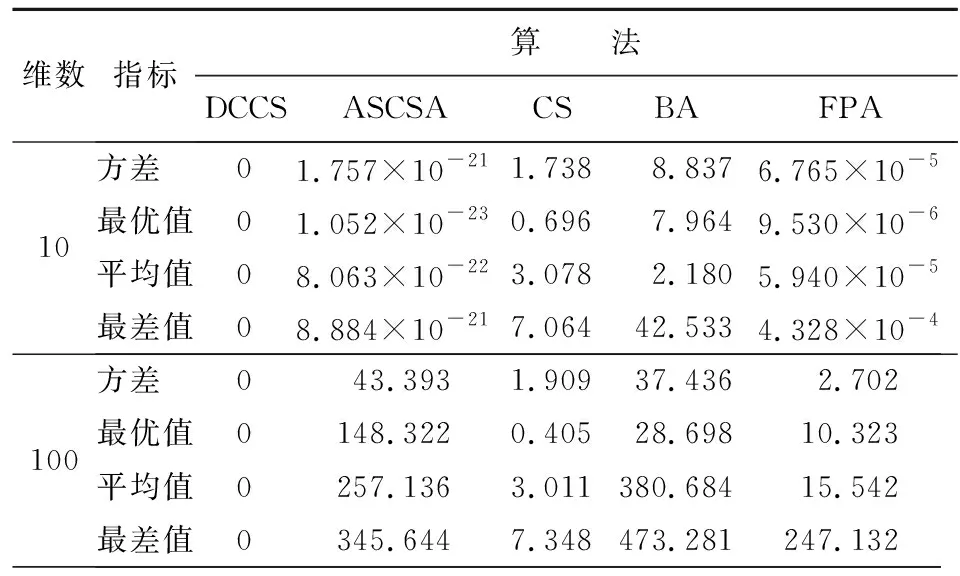
表 6 f4(x)函数仿真结果

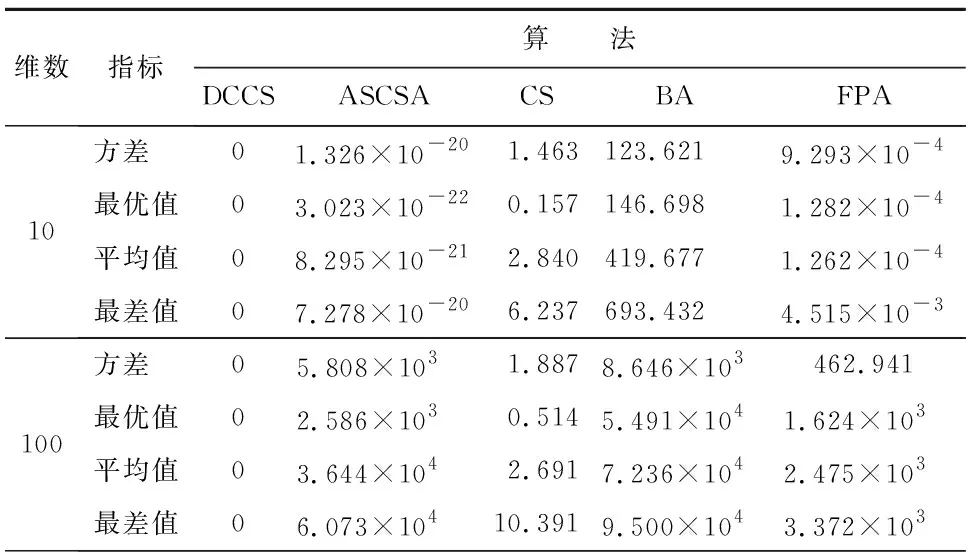
表 7 f5(x)函数仿真结果

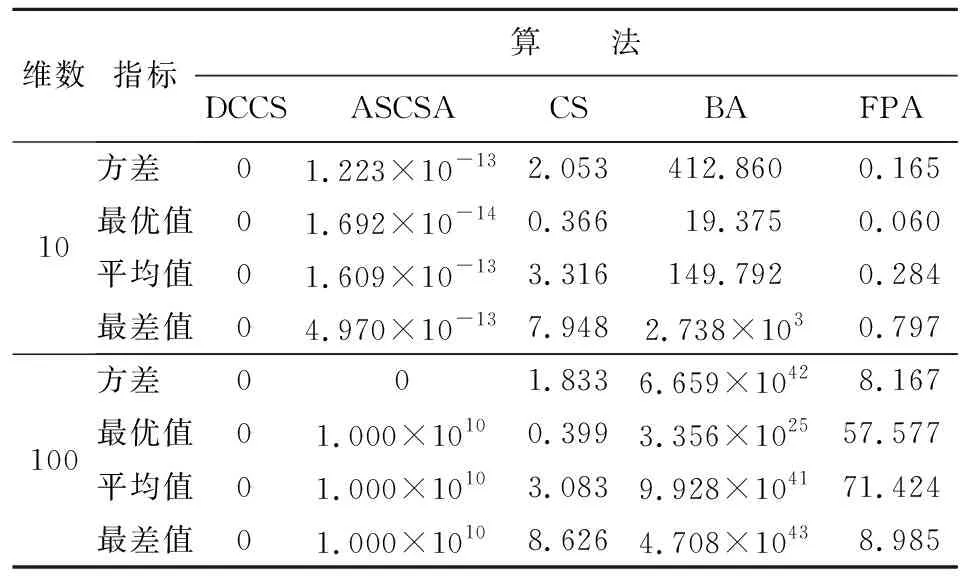
表 8 f6(x)函数仿真结果

3.3 算法收敛性

图2～7分别是改进后的布谷鸟算法与其他4种算法在6种函数下的收敛曲线图。其中f1(x)～f3(x)为多峰函数，在整个解空间存在不止一个极值点，可以考察算法的寻优能力，能否在取得当前最优值后继续迭代得到全局最优值。由图2、4可以看出：在其他4个算法迭代后期都未能取得全局最优时， DCCS算法在50次迭代左右就取得最优值。由图3可以看出：BA算法陷入了局部最优，其他算法分别在200至800次后才取得最优值，而DCCS算法在一开始就达到了全局收敛，取得了最优值。f4(x)～f6(x)为简单单峰函数，在整个解空间只有唯一一个极值点，可以考察比较算法的寻优速度。由图5～7可以看出：ASCSA等4种算法有时在100次迭代以后搜索到最优求解，或者在1 000次迭代结束后都未搜索到最优求解，而DCCS算法在搜索前期却快速搜索得到各个函数的最优求解，收敛速度优势明显。综上所述，与ASCSA等4种算法对6种函数的搜索结果相比较，DCCS算法具有相对较高的寻优速度，有效地改善了布谷鸟算法收敛速度慢的不足。

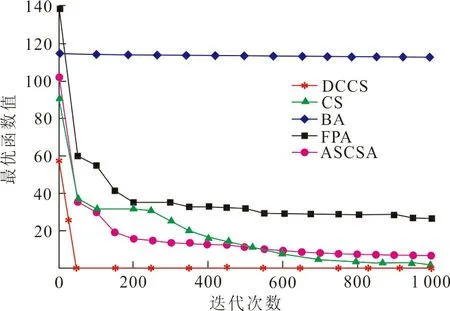
图 2 Rastrigin函数收敛曲线Fig.2 Convergence curve of Rastrigin function

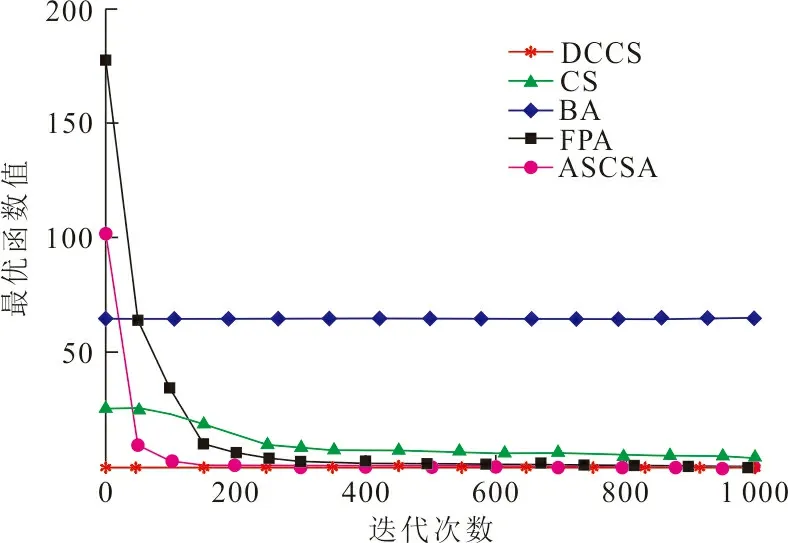
图 3 Griewank函数收敛曲线Fig.3 Convergence curve of Griewank function

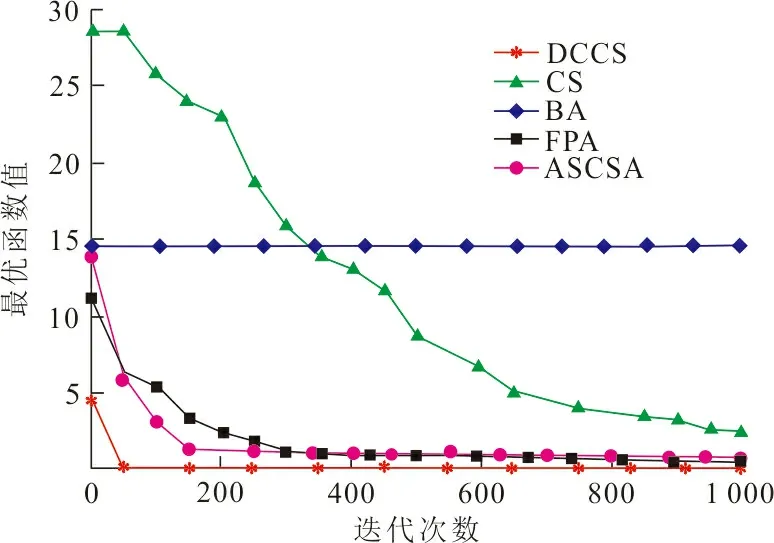
图 4 Alpine函数收敛曲线Fig.4 Convergence curve of Alpine function

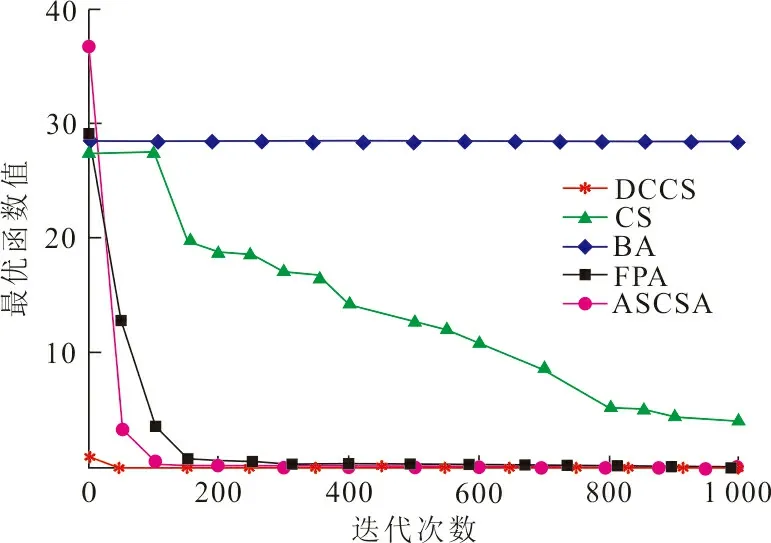
图 5 Sphere函数收敛曲线Fig.5 Convergence curve of Sphere function

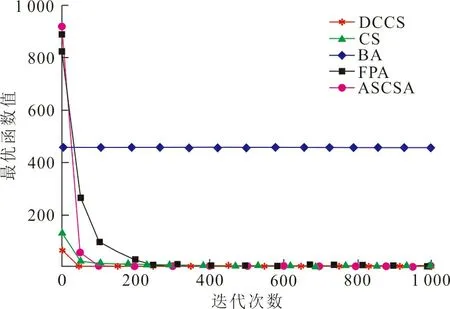
图 6 Sum square函数收敛曲线Fig.6 Convergence curve of Sum square function

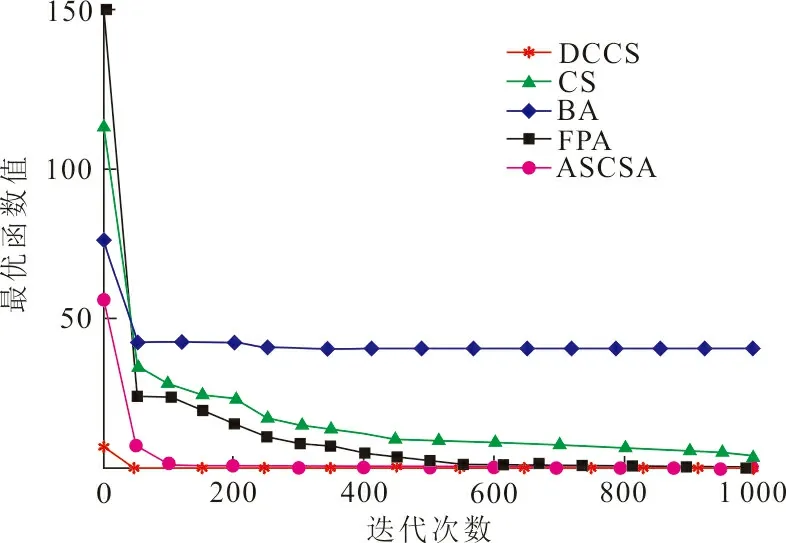
图 7 Schwefel函数收敛曲线Fig.7 Convergence curve of Schwefel function

4 结 语

本文提出了融合正弦余弦和种群初始化策略的布谷鸟算法。着眼于对布谷鸟算法进行整体优化，充分协调利用种群初始化策略，正余弦算子和指数型动态概率P三者之间的关系。在算法初始阶段，对布谷鸟初始种群利用结合均匀化与随机化的策略，在保证种群随机性的前提下，使初始种群随机分布在解区间; 在算法的莱维飞行阶段和偏好游走阶段，引入变化范围在[-1,1]的正余弦算子，灵活调整上一代鸟窝位置;通过引入指数型动态概率P，确保P在整个迭代阶段保持在[0.15,0.55]区间的动态变化状态，动态平衡算法的2个阶段。3个策略之间相互作用、相互联系，共同作用于布谷鸟算法。与另外4种算法相比较并通过6个测试函数的仿真结果表明：融合正弦余弦和种群初始化策略的布谷鸟算法，在一定程度上提高了算法性能，加快了寻优速度，提高了寻优解的数量级精度。