机械光栅式测缝计应用于无砟轨道板上拱监测的可行性分析
2022-01-26张利刚
张利刚,高 山
(西南交通大学 地球科学与环境工程学院,成都 611756)
目前,我国已经成为高速铁路发展最快、规模最大的国家,并且已经形成一套成熟的无砟轨道体系[1]。鉴于我国地域广阔,南北地区气候差别大,这使得作用于无砟轨道的温度力更为复杂,在温度力的反复作用下,无砟轨道的变形主要包括轨道结构随温度变化而产生整体性的伸缩变形和由轨道板厚度方向上温度梯度造成的轨道板翘曲变形。随着时间的发展,在温度力和列车荷载的反复作用下,无砟轨道结构会产生各种各样的病害,如轨道板与砂浆层离缝、宽窄接缝处损坏和轨道板非预裂缝处贯通裂纹等,如图1所示。这些病害会破坏无砟轨道的结构稳定性,引起轨道板上拱,影响铁轨面的平顺性,严重时会危害到铁路的安全运营,因此无砟轨道结构稳定性监测十分必要[2-4]。
当前我国对轨道板上拱离缝的检测主要是依靠现场检查、肉眼观察,如图2所示;而对于变形较大的重点地段,采用常规水准测量的方式进行监测,这种方式不但有严重的滞后性而且费时费力,难以在有限的天窗时间内完成辖区内轨道结构的全覆盖检查。而在无砟轨道板上拱离缝的自动化监测方面尚且没有成熟的方案可供借鉴引用,基于此对机械光栅式测缝计应用于无砟轨道板上拱自动化监测的可行性进行研究分析。

图1 无砟轨道板典型病害示意图

图2 轨道板上拱离缝检测示意图
机械光栅式测缝计即光栅位移传感器,是一种高精度的位移测量设备,它具有高精度、大量程、高分辨率和抗干扰能力强的特点,主要应用于数控机床、航天卫星、精密仪器制造和冶金等领域[5]。在光栅位移传感器的研发方面,国外一些发达国家走在技术发展的前沿,推出多代光栅位移传感器,传感器的信噪比和测量精度也得到很大程度的提高[6]。我国关于光栅式位移传感器的研究较西方发达国家还有一定的差距,但长春光机所等多家单位都开展光栅位移传感器的研究工作,打破国外垄断[7]。随着科学技术的不断发展,光栅位移传感器已应用到重大工程的建设与监测、精密设备安装等多个领域。
1 测量原理
机械光栅式测缝计一般由光源、聚光镜、主光栅、指示光栅和光电器件等部分组成,如图3所示。光源的光线通过聚光镜变成平行光束,照射到光栅尺上,标尺光栅与指示光栅间的相对位移通过光电器件转化为数字信号进行后处理。在工作时,标尺光栅固定在传感器上不动,而指示光栅与相对运动的机械部件相连,当机械部件移动时就会带动指示光栅的相对运动,通过光栅的光束就会发生干涉和衍射现象,产生莫尔条纹,莫尔条纹通过光电器件转化为正弦变化的电信号。指示光栅每移动一个栅距,光电器产生的电信号就变化一个周期;对这些周期性变化的电信号进行后处理即可得到标尺光栅和指示光栅的相对位移量[6,8]。
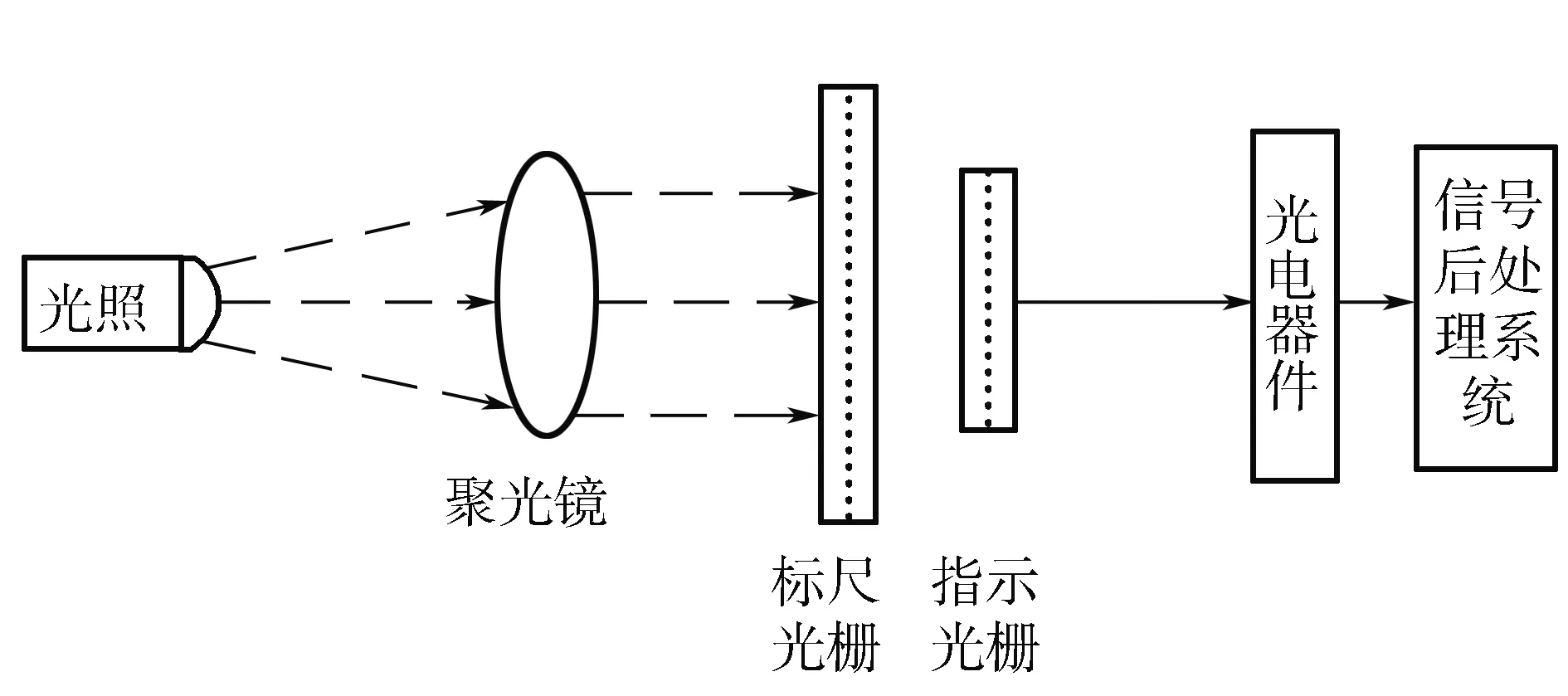
图3 光栅测缝计原理示意图
莫尔条纹的形成原理如图4所示,不妨设标尺光栅的栅距为B1,指示光栅的栅距为B2,实际上指示光栅与标尺光栅间留有细小间隙,且两者的光栅线间成很小的夹角θ。当平行光束照射到光栅上时,根据光线的遮光原理,在d-d线上透光效果最佳,会形成一条光带;而在f-f线上透光效果最差,会形成一条暗带。图4(a)中黑白相间的条纹即为莫尔条纹,其为光栅测量的基础。图4(b)中W为莫尔条纹的间距,平行四边形四边AB,BC,CD和AD分别代表图4(a)中交叉相邻的4根条纹,其中A点至BD的垂直距离即为莫尔条纹的间距W;AB至CD的距离为标尺光栅的栅距B1,BC到AD的距离为指示光栅的栅距B2,AB与CD的夹角即为两栅线间的夹角θ[9]。
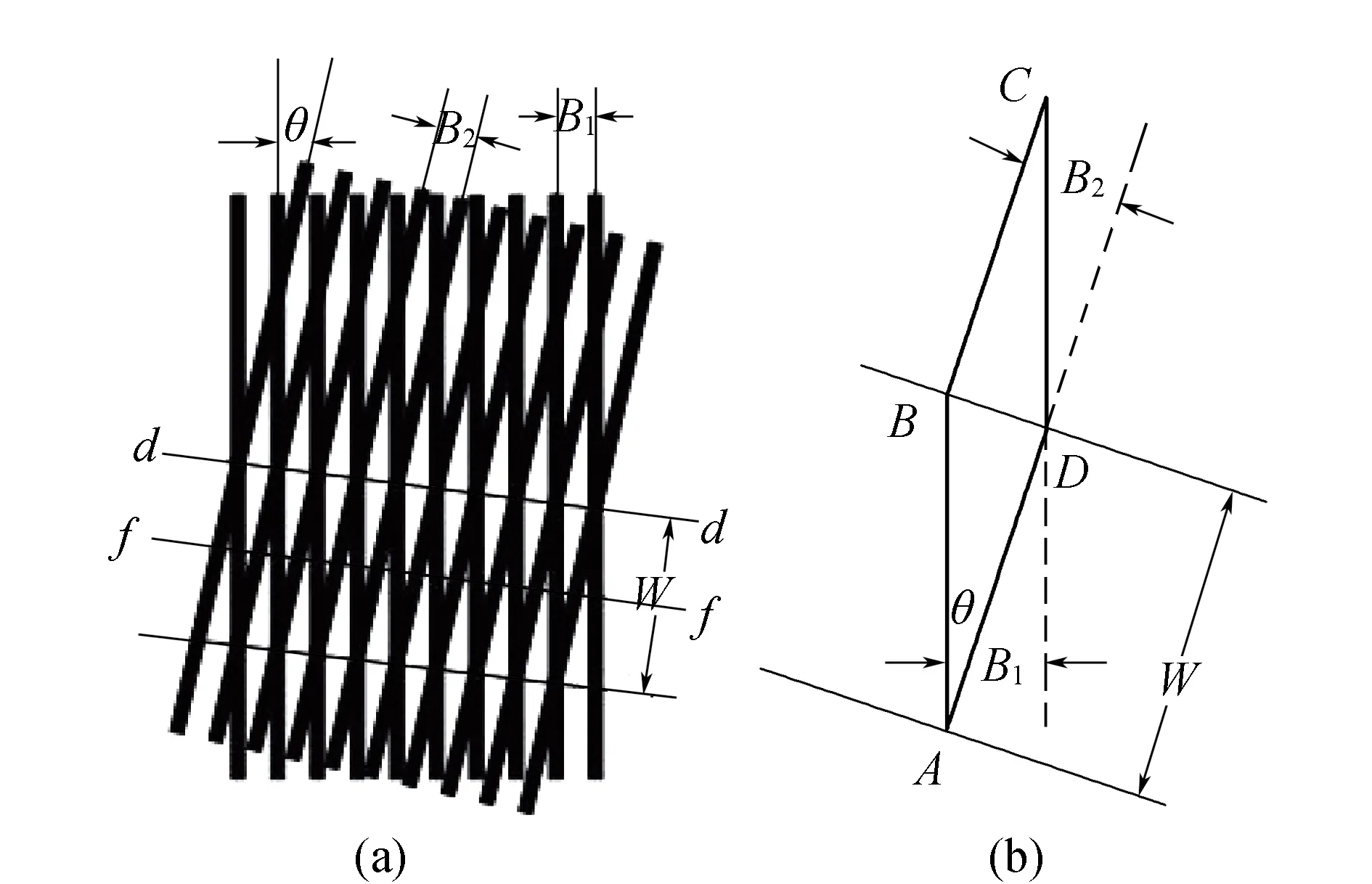
图4 莫尔条纹形成原理示意图
根据平行四边形的面积算式可得:
AB×B1=AD×B2=BD×W.
(1)
根据余弦定理,在三角形ABD中,
BD2=AB2+AD2-2AB×ADcosθ,
(2)
综合式(1)、式(2)可得:
(3)
当标尺光栅与指示光栅的栅距相等,即B1=B2=B时,莫尔条纹的间距W可表示为:
(4)
当标尺光栅与指示光栅相对运动时,黑白条纹便会移动;当指示光栅运动一个栅距B时,黑白条纹也会移动一个条纹间距W,光电器件会接收到一个光强变化周期,输出一个电信号,计数器加1;光栅测缝计正是基于这一原理来进行相对位移的测量。
2 误差分析
结合机械光栅式测缝计自身的结构特点,误差因素主要包括:各部件本身的特性、加工工艺、安装误差和外界环境的影响;基于此,光栅测缝计的测量误差可归纳为4类:光源误差、光栅误差、电路误差和环境误差[10-14]。
1)光源误差。光栅测缝计理想的光源应是光强和波长恒定的单色平行光,但碍于客观条件,光源的波长和功率会随着电流和温度的变化而变化,并不是一个恒值,波长的改变会引起莫尔条纹宽度的变化,继而影响到最终的测量结果。
2)光栅误差。光栅误差主要来自材料和制作工艺。制造光栅的材料要求在光栅刻划和后期使用过程中不变形,同时光栅基底的平面度和镀膜的均匀性应得到保证,且表面没有断痕、污点或其他缺陷,以确保莫尔条纹信号的质量。光栅的刻划误差可分为累积刻划误差和单刻槽刻划误差,其中累积误差是随着测量位移的加大而线性累积,这是对测量结果影响较大的误差源。
3)电路误差。由机械光栅式测缝计的结构可知,电路误差主要包括光电转换误差和电信号后处理误差。在光电转换器中,通过优化探测器的结构以及合理布置探测器的位置能够有效改善光电转换误差。电信号的后处理主要包括计数和细分两个部分,计数误差主要由过零点波动引起,提高光栅栅面质量能够有效减小该误差;另外光电转换输出电信号的质量、模数转换的精度以及不同的细分方法等均是引起细分误差的主要因素。
4)环境误差。在一定程度上,外界环境的振动、温度的变化和空气的扰动等因素会对测量结果产生影响。鉴于我国铁路线纵向跨度大,不同地区、不同季节的温差很大,下文着重分析温度变化对测量结果的影响。根据热胀冷缩的原理,温度的变化必然会使得光栅膨胀或收缩,进而导致光栅的累积误差发生变化,影响最终的测量精度。温度变化带来光栅累积误差的变化量可表示为:
(5)
式中:α为光栅材料的膨胀系数;Δl为温度变化引起的误差;L为光栅常量;T为客观环境温度;T0为光栅刻划时的温度。
一般情况下,玻璃光栅的膨胀系数为7.8×10-6m·℃-1,鉴于我国的四季温差较大,温度变化量可取30 ℃,光栅常量L取值50 mm,由此计算可得:
Δl=7.8×10-6×30×0.05=0.011 7 mm.
由此可见,温度变化对机械光栅式测缝计的影响可以不考虑。
3 精度分析3.1 测缝计的精度估算
结合上节中的误差分析,光栅误差和外界环境误差(主要是温度变化引起的误差)视为系统误差,分别用ΔS1和ΔS2表示;而光源误差与电路误差为随机误差,分别用ΔS3和ΔS4表示。则机械光栅式测缝计的误差ΔS可表示为[15]:
(6)
结合文献[14],光栅误差ΔS1可取0.41 μm,光源误差ΔS3可取0.032 μm,电路误差ΔS4取值为0.003 μm,环境误差ΔS2应取0.011 7 mm,将以上各值代入式(6),计算可得:
ΔS=0.012 2 mm.
上述结果是在理想条件下计算的机械光栅式测缝计精度的理论值,满足轨道板上拱监测亚毫米精度的要求;但在实际应用中,该理想条件难以达到,而且各项误差因素间的关系也更为错综复杂,为得到更具说服力的精度结果,需作进一步的精度检测实验。
3.2 测缝计的精度检测实验
为完成精度检测实验搭建室内测试平台,采用仪器有BD-CF00型机械光栅式测缝计、数显游标卡尺和位移标定支架,室内测试平台的具体结构如图5所示。

图5 精度检测平台示意图
检测方法为:首先利用位移标定支架模拟0~50 mm范围内的位移变形,位移变动分25次进行,相邻两次的位移变化值控制约为2 mm;同时采用机械光栅式测缝计和游标卡尺对位移进行测量,一共采集25个样本点;之后对比分析机械光栅式测缝计与游标卡尺的位移测量结果。测试结果见表1。

表1机械光栅式测缝计精度检测数据 mm
由表1可知,机械光栅式测缝计和游标卡尺具有高度相似的测量结果,其位移测量差异在0~0.3 mm范围内;机械光栅式测缝计的测量精度在亚毫米级,能够满足高精度的无砟轨道板受热上拱变形监测的需要。
4 测试实验
为进一步检验测缝计在无砟轨道板受热上拱监测中的有效性、可靠性和精度,在试验场搭建测试平台,并模拟无砟轨道板在铁路运营间的观测环境,完成传感器的仿真测试工作。测试平台在室外钢筋混凝土基础上搭建,提供市电电源(220 V,50 Hz),室外测试平台示意图如图6所示。
底座基础和轨道板大致水平,在后续的抬升和振动作用过程中能保持基础稳定和搭建结构的安全。A,B两点为千斤顶支撑点,用以模拟实现轨道板的上拱。C,D两点为机械光栅式测缝计安装位置,用以模拟无砟轨道板端头上拱处的监测点位。机械光栅式测缝计基座和顶针贴片采用粘合方式安装,之后用简易安装装置(U型卡壳)固定传感器,这便于传感器的安装和拆卸。同时在C′,D′两点处安装测量精度为0.01 mm的机械百分表。实际测缝计的位移监测量和机械百分表的位移监测量有所不同,因此在进行数据对比分析前需要将百分表的观测值按三角函数关系归化至C,D位置的读数。传感器及百分表的安装效果如图7所示。
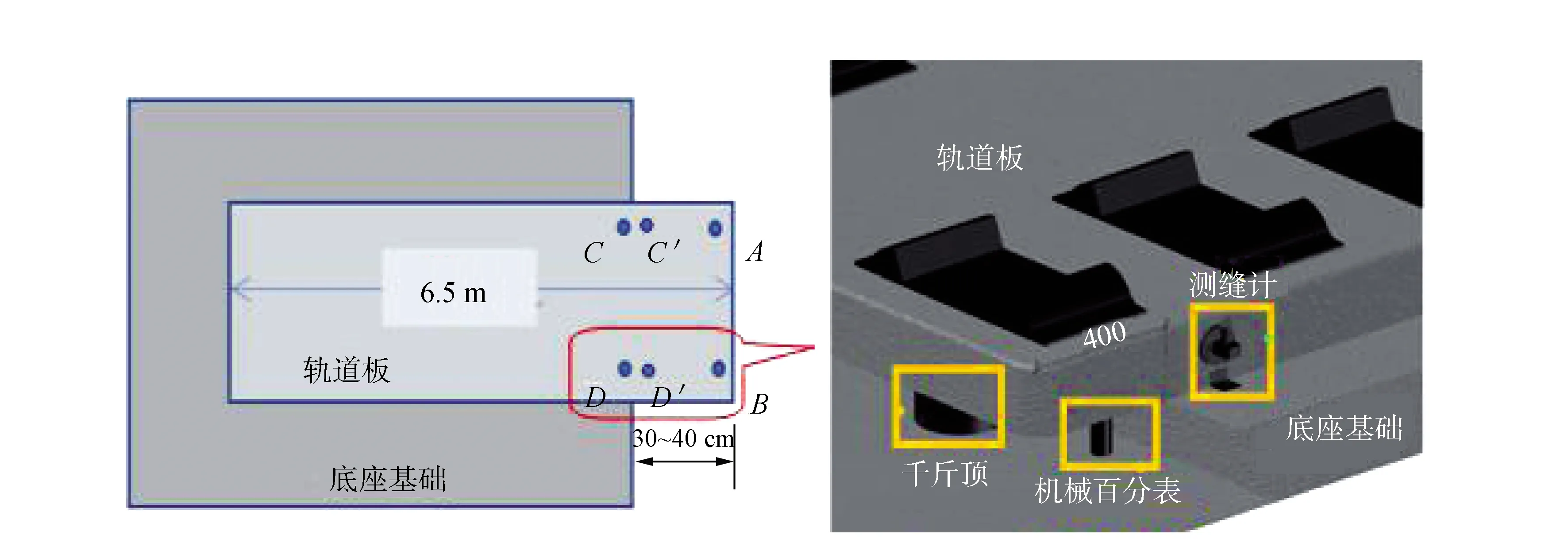
图6 室外测试平台示意图

图7 传感器及百分表安装效果示意图
室外实验平台搭建完成后,模拟无砟轨道板在铁路运营期间的观测环境,分别为常温、高温、振动和淋水等环境条件,并据此拟定4种测试方案,分别在夯机、取暖器和淋水装置等设备的辅助下完成传感器的测试工作;测试过程中机械光栅式测缝计的数据采样频次设定为“10 s/次”,由读数设备自动采集;机械百分表的数据大约每5 min读取一次,由人工进行读数并记录。
方案一:常温条件,温度约为24 ℃;测缝计和百分表安装完成后,实验平台先静置15 min,其后约每间隔10 min两侧千斤顶进行一次同步顶升作业,记录实验结果。
方案二:高温条件,使用取暖器对C,D两点处的测缝计进行加热使局部温度达到50~60 ℃,同时分4次降低千斤顶的高度,记录实验数据。
方案三:振动条件,使用夯机轮流对上部轨道板、下部底座基础施加振动效应,局部振动强度达到110 dB,同时调整千斤顶的高度,记录实验结果。
方案四:加湿条件,使用淋水装置轮流对C,D两点的测缝计进行淋水,淋水强度约为10 cm/h,期间分4次调整千斤顶的高度并记录实验数据。
具体实验结果如图8—图11所示。
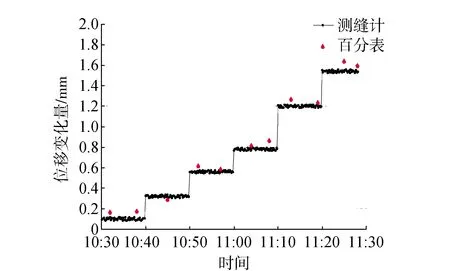
图8 常温条件下传感器的测试结果
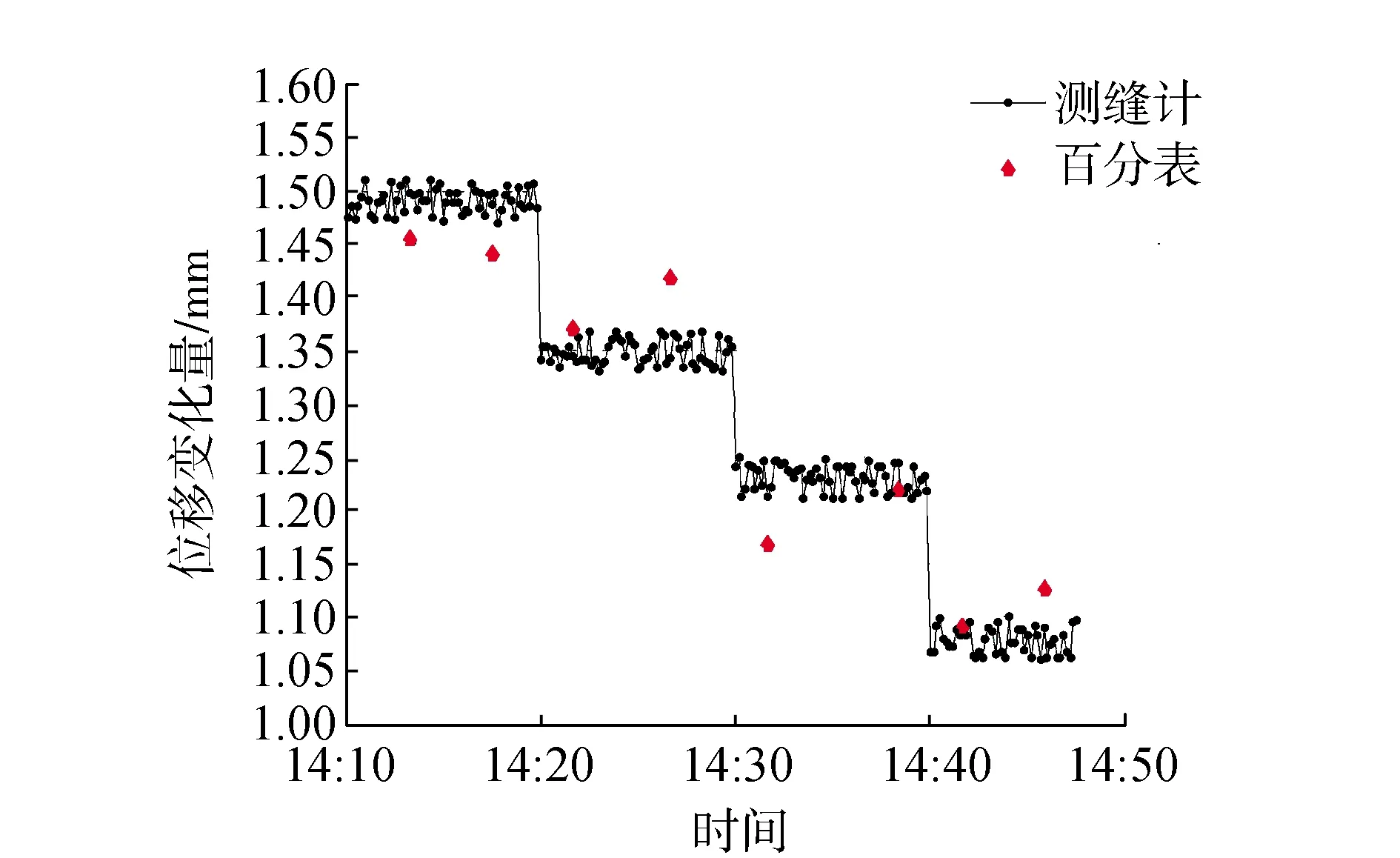
图9 高温条件下传感器的测试结果

图10 施加振动影响下传感器的测试结果

图11 加湿条件下传感器的测试结果
综合以上各方案的实验结果见表2,其中精度指标是以各阶段(以千斤顶的高度调整划分)百分表的监测结果为基准值求算得测缝计观测值的中误差,若同一阶段有多个百分表记录值,则取平均值作为基准值。
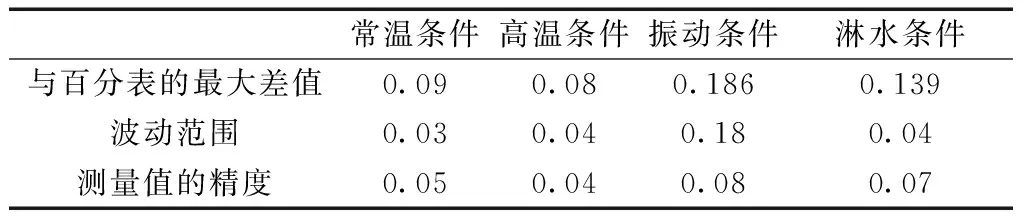
表2 机械光栅式测缝计的测试结果 mm
由表2可知,测缝计与百分表的测量值最大权差小于0.2 mm,且以百分表的监测结果为基准值计算传感器监测结果的精度均小于0.1 mm,可见测缝计和百分表在模拟轨道板上拱监测中具有高度相似的测量结果。此外,在常温、高温和淋水条件下测缝计的观测数据噪声波动维持在0.05 mm的水平,机械光栅式测缝计的温漂不明显,具有防水功能。在振动条件下观测数据的噪声波动达到0.18 mm,但数据序列整体仍趋于稳定,振动时无大的阶跃现象发生;考虑到千斤顶在振动时其液压系统可能下降,以及轨道板在振动过程的竖向弹性形变,这一监测结果能够说明传感器具有亚毫米级的测量精度,能够抵抗高温、高湿和振动的不良影响,这十分有利于传感器对小量程的位移变形进行监测。
5 结 论
在分析机械光栅式测缝计测量原理、误差源和测量精度的基础上,通过搭建实验平台,模拟机械光栅式测缝计监测轨道板上拱的客观环境条件,完成传感器的仿真测试工作。实验结果表明,机械光栅式测缝计在振动、高温和淋水等条件下的观测数据稳定,能够抵抗高温、高湿和振动等不良条件的影响,监测结果的精度达到亚毫米级,满足轨道板上拱监测的精度要求。
