三原则整体最小二乘用于平面自由网平差计算

郭绍禹

(江西理工大学，江西 赣州 341000)

“整体最小二乘理论”应用到测绘领域是一种新理论，是近十年来许多学者的研究方向，并取得了算法和应用方面的研究成果[1-12]。但是，还缺少适用于平面自由网平差的研究成果。

由Adcock[13]提出的“系数矩阵A有误差ΔA”需添加改正数VA的整体最小二乘模型可写为：

(1)

(2)

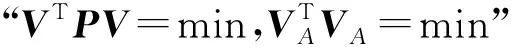
文中在“平面网平差”中应用了“整体最小二乘理念”，获得一种“三原则整体最小二乘”新方法，它能消除“系数误差ΔA和参数系统误差Δx”，适用于平面自由网平差。

1 最小二乘的模型和误差

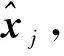
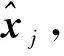
(3)

(4)

(5)

(6)

Δxj=xj-d=QjATPAd-d.

(7)

当XO的误差ΔX=XO-XⅡ≈XⅠ-XⅡ=-d的绝对值小于0.3 m(作者实验值)时，误差ΔA对V没有影响。

当误差ΔX大时，用XO计算的系数矩阵A有误差ΔA，其非线性误差会影响平差而使V增加新误差ΔV。为了去掉ΔV，应该消除系数误差ΔA。

2 三原则整体最小二乘的模型

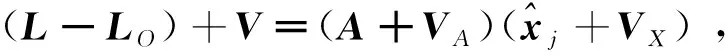
(8)

(9)

的三原则整体最小二乘即TPTLS新方法。

为了保持式(9)中各量的相同数量级，文中设定检验V，VA，VX末位数值的单位是：V单位(″)；在VA=VA×107之后VA=1；VX单位mm。

算例实验容易实现VA，VX的绝对值小于0.01，明确规定0.5是检验数值标准。当由电脑检验VA，VX的Abs(V)<0.5时，则显示VA=0，VX=0(注意这里的0不是数学0，而是显示为0)，则分别消除了原先的误差ΔA，Δxj。

由此观念和经验认识：TPTLS模型是“经过很多次的平差”，还要“多次的由电脑检验VA=0，VX=0”的模型式。

3 三原则整体最小二乘的解算方法

TPTLS解算方法不是唯一的，文中介绍两种方法。

第一种TPTLS解算方法：灵活采用LS解算法，很多次循环运行LS，多次换用“参考点组”或“近似坐标”，逐次改变A等各种值趋近最终值，最后实现“VA=0，VX=0”而满足三原则的准则。

逆阵Qj的计算式为：

(10)

(11)

协因数Qxx的计算式为：

Qxx=Qj(ATPA)Qj.

(12)

当平差运行到第2)大平差步骤时才需要计算改正数VA，VX，其计算式：

VA=Ai-Ai-1,

(13)

(14)

第i次运行VA，VX的检验过程如下：

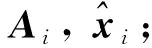
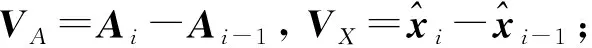
4)检验绝对值：VA=VA×107， Abs(VA)<0.5,Abs(VX)<0.5 mm(在数组中分别保存VA，VX值供最后输出用) 。

当检验绝对值均小于0.5时，即显示VA，VX为0，结束循环运行；否则继续。

稳定性检验用文献[17]的单点检验，判别式为：

(15)

在文中，系数误差是“系数矩阵A的误差”的简称。因为是灵活采用LS解算法，因此不需要组成“系数矩阵误差”。

4 TPTLS的平差步骤

TPTLS自由网平差的要求：

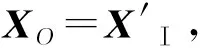
2)要消除→误差ΔA，系统误差Δxj，粗差值L；

3)要“各个参考系”都得出相同的“各种平差值”。

TPTLS自由网平差的两大平差步骤为：

1)多次换用“参考点组”，选出w个稳定点：LS自由网平差多次循环运行；多次换用“参考点组”，利用式(10)—式(12)、式(15)求解；每次单点稳定性检验去掉一个参考点，最后选出w个稳定点的w号点组，结束循环。

2)多次换用“近似坐标”，消除误差ΔA，Δxj：LS自由网平差多次循环运行；多次换用“新近似坐标”，w号点组不变，利用式(10)—式(14)求解；每次检验是否Abs(VX)<0.5 mm，当满足此式时结束循环。然后运行“粗差检验”；最后按指定的参考点组利用式(10)～式(12)、式(15)求解一次后输出成果。

5 模拟算例

模拟算例的数据来源：假设Ⅰ，Ⅱ期的真坐标XⅠ，XⅡ，计算真位移d=(XⅡ-XⅠ)，d作为Ⅱ期检验系统误差的依据；反算出真观测值LⅠ，LⅡ，添加随机误差得出观测值LⅠ，LⅡ。

模拟算例说明(用Basic 6.0 企业版编制的通用程序)：

1)权P=1未打印，成果是最后一次的，进行粗差检验；

2)新Xo是最后的Xo；VA是VA；Vx是VX；Δx是Δxj；

3)VX全部输出；VA因太多而只输出两个方程的VA值。

5.1 证明TPTLS消除误差ΔA，Δxj

理论上证明“误差ΔA， 系统误差Δxj”是否消除的最好方法是：采用真坐标X，真观测值L，近似坐标XO，分别运行各种平差方法：

2)运行TPTLS，得改正数V=0，平差值L′=L，平差坐标X′=X，则证明误差ΔA，Δxj已消除。

因真观测值无误差，应该是V=0 ，X′=X。

表1是用真观测值的TPTLS自由网平差算例：真观测值L，S是与真坐标X配套的，近似坐标XO是前期的，平差能得出改正数V=0、平差坐标X′=X，这是从理论上严密证明：TPTLS消除了误差ΔA，Δxj。

表1 用真观测值三原则整体最小二乘平面自由网平差

表2是用真观测值的LS自由网平差算例：原始数据同于表1，平差得出V≠0、平差坐标X′≠X，这是从理论上证明：LS结果含有误差ΔA，Δxj影响。该算例是用来对比表1，证明TPTLS消除了误差ΔA，Δxj。

表1可看出：平差值L′=真观测值L；V=0；VA=0；稳定点的位移x=0；X′=X；Vx=0；Δx=0。

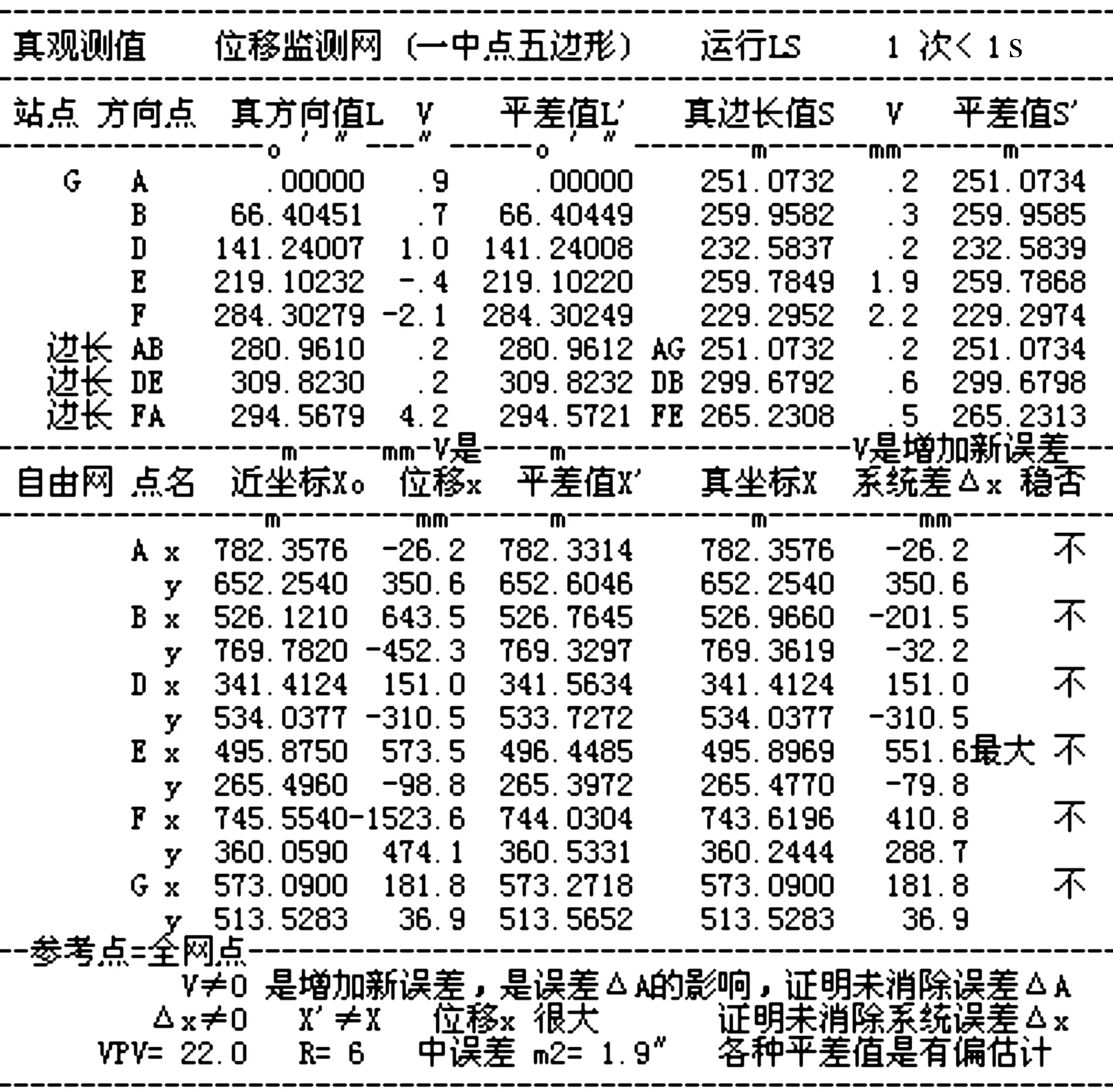
表2 用真观测值最小二乘平面自由网平差

表2可看出：L′≠L，V是增加新误差，证明有ΔA影响；稳定点位移x≠0；X′≠X；Δx≠0，证明有Δxj影响。

5.2 TPTLS的各个参考系均得出相同结果

表3、表4是用观测值的TPTLS自由网平差算例：原始数据相同，参考系不同，即表3的参考点组(ABDEFG )与表4的(ADF)不同，平差均能得出“各种平差值”完全相同，这也证明：TPTLS消除了误差ΔA，Δxj。

表3 三原则整体最小二乘平面自由网平差(ABDEFG)

表4 三原则整体最小二乘平面自由网平差(ADF)

表3、表4可看出：V，X′,位移x等“各种平差值”完全相同。

含有位移点的不同点组共有(26-23)=56组，定义56个不同参考系，采用TPTLS均能得出相同的“各种平差值”结果，即与参考系的选择无关。

表5为表1—表4的平差方法结果对比。采用LS则得出不同的结果；采用满足式(2)的TLS则得出V相同、位移x不同的结果。

表5 平差方法结果对比

6 结束语

2)TPTLS解算方法不是唯一的。文中采用LS解算法：先多次换用参考点组，后换用近似坐标，用LS的很多次平差运行来满足三原则的准则式(9)。这种解算方法能够消除“系数误差ΔA和参数系统误差Δxj”，各个参考系均能得出相同的“各种平差值”，且符合实际的无偏估计。

3)TPTLS方法适用于平面自由网平差，其最大的优点是：Ⅱ期选用“各个参考系”均能得出相同的“各种平差值”(即与参考系的选择无关)，且能得出真位移d的无偏估计的位移x。经典的LS方法存在有“多个参考系得出多套位移x”的系统误差问题，TPTLS方法有效解决了此类问题。