回归分析中内外符合精度指标研究

王仲锋

(长春工程学院 勘查与测绘工程学院，长春 130021)

本研究将导出用检验数据的模型残差计算单位权方差的无偏估计公式，并将其计算的单位权方差的无偏估值与建模时获得的单位权方差无偏估值分别作为模型的外、内符合精度指标值。

1 内符合精度公式

设以L为观测值的线性回归的高斯-马尔柯夫模型为：

(1)

(2)

现将L分为n1×1和n2×1的两组向量L1和L2(对应的权矩阵分别为P1和P2，协因数阵分别为Q1和Q2，互协因数阵Q12=0，且Pi和Qi互为逆阵)，第一组用作建模，第二组用于外符合检验。相应地式(1)亦可分为两组。

(3)

(4)

可见，对式(3)、式(4)两边求数学期望有：

(5)

(6)

将式(3)写成误差方程形式，即有：

(7)

(8)

对式(8)两边求数学期望，顾及式(5)可得：

(9)

顾及式(5)和(9)，可得：

(10)

另外由：

(11)

和协因数传播率，可得：

(12)

考虑到P1和Q1互为逆阵，整理式(12)得：

(13)

其中，E1为n1×n1的单位矩阵。

(14)

其中r1称为多余观测数，且：

r1=n1-t.

(14a)

文献[17]是根据概括平差模型导出单位权方差估计公式的，为了使读者更加清晰地理解式(14)，以下按照论文的体系对式(14a)进行详细推导。

(15)

去掉期望值符号即可得到式(14)。其中，Et为t×t的单位矩阵，t为参数的个数。

2 外符合精度公式

(16)

记基于L2(外符合检验数据)的回归模型残差向量为e2，即：

(17)

根据协因数传播率，可得e2的协因数矩阵：

(18)

考虑到Q1和P1互为逆阵以及转置矩阵的性质，整理后有：

(19)

对照式(13)和式(19)，式QV1V1和Qe2e2差异显著，原因在于L1参加了建模平差计算，L2未参加平差计算。

(20)

同样，考虑到式(6)和式(9)，对式(17)两端求数学期望得：

(21)

可见，式(20)又可写为：

(22)

将式(19)带入式(22)，同样考虑到P2和Q2互为逆阵以及矩阵迹的性质tr(AB)=tr(BA)得：

(23)

记：

(24)

(25)

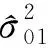
需要说明的是，像坐标转换、大地水准面拟合一类的问题，观测值均视为等精度的独立观测值，上述有关公式中的权阵均取单位阵。

3 与经典公式的比较

根据经典方法，内符合精度的公式可以写作：

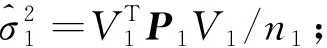
(26)

外符合精度的公式可以写作：

(27)

根据以上讨论，并考虑到r1n2，可将式(14)与式(26)、式(25)与式(27)进行比较，结果列入表1。

由表1及误差理论等相关知识可做如下分析：

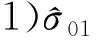
表1 与经典公式的比较

4 实例分析

香港特别行政区共74个GNSS/水准控制点，其HK80和WGS84空间直角坐标见表2，点位分布见图1。取表2中60-74号点作为建模点(如图1中“口”形符号所示，共计15个)，1-59号点作为检验点(如图1中“◇”形符号所示，共计59个)，现利用布尔沙模型进行HK80至WGS84的坐标转换。

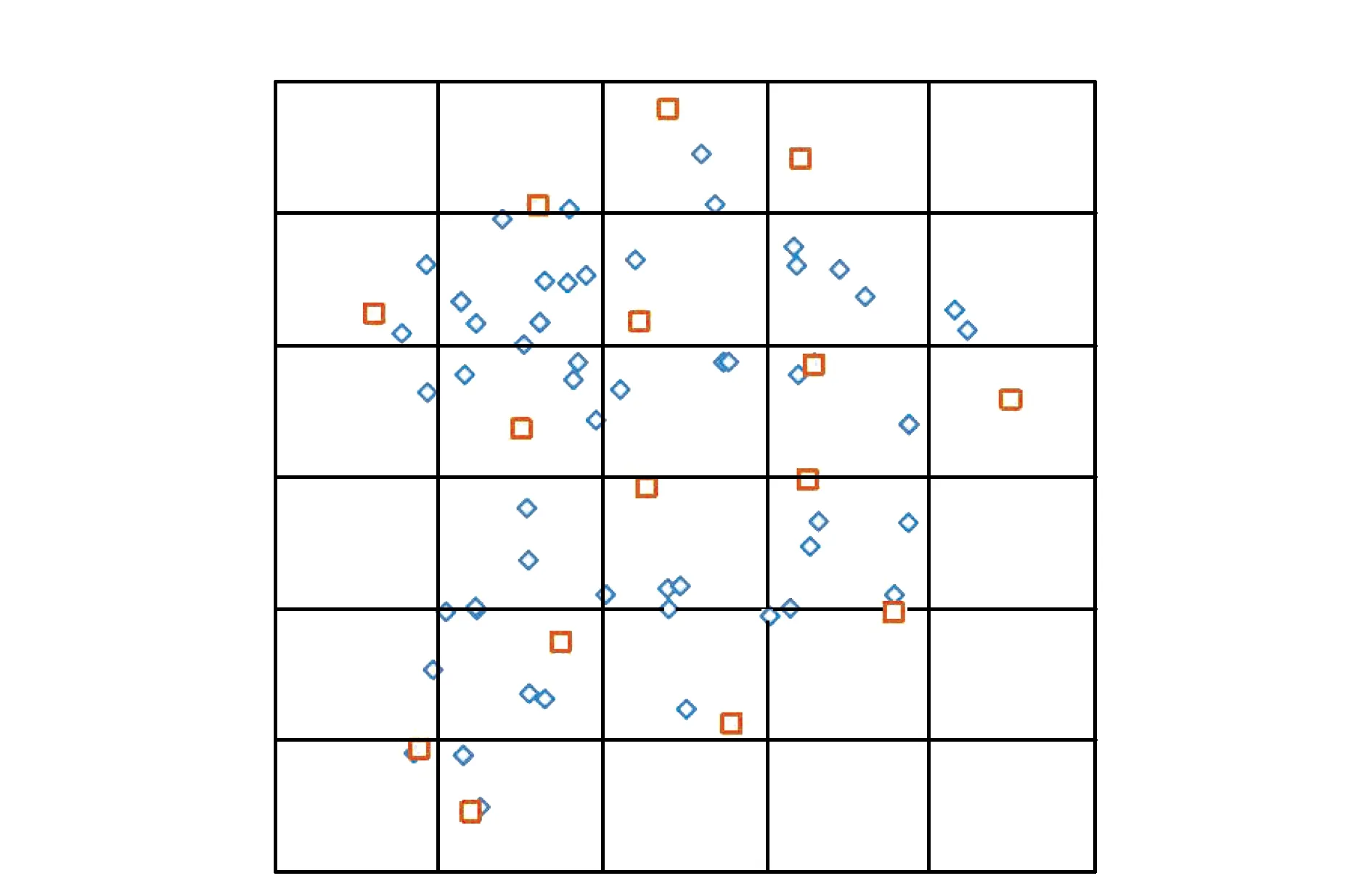
图1 香港GNSS/水准点点位分布图

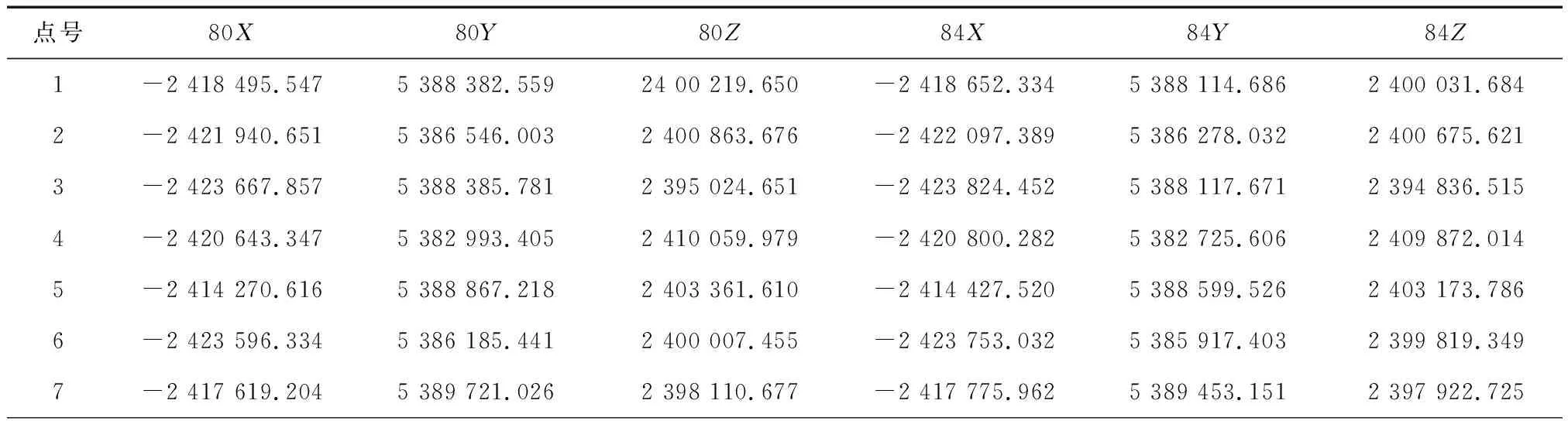
表2 HK80及WGS84空间直角坐标(椭球上的投影点坐标)

续表2

续表2

可按照下列方式列立第i点的误差方程。

(28)

其中，

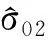
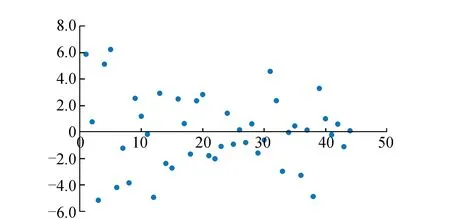
图2 建模数据在XYZ 3个方向的离差分布图

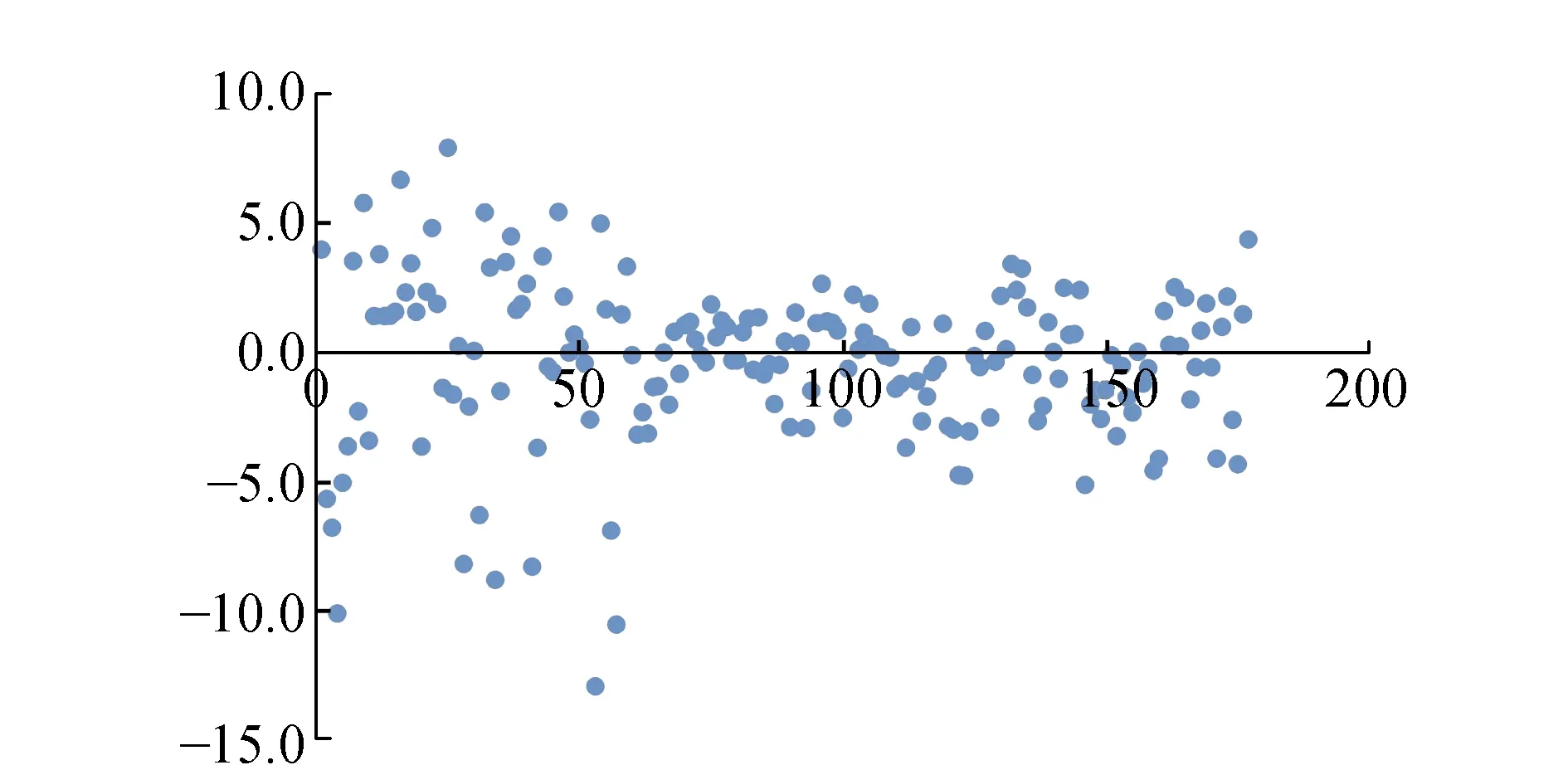
图3 检验数据在XYZ 3个方向的离差分布图

表3 内外符合精度计算结果表

4 结 论