融合粒子群的缎蓝园丁鸟优化算法及应用

2022-01-26李宁高鹰翁金塔曹灿郭晓语周灿基

现代计算机 2021年34期

李宁，高鹰，翁金塔，曹灿，郭晓语，周灿基

（1.广州大学计算机科学与网络工程学院，广州 510000；2.中国科学院信息工程研究所，北京 100000）

0 引言

群体智能算法［1］是受到自然界生物启发，通过生物的生活方式和生活特性模拟设计的一种算法，可以解决经济、社会和自然科学等领域中各种复杂的优化问题。常见的有粒子群优化（par⁃ticle swarm optimization，PSO）算法［2-3］，通过模拟鸟群的捕食行为来寻找最优解；人工鱼群算法（artificial fish swarm algorithm，AFSA）［4-5］是通过模仿鱼类在水中的活动方式，总结出鱼群的随机、觅食、聚群、追尾等四种典型的行为来实现寻优；近年来也有许多新的群智能算法被提出，如象群优化（elephant herding optimization，EHO）算法［6-7］源于自然界中大象的畜牧行为，可以用于解决全局无约束优化问题。群智能算法具有简单性、可扩展性和运行时间短等特点，在解决各种寻优问题时，具有良好的操作性和强大的表现力。

缎蓝园丁鸟优化（satinbower bird optimization，SBO）算法［8］是Moosavi和Vahid Khatibi Bardsiri于2017年模拟自然界成年雄性缎蓝园丁鸟的求偶行为而提出的一种新型群智能算法，并与自适应神经模糊推理系统（adaptive network-based fuzzy in⁃ference system，ANFIS）组合，有效地提高了软件开发工作评估的准确性。目前国内对于该算法的改进主要有基于自适应t分布变异的缎蓝园丁鸟优化（satin bower bird optimization based on adaptive t-distribution mutation，tSBO）算法［9］和自适应权重缎蓝园丁鸟优化（satin bower bird optimization based on adaptive weight，WSBO）算法［10］。t SBO引入了自适应t分布变异算子，使用算法的迭代次数作为t分布的自由度参数来增强种群的多样性，避免原算法陷入局部最优；WSBO通过自适应权重的方法和改进原算法中高斯布函数来提高原算法的搜索能力。这两种改进都在一定程度上提高了SBO算法的性能，但是这些改进算法在求解精度和收敛速度上仍有很大的缺陷。

为了进一步提高SBO算法的收敛精度，搜索能力和收敛速度，本文提出了一种基于PSO算法改进的SBO（particle satin bower bird optimization，PSBO）算法。PSBO算法中引入了速度因子来增加算法的搜索速度和搜索能力；采用固定的惯性权重因子来提高算法的收敛性以及避免算法陷入局部最优。通过求解8个典型复杂函数的最优解来验证PSBO算法的寻优能力，并将其应用到支持向量机（support vector machines，SVM）内部参数优化的问题中，验证其有效性，拓宽了应用范围。

1 缎蓝园丁鸟优化算法

在自然界中，成熟的缎蓝园丁雄鸟在其各自的领地上建造求偶亭，并配以各种装饰来吸引雌鸟，然而并不是所有的成年雄鸟都能成功的构建和维护求偶亭，存在求偶亭被破坏的情况［11］。根据缎蓝园丁鸟求偶的原理，在自然界中，成熟的缎蓝园丁雄鸟在其各自的领地上建造求偶亭，并配以各种装饰来吸引雌鸟，然而并不是所有的成年雄鸟都能成功的构建和维护求偶亭，存在求偶亭被破坏的情况［12］。根据缎蓝园丁鸟求偶的原理，可以将SBO算法分为以下五个步骤：

（1）初始化种群。在可行域内随机生成一个包含N个求偶亭的初始种群，每个求偶亭的位置定义为D维，当前迭代次数为t，最大迭代次数为Max It。

（2）计算每个求偶亭的吸引力。每个求偶亭的吸引力P i由公式（1）或得，fiti通过公式（2）计算：

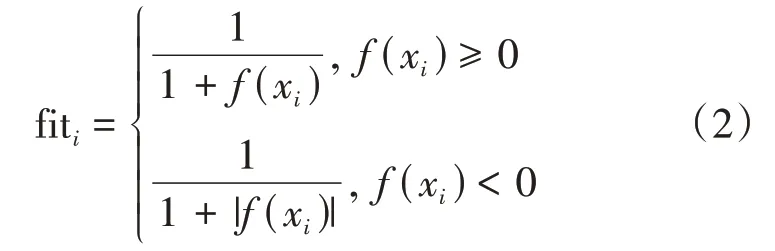
式中：fiti表示i个求偶亭的适应度值，f(xi)是第i个求偶亭的目标函数，每次迭代保证目标函数的函数值不断减小。

（3）更新种群位置。雄性园丁鸟根据历史经验并利用信息共享机制，不断调整求偶亭的位置，其位置更新公式如式（3）所示：

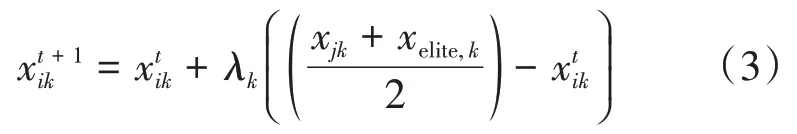
式中：为第t代第i个个体的第k维分量;x j通过轮盘赌选择机制确定；xelite,k为整个种群当前的最优位置的第k维分量；λk是步长因子，通过式（4）计算：

式中：α为最大步长，P j是目标求偶亭被选中的概率，概率值在0到1之间，步长与目标位置的概率成反比，目标位置的被选中概率越大时，步长越小。

（4）个体变异。根据缎蓝园丁雄鸟的求偶习惯，强壮的雄鸟会从较弱的雄鸟那里偷取材料，甚至破坏其求偶亭。因此算法以一定的概率随机变异，在这个过程中，xi k服从正态分布，如公式（5）所示：

在（6）式中，δ为标准差，通过公式（7）计算：

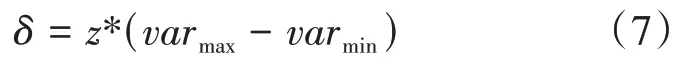
式中：z是缩放比例因子，varmax和varmin分别是变量xi的上限和下限。

（5）组合种群。在每次循环的最后，对旧种群和从变异获得的群体进行组合，形成组合种群，并对组合种群中的所有个体的代价函数值从小到大进行排序，保留函数值最小的个体，淘汰其他个体。若此时满足终止条件，则输出最佳位置及其对应的最优值，否则继续进行迭代。

2 基于粒子群改进的缎蓝园丁优化算法

2.1 粒子群优化算法

PSO算法是一种模仿鸟类捕食的群体智能的随机全局优化算法，其参数简单易于实现，收敛速度快且全局搜索能力较强［13］。在PSO算法中，设计了一种无质量的粒子来模拟鸟群中的鸟，每个粒子可视为D维搜索空间中的一个搜索个体，并且具有速度和位置两个属性。粒子的当前位置即为对应优化问题的一个候选解，粒子的飞行速度可根据粒子历史最优位置和种群历史最优位置进行动态调整，通过群体中粒子之间的协作和信息共享来寻找最优解。

假设PSO算法中粒子的数量为pop，在t次迭代中，对于粒子i=1,2,3,…,pop，在D维搜索空间中，每个粒子i的速度用vi=(vi1,vi2,vi3,…,vin)t表示，位置用xi=(xi1,xi2,xi3,…,xin)n表示，则第i个粒子的速度用用公式（8）进行计算，位置用公式（9）进行计算：

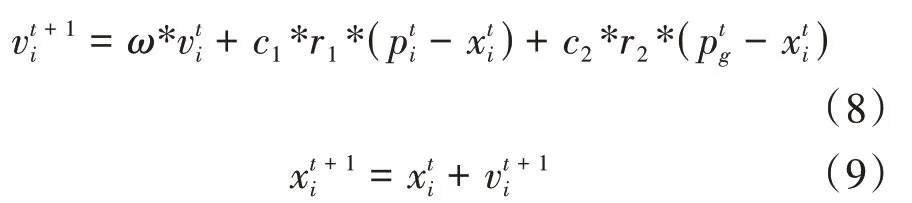
式中：vti是粒子第t次迭代的速度，xti是粒子第t次迭代的当前位置，pti是粒子i搜索到的历史最优位置，ptg是粒子搜索到的全局最优位置；c1和c2都是加速常数；r1,r2∈[ 0,1]，ω是惯性权重系数。

2.2 改进的缎蓝园丁鸟优化算法

在基本的SBO算法中，种群位置的更新依赖于轮盘赌选择机制和整个种群当前的最优位置，这样种群的随机性很小，缎蓝园丁鸟个体的位置更新容易受到适应度较好的位置的影响，导致算法的搜索能力很差，本文引入了粒子群算法中的速度因子，来增加算法的搜索能力，使每个种群朝着更好的方向更新，提高算法的收敛精度和收敛速度。具体的更新策略为：在每次迭代时，将种群中每只雄性缎蓝园丁鸟的求偶亭视为粒子群中的每个粒子，给每个粒子一个速度因子，如公式（10）：

式中：是粒子第t次迭代的速度，为第t代第i个个体的第k维分量，x j通过轮盘赌选择机制确定，xelite,k为整个种群当前的最优位置的第k维分量；c1和c2为学习因子；r为常数；ω是惯性权重系数；则改进的位置更新操作为：

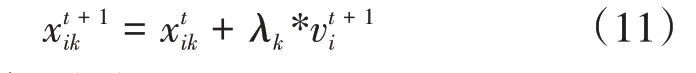
式中：λk是步长因子。

速度因子引入改进的缎蓝园丁鸟优化算法在搜索能力和速度上都有一定的提高，但是收敛精度不够理想，基于PSO算法速度因子中引入惯性权重的启发，本文给种群中每只雄性缎蓝园丁鸟的求偶亭一个速度因子中的固定惯性权重，来提高种群的多样性。结合速度因子的引入，最终改进算法的位置更新操作如公式（12）。

3 PSBO算法性能分析

3.1 测试函数以及参数设置

为了验证PSBO算法的有效性，本文对8个基准测试函数进行仿真实验来检验算法的改进效果，选取的测试函数中包含单峰、多峰等不同特征的测试函数，其中f1～f5为单峰函数，f6～f8为峰函数，如表1所示。

表1 测试函数

续表1

为了更进一步验证PSBO算法在收敛速度和收敛精度上的优越性，本文将其与SBO算法、WSBO算法、t SBO算法和PSO算法进行比较，实验环境为Window 10操作系统，算法用Matlab R2021a编写。实验的最大迭代次数为500，xmax和xmin分别为每个测试函数定义域的上限和下限，种群数为20，维度为30，各算法其余的参数设置如表2所示。

表2 算法参数设置

3.2 实验结果及其分析

为减少实验中随机性的影响，在对每个测试函数独立运行30次，计算其最优值、均值和标准差，实验结果如表3所示。对于每个测试函数，在固定迭代次数下，最优值反映了算法的寻优能力和收敛精度，均值和标准差反映了算法的鲁棒性和稳定性。

表3 五种算法实验结果

从表3的数据可以看出，对于所有测试函数，本文提出的PSBO算法的最优值、平均值和标准差均明显优于SBO、WSBO、tSBO和PSO。对于函数f1、f4、f6和f7这四个函数，PSBO算法都能找到其理论最优值，且其中f1、f6和f7的标准差都是0；对于其他的测试函数，PSBO算法的性能在很大也程度上优于其他算法。

为了能更直观地显示PSBO算法的优化效果，图1到图8给出了5种算法在8个标准测试函数f1～f8上搜索函数最优值过程中随迭代次数增加的收敛曲线。从图中可以看出，不管是多峰函数还是单峰函数，PSBO算法的收敛精度和收敛速度都是最好的。

图1 f 1函数收敛曲线

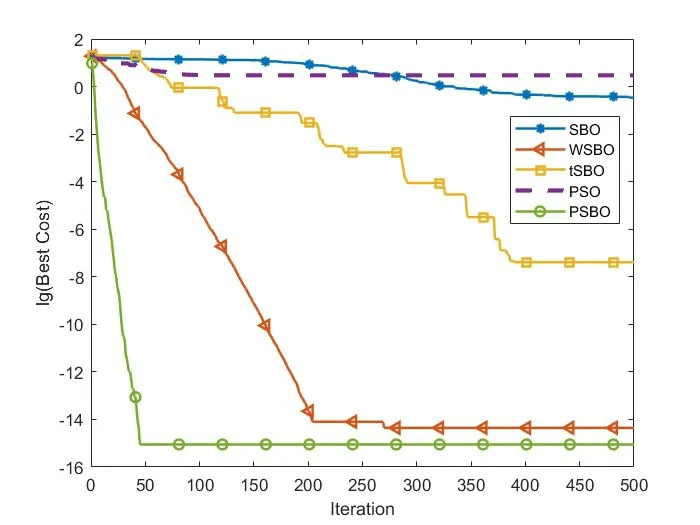
图8 f 8函数收敛曲线

从图中可以看出，除了测试函数f8，PSBO算法寻优过程的变化近似于直线，这充分表明，PSBO算法的寻优速度更高，收敛速度更快，全局搜索能力更强；其中，从f6和f7这2个函数收敛曲线可以看出，虽然WSBO算法和tSBO算法也能找到理论最优值，但是它们的收敛速度远不如PSBO算法，在迭代次数不到50时，PSBO算法已经找到了理论最优值；从f8的函数收敛曲线可以看出，虽然PSBO最终找到的最优值并不是很理想，但是对比其它算法已经有了很大提升，特别是在收敛速度上，在迭代次数不到50时就已经找到了比其它算法都要精确的值；从f1、f2、f3、f4和f5的函数收敛曲线可以看出，在迭代过程中，PSBO算法能够快速接近于理论最优值。

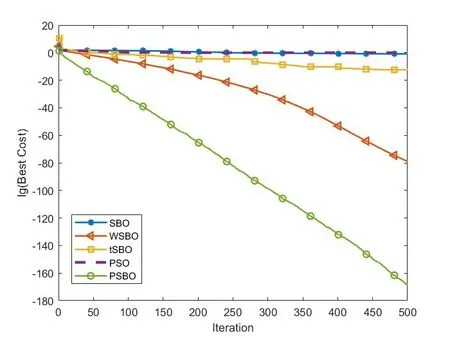
图2 f 2函数收敛曲线

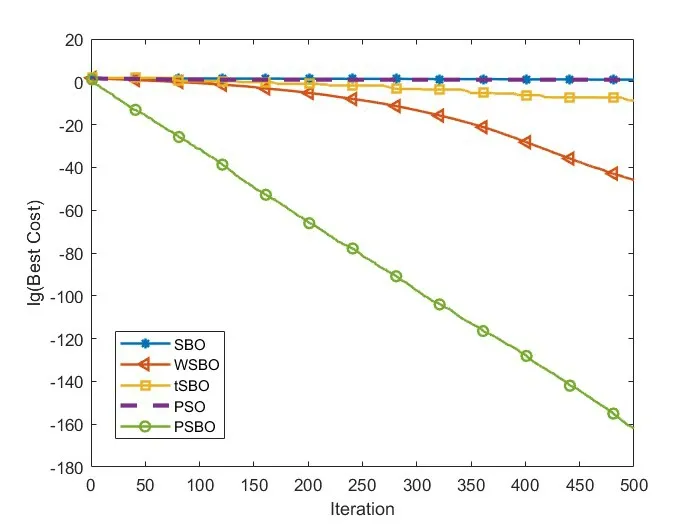
图3 f 3函数收敛曲线

图4 f 4函数收敛曲线

图5 f 5函数收敛曲线

图6 f 6函数收敛曲线

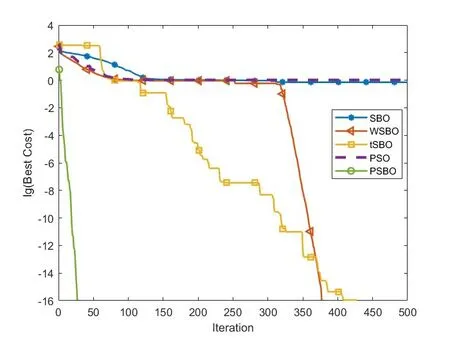
图7 f 7函数收敛曲线

4 基于PSBO算法的SVM参数优化

在以往的SBO算法应用中，如2017年Moosavi等人提出了SBO算法并将其与ANFIS结合，用来提高软件开发工作评估的准确性；2018年，El-Hay等［14］用SBO算法来实现固体氧化物燃料电池的精确参数测量；Jagadeeswar等［15］将SBO用于电力系统的阻塞管理，计算最小的阻塞代价，采用基于发电量重调度的方法来缓解输电线路的阻塞等，还未有基于机器学习函数参数优化方面的相关应用。为此，本文提出了一种利用BSO及其改进算法PSBO来优化SVM参数的应用方向，并验证了PSBO的有效性和可行性。

4.1 SVM基本原理

SVM由Vapnik等［16］于1995年提出，是一类按监督学习方式对数据进行二元分类的广义线性分类器。SVM的基本思想是使用内核函数把输入样本空间映射到高维特征空间，在高维空间中求得一个最优分类面，支持向量则是指在间隔区边缘的训练样本点。

以二分类为例子，假设给定一个特征空间上的训练集数据T={(x1,y1),(x2,y2),(x3,y3),…,(xN,y N)}，其中，xi表示第i个特征向量，y i∈{1,-1}，y i为类标记，当它等于1时为正例，为-1时为负例,如果数据是线性可分的，则存在分类超平面ωx+b=0，能对所有样本进行正确的划分。为了使SVM的分类效果最佳，需要寻找最优超平面，可以将最优分类面的问题转化为如下的约束优化问题：

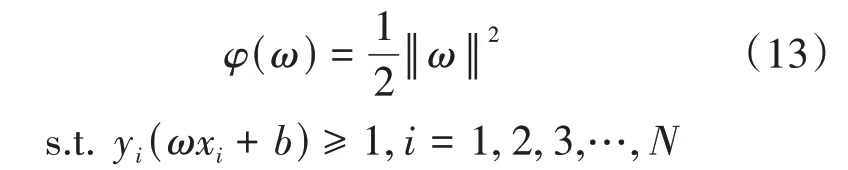
式中：ω是超平面的法向量，b是超平面的常数项。

当数据集线性不可分时，SVM利用内积核函数代替向高维空间的非线性映射，在低维空间上进行计算，在高维空间进行分类效果表征，减少了计算的复杂度。

参数优化是SVM研究中的一个重要问题，参数选择的不同会直接影响SVM模型的分类预测精度和泛化能力，影响SVM性能的主要参数就是核参数g和惩罚因子C。分类问题中，g越小，低维空间中选择的曲线越复杂，容易出现过拟合；g越大，分类的精确度越低，容易出现欠拟合；惩罚因子C越大，经验风险越小，结构风险越大，容易出现过拟合；C越小，模型复杂度越低，容易出现欠拟合［17］。因此需要选择更优的参数C和g，来提高SVM的分类性能。

4.2 PSBO算法优化SVM参数

本文将PSBO算法与支持向量机结合，用求偶亭位置的更新来寻找SVM中最优的核参数g和惩罚因子C，将wine数据集中第一类的1-30，第二类的60-95，第三类的131-153做为训练集，第一类的31-59，第二类的96-130，第三类的154-178做为测试集，利用K折交叉验证的方法算出验证结果准确率的均值作为目标函数，找出目标函数的最优值对应的核参数g和惩罚因子C，具体步骤如下所示：

（1）对wine数据集进行预处理，将将训练集和测试集归一化到［0，1］区间，并初始化PSBO的各项参数。

（2）初始化核参数g和惩罚因子C，将它们看做PSBO算法中的求偶亭，用训练集训练模型，对数据进行分类，计算出目标函数和全局最优的求偶亭位置。

（3）根据公式（1）和公式（2），计算每个求偶亭的吸引力。

（4）根据公式（12）来更新每个求偶亭的位置。

（5）随机变异，并判断求偶亭的位置是否溢出，如果位置溢出，对位置进行处理。

（6）再对数据进行分类，重新获得个体的适应度值。

（7）更新求偶亭的个体最优位置和群体最优位置。

（8）计算每一代的个体全局最优适应度值。

（9）判断迭代次数是否为最大迭代次数，若是，结束算法并输出核参数g和惩罚因子C的最优解和最优目标函数。

（10）用计算出的参数g和惩罚因子C构建分类模型，对测试数据进行分类预测并计算其准确率。

4.3 实验结果及其分析

在实验中，将SVM分别与PSBO算法、SBO算法和PSO算法结合，以验证本文改进的PSBO算法在SVM参数优化中的性能。其中，设置迭代次数为100，种群规模为20，其中惩罚因子C的最大值设定为1015，最小值为10-1，核参数g的最大值设定为103，最小值设定为10-4，则VarMax为1015，VarMin为为10-4，设置5次K折交叉验证，其他参数如表4所示。

表4 参数设置

为了防止实验的偶然性，对每个算法进行独立的30次试验，记录模型分类最高的准确率和最低的准确率和对应的核参数g和惩罚因子C的数值，以及测试集准确率，如表5所示。

表5 SVM参数优化结果

从实验结果可以看出，SBO算法并不适用于SVM参数的优化，没有办法对目标函数进行优化；而改进的PSBO算法和PSO算法都可以对核参数g和惩罚因子C进行较好的寻优，实现95%以上的准确率。为了更进一步的验证这两种算法的差异，对算法的收敛速度进行了比较，通过在搜索目标函数最优值过程中达到达到相同适应度值所需的迭代次数作为指标。

从图9中的随机收敛曲线可以看出，虽然PSBO算法寻优的收敛精度和PSO算法差不多，但是PSBO算法在收敛速度上明显有更好的表现力，在达到最佳适应值的目标上，PSBO算法能提高SBO算法4倍以上的收敛速度，进一步说明了PSBO算法应用于SVM参数优化的有效性。