基于多智能体强化学习的电力市场竞价模型
2022-01-26黄飞虎李沛东
黄飞虎,李沛东
(1.四川中电启明星信息技术有限公司,成都 610000;2.四川大学计算机学院,成都 610000)
0 引言
2015年国家针对电力体制改革发布了《关于进一步深化电力体制改革的若干意见》[1],该文件体现了国家对电力市场建设的重视和高瞻远瞩。文件说明了电力市场建设的目的,即打破现有的统一定价,通过市场竞争确定电价,充分发挥发电侧、售电侧、用电侧各个参与者的积极性,促进我国电力系统的发展。目前我国电力市场建设还处于初期阶段,截至2021年9月,我国已完成了第二批电力现货试点工作[2]。相比于国外的电力现货市场发展,我国的电力市场建设还有很多工作需要完善。
本文针对发电商参与电力现货市场竞价的场景,提出了基于多智能体强化学习的竞价模型,为电力现货竞价的研究人员提供参考。模型中,每个发电商抽象为一个智能体,具有动作空间和状态空间。考虑到竞价过程中,每个厂商对其他厂商的竞价策略以及市场出清结果的未知,模型采用了一种分散式学习算法,即Wolf-PHC,求解各发电厂商的最优策略。实验结果实证了本文模型的有效性。
1 相关工作
电力现货,即现货市场,是电力市场的组成部分。电力市场中除了电力现货之外,还包括中长期市场、容量市场、期货市场以及衍生品市场等[3]。现货市场涉及日前、日内、实时等短时间的电能交易。实时电能交易主要以小时为单位,主要解决超短期的电能缺乏和阻塞问题。现有的电力现货竞价策略可以分为三大类,一是基于成本的竞价策略,二是基于预测算法的竞价策略,三是基于博弈算法的竞价策略。
(1)基于成本的竞价策略是一类经典的方法。这类方法以经济学为基础分析发电成本,进而完成竞价。比如,文献[4]提出的报价策略主要考虑发电成本分析与系统边际电价之间的关系,其中系统边际电价通过预测算法得到。文献[5]通过分析机组在不同负荷下的发电成本,讨论了基于边际成本的竞价策略。
(2)基于预测算法的竞价策略。这类方法首先预测竞争对手的报价或者市场出清电价,然后作出竞价策略。比如,文献[6]则主要讨论单一水电厂参与的竞价问题,文中提出了基于市场出清电价预测的报价策略,策略主要约束条件是可用水量和机组特性。
(3)基于博弈算法的竞价策略。这类方法以博弈论、强化学习为基础,实现最优竞价策略。相比基于预测的竞价策略,这类方法具有更好的效果。博弈过程是参与者在相互作用中寻找最优策略的过程,这与电力市场参与者之间的竞价过程十分类似。因此,有一些学者基于博弈论构建竞价决策方法。比如,文献[7,8]对风光互补发电系统进行了竞标分析,将其建模为一个多人贝叶斯博弈问题,进而提出了基于贝叶斯博弈理论的竞价模型。强化学习因其扎实的理论基础,在很多应用场景(比如推荐系统、智能驾驶等)得到了应用。在电力现货中,也得到了学者们的广泛关注。比如,文献[9]将电力市场建模为信息有限的场景,提出了基于强化学习自动机的模型。模型中,作者利用重复博弈建模发电商与市场的反馈过程。文献[10]针对中长期电力市场发电商报价问题,采用A3C算法进行了建模仿真,并讨论了运营效率。
2 竞价模型构建
2.1 问题定义
报价策略算法的任务是给出合适的报价策略,实现利润最大化。从任务特点来说,发电厂商报价策略需考虑发电成本、机组出力等自身情况,推断日期(或实时)市场边界条件以及竞争对手的报价情况进而做出决策。从科学问题来说,报价任务可以定义为带约束条件的优化问题,即:

其中,约束条件包括机组运行特性(比如机组优先电量约束、机组出力上下限约束、机组爬坡约束等)、市场边界条件(比如线路潮流约束、断面潮流约束、电量空间边界等)。
2.2 模型描述
本文将各发电商建模为智能体,电力市场出清建模为环境,将发电商报价决策问题转化为一个多智体强化学习求解问题,如图1所示。各发电商根据发电成本、负荷需求和机组运行特性等约束条件给出最优报价。在交易中心收到所有发电商的报价之后,结合网络拓扑参数、潮流约束和负荷需求等因素进行出清,最后将出清结果反馈给各发电商。
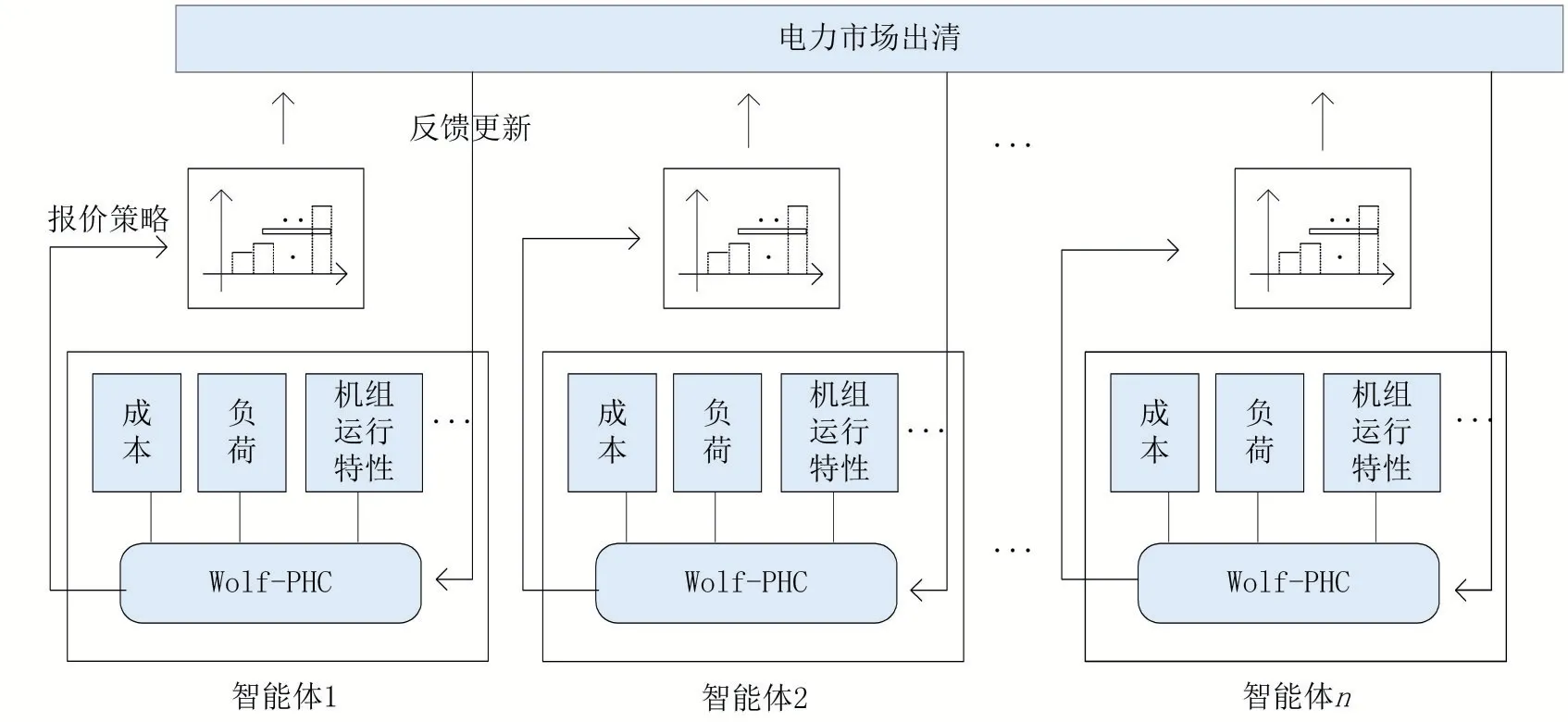
图1 模型框架
结合强化学习方法,相关定义如下。
定义1智能体。用集合G={g1,g2,…,gn}表示,在电力现货日前市场中,发电商i为一个智能体(即gi),各智能体之间具有竞争关系。
定义2动作。用集合A={a1,a2,…,an}表示,本文定义动作ai为发电商可选择的第i种报价曲线。
动作ai与发电商机组的出力区间相关,给定发电商的出力区间为[Pmin,Pmax],报价区间数为d段,则动作ai的报价曲线为:
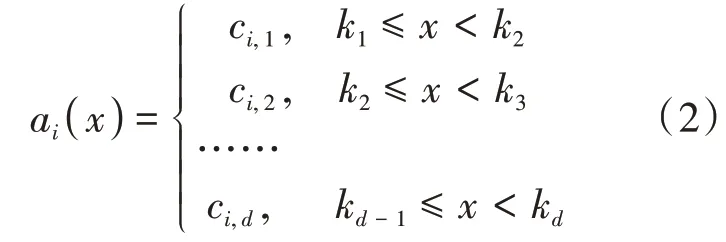
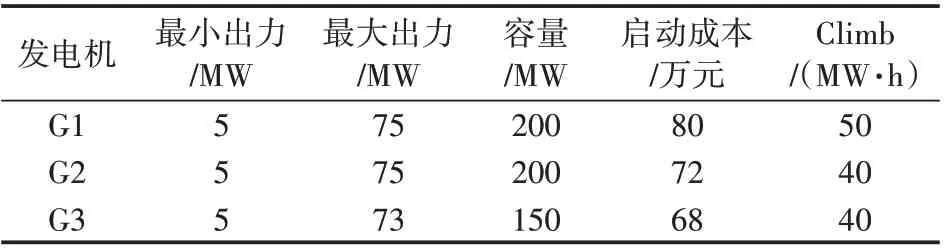
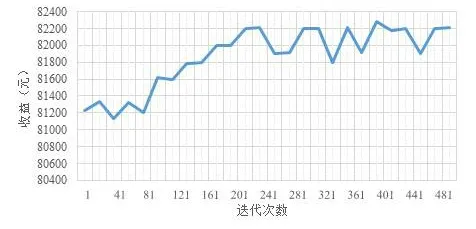
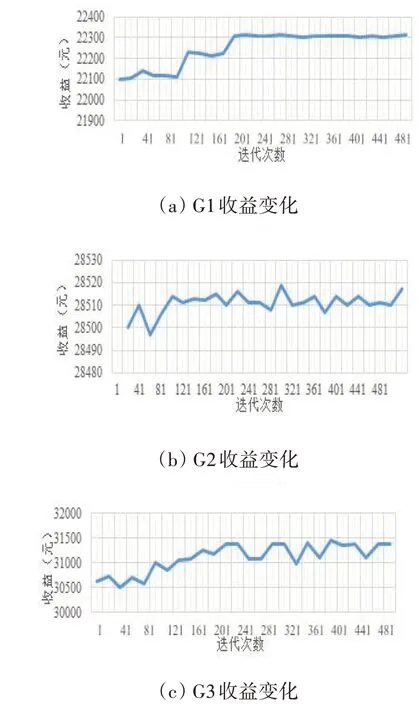
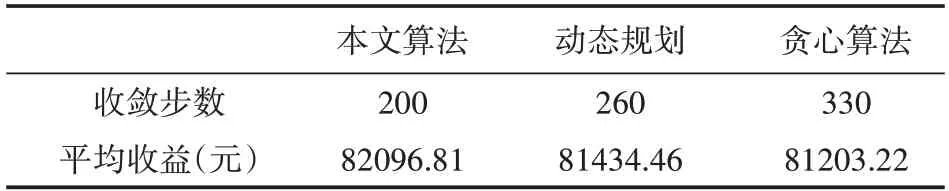
其中x表示出力,将出力区间[Pmin,Pmax]均分为d段,k1到kd为出力区间的分段标签,ci,∙表示对应区间的价格,满足ci,1≤ci,2 定义3状态。用集合S={s1,s2,…,s n}表示,本文定义发电商的出力情况为状态。 本文根据发电商的出力区间为[Pmin,Pmax]将状态离散化为n个区间,即S={[Pmin,P1),[P1,P2),…,[Pn-1,Pmax]}。 定义4回报。用r表示,本文定义回报即发电商报价后可以获得的收益。ri即智能体i在当前状态si下选择动作ai之后获得的收益。 不同类型的发电商有不同的发电成本,但计算方式均与中标电量、中标价格和成本相关。 定义5环境。用E表示,本文定义市场出清为环境,其决定各发电商在采取特定动作后的回报。 本文基于安全约束经济调度(SCED)进行出清,其公式如下: 其中,机组的总台数是N,总时段数为T,机组i在时段t的出力用pi,t表示,C i,t(pi,t)为机组i在时段t的运行费用,是与机组申报的各段出力区间和对应能量价格有关的多段线函数;网络潮流约束松弛罚因子用M L S表示;M C为机组优先电量约束松弛罚因子。公式中,针对电网安全问题,重点考虑了线路潮流和断面潮流的约束。首先,线路l在时段t的正、反向潮流松弛变量,即和;然后是断面s在时段t的正、反向潮流松弛变量,即sls+s,t,s l s-s,t;最后,考虑了机组i在时段t的机组优先电量松弛变量s l ci,t。 定义6策略。用π表示,其定义了一个特定时刻智能体的行为方式,即发电商在当前出力状态下该采取何种报价动作。 定义7状态-行为值函数。用Q表示,该函数刻画了智能体在长期状态下对于某个状态或者行为的偏好。 算法1智能体i的学习算法。 初始化: 学习率α=(0 ,1],δw∈( 0,1]且δl>δw; 折扣因子γ∈(0,1);探索率ε; 状态-行为值函数Qi(a)=0; 重复: (1)根据具有某一探索率ε的策略πi(a)选择报价动作并提交给市场。 (2)观测直接回报ri。 (3)更新Qt+1i(a),计算公式为: (4)更新策略πti+1(a),计算公式为: 其中, 在实际报价过程中,各发电厂商不知道其他竞争对手的策略,也不知道市场出清的信息,即回报函数。因此,本文采用Wolf-PHC算法求解报价最优策略。该算法中,各智能体只需知道自身的行为和每次获得的回报。在算法训练阶段,重复执行步骤(1)~(5)直至达到最大迭代次数或满足特定终止条件。当算法训练结束之后,则可以使用算法进行实际报价。 实验中地区的负荷数据,本文采用的数据集1数据集:https://www.eia.gov/electricity/gridmonitor/dashboard/electric_overview/US48/US48源于美国能源信息署的公开数据平台,本文下载了纽约市2015年7月—2021年4月的数据。数据间隔时间以小时为单位。训练过程中10天出清为一次迭代,每次迭代结束后记录各发电商10天的收益及所有发电商10天的总收益。 仿真实现对5节点3发电商系统进行模拟,每个发电商拥有一台火力发电机组,验证指标为每次迭代后的各发电商收益和总收益。设置的发电商机组信息如表1所示。 表1 发电商机组信息 每次出清发电商收益ri的计算公式为: 其中cost=a1(x‘)2+a2(x‘)+a3,x‘为中标出力,c‘为中标电价,a1,a2和a3分别是成本系数,实验中其设置信息如表2所示。 表2 成本系数设置 实验记录了总体的收益变化过程以及各发电商的收益变化过程,如图2和图3所示。 图2 总体收益变化 图3 各智能体收益变化 从实验结果来看,各发电商的收益随迭代次数增加,逐渐提高,最后达到稳定状态。这表明本文模型求解的最优策略能够使各发电商收敛到各自的纳什均衡状态。 此外,表3统计了本文模型与贪心算法、动态规划算法的收敛步数和收益比较。从实验结果来看,本文采用的基于Wolf-PHC求解算法,比动态规划和贪心算法具有更快的收敛速度,而且也能保证整个系统达到较大的收益。 表3 算法对比 针对电力市场的报价场景,本文提出了基于多智能体的强化学习报价策略。特别地,在策略求解时,针对各智能体无法知道对手策略以及回报函数的情况,提出了采用Wolf-PHC算法的思路。从实验结果来看,本文模型是可行的。在未来的工作中,本文作者认为应该从模型可信性的角度构建竞价模型。具有可信度高的模型,更容易让竞价操作者接受且认可模型给出的策略。从另一方面来说,现货市场的竞价涉及参与方的利益,因此只有可信度高的模型才能广泛用于辅助决策。2.3 模型训练

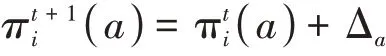
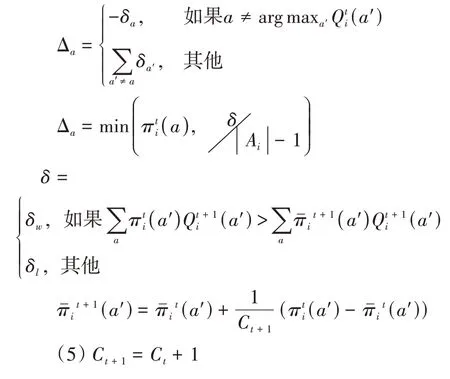
3 实验讨论
3.1 参数设置


3.2 结果分析
4 结语
