基于快速流式算法的局部余弦相似属性

周紫嫣，刘洋,刘财，王青晗，郑植升

吉林大学地球探测科学与技术学院，长春 130026

0 引言

相似性是认知科学中的一个基本概念，经常被用于解释认知过程，包括记忆检索、分类、视觉搜索等.另外，其也是计算机科学关注的一个基本的实际问题，涉及到聚类和机器学习等领域(Hahn，2014).相似性是一种常用的衡量不同图像之间差异程度的属性，在地球物理和遥感数据模式识别领域有着广泛的应用.Le Moigne等(2002)提出了基于区域相似性的遥感图像匹配方法.Buades等(2005)将基于图像相似性的非局部均值滤波应用于SAR图像去噪.Brunner等(2010)利用预测图像和地震发生后实际SAR图像的相似性判别建筑物在地震中的毁坏情况.Choi和Alkhalifah(2012)将全局相似性用于构建海上拖缆数据的多源波形反演的目标函数.Pan等(2013)将图像自相似性(Suetake et al.，2008)与压缩感知理论结合，提出了超分辨率遥感图像重建方法.毕丽飞等(2021)提出了基于特征相似性和地理相似性的半监督岩性预测算法.相似性也广泛用于很多地震数据处理环节，其可以定量地衡量两组地震数据的时间或空间方向上的差异，并用于构建对两组数据进行差异分析的特征(Jia and Lu，2020).然而，地震数据本质上在时间和空间方向表现出非平稳性，全局相似性很难刻画两个地震数据体之间的局部差异，因此，Fomel(2007a)提出了一种局部相似性的计算方法，其通过整形正则化条件迭代求解数学反问题进行局部差异的估计(Fomel，2007b)，这种属性被用于解决不同的地震数据处理问题.Liu等(2009)使用基于迭代计算的局部相似性进行加权叠加，有效提高叠加数据的信噪比.Fomel和Jin(2009)将迭代局部相似性用于时移地震数据匹配处理中，有效解决油气监测问题.Liu等(2010)将平面波预测和基于迭代计算的局部相似性权系数的非线性滤波方法结合，有效压制叠后地震随机噪声，突出地层结构信息.刘玉金等(2012)提出了基于迭代局部相似性的相位校正方法.Liu和Fomel(2013)在多波多分量地震数据匹配的过程中使用迭代局部相似属性进行波形拉伸函数选取.Gan等(2016)使用迭代局部相似性进行了同时震源混叠地震数据高分辨率速度分析.Dai等(2016)开发了一种基于迭代局部相似性的地震时变子波提取方法.相对于使用分窗处理算法(Claerbout，2013)，整形正则化能够更好地使局部相似性具有适应非平稳数据的时空变表征能力，避免固定分窗参数对非平稳相似性表征的局限.但是，随着高密度和宽方位角数据采集方案的实施，基于迭代算法的局部相似性计算需要占用大量的计算内存和计算耗时，限制了该方法在实际数据处理中的应用.

流式算法是一种适用于特殊形式大规模反问题的快速算法，通过递推的计算模式，使未知模型估计过程具备简单、计算效率高、可实时更新的特点.Fomel和Claerbout(2016)首先提出了用于解决地震勘探反问题的流式计算框架，在此基础上，Liu和Li(2018)提出了t-x域自适应流式预测滤波，并将其应用于解决地震随机噪声压制问题.Zheng等(2019)提出基于f-x域自适应流式预测滤波的地震数据插值方法.国胧予等(2020)提出了基于f-x域流式预测滤波器的地震随机噪声衰减方法.基于前期研究，本文提出一种基于快速流式算法的局部余弦相似性，并通过在叠前地震数据加权叠加、纵横波速度比估计和断层检测三个地震数据处理问题的应用效果，论述本文提出方法的有效性.

1 理论基础

1.1 局部余弦相似性

在相似性的计算中，基于向量空间模型的方法主要包括距离算法和相关系数算法，不同的相似性计算方法在衡量不同特征的数据差异时具有不同的特点：距离算法衡量的是空间各点的绝对距离，与各个点所在的位置坐标直接相关；而相关系数算法衡量的是空间向量的其他特征差异，例如，方向性等.比较常用的相关系数算法为余弦相关系数法，假设两个时间序列a(t)、b(t)，二者的全局余弦相关系数可以表示为

(1)

数学反演算法为计算局部余弦相似性提供了新的思路，在线性代数的形式下，离散信号的全局余弦相关系数可以表示为两个最小二乘解的乘积(Fomel，2007a)：

w2=pq，

(2)

p=(aTa)-1(aTb)，

(3)

q=(bTb)-1(bTa)，

(4)

其中，a、b分别是信号a(t)、b(t)的向量形式，aTb是它们的向量点积.为了得到随时间变化的局部余弦相似性系数，设A、B分别为向量a、b的元素构成的对角矩阵，并由方程(3)和(4)得到：

p=(ATA)-1(ATb)，

(5)

q=(BTB)-1(BTa).

(6)

Fomel(2007b)使用整形正则化算子对方程(5)和(6)进行平滑约束下的最小二乘求解，然后由p和q的逐点乘积再开方得到w，由此计算得到基于共轭梯度迭代算法的局部余弦相似性系数，迭代局部余弦相似性能够有效刻画非平稳数据的局部变化.

1.2 流式局部余弦相似性

迭代局部余弦相似性通过正则化最小二乘解得到，其计算过程需要多次迭代，尤其在计算多维大规模数据时，非平稳参数占用较大的存储空间，往往造成无法承受的计算量.为了提高局部余弦相似性的计算速度，本文提出基于流式算法的局部余弦相似性求取方法，使用流式算法给出的局部平滑约束条件下公式(5)和(6)的最小二乘解析解，避免多次迭代计算和全局平滑约束的条件.

只考虑相似性在时间方向的变化时，w为一维向量，用wi表示其元素.在一维的情况下，公式(5)和(6)可以写为

(7)

(8)

其中，pi和qi分别是向量p和q的元素.

本文引入局部平滑条件，使p的每个元素pi与相邻元素pi-1的数据值相近.局部平滑约束条件可以用方程表示为

(9)

其中，γ是约束p平滑性程度的常数惩罚因子.γ值应与数据振幅平方具有相同数量级，在将数据幅值进行归一化的前提下，γ可以在0到1之间选值.

加入局部平滑约束(9)的目标函数(7)可以用矩阵表示为

(10)

方程(10)的最小二乘解为

(11)

同样地，可以得到：

(12)

由于地震数据是时间和空间坐标的函数，相似性在二维t-x域中变化时，p则有时间和空间两个维度，用pi,j表示其元素.i、j分别是时间和空间上的采样序号.γt、γx分别是约束p在时间与空间方向平滑性程度的常数惩罚因子，此时公式(10)可以扩展为

(13)

其最小二乘解为

(14)

其中：

(15)

同理可以计算向量q.最终，局部余弦相似性系数向量w由向量p和q中对应元素逐点乘积再取开方运算获得：

(16)

需要注意的是，在公式(11)中，当数据ai的幅值近似为零时，p在该点处的更新量pi-pi-1也将近似为零，此时，该点处的局部相似性数值将与上一点相近，而不随数据幅值减少为零.对于公式(12)和(14)，当数据在该点的幅值近似为零时，也有相似的结论.为了使计算的流式局部余弦相似性能够反映出数据的零值部分，本文使用窗口分割数据，在每个窗口起点使用设定的初值进行初始化，在每个窗口内进行流式运算，在不同的应用中可以取不同的初值，突出高相似性时，取0为初值，突出低相似性时，取1为初值，例如，加权叠加和多波多分量纵横波速比估计应用中，取0为初值，断层检测应用中，取1为初值.此外，流式递推依赖于运算的方向，为了考虑到计算点两侧的平滑约束，可以采取将正向和反向计算的流式局部余弦相似性系数取平均值的方法.另外，流式局部余弦相似性可以直接推导出三维形式，此时局部平滑约束同时存在于时间t和两个空间x和y方向.与基于迭代的局部相似性算法(Fomel，2007a)相比，本文的流式局部余弦相似性算法在保证计算精度的前提下，计算成本上有较大程度的减少，具有更好的实用性，两种方法的计算成本如表1所示.接下来，将在叠前地震数据加权叠加、纵横波速度比计算和断层检测三个应用领域中阐述本文方法的实际处理效果.

表1 流式局部余弦相似性算法与迭代局部相似性计算成本对比Table 1 Comparison of computational costs between algorithms based on streaming local cosine similarity and iterative local similarity

2 实际应用

2.1 叠前地震数据加权叠加

叠加方法是地震勘探多次覆盖观测系统有效提高数据信噪比的核心，常规的叠加方法往往受制于各种叠加道集中的非同相叠加问题，为此，Robinson(1970)提出基于信噪比的加权叠加来提高常规叠加方法的噪声压制效果.本文将流式局部余弦相似性应用于叠前地震数据加权叠加，在提高叠加数据信噪比的同时提高计算效率.叠加的本质是均值滤波，其源于求解L2范数下的数学优化问题，并且主要适用于高斯分布的随机噪声压制.在地震勘探中，共中心点(CMP)道集水平叠加的基本方程为

(17)

其中，N是一个CMP道集上参与叠加的总道数，di,j(t)是第j个CMP道集中第i道上在双程走时为t的数据值.常规叠加方法的局限在于需要满足所有地震道中的噪声分量不相关，噪声呈正态分布，平稳且振幅相等(Mayne，1962；Neelamani et al.，2006).为了解决这个问题，Robinson(1970)提出了地震数据加权叠加的方法，Liu等(2009)改进了其方法，补偿了不同CMP道集之间的能量差异.本文使用的加权叠加方程为

j=(1,2,3,…,M)，

(18)

其中，wi,j(t)是第j个CMP道集中第i道上t时间的权重.由于地震道中不同的反射波具有时变特征，因此在不同反射时刻的叠加权系数应该具有时变特征，为了使加权叠加适用于地震数据的非平稳性，可以选取流式局部余弦相似性系数作为加权叠加的权重，首先使用常规叠加方法得到初始叠加参考道，再计算参考道与每一道数据之间的时变流式局部余弦相似性系数，最后进行加权叠加.另外，本文方法还适用于共反射点(CRP)等其他道集的叠加处理.

为了验证流式局部余弦相似性加权叠加方法，首先使用Kirchhoff正演方法构建包含四个反射同相轴的二维测线叠前模型数据(Liu et al.，2009)进行测试.其中添加的高斯随机噪声分布为N(μ,σ)=N(0,0.05).为了定量地衡量信噪比的效果，使用公式(19)进行分析：

(19)

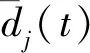
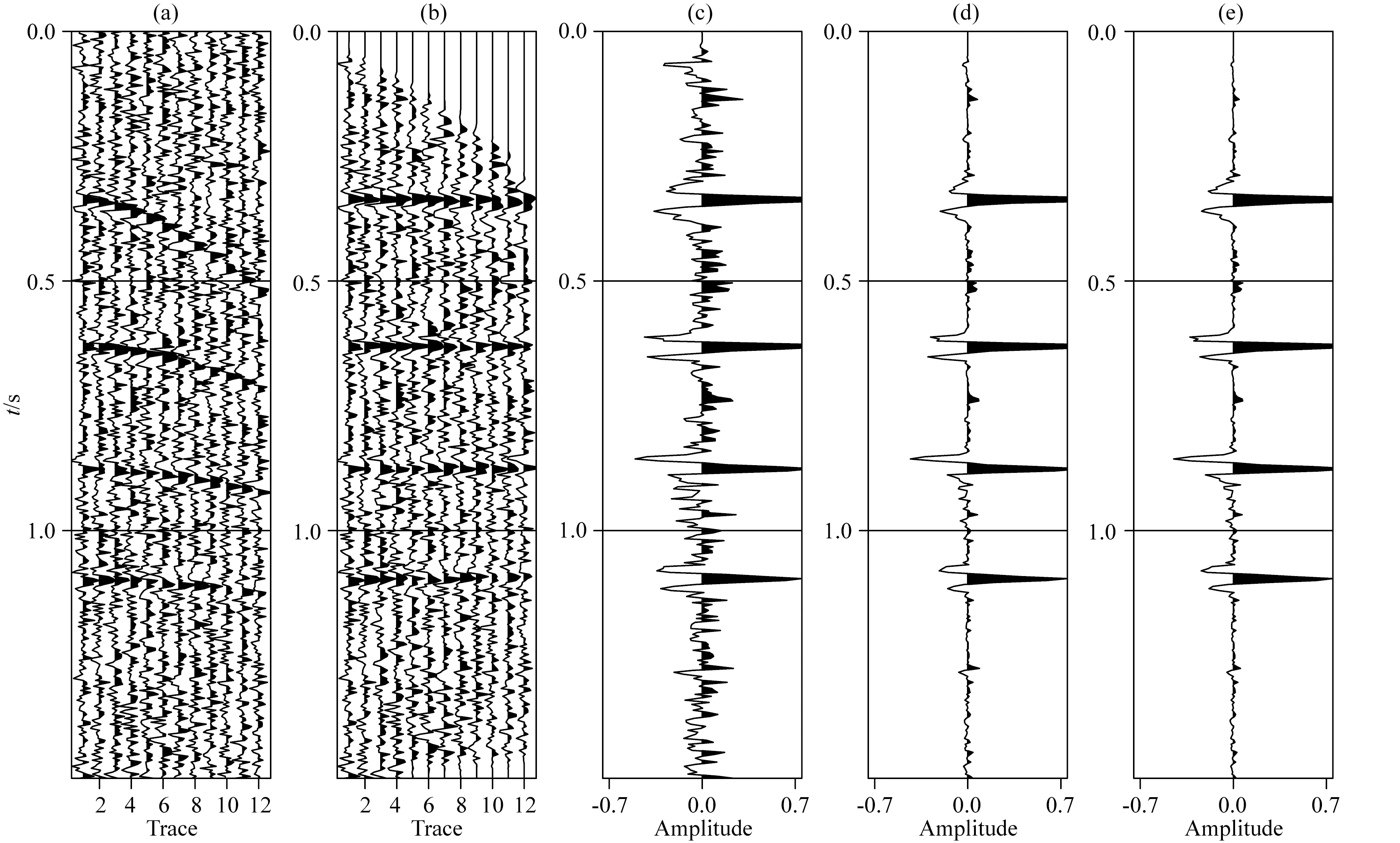
图1 CMP道集叠加结果对比(a)带噪声的CMP道集；(b)NMO校正后道集；(c)常规叠加结果；(d)迭代局部相似性加权叠加结果；(e)二维流式局部余弦相似性加权叠加结果.Fig.1 Comparison of stacking results for a single CMP gather(a)Noisy CMP gather;(b)Gather after NMO correction;(c)Conventional stacking result;(d)Iterative local similarity weighted stacking result;(e)Weighted stacking result with 2D streaming local cosine similarity weight.

图2 叠加剖面对比(a)常规叠加结果；(b)迭代局部相似性加权叠加结果；(c)二维流式局部余弦相似加权叠加结果.Fig.2 Comparison of post-stack sections using different stacking method(a)Conventional stacking result;(b)Weighted stacking result with iterative local similarity weight;(c)Weighted stacking result with 2D streaming local cosine similarity.

接下来，使用某地区实际陆上地震数据进行测试，NMO校正之后的CMP道集数据如图3a所示.由于参与局部相似性系数计算的参考道数据质量对加权叠加结果有影响(Sanchis and Hanssen，2011)，将常规叠加结果经简单的高斯滤波平滑处理后作为参考道，用于流式局部余弦相似性加权叠加的权重数据体如图3b所示.分别用常规叠加、迭代局部相似性加权叠加和流式局部余弦相似性加权叠加对CMP道集数据进行叠加处理，三种方法的计算耗时分别为1.4s、82.2 s和6.4 s，叠加结果如图4所示.从图4可以看到，本文的流式局部余弦相似性加权叠加方法能够更加有效地压制噪声，并保留有用信号的幅值，使叠加剖面中的地层界面更加清晰.

图3 实际陆上地震数据体及加权叠加权重数据体(a)NMO处理后的叠前CMP道集；(b)流式局部余弦相似性加权叠加权重数据体.Fig.3 Real land-based seismic data body and weighted stack data body(a)CMP gathers after NMO processing;(b)Weighted data body based on streaming local cosine similarity.

图4 实际数据叠加结果对比(a)常规叠加结果；(b)迭代局部相似性加权叠加结果；(c)二维流式局部余弦相似性加权叠加结果.Fig.4 Comparison of stacking results of real data set(a)Conventional stacking result;(b)Weighted stacking result based on iterative local similarity;(c)Weighted stacking result based on 2D streaming local cosine similarity.

2.2 多波多分量数据纵横波速度比估计

多波多分量地震勘探可以提供纵横波时差、频率、速度比等信息，以减小单一纵波勘探的非唯一性(Stewart et al.，2003).Fomel等(2005)提出了一套多波多分量数据匹配的处理流程，包含初始标定、谱均衡、剩余γ扫描以及最小二乘优化四个步骤，Liu和Fomel(2013)对其进行改进，通过局部时频分解方法对多波数据进行谱均衡处理，使该处理流程更适用于非平稳地震数据，本文将流式局部余弦相似性应用于多波数据匹配中，主要步骤如下：

(1)初始标定：使用初步的地震解释以及已知的井资料，确定初始形变函数及纵横波速比初始值；

(2)谱均衡：由于纵横波的波速和在地层中的衰减特征不同，在局部时频分解(Liu and Fomel，2013)域中对多波多分量数据进行能量谱均衡；

(3)剩余γ扫描：γ是纵横波速度比，剩余γ即参数γ0，通过扫描拾取参数γ0并更新形变函数；

(4)在最小二乘约束下使用形变函数对多波数据进行拉伸或压缩；

(5)若满足迭代停止条件，输出匹配结果，计算并输出纵横波速比；否则，返回步骤(2).

步骤(3)中，剩余γ扫描的目的是对已经完成初始标定和谱均衡后的纵、横波数据进行剩余的拉伸或压缩，其实现过程如图5所示.从剩余γ扫描的结果可以最终估算地层的纵横波速度比.在整个流程中，局部相似性方法用于实现γ0参数的计算，但是由于原有的迭代局部相似性算法在进行γ0参数估计时需要大量的计算时间，限制了该处理流程的工业实用化，因此，本文使用流式局部余弦相似系数提高剩余γ扫描的计算速度，更加适用于高维多波多分量地震数据的非平稳纵横波速度比参数估计.

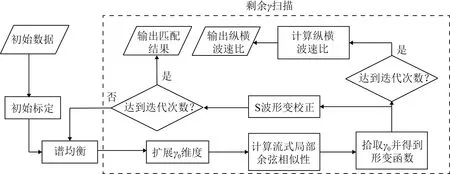
图5 剩余γ扫描过程Fig.5 Flow chart of residual γ scanning

在多波多分量数据匹配的过程中，当完成纵横波初始标定和谱均衡后，横波和纵波数据具有近似的时间一致性.为了进行精确匹配，用γ0来表示横波数据的形变程度，γ0即剩余γ，取值在1.0左右，使用扫描的方式得到γ0(t,x).首先扩展γ0维度，将完成初始标定和谱均衡的横波数据使用不同的γ0在时间方向进行拉伸或压缩变形，然后，计算纵波数据与扩展γ0维度后的横波数据之间的流式局部余弦相似性，通过提取局部相似性最大值点来拾取γ0(t,x).γ0=1时横波数据不进行剩余形变校正，γ0>1时横波数据进行剩余压缩校正，γ0<1时横波数据进行剩余拉伸校正.横波数据的形变校正由随时间和空间变化的形变函数warp(t,x)实现(Wolberg，1990；Hale，2013a)，同时，由形变函数可以估算地层纵横波速比γ(t,x)(Gaiser，1996)：

P(t,x)≈A(t,x)S[warp(t,x)]，

(20)

(21)

其中，P(t,x)为纵波数据，S[warp(t,x)]由横波数据S(t,x)形变校正得到，A(t,x)是补偿反射系数差异的幅度增益函数，可在已知P(t,x)和S[warp(t,x)]情况下对式(20)进行正则化最小二乘求解得到.由公式(21)可见，γ(t,x)仅与形变函数对时间的导数有关.

使用实际陆上多波多分量地震数据对本文方法及流程进行测试.对比图6中纵横波地震剖面可以观察到，同一地层在纵横波剖面中具有不同的地震波走时，而且分辨率和能量均有较大的差异，多波匹配能够更好地实现纵横波数据的联合解释.基于本文流式局部余弦相似性的剩余γ扫描技术能够获得与图7a所示迭代法类似的局部相似属性体，如图7b所示.从图中可以看到，局部相似性值在时间和空间方向具有明显的变化，有效地表征纵横波速度差异的非平稳性.图8为多波数据匹配前后的混波剖面.从图中白框部分可以看到，混波剖面中同一反射层面的连续性明显提高，说明数据匹配流程的有效性.相比迭代局部相似性算法，流式局部余弦相似算法进行剩余γ扫描所需时间更短，在单核2.10 GHz CPU的计算条件下，迭代局部相似性方法和本文方法的计算时间分别为42.5和4.4 s，本文方法在该实例中节约大约90%的计算时间.最终，初始的常数纵横波速度比(图9a)通过数据匹配，能够获得时空变化的纵横波速度比分布图(图9b)，为描述地下介质的岩石弹性性质提供有用的信息.

图6 多波多分量陆上地震数据(a)PP波；(b)SS波.Fig.6 Multi-component land seismic data(a)PP-waves;(b)SS waves.

图7 用于剩余γ扫描的局部相似性数据体(a)迭代局部相似性数据体；(b)流式局部余弦相似性数据体.Fig.7 Local similarity data body for residual γ scanning(a)Iterative local similarity;(b)Streaming local cosine similarity.

图8 匹配前后纵横波混波剖面对比图(a)匹配前；(b)匹配后.Fig.8 Interleaved traces from PP and warped SS waves(a)Before registration;(b)After registration.

图9 纵横波速度比分布(a)初始的纵横波速度比；(b)匹配得到的纵横波速度比.Fig.9 Distribution of VP/VS ratios(a)Initial VP/VS ratio;(b)VP/VS ratio after data registration.

2.3 叠后断层检测

断层位置的识别对于理解地下结构和成藏机制尤为重要，很多学者提出了有效的断层检测方法.Hale(2013b)以及Wu和Zhu(2017)使用扫描所有可能的断层走向和倾角并拾取最大响应的方法来估计断层的走向和倾角，并用获得的结果增强断层信息.Qi等(2017)提出了一种针对多方位角地震数据的能量比一致性算法，用于横向各向异性区域的断层识别.Wu和Fomel(2018)首先在控制点周围提取断层信息，再使用最优投票算法进行断层识别.Yuan等(2019)在瞬时频率属性的基础上提出了地质导向相位属性，并将其应用于三维地震图像的断层识别.冯琦等(2021)利用优选地震属性技术提高小断层识别精度，将其应用于鄂托克前旗地区，并取得了良好效果.尽管有大量的新方法被用于断层检测，但主流的断层检测技术仍然依赖于相干体属性，而传统的基于滑动窗口的相干体属性往往难以处理断层的局部变化特征.

消除弯曲同相轴的影响是断层检测方法的重要前提.基于地震局部倾角的构造预测方法能够实现不同道距间地震道的预测，利用不同预测步长条件下的预测数据即可组成高一维度的预测数据体(刘洋等，2014)，断层信息一般在时空方向不可预测，构造数据体中预测数据与原始数据之间数值的差异可以用于指示断层的位置，由于较大的预测距离会降低构造预测的准确性，因此在断层检测中仅选取一个预测步长(二维数据使用2个相邻道，三维数据使用8个相邻道)，最后计算预测地震道与原始地震道之间的局部相似性系数，并且沿预测步长方向叠加即可获得合理的断层位置，基于构造预测的断层检测流程如图10所示.

图10 基于构造预测的断层检测示意图Fig.10 Schematic illustration of fault detection based on structural prediction

选取墨西哥湾某地区的三维叠后数据体进行构造断层的检测，图11a为带有一个倒圆锥形状断层的原始数据.为了充分利用三维数据中两个空间方向的信息，选取共8个预测地震道(每个当前道周围1个预测步长距离的地震道)，组合形成一个四维数据体，此时的构造预测需要同时使用主测线和联络测线方向的同相轴倾角，流式局部余弦相似性系数可以有效表征原始数据与其预测数据的差异，沿着预测步长方向对相似性系数进行叠加平方计算可以突出断层位置.使用迭代局部相似性和流式局部余弦相似性指示的断层位置如图11b和图11c所示.在单核2.10 GHz CPU的计算条件下，基于迭代局部相似性算法的断层检测(刘洋等，2014)计算时间为147.0 s，基于本文方法的断层检测计算时间为39.3 s，本文的流式局部余弦相似性算法能够为更大规模叠后地震数据的构造解释提供高效的断层位置估计方法.

图11 自动断层检测结果(a)三维叠后地震数据；(b)迭代局部相似性指示的断层位置；(c)流式局部余弦相似性指示的断层位置.Fig.11 Result of automatic fault detection(a)3D seismic data after stacking;(b)Fault position indicated by iterative local similarity;(c)Fault position indicated by streaming local cosine similarity.

3 结论

为了计算不同地震数据体之间的差异性，本文提出了一种基于快速流式算法的局部相似性计算方法，这种流式局部余弦相似属性能够有效刻画地震数据间波形差异的非平稳时空变化特征.通过引入局部平滑约束条件，可以直接计算局部余弦相似性系数方程的最小二乘解，避免由全局平滑约束条件引起的迭代计算，在保证非平稳差异合理性的同时有效提高计算效率，更加适用于高维地震数据体间局部相似程度的表征.本文方法的高效性和准确性能够支撑流式局部余弦相似属性用于多种地震数据处理任务，理论模型和实际数据的处理结果表明，流式局部余弦相似属性可以有效解决叠前地震数据加权叠加、多波多分量地震数据地层纵横波速度比估计和叠后断层检测，保证地震数据间差异的非平稳性和计算效率.另外，本文方法还适用于其他基于相似性的地震数据处理问题，例如地震子波相位校正等.

致谢感谢Texaco公司提供的墨西哥湾三维叠后地震数据，感谢两位匿名审稿专家提出的宝贵意见.