绕射波逆时偏移成像方法研究
2022-01-25王晓毅陈玺杨振张江杰
王晓毅,陈玺,杨振,张江杰
1 中国科学院地质与地球物理研究所,中国科学院油气资源研究重点实验室,北京 100029 2 中国科学院地球科学研究院,北京 100029 3 南方海洋科学与工程广东省实验室(广州),广州 511458 4 广州海洋地质调查局,广州 510075 5 中国科学院大学,北京 100049
0 引言
地下介质中广泛发育的断层、尖灭、溶洞等中小尺度不连续体,对油气生成、运移和存储具有重要意义.由于绕射波的形成与裂缝等构造相关联(黄建平等,2015;栾锡武和李继光,2018),其可以作为偏移处理对象来对目标地质体进行精细成像.
目前,相关研究主要集中在如何利用绕射波与反射波在运动学上的区别进行波场分离与成像.常规的绕射波成像技术以射线类偏移方法为主.其中,针对绕射波较强的情形,对地震数据采用绕射增强的叠加算法是一种有效的策略(Faccipieri et al.,2016),但其难以处理能量较弱的绕射波.利用反射波和绕射波不同的运动学特征,在地震资料中对二者进行分离,同样能够达到成像的目的(Merzlikin and Fomel,2017;Rad et al.,2018).然而,当地下介质构造复杂时,反射波在变换空间的形态不再简单,极大地提高了分离的难度.此外,还可以在偏移道集中区分绕射波和反射波(Zhang and Zhang,2014),该类方法对复杂反射具有很好的适应性,但对于深度域三维成像而言,其运算成本较高.Li和Zhang(2019)提出基于反稳相偏移产生的时差道集来甄别和增强绕射波信号,该方法要求地层倾角信息精确,不需要过大内存就可实现绕射波成像.
射线类方法在提取地震波的传播方向和走时上具有灵活简便的优点,但在复杂构造区域的成像上往往效果有限.基于此类方法的绕射波成像虽然提高了绕射体的成像分辨率,但其成像位置的准确性难以满足要求.利用波动类方法进行绕射波成像精度较高,需要的计算成本也较大.例如,Liu等(2016)借助相移插值(PSPI)法提取倾角道集,并通过中值滤波实现了绕射点成像.逆时偏移作为一种经典的波动方程类成像方法,具有诸多优点,如不受地层倾角的限制,能够灵活处理回转波和棱柱波等.根据波传播射线的几何特征,选择不同的波场组分进行互相关运算,可以实现对某一类构造的单独成像(王一博等,2016;Zhang et al.,2019a,b).当入射波沿右下方传播而出射波沿左上方传播时,反射界面是正倾角的地层;入射波沿左下方传播并且出射波沿右上方传播时,反射界面是负倾角地层.由于在不连续点处产生的绕射是沿各个方向的,因此在多种成像条件下绕射波的能量都可以得到聚焦.Zhang等(2019a,b)通过一种乘法成像条件(the multiplication imaging condition),利用正倾角地层剖面和负倾角地层剖面相乘得到单独的绕射点位置剖面.这一方法较为简单,但偏移剖面只包括位置信息,忽略了同相轴的幅值和相位信息.
本文基于逆时偏移对绕射波能量进行聚焦,运用多种方法得到单独的绕射点剖面.首先,本文详细分析了绕射波和反射波的运动学特征以及各种成像方式的特殊性.借助Hilbert变换波场和Fourier变换,实现波场分离.基于此,我们获取了单一倾向构造的成像剖面以及更高质量的倾角域共成像点道集.随后,我们通过乘法成像条件获取了单独的绕射点剖面并在倾角域拾取了绕射波能量.此外,我们还对无需波场方向分解的正负倾角构造成像公式进行了推导,并提出了一种在成像剖面上快速获取绕射点信息的方案.
1 基本理论
目前,基于逆时偏移对绕射点和间断点实现定位的策略分为以下两种:选择不同的震源波场和检波器波场组分互相关以得到正倾角和负倾角地层构造,相乘获取单独的绕射点剖面(Zhang et al,2019a,b,2020);逆时偏移产生共成像点倾角道集,然后在角道集中甄别、拾取绕射波能量(汪天池等,2020).以上两种方案中,选择合适组分和提高角道集质量都可以利用Hilbert变换实现波场分离.
1.1 Hilbert变换与波场分解
在频率-波数域中,根据圆频率ω和波矢量k的符号,可以将原始波场按照传播方向分解为若干个分量.在二维情形下,将时间-空间域的波场转化到频率-波数域需要三维傅里叶变换.其中,沿时间轴方向的傅里叶变换需要用到所有时刻的波场快照,这极大地增加了存储成本并制约了运行效率.
通过Hilbert变换对原始信号进行改造,可以只保留频谱和振幅谱中的正频率部分.图1a是均值为0.25,方差为0.02的高斯子波信号,其振幅谱和相位谱分别如图1b蓝色线和橙色线所示.将原始信号进行Hilbert变换之后,得到以原始信号为实部,图1c中橙色线段为虚部的复数信号.图1d是复数信号所对应的振幅谱(蓝色线)和相位谱(橙色线),可见复数信号在负频率部分振幅为0,正频率部分振幅扩大为原来2倍.换言之,Hilbert变换使信号只保留正频率部分.将这一性质应用于波场分解,可以避免圆频率ω符号的判断,从而减少沿时间轴方向波场的存储.

图1 原始信号与其经Hilbert变换之后得到的复数信号(a)原始信号:均值为0.25,方差为0.02的高斯子波;(b)与信号(a)对应的振幅(蓝色线)和相位谱(橙色线);(c)复数信号:以原始信号为实数部,以Hilbert变换后信号为虚数部(如橙色线段所示);(d)与复数信号(c)对应的振幅(蓝色线)和相位谱(橙色线).注意振幅在负频率部分为0.Fig.1 The original signal and the complex signal obtained after the Hilbert transform to it(a)The original signal:a Gaussian wavelet with mean value of 0.25 and variance of 0.02;(b)The amplitude and phase spectrum (blue and orange lines)corresponding to the signal (a);(c)The complex signal:taking the original signal as the real part and the Hilbert transformed signal (the orange line)as the imaginary part;(d)The amplitude and phase spectrum (blue and orange lines)corresponding to the signal (c).Note that the amplitude is zero in the negative frequency part.
对于声波而言,标量波动方程可以表述为
(1)

(2)

(3)
在这里,i=lu,ru,ld或者rd分别表示左-上行波,右-上行波,左-下行波和右-下行波.四者对应的积分区域(kmin,kmax)分别为((0,-∞),(+∞,0)),((-∞,0),(0,-∞)),((+∞,0),(0,+∞))和((0,+∞),(-∞,0)).Re{·}表征取实数部算子.显然,公式(3)也可以通过空间域Hilbert变换实现.需要特别指出的是,尽管我们在论述的过程中选用的是标量声波方程,使用一阶速度-应力方程同样可以先对震源进行Hilbert变换后延拓得到伴随波场,再实现波场分解.
1.2 针对不同地层结构的成像条件
逆时偏移作为一种基于双程波动方程延拓的方法,成像结果往往受低频噪音以及偏移假象的影响.解决这一问题的途径之一是在成像条件中只保留下行震源波场和上行检波器波场的互相关(Claerbout,1971;Fei et al.,2015),即

(4)
其中,s和r分别表示震源波场和检波器波场,下标u和d则分别代表上行和下行方向,tmax是最大记录时间.按照波的传播方向,震源波场和检波器波场除了可以分为上下组分之外,还可以进一步分为左右组分,即sd=sld+srd,ru=rlu+rru.因此,(4)式又可以进一步写为
(5)
利用震源波场和检波器波场不同组分之间的互相关,可以实现对单一倾向的地质构造的成像.图2a是一正倾角地层,地震波从震源激发向右下方向传播至界面,沿左上方向发生反射并被地表检波器接收.与之对应,对于负倾角地层,地震波是向左下方传播而反射波则沿右上方向传播至检波器,如图2b所示.不同于倾斜的连续反射界面,绕射点可以同时满足两种情况下的入射波和反射波的方向特征.换言之,如果我们利用(5)式的第一项I1(x),则只有正倾角地层和绕射点被成像;如果利用(5)式的第二项I2(x),则只有负倾角地层和绕射点被成像.进一步地,针对绕射点定位的乘法成像条件被提出(Zhang et al.,2019a,b),即

图2 针对正倾角(a)和负倾角(b)的地层构造,入射波与出射波之间的关系Fig.2 The relationship between the incident wave and the outgoing wave for the formation structure with positive dip angle (a)and negative dip angle (b)
(6)
在这里,ns表示总炮数.
不同于前两者,采用I3(x)和I4(x)得到的构造剖面没有特定性,无论正、负倾角地层、平界面或者绕射点,都可能被成像.并且由互易性定理可知,当观测系统对地下介质能够充分覆盖时,I3(x)和I4(x)的成像结果具有很好的相似性.
为了更好地利用多次波、回转波、棱柱波等波型,我们还可以采用Causal成像条件(Liu et al.,2011;Li et al.,2019),即

(7)
与之对应,有


(8)
不同于(5)式,上式中的成像条件可以在不显式对波场方向分解的情况下实现.经过推导(详见附录),(8)式可以写为

(9)
其中
(10)

(11)
1.3 高质量倾角道集的提取
在地震资料处理中,角度域共成像点道集具有十分重要的作用.在张角域,反射波和绕射波信号之间没有明显的区别,因此区分二者能量比较困难.但是在倾角域,反射波能量只集中在地层的真实倾角附近,而绕射波的能量则连续分布在一定的范围内.所以,通过先提取倾角道集再拾取绕射波能量的方式,可以凸显绕射点的正确位置.Jin等(2014)将基于逆时偏移计算角道集的方法总结为三类:方向矢量法(DVB),局部平面波分解法(LPWD)和局部相移成像条件法(LSIC).其中,方向矢量法运算量少,方便快捷,并且结果分辨率高.为此,我们采用Poynting矢量法计算共成像点倾角道集.
本文选择声波方程的一阶速度-应力形式对波场进行延拓,因此Poynting矢量可以直接由速度和应力之积得到,即
p=-τv,
(12)
在这里,p表示Poynting矢量,τ表示应力张量.v表示质点的运动速度矢量.Poynting矢量的幅值代表能流密度的大小,其方向指向波的传播方向.由(12)式可知,对于任意一个空间位置,Poynting矢量只能给出一个传播方向.所以在波发生重叠的区域,例如强反射界面附近,计算得到的角度准确性不足.
利用Hilbert变换伴随波场,首先将原始声压场和质点速度分量分离为沿不同方向(左上,左下,右上和右下)的组分,再使用(12)式分别获取不同波精确的传播方向.虽然波场分解增加了方案的复杂度和运算量,但能够避免由波重叠引起的Poynting矢量不准确的问题,从而提升倾角道集的质量.
图3描述了波由震源出发,在界面处发生反射最终被检波器接收的过程.假设在成像点处发生反射,利用震源波场Poynting矢量ps和检波器波场Poynting矢量pg可以计算出地层倾角α,即

图3 倾角计算的几何示意Fig.3 Geometric diagram of the dip-angle calculation
(13)
在偏移过程中,将每个时刻震源波场和检波器波场的互相关值叠加到成像点对应的α处即可得到共成像点倾角道集.
在倾角道集中,甄别、拾取绕射点能量既可以人工操作,也可以利用中值滤波等方法来自动实现.值得注意的是,绕射能量也会受到偏移孔径的影响,对于有限的空间采样,绕射点埋深越大,其在倾角域分布的范围越窄.而窄化的绕射点能量会弱化和反射点之间的区别,增大绕射点成像的难度.
1.4 成像后绕射点定位
前两种方案都是以逆时偏移为基础,根据地震波遇到不同地质构造时射线路径的特征,实现绕射点定位和能量聚集的.因此,它们的过程相对复杂,存储成本较高,运算量成倍增加.如果能够直接在成像剖面上拾取绕射点和间断点,方法将不局限于逆时偏移技术,且效率也会有效提升.目前,已有相关研究展开.例如,奚先和黄江清(2020)通过卷积神经网络(CNN)实现了在地震剖面上散射体的定位和成像.本文提出另一种简单直接的绕射点定位方案.

(14)

与式(6)相同,我们采用乘法成像条件获取单独的绕射点成像剖面,即
Idif(x)=I+(x)·I-(x).
(15)
显然,本方案与方案一相比所需的运算量较少、可以对工区剖面做局部化运算、也不局限于逆时偏移所产生的地震剖面.
这里我们给出一个简单的实例.图4a是输入图像,包括左倾、右倾、水平和竖直四条线段和一个孤点.图4b是与4a相对应的振幅谱,按照kx·kz≥0和kx·kz<0,我们分别得到了图4c和4d.进一步,经过反傅里叶变换,我们得到了如图4e和4f的构造.需要注意的是,在图4e中,除了倾角为正值的线段和孤点,还包括连续的水平线段和垂直线段,这是因为我们在其波数域中保留了kx·kz=0的区域.对于实际的地震剖面,为了避免在较平缓界面或者接近垂直的构造处成像,我们会在波数域kx和kz接近0的位置将值设置为零.最后采用(15)式乘法运算,我们得到了孤立点以及唯一的交叉点的位置,如图4g中红圈所示.

图4 原始输入图像,不同构造分离和绕射点成像图(a)是原始图像,包括不同倾向的线段和绕射点.图(b)是与图(a)相对应的幅度谱,按照(14)式可分为图(c)和(d).经过反傅里叶变换,可得图(e)和(f).进一步,按照乘法成像条件可得同时包含交叉点和孤点的最终剖面(g).Fig.4 Original input image,separation of different structures,and imaging of diffraction pointsPanel (a)is the original image,including line segments with different inclinations and an isolated point.Panel (b)is the amplitude spectrum corresponding to figure (a),which can be divided into panels (c)and (d)according to equation (14).After the inverse Fourier transform,panels (e)and (f)can be obtained.Furthermore,by using the multiplication imaging condition,we have a final profile (g)containing both an intersection point and an isolated point.
2 数值算例
为了验证上述理论的正确性和方案的可行性,我们在简单模型和Marmousi2模型上分别进行了实验并对结果进行了展示.
2.1 简单模型
在此模型中,我们设置了正、负倾角反射面、平界面以及三个绕射点,如图5所示.40个炮点在地表均匀分布,间隔设为75 m,检波器则分布在整个地表,间隔设为5 m.震源选择为主频30 Hz,时间采样间隔0.5 ms的雷克子波.地震数据由时间二阶、空间八阶的有限差分算法模拟得到.该实验选择3000 m·s-1的均匀模型作为偏移背景速度.
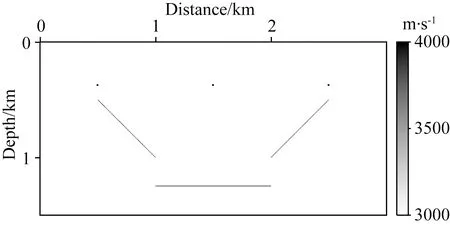
图5 简单模型,其中包括正负倾角界面,平界面以及三个绕射点Fig.5 A simple model.It includes positive-and negative-dip interfaces,a flat interface,and three diffraction points
在震源波场和检波器波场中分别选取不同的组分采用互相关成像条件,可以得到不同的成像结果.图6a和6b分别对应式(5)中的I2(x)和I1(x),即分别对负和正倾角构造进行了成像.除了连续界面,绕射点或者不连续点在剖面上也有所显示.通过I1(x)和I2(x)剖面相乘,可以获取只包含绕射点位置的成像结果,即图6f.另外,我们在图6c和6d中展示了I3(x)和I4(x)所对应的剖面,由于震源点和检波器点之间的互易性,两者有一定的相似性.特别地,我们计算了以(4)式作为成像条件的剖面Isum(x),如图6e所示.按照第三种方案,我们采用获取到的完整剖面作为输入,分别提取了负倾角构造和正倾角构造,如图7a和7b所示.应当注意的是,我们在波数域的分离避开了波数分量为0的区域,从而避免了单一倾角构造剖面上的平界面的出现.最后,通过乘法成像条件,获取了图7c中的绕射点剖面.从图中可见,方案一和方案三在简单的模型上的绕射点定位结果基本一致.图8a和8b是按照成像条件(11)得到的负倾角和正倾角剖面,在求取过程中需对震源波场和检波器波场进行Hilbert变换,而无需伴随波场的延拓和原始波场的方向分解.图8c是由图8a和8b得到的绕射点剖面.

图6 简单模型不同成像条件下的成像结果(a)是负倾角构造,与成像条件I2(x)对应;(b)是正倾角构造,与成像条件I1(x)对应;(c)和(d)分别是在成像条件I3(x)和I4(x)下的剖面;(e)完整的成像剖面;(f)绕射点剖面,为(a)和(b)的乘积.Fig.6 Imaging results of the simple model under different imaging conditions(a)is the negative-dip structure,which corresponds to the imaging condition I2(x);(b)is the positive-dip structure,which corresponds to the imaging condition I1(x);(c)and (d)are the profiles under imaging conditions I3(x)and I4(x),respectively;(e)is the complete profile;(f)is the profile of diffraction points,which is the product of (a)and (b).

图7 简单模型按照方案三得到的成像剖面(a)负倾角构造;(b)正倾角构造;(c)绕射点剖面,为(a)和(b)的乘积.Fig.7 Imaging profiles of the simple model obtained from scheme 3(a)The negative-dip structure;(b)The positive-dip structure;(c)The profile of diffraction points,which is the product of (a)and (b).
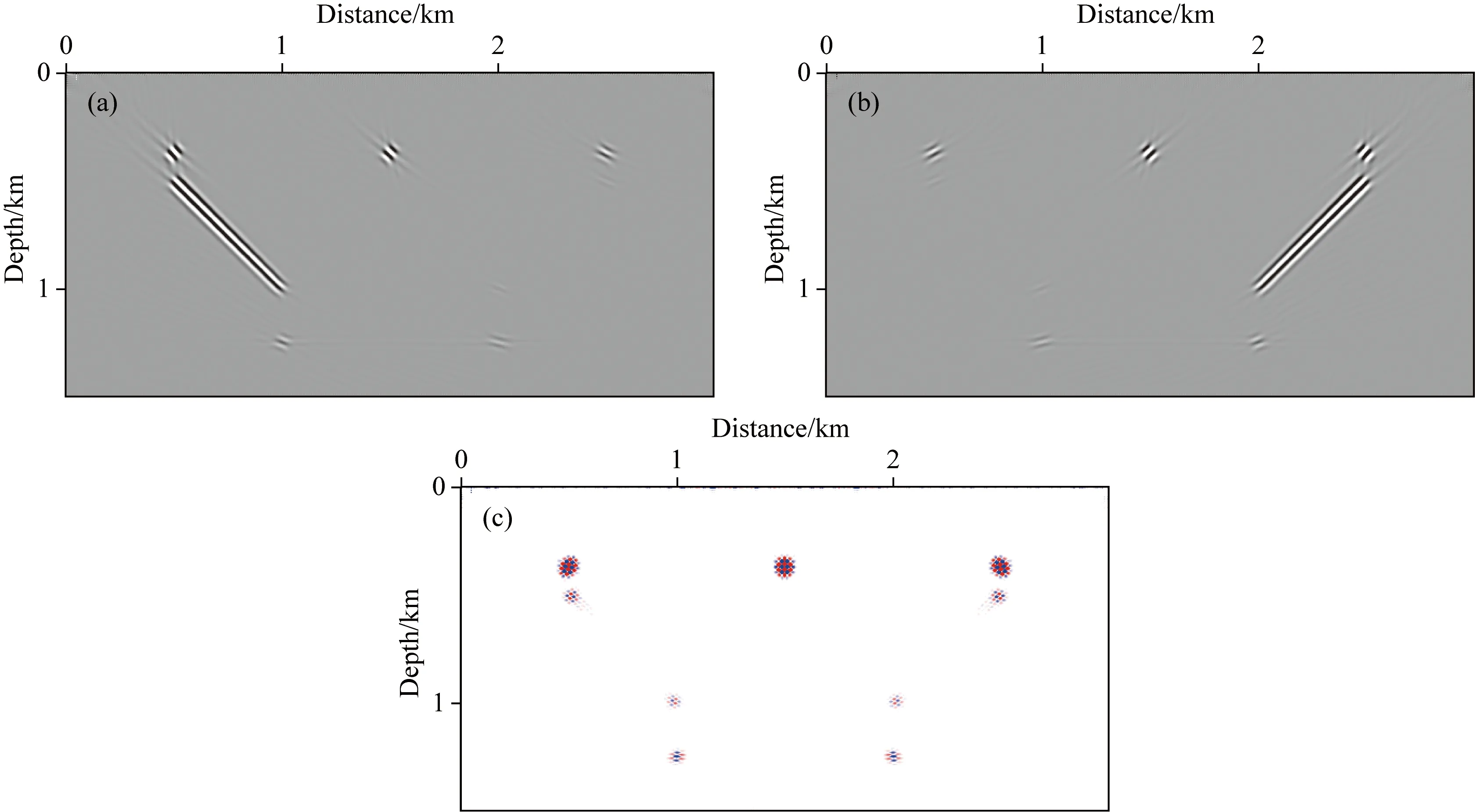
图8 简单模型按照式(11)中的成像条件得到的成像剖面(a)负倾角构造;(b)正倾角构造;(c)绕射点剖面,为(a)和(b)的乘积.Fig.8 Imaging profiles of the simple model according to image conditions in equation (11)(a)The negative-dip structure;(b)The positive-dip structure;(c)The profile of diffraction points,which is the product of (a)and (b).
在计算叠加剖面的同时,我们提取了共成像点倾角道集,并在图9中展示了分别与I1、I2、I3、I4和Isum所对应的角道集在横向1500 m处的片段.从图中可以看出,平界面在以I1和I2为成像条件提取的道集上没有能量聚集,但是绕射点在四种成像条件下均可被呈现.在叠加后的角道集9e上,绕射波能量连续分布在一段区域内,而反射波的能量则聚焦在0°附近.以这些特征为依据,我们在倾角域手动拾取了绕射波能量.图10展示了拾取的结果,绕射点和界面不连续点都得到了很好的呈现,且保留了同相轴的振幅和相位特征.至此,三种绕射点成像方案在简单模型上都得到了良好的效果.

图9 简单模型在不同成像条件下的倾角道集(a),(b),(c)和(d)分别与成像条件 I1,I2,I3和I4对应;(e)是(a),(b),(c)和(d)之和.Fig.9 Dip gathers for the simple model under different imaging conditions(a),(b),(c),and (d)correspond to the imaging conditions I1,I2,I3,and I4,respectively.(e)is the sum of (a),(b),(c),and (d).

图10 简单模型在倾角域手动拾取能量得到的绕射点剖面Fig.10 Diffraction point profile of the simple model obtained by manually picking up energy in the dip-angle domain
2.2 Marmousi2模型
相对复杂的Marmousi2模型的速度变化如图11a所示.该模型在水平方向上有1325个采样点,竖直方向上有467个采样点.震源埋深为5 m,总炮数为40,炮间距设置为165 m.而检波器间隔设为5 m,在整个地表均有分布.地震数据同样由时间二阶、空间八阶的有限差分算法模拟得到.偏移速度由真实模型经过高斯光滑之后得到,如图11b所示.

图11 Marmousi2模型真实速度(a)与偏移所用的背景速度(b)Fig.11 True velocity of the Marmousi2 model (a)and background velocity used for migration (b)
利用震源波场的左下组分和检波器波场的右上组分之间的互相关运算I2,我们得到了如图12a所示的负倾角构造;与之相反,利用震源波场的右下组分和检波器波场的左上组分之间的互相关运算I1,我们得到了如图12b所示的正倾角构造.然后,借助正负倾角剖面的乘积,实现了绕射点和间断点的定位,如图12c所示.同样,我们计算了采用I3和I4成像条件时的结果,即13a和13b,二者具有很好的相似性.

图12 Marmousi2模型的负倾角剖面(a)和正倾角剖面(b),以及最终的绕射点剖面(c)Fig.12 The negative-and positive-dip profiles of the Marmousi2 model,and the final diffraction point profile


图13 Marmousi2模型在成像条件I3(a)和I4(b)下的结果,以及完整的剖面(c)Fig.13 (a)and (b)are the imaging profiles of the Marmousi2 model under imaging conditions I3 and I4,respectively.(c)is the complete profile

图14 Marmousi2模型按照方案三得到的成像剖面(a)负倾角构造;(b)正倾角构造;(c)绕射点剖面,为(a)和(b)的乘积.Fig.14 Imaging profiles of the Marmousi2 model obtained from scheme 3(a)The negative-dip structure;(b)The positive-dip structure;(c)The profile of diffraction points,which is the product of (a)and (b).
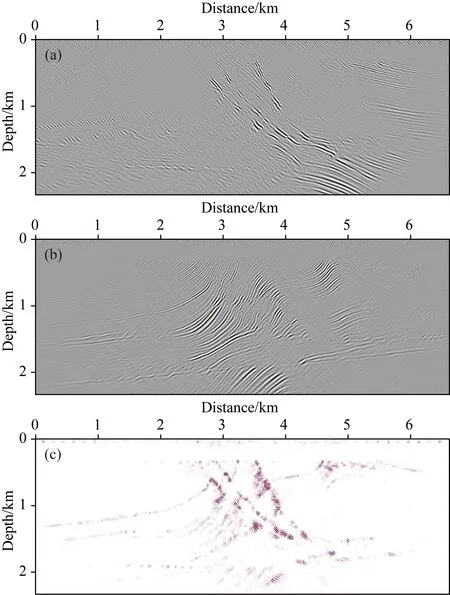
图15 Marmousi2模型按照式(11)中的成像条件得到的成像剖面(a)负倾角构造;(b)正倾角构造;(c)绕射点剖面,为(a)和(b)的乘积.Fig.15 Imaging profiles of the Marmousi2 model according to imaging conditions in equation (11)(a)The negative-dip structure;(b)The positive-dip structure;(c)The profile of diffraction points,which is the product of (a) and (b).
在图16中,我们分别展示了与I1,I2,I3和I4相对应的倾角道集的片段,其位于地表2500 m处.相较于简单模型,Marmmousi2模型提取到的角道集噪音更加发育,绕射点的识别特征也不够强.在此,我们采用中值滤波对绕射波信号进行了甄别和判定,得到了如图17的结果.当绕射点埋深较大且观测系统孔径有限时,绕射波信号与反射波信号并无显著区别,为能量拾取带来了一定的困难.因此,与图12c相比,成像结果除在正确位置附近(如断层处)比较清晰和准确外,在其他区域也有部分能量残余.

图16 Marmousi2模型按照不同成像条件得到的倾角道集(a),(b),(c)和(d)分别与成像条件 I1,I2,I3和I4对应;(e)是(a),(b),(c)和(d)之和.Fig.16 Dip-angle gathers for the Marmousi2 model under different imaging conditions(a),(b),(c),and (d)correspond to the imaging conditions I1,I2,I3,and I4,respectively.(e)is the sum of (a),(b),(c),and (d).
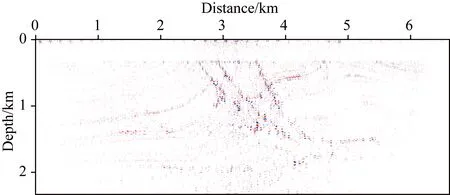
图17 Marmousi2模型在倾角道集通过中值滤波得到的绕射点剖面Fig.17 Diffraction point profile of the Marmousi2 model is obtained by median filtering the dip-angle gathers
3 结论
本文以绕射点为成像目标,分析了基于逆时偏移的各种绕射波成像方案.既利用了逆时偏移方法对地下构造归位准确的优点,又尽量减少计算成本.通过理论分析和数值算例验证,我们将三种方案总结如下:
(1)借助震源波场和检波器波场的不同组分之间的互相关,可以实现不同构造的成像.利用绕射点在正倾角剖面和负倾角剖面均能呈现的特点,通过乘法条件可以实现绕射点的定位.这一方法经过与Hilbert变换和伴随波场延拓相结合,存储成本大大降低,计算效率得以提高;
(2)从Causal成像条件出发,推导正负倾角构造成像公式,从而可以利用空间域的Hilbert变换避免震源波场和检波器波场的方向分解;
(3)Poynting矢量法提取倾角道集进而拾取绕射能量.为了提升角道集的质量,我们采用先波场分离再计算倾角的策略,避免了Poynting矢量在波场重叠区域求取不准的问题.这一方法的运算量和存储量都较大,并且当偏移孔径有限时,绕射波信号和反射波信号之间的区别会被弱化,从而在拾取上造成困难;
(4)通过地震剖面在波数域的分解,实现正负构造剖面的提取.然后采取乘法运算,确定绕射点和间断点的位置.其中,为了避免在比较平缓或接近垂直界面上的错误成像,我们牺牲少许绕射点信息,将波数分量接近于0的区域值设置为0.相较于前两种方案,这种图像处理的方法具有以下优点:运算和存储成本极低,不受偏移方法的限制,针对大工区可以只对目标区域做局部化成像.当然,本方法也需要信噪比较高的剖面作为输入.
附录A
由正文可知

(A1)
在频率-波数域,上式可表示为

(A2)
因为
(A3)
在此,我们定义中间变量
(A4)
显然,有
(A5)
同理,有
(A6)
(A7)

(A8)
将上式变换回空间-时间域,可得
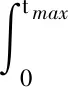
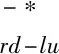
(A9)
其中,
(A10)
上标“±”表示取“+”或者取“-”.显然,我们可以通过对空间进行Hilbert变换实现式(A9),即
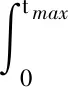
(A11)
其中,H算子定义为Hx(s)=s+iHx(s),Hz(s)=s+iHz(s),Re{·}表示取实数部运算.
与上述推导类似,我们得出
(A12)
这与Zhang等(2020)的结论一致.
