基于深度学习的接收函数横波速度预测

杨庭威，曹丹平*，杜南樵，崔荣昂，南方舟，徐亚，梁策

1 中国石油大学(华东)，地球科学与技术学院，青岛 266580 2 中国科学院地质与地球物理研究所，中国科学院油气资源研究重点实验室，北京 100029 3 中国科学院大学，北京 100049 4 中国科学院地球科学研究院，北京 100029

0 引言

自Phinney(1964)提出接收函数的基本概念以来，接收函数方法便成为研究地球内部圈层间断面、速度结构的重要方法之一(Phinney,1964;Ammon et al.,1990;Leahy et al.,2012;Shibutani et al.,1996;Zhu and Kanamori,2000).Langston(1977)通过对径向分量和垂直分量的谱分解(反褶积)，从远震事件的长周期体波中提取了接收函数(Langston,1977).Owens等(1984)将接收函数的方法扩展到宽频，并利用远震P波接收函数的波形拟合方法来反演地壳速度，发展了基于远震接收函数的线性化反演方法(Owens et al.,1984).尽管线性化方法在某些情况下得到的地壳模型可以很好地拟合观测到的接收函数波形，但结果通常对初始模型有很强的依赖性，常常收敛到局部最优解而非全局最优解(Sambridge,1999a；任骏声和沈旭章，2015).相比之下，基于马尔科夫链的蒙特卡罗方法可以避免局部极小值，逼近全局最优解(Sambridge,1999b;Vinnik et al.,2004;Zheng et al.,2005).但该方法需要通过大量的正演计算来采样反问题的后验概率密度分布，使其在实际应用中受到了一定限制.

线性化反演方法和蒙特卡罗方法都是模型驱动的，远震接收函数反演的数据量较大，每次迭代都需要进行大量正演计算.而利用深度学习从大量的远震接收函数数据中自动提取其复杂的特征，预测台站下方横波速度，避免全局反演解的不稳定性，并克服传统方法中拟合接收函数迭代运算的大运算量缺陷，大幅提升了反演的速度、精度和效率.其中卷积神经网络通过共享权重，设置相对较少的参数即可构建层数更深的网络，其提取特征的能力较以往的人工神经网络有很大提升(刘帅师等,2016;Krizhevsky et al.,2017;安鹏和曹丹平,2018;Puzyrev,2019;Zhu and Beroza,2019)，非常适用于地震波识别与定位以及接收函数反演等这类特征提取与参数优化的问题(Van der Baan and Jutten,2000;Kong et al.,2016;Ross et al.,2018；段刚，2021).在反演中只需将径向接收函数作为输入参数，经过卷积层、下采样层和全连接层的前向传播和反向传播，网络训练结束后便能直接得到横波速度，这对于反演岩石圈速度从模型驱动、方程反演朝着自动化、智能化方向发展具有十分重要的意义.

本文基于卷积神经网络，设计了利用接收函数预测横波速度的方法.在研究中利用全球模型参数的合成接收函数与高质量台站观测接收函数，建立一个与全球地壳结构复杂程度高度一致的样本库集合，提高卷积神经网络的泛化能力.最后，我们将训练好的神经网络应用到被动源海底地震仪观测数据上，对琉球海沟地区的地壳结构进行深入研究.

1 卷积神经网络预测方法

基于卷积神经网络对接收函数波形进行训练并预测地下横向波速特征，其核心是构建合理的网络结构，建立具备泛化能力的样本集进行测试.本文引入U-net的核心结构，其跳层的连接可以减少神经网络中梯度爆炸或者消失的问题，并且U-net中多层次的特征信息可以从不同尺度挖掘接收函数和横波速度之间的关系，因而选用U-net提取接收函数复杂的特征，预测台站下方横波速度.

基于U-net卷积神经网络结构的基本技术框架如图1所示，将远震P波径向接收函数的波形作为输入参数，对应的横波速度结构作为样本标签.左图每个绿色盒对应一个多通道特征图.通道的数量显示在盒子的顶部.黄色盒代表复制的特征图.不同颜色箭头表示不同的操作.最先提出的U-net是用于医学领域的细胞分割(Ronneberger et al.,2015)，输入输出均为二维数据，为了适应地震反演的实际问题，我们将U-net拓展为一维.可以更好适用于转换输入数据和输出数据的维度，例如输入数据是不同震中距的多道接收函数为二维数据,而输出数据是台站下方一维的横波速度结构为一维数据.

图1 基于U-Net的卷积神经网络结构Fig.1 Architecture of U-Net-based convolutional neural network

为提高该网络结构的特征提取能力，本文在U-net网络上进行局部改进，将最后卷积层的输出经过Flatten操作后传入全连接层.加深了神经网络的深度，也就使深层的神经元可识别更为抽象的信息，同时利用dropout操作让某神经元的激活值以一定的概率p停止工作，防止过拟合，使模型泛化性更强.从而将反演问题简单化，精确化.

1.1 卷积神经网络的前向传播

池化层的前向传播过程是以卷积层提取的特征作为输入传到下采样层，并在下采样层进行池化操作，降低数据的维度，避免过拟合.网络采用的池化方法为均值池化，表示取局部接受域中的平均值.

卷积神经网络前向传播公式为：

x=f(u)，

(1)

u=W*x+b，

(2)

1.2 卷积神经网络的反向传播

本文用来衡量真实标签值与预测结果之间误差情况的目标函数为：

(3)

其中f(ul(w,b)为网络最后一层的输出，V为标签，w和b分别是权值和偏置，在Adam算法中统一用θ来表示.

本文利用Adam算法更新网络权值(Kingma and Ba,2017)，具体过程如下:

(1)设置参数.步长ε设为0.001;矩估计的指数衰减速率ρ1和ρ2在区间[0,1)内(默认设为0.9和0.999);用于数值稳定的常数δ(默认设为10-8)；

(2)初始化参数.初始化一阶和二阶矩变量s=0，r=0;

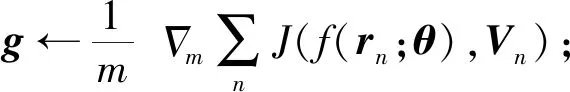
2 接收函数预测横波速度的样本库构建

样本库是深度学习的核心基础，构建高质量的样本库是提高深度学习泛化能力的基础和关键，本文从合成接收函数样本及实际数据的接收函数样本两方面出发提出构建样本训练集的优化方案，建立与全球地壳结构复杂程度高度一致的样本库集合.

2.1 合成接收函数样本

本文采用一维水平层状各向同性介质的反射率方法合成理论地震波形，该技术可以用较少的耗时合成与实际数据较为接近的地震波形，再使用最大熵反褶积法从三分量波形数据中提取接收函数(Levin and Park,1997a,b;Li et al.,2010).最大熵谱反褶积是以熵极大作为互相关函数和自相关函数的外推准则，来求取接收函数.该方法在外推计算过程中，其反射系数总是小于1，以确保最大熵反褶积的稳定性，并对数据时窗外的数据做更加合理的假设，以获得高分辨率的接收函数(吴庆举等,2003).同一模型的合成数据包括20道径向接收函数，以此模拟不同地震事件.正演计算采用2.5的高斯系数，在P到达之后使用32 s的时间窗，从而保证接收函数包含直达波和主要转换波的信息.

为提高网络的泛化能力，建立一个与全球地壳结构复杂程度高度一致的样本库.为此我们基于Crust1.0模型进行合成接收函数样本的构建工作.在Crust1.0全球模型中每隔5经纬度取一个点，共2592个模型数据，不同深度的横波速度分布如图2所示.并将介质中的每一层细分为1 km厚的区间，用随机高斯噪声扰动每一薄层的横波速度，扰动均值为0，标准差为0.1 km·s-1，利用所得结果正演射线参数分布在0.042～0.080 s·km-1内的20道接收函数(该范围内接收函数质量较好)，再添加随机噪声，使其与真实接收函数更为接近.

全球地壳各处厚度不一，大陆部分平均厚度为37 km；而海洋部分平均厚度则只有约7 km.高山、高原部分地壳最厚可达70 km；裂谷、海沟部分地壳最薄低至1.5 km.样本中包含了从1.5 km到70 km厚度的地壳模型.样本集的地壳厚度分布如图2g所示，其中地壳厚度大于60 km或小于3 km样本不足，因此本文只讨论地壳厚度为5～50 km范围内时该方法的有效性.将地壳模型进行编号，用随机数字生成器随机选取地壳速度模型，与低速体模型、高速体模型、高低混合模型随机组合形成408个复杂模型.基于模型参数正演射线参数分布在0.042～0.080 s·km-1内的20道接收函数，并添加随机噪声(图3).

图2 地壳横波速度结构的水平切片(a)5 km;(b)10 km;(c)15 km;(d)25 km;(e)35 km;(f)45 km；(g)地壳模型分布(数据集来源于Crust1.0).Fig.2 Horizontal slices of crustal shear wave velocity structures at depths(a)5 km;(b)10 km;(c)15 km;(d)25 km;(e)35 km;(f)45 km；(g)Crustal model distribution (dataset from Crust1.0).

图3 合成接收函数样本展示(a)低速体模型;(b)合成接收函数;(c)添加随机噪声的接收函数.Fig.3 Sample set of synthetic receiver functions(a)Low-speed model;(b)Synthetic receiver functions;(c)Synthetic receiver functions with random noise.

2.2 观测接收函数样本

除合成接收函数样本外，本文进一步基于高质量的实际地震观测数据进行接收函数提取，并将其作为样本集的组成之一进行训练.在JAMSTEC网站上申请了2013年11月23日到2014年2月18日琉球海沟附近30个OBS海底地震仪的连续波形数据.为此对实际地震数据先进行预处理，包括格式转换和地震识别.首先是把原始记录SEED格式数据转换成较为通用的SAC格式，然后根据哈佛大学的CMT目录截取地震震级在5.5级以上，震中距在30°～90°的三分量地震波形;陆地地震数据方面，在IRIS网站申请美国地区10个固定台震级在5.5级以上，震中距在 30°～90°的三分量地震波形数据.

从远震波形中提取出射线参数在0.042～0.080 s·km-1范围内的接收函数.每个台站分别挑选出20道质量较高的接收函数，进行可逆跳跃马尔可夫链蒙特卡罗接收函数反演台站下方的横波速度结构,作为网络的标签(图4).样本集兼顾了陆地和海洋不同的地震数据，以提高网络对不同类型观测接收函数数据进行横波速度预测的泛化能力.

图4 观测接收函数样本展示(a)、(c)可逆跳跃马尔可夫链蒙特卡罗接收函数反演的横波速度;(b)、(d)观测接收函数.Fig.4 Sample set of observed receiver functions(a)and (c)Shear wave velocities inverted by a reversible jumping Markov chain Monte Carlo；(b)and (d)Observed receiver functions.

3 方法测试与实验

3.1 输入样本的选取

随着Crust系列全球地壳模型精度的不断提高，当前最为详细，分辨率最高的全球地壳模型是Crust1.0地壳模型，其地形特征的多样性和完整性非常适用于作为神经网络的训练集.同时，在全球模型数据的基础上，本研究加入了随机生成的陆壳高原、洋壳沉积层以及高低速异常体等复杂模型以及实际的观测数据，以提高训练数据集的多样性，增强模型的泛化能力.因此，将全球模型中2592个合成数据、308个复杂模型的合成数据以及16个观测数据(包括陆地台站8个，OBS数据8个)，共计2916个样本作为网络的训练数据集.剩下100个复杂模型的合成数据以及4个观测数据，共计104个样本作为网络的测试数据集，用于评估最终模型的泛化能力.

3.2 测试集数据检验

对网络进行3万次训练学习，耗时方面，利用NVIDIA 2080 GPU训练耗时只有10 h，这很大程度上由计算机硬件配置、学习系数的数据量所决定.用训练好的网络模型进行横波速度预测，在i5四核CPU上预测横波速度耗时仅在5 s左右.在测试集中计算四个具有代表性的模型：洋壳模型、高原模型、高速模型和低速模型来验证方法的有效性及准确性.

图5为随机选取测试集中四个代表性模型的预测结果，可见四个结果预测横波速度均与模型真实值基本一致.图5a为洋壳模型的预测结果，黑色实线表示模型的真实横波速度随深度变化的曲线，红色虚线表示利用网络预测的横波速度随深度变化的曲线，可见对5 km沉积层厚度以及12 km的Moho面深度符合较好，预测误差不超过0.2%.图5b为陆地高原模型的预测结果，对3 km沉积层厚度以及40 km的Moho面深度符合较好，预测误差不超过0.6%.图5c为高速体模型的预测结果，在17 km处存在8.5 km高速体厚度，以及41 km的Moho面深度符合较好，预测误差不超过0.5%.图5d为低速体模型的预测结果，在8 km处存在9 km高速体厚度，以及42 km的Moho面深度符合较好，预测误差不超过0.4%.预测结果均具有很好的符合度.

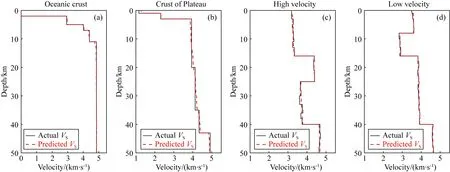
图5 测试集中合成接收函数预测的横波速度结果(a)洋壳模型的预测结果;(b)陆地高原模型的预测结果;(c)高速体模型的预测结果;(d)低速体模型的预测结果.Fig.5 Shear wave velocity models predicted by synthetic receiver functions in test dataset(a)Oceanic crust model；(b)Plateau model；(c)High-speed model；(d)Low-speed model.

为更好地检验网络的泛化性，在测试集中加入地壳厚度为1～70 km的70个不同样本如图6a所示，并计算预测结果与模型均方误差随地壳厚度分布变化，以用于评估网络的可靠性.图6c测试结果显示：在地壳厚度为5～60 km范围内预测误差较小，而该范围内地壳厚度已基本能覆盖实际观测台站下方的地壳厚度.由于训练集中鲜有地壳厚度小于5 km大于60 km的样本，因此该范围内地壳厚度预测误差较大.除此之外，在测试集中再加入横波速度为0.5～3.5 km·s-1的300个不同的速度异常体样本如图6b所示，其预测结果与模型均方误差随异常体速度分布如图6d所示：当低速异常值大于1 km·s-1时预测误差较小，表明网络在预测低速异常幅值不低于1 km·s-1时仍具有较高分辨率.

图6 测试集中合成接收函数预测结果评估(a)地壳厚度为1～70 km模型；(b)异常体横波速度为0.5～3.5 km·s-1模型；(c)预测结果与模型均方误差随地壳厚度分布；(d)预测结果与模型均方误差随异常体速度分布.Fig.6 Evaluation of synthetic receiver functions in test dataset(a)Models with crustal thickness 1～70 km；(b)Abnormal body of shear wave velocity as 0.5～3.5 km·s-1；(c)MSE of prediction versus crustal thickness；(d)MSE of prediction versus velocity of anomalous body.

训练集中单个模型的20道不同的合成接收函数其射线参数是等间隔分布在0.042～0.080 s·km-1范围内如图7a所示，旨在利用神经网络学习到不同震中距的接收函数的平均特征来预测台站下方的横波速度结构.而实际观测到的单台接收函数的震中距是随机分布的，特别是流动观测数据很难得到震中距规则分布的接收函数.因此在测试集中加入射线参数随机分布在0.042～0.080 s·km-1内的20道含噪接收函数如图7b所示.同时，为检验模型的稳健性，在测试集中加入1000个射线参数随机分布的含噪接收函数样本，预测结果与模型均方误差如图7d所示，可以看出其误差均在允许范围内.

图7 测试集中射线参数随机分布的合成接收函数预测结果评估(a)射线参数规则分布的合成接收函数；(b)射线参数随机分布的合成接收函数;(c)射线参数规则分布的合成接收函数与射线参数随机分布的合成接收函数预测结果；(d)随机分布的接收函数样本预测误差分布.Fig.7 Evaluation of synthetic receiver functions with random distribution of ray parameters in test dataset(a)Synthetic receiver functions with regular distribution of ray parameters;(b)Synthetic receiver functions with random distribution of ray parameters;(c)Prediction results of synthetic receiver functions with regular distribution of ray parameters and synthetic receiver functions with random distribution of ray parameters;(d)MSE of prediction versus test dataset number.

进一步对实际数据进行测试，随机选取测试集中OBS观测接收函数样本以及陆地台站观测接收函数样本来检验网络在预测横波速度的泛化能力.

图8为随机选取测试集中海底地震仪和陆地地震台站两种观测类型的接收函数样本的预测结果;可见两种观测接收函数预测的横波速度结果均与可逆跳跃马尔可夫链蒙特卡罗接收函数反演的横波速度基本一致，横波速度间断面所反映的莫霍面深度与H-κ叠加结果也较为一致.

图8 测试集中观测接收函数预测的横波速度结果(a)OBS观测接收函数预测的横波速度结果；(b)OBS观测接收函数的H-κ叠加结果;(c)陆地台观测接收函数预测的横波速度结果；(d)陆地台观测接收函数的H-κ叠加结果.Fig.8 Shear wave velocity predicted by observed receiver functions in test set(a)By the receiver function observed on the OBS；(b)Result of H-κ stacking for receiver function observed on the OBS；(c)Shear wave velocity predicted by the receiver function observed on land station；(d)Result of H-κ for the receiver function observed on the land station.

当仅用实际样本训练的网络时，网络学习到的特征只能针对此研究区域的横波速度预测，且由于实际样本较少容易出现过拟合现象.如图9所示，预测的横波速度与实际横波速度点距离回归线较远，观测数据与合成数据预测结果均不太理想.当仅利用Crust1.0模型的合成数据训练网络时，网络能较好预测合成数据和实际数据的横波速度，相较于仅用实际训练的预测精度有所提升.如图10所示，预测横波速度与实际横波速度点相对集中于回归线中，其中合成数据预测结果有明显的提升.当样本集中同时包括合成数据和实际数据训练网络时，网络能学习到Crsut1.0中更丰富的模型特征，同时加入少量的实际数据训练，能使网络更适用于实际数据的预测，增强网络的泛化能力.如图11所示，预测横波速度与实际横波速度点基本落在回归线上，实际数据与合成数据的预测精度均有所提升.

图9 训练集中仅有实际数据网络预测的横波速度与实际横波速度统计(a)OBS观测数据预测的横波速度与实际横波速度相关性；(b)合成数据预测的横波速度与实际横波速度相关性.Fig.9 Statistics of predicted shear wave velocities and actual shear wave velocity from trained set only with observed samples(a)Correlation between shear wave velocities predicted by OBS observational data and actual shear wave velocities；(b)Correlation between shear wave velocities predicted by synthetic data and actual shear wave velocities.

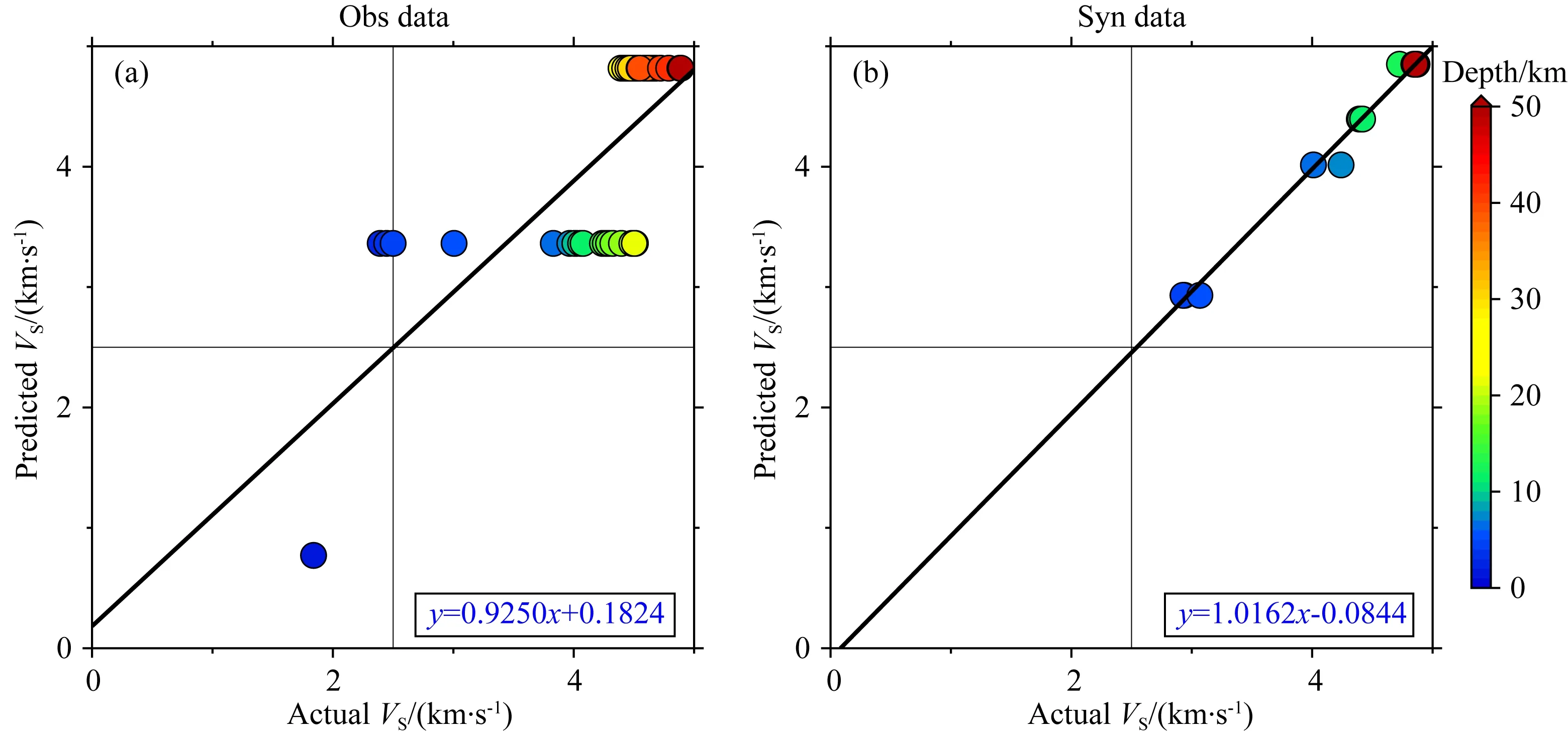
图10 训练集中仅有合成数据网络训练预测的横波速度与实际横波速度统计(a)OBS观测数据预测的横波速度与实际横波速度相关性；(b)合成数据预测的横波速度与实际横波速度相关性.Fig.10 Predicted shear wave velocity and actual shear wave velocity statistics trained only with synthetic samples(a)Correlation between shear wave velocities predicted by OBS observation data and actual shear wave velocities;(b)Correlation between shear wave velocities predicted by synthetic data and actual shear wave velocities.

图11 训练集中有实际数据及合成数据网络预测的横波速度与实际横波速度统计(a)OBS观测数据预测的横波速度与实际横波速度相关性；(b)合成数据预测的横波速度与实际横波速度相关性.Fig.11 Statistics of predicted shear wave velocity and actual shear wave velocity from trained data set with observed samples and synthetic samples(a)Correlation between shear wave velocities predicted by OBS observational data and actual shear wave velocities；(b)Correlation between shear wave velocities predicted by synthetic data and actual shear wave velocities.

上述结果表明，基于全球模型数据以及部分质量较高的观测接收函数建立样本库能有效提高网络的泛化性，同时对比接收函数H-κ叠加结果验证了利用卷积神经网络预测的横波速度间断面具有较高的可靠性.

4 实际数据应用

海洋地壳结构研究能提供大洋内部结构的认识，基于海底地震仪的观测应用为获得海洋地壳结构提供了良好的数据基础.特别是近年来被动源OBS观测阵列的布设为接收函数研究提供了良好的数据支撑，其研究成果可为研究精细海洋地壳结构、海底扩张和板块运动提供重要的地球物理依据(Akuhara et al.,2016;Audet,2016;郭衍龙等,2016;Liu et al.,2020).因此，本文选取琉球海沟地区作为研究区进行实际应用检验，设计利用卷积神经网络识别被动源接收函数的波形特征来预测琉球海沟附近台站下方横波速度结构，并通过速度间断面进一步获取研究区域的莫霍面深度.

为验证基于卷积神经网络的接收函数横波速度预测方法对地壳结构求取的准确性和可靠性，利用在JAMSTEC网站上申请的30个OBS台站数据进行海底地壳结构的研究.琉球海沟是菲律宾海板块向下俯冲到欧亚板块的一个俯冲带构造，具有强烈的构造活动，是研究太平洋西岸汇聚型板块边界的重要研究区域(Ali and Hall,1995;Hall et al.,1995;Sdrolias et al.,2004;Yumul et al.,2009;Arai et al.,2016).图12中红色线表示板块的边界，黑色线为断层，白色箭头表示板块俯冲的方向，被动源OBS台站所处位置由北向南从琉球岛弧过渡到琉球海沟南部的斜坡带处.由于3台OBS数据无法获取，本文仅选取研究区域27个数据质量较高的OBS，并提取20道接收函数作为输入参数，经过训练好的卷积神经网络输出横波速度，并求取横波速度在深度方向的梯度，从中获得研究区域OBS下方莫霍面深度.

图12 琉球海沟OBS地理位置Fig.12 Geographical locations of OBS in the Ryukyu Trench

为验证卷积神经网络结果的可靠性，结合接收函数H-κ叠加结果与Crust1.0模型进行对比，如图13所示.图14为利用卷积神经网络预测研究区海域的横波速度所计算的莫霍面深度分布图，呈现出由北向南莫霍面深度从26 km到12 km逐渐减小的趋势，以及地壳厚度的北厚南薄趋势，明显地分为三级阶梯，与接收函数H-κ叠加结果以及Crust1.0莫霍面深度分布基本一致.通过对比，验证了利用卷积神经网络预测的横波速度间断面具有较高的可靠性.由于具有更高的分辨率，利用卷积神经网络得到莫霍面深度分布能够更为细致地刻画研究区的地壳结构变化，同时满足了准确度，精细度.

图13 研究区域莫霍面深度分布(a)H-κ叠加结果莫霍面深度分布；(b)Crust1.0莫霍面深度分布图.Fig.13 Moho depth distribution in the study area(a)Moho depth distribution for H-κ stacking；(b)Map showing Crust1.0 Moho depth distribution.

图14 基于卷积神经网络预测的横波速度所计算的莫霍面深度分布图Fig.14 Moho depth distribution based on the shear wave velocity predicted by convolutional neural network

5 结论

基于卷积神经网络方法本文设计了一种接收函数横波速度的预测方法，利用深度学习从大量的远震接收函数数据中自动提取其复杂的特征，预测台站下方横波速度，避免全局反演解的不稳定性，并克服传统方法中拟合接收函数迭代运算的大运算量缺陷，大幅提升了反演的速度、精度和效率.本研究基于Crust1.0模型构建模型接收函数样本，基于陆地及海底地震高质量观测实际数据构建实际接收函数样本，建立与全球地壳结构复杂程度高度一致的样本库集合，增强了网络学习的泛化能力.经过测试集对模型及实际数据的检验均取得了良好的横波速度预测效果.进一步将该方法用于琉球海沟地区被动源海底地震数据接收函数研究，获得了该地区海洋地壳结构特征，结果表明该地壳莫霍面在12～26 km范围内变化，整体莫霍面特征较Crust1.0模型更为精细，为认识琉球海沟地区深部结构提供了可靠参考.

致谢感谢审稿专家提出的宝贵意见.IRIS、Japan Agency for Marine-Earth Science and Technology为本研究提供地震数据.