基于数字图像的真实细观非均质岩土力学分析数值方法

岳中琦

香港大学土木工程系，香港

0 引言

0.1 岩土细观非均质现象与特性

岩石是由各种矿物颗粒镶嵌和胶结组成的固体物质，岩体是岩石和包括节理及裂隙在内的各种不连续面自然组成的固体物质.细观非均质物质和不连续面的空间分布是岩石和岩体的基本物理力学性质.土体主要由黏土、粉土、砂土和砾石按照不同颗粒级配、经历各种地表风化或沉积作用形成的.细观不均质是土体的基本特性.混凝土是建造高坝、公路、桥梁和楼宇等建筑的主要人造固体材料，也是最典型的细观非均质材料.

岩土和混凝土材料的变形和破坏往往造成人员伤亡、经济损失和工程安全问题.精准进行岩土力学数值计算和分析是岩土破坏机理研究、灾害事件判识预测、变形破坏防治设计与施工等工作的基础性科学问题，相关科学方法的突破将会从根本上提升灾害机理认识和减灾工作的水平.

0.2 传统方法与存在问题

岩土力学研究、计算和预测岩石、岩体、土体和混凝土材料在载荷作用下的弹性变形、塑性变形(或脆性破裂)和破坏的响应过程，在岩土工程各个理论和应用领域起关键和核心作用.长期以来，在应用经典连续介质力学理论和方法基础上，岩土力学在岩土本构关系和数值力学计算方法方面取得了极大的发展和进步.

但是，几乎所有岩土力学研究均采用岩土材料物理和力学性质在空间上是均匀分布、分片均匀分布、或人为给定统计不均匀分布的基本假设.根据公开的文献，大约在2002年前的岩土力学数值计算方法论文均没有真实定量地考虑由多种不同矿物、砂石、孔隙等组成的，具有不同物理力学性质的真实细观非均质材料的空间分布.

图1给出了传统岩土力学主流分析方法和流程.它是多年来众多岩土工作者在大量的室内试验、理论分析、数值计算和工程经验基础上建立的，经过检验和验证，得到了广泛应用.

图1 岩土力学主流分析方法的流程图(岳中琦,2006)Fig.1 Flow chart of dominant methods in geomechanics (Yue,2006)

建立岩土和混凝土材料本构关系和参数过程的室内力学试验，一般都是对200 mm左右的小型规整试件进行测试.在测得同类试件数据后，再对这些数据进行统计或平均等合理优化.但是，小尺寸试件在细观上仍然是由很多种物理和力学性质不同的介质组成，试验所测结果是试件在外载荷作用下的总体响应与表现.不同介质及其细观分布能够影响试件内部各点实际物理场、力学场及其总体物理力学响应.然而，这些影响在传统岩土力学主流分析方法中缺乏定量计算和分析.传统岩土力学主流分析方法使用了均质化本构模型，导致它们难以真实体现和精准预测细观非均质材料的力学响应、特别是破坏过程响应.

0.3 沥青混凝土材料细观非均质结构有限元分析实例

如图2所示，Sepehr等(1994)进行了考虑沥青混凝土道面材料细观非均质结构的有限单元力学数值分析.图2a是常规沥青混凝土道路结构与车轮载荷力学计算与分析模型.图2b 揭示了所建立的100 mm厚薄层道面(AC)的骨料和基质细观有限单元网格.骨料由大颗粒砂石组成，基质由细砂与沥青胶结物组成.从图2b可见，这种人为细观非均质材料分布和有限单元网格是相当简单、且有手工人为的影响.

图2 考虑沥青混凝土(AC)道面材料细观非均质结构的有限单元力学模型(Sepehr et al.,1994)(a)道面结构；(b)沥青混凝土道面骨料和基质的有限元网格.Fig.2 Finite element mechanical model of road pavement structure with meso-heterogeneous asphalt concrete (AC)surface seam (Sepehr et al.,1994)(a)Pavement structure model;(b)Finite element mesh of aggregates and matrices in AC surface seam.

令人关注的是，这种细观非均质有限元数值分析结果揭示了沥青混凝土道面薄层内部底部存在较大水平拉张应力.这个非均质计算结果与用均质沥青混凝土道面薄层模型计算得到的结果不一样.

1 基于数字图像处理技术的细观非均质测量与计算

1.1 沥青混凝土材料细观非均质结构的数字图像测量

在1990年代初期，数字图像处理技术在国际上刚刚兴起(Yue and Morin,1996).如图3所示，数字图像处理技术可以定量研究沥青混凝土细观骨料的空间分布.图3a是一幅沥青混凝土试样横截面照片.图3b是对应的骨料与基质定量空间分布图.

图3 直径150 mm的沥青混凝土材料细观非均质结构(Yue and Morin,1996)(a)真实照片；(b)基质和骨料黑白分布.Fig.3 Cross-section of meso-heterogeneous asphalt concrete with 150 mm diameter (Yue and Morin,1996)(a)Actual digital image;(b)Black and white digital image of matrix and aggregates.

Yue等(1995)、Yue和Morin(1996)论证了骨料及其细观空间分布对沥青混凝土结构稳定性和力学强度所起的决定作用，并指出了数字图像技术与岩土力学数值方法的结合将是一项有前途和生命力的研究课题和方向.这一论证得到了Ghaly(1997)、Kuo和Freeman (1998)、以及汪海年和郝培文(2008)的认同或发展.

1.2 真实细观骨料非均质岩土和混凝土数值力学计算

早期运用数字图像开展的真实细观骨料非均质分布的岩土和混凝土力学数值计算研究可参见Chen et al.(2004a,b,2005,2006,2007,2013)，Yue et al.(2002,2003a,2003b,2004)和Yue(2006a,b,2007,2008).这些研究建立了一套真实细观非均质岩土材料力学响应的数值求解与分析方法体系，提出了一套将真实细观非均质岩土材料平面图像精准转化为二维和三维数值网格的计算方法，以及确定了考虑真实细观非均质岩土材料在多种经典载荷作用下力学响应的重要规律.上述工作得到了进一步发展与应用，相关文献参见Azari等(2005),Borja和Andrade(2006),Chen等(2004a,b,2005,2006,2007,2013)，Corthésy和Leite(2008),Dyskin等(2018),Fritzen和Böhlke(2011),Zhu等(2006),Li和Wong(2013),Mahabadi 等(2012,2014),Meng等(2018),Molladavoodi和Rahimirezaei(2018),Sun等(2014),Ündül等(2015),Xiong等(2021)，盛金昌等(2006)，徐文杰等(2008),于庆磊等(2006,2010)和张连卫等(2008).以下具体介绍真实非均质岩土力学数值分析方法的三个内容.

2 真实非均质数值分析方法体系

2.1 方法体系的创新

在运用了现代数字图像技术手段的基础上，Yue 等(2003a)建立了一套真实细观非均质岩土材料力学响应的数值求解与分析方法，解决了过去数值计算无法精准真实考虑试件细观非均质分布的难题(Sepehr et al.,1994)，论证了数字图像本身是物体细观介质结构和空间分布的一种精确测量和数字表述的方法.

如图4所示，数字图像技术是通过照相等技术将真实物体用对应的数字图像来表示，并将图像以数字形式储存在计算机中.当物体转换为图像时，其表面或内部不同介质可以通过灰色度或色度的变化在图像中得到准确重现.数字图像是由一个个完全独立的像素点组成的.每个像素点是一根横向扫描线条和一根纵向扫描线条的交汇区域，这些横纵扫描线条均有相同的宽度.因此，每个像素点完全占有一个确定的正方形面积区域.图5和图6是基于图4的进一步数值化处理结果，实际长度和宽度分别均为29.21 mm 和15.68 mm.

图4 长29.21 mm、宽15.68 mm的沥青混凝土黑白数字图像与正方形分片连续函数的关系和特征(a)原始图像(Yue et al.,2003a)；(b)横向扫描线像素点灰度值分布(岳中琦,2006).Fig.4 Relationship and features of black and white digital image for asphalt concrete with 29.21 mm in length and 15.68 mm in width(a)Original image (Yue et al.,2003a);(b)The square discrete function along a line (Yue,2006).

图5 区域分割法自动识别和区分颗粒骨料和周边微细介质(Yue et al.,2003a)(a)初步自动识别结果；(b)细化识别结果.Fig.5 Region segmentation method for automatic recognition and differentiation of particle skeletons and their surrounding fine particles (Yue et al.,2003a)(a)Initial automatic recognition result;(b)Refined recognition result.

图6 标量数据经矢量转化后再自动生成的数值计算网格(Yue et al.,2003a)(a)骨料与基质界线矢量图；(b)自动三角型单元网格划分结果.Fig.6 Finite element mesh automatically generated from the vectorized geometry (Yue et al.,2003a)(a)Vectorized interface lines between aggregates and matrix;(b)Automatically generated triangular finite element mesh.

同一幅数字图像中的每个正方形面积区域大小相同.每个像素点有一个整数值来代表该像素点的灰色度，变化范围为0到255.数字图像方形像素点阵形成了平面上分片连续整数函数.类似地，彩色数字图像的方形像素点阵含有三个不同色度的整数值，形成了三个二维满矩形区域分片连续整数函数.因此，数字图像精确地反映了物体中不同介质种类的空间分布.

2.2 方法体系的四个基本假设

这套可精准考虑细观材料各种介质实际空间分布的力学计算和预测方法有以下四个基本假设.第一，传统岩土力学分析方法和理论能够分析宏观场地岩土体在外载荷作用下响应，既适用于计算分片或分块均匀不同类宏观岩土体的初边值力学问题，也适用于计算分片或分块均匀的不同种细观岩土介质体的初边值力学问题.第二，各类岩土和混凝土材料在细观上由两种或两种以上的不同介质按自然规律组成，同种或不同种介质空间非均匀分布.第三，每一种细观介质(如水、孔隙、石英等单晶矿物)可以被认为是均匀的、有较为确定和稳定的力学本构关系和相关参数.第四，每两种介质之间的接触可以是完全连续或不完全连续的.

2.3 方法体系的四步途径

实现这套方法有以下四步途径.首先，将细观岩土材料各种介质的实际空间分布和尺寸用数字图像表示.第二，根据岩土材料剖面定量区分几种主要组成介质，并获得它们用数字图像表示的确定空间分布.第三，用特定软件打开数字图像文件，运用矢量转换技术，将确定的图像细观介质空间分布转化为矢量细观介质空间分布.第四，矢量细观介质空间分布直接输入现有(包括有限单元法或有限差分法在内)的力学数值计算方法，利用现有软件程序，快速实现相关边初值问题的细观力学数值分析.

3 真实非均质岩土材料图像转化为数值网格

3.1 岩土数字图像信息空间分布确定

每一幅岩土数字图像含有众多材料信息.根据研究目的，将主要的相关信息和数据区分和确定出来，至少可用两种方法自动完成这项任务.其一是边缘检测法：通过寻找出不同介质的内外边界、从而达到确定空间分布的目的.其二是区域分割法：通过寻找具有相同属性的像素点灰或色度值大小分布区域，从而达到区分不同种介质的目的(图5).

3.2 第一种二维网格生成方法

在确定不同介质边界后，可用两种数字图像矢量化网格的自动生成方法.第一种方法如图6所示.该方法使用边缘检测算法自动提取不同介质内边界像素点，采用矢量转换方法将这些内边界像素点转化为由封闭多边形组成的矢量空间分布.然后，再将这些矢量内边界点的数据输入到现有有限元软件网格自动生成程序来生成网格单元，每一个单元都附有所属介质类别代号.

3.3 第二种二维网格生成方法

数字图像是由一个个正方形像素点组成.因此，每一个正方形像素点就是一个有限元网格或有限差分栅格.将每一正方形像素点的4个角点坐标直接转换为相应矢量空间的物理坐标，得到如图7所示的计算网格.根据每个像素点所属灰色度或者彩色特性和介质类别，在数值计算中赋予该正方形单元的相应种类和本构模型参数.

图7 正方形像素点数据结构转换为正方形单元网格矢量结构(Chen et al.,2004a)(a)正方形像素点;(b)正方形单元网格.Fig.7 Square finite element mesh from square pixels of digital image (Chen et al.,2004a)(a)Square pixels;(b)Square finite element mesh.

3.4 三维数值网格方法

如图8所示，在上述第二种正方形网格自动形成方法基础上，建立了一种基于细观非均质分布的三维空间单元网格生成方法.首先在花岗岩试样表面画下高度线，再用扫描照相仪获取顶面细观结构数字图像，然后磨去顶面指定厚度薄层，再获取新一顶面细观结构数字图像.其结果如图8a所示.

重复该方法，到达设定高度，使每一顶面细观结构像素转换成带有材料属性的正方形网格.将正方形单元网格沿高度方向向下等厚度延伸，每一正方形单元转变成高度等于磨去薄层厚度的长方体单元，再将长方体单元网格沿高度方向与下一层长方体单元相连，形成此花岗岩细观三维空间长方体单元网格.其结果如图8b所示.

4 真实非均质岩土力学响应的一些重要规律

运用这套方法，准确测量和计算分析了一些典型实验室岩土试验的力学响应和破坏过程.这些力学试验包括巴西圆盘间接拉伸试验、单轴压缩试验和单轴拉伸试验.这些数值力学试验分别在二维平面应力和三维空间应力条件下进行.通过与相同大小、相同加载的均质化材料计算结果对比，获得了岩石矿物和混凝土骨料的细观介质实际空间分布对这些试验结果的微观和宏观影响.

4.1 拉压应力场的短距高低变化

图9是沥青混凝土材料的巴西圆盘试验纯弹性数值模拟结果.同均质材料模型相比，细观非均质材料模型的应力场在空间上变化极大.由图9b可见，沿加载中轴线上的环向正应力存在短距离内的高低起伏变化.特别地，局部拉张应力峰值可增大到均质材料模型恒定拉张应力值的3倍.这个改变也导致了在起始破坏单元点、破坏扩展途径和抗破坏能力方面非均质材料与均质材料存在极大的差别 (Chen et al.,2004a,2007;陈沙等,2005,2006;岳中琦,2006).

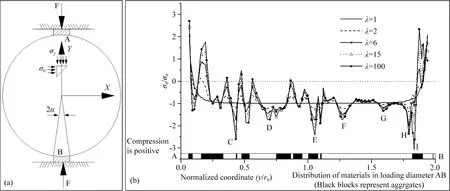
图9 考虑细观非均质混凝土巴西圆盘试验的弹性数值模拟结果(Yue et al.,2003a)(a)巴西圆盘试验；(b)沿加载中轴线环向正应力的分布.Fig.9 Numerical Brazilian test results of meso-heterogeneous asphalt concrete (Yue et al.,2003a)(a)The Brazilian test model;(b)The normal hoop stress along the loading axis line.

4.2 等价的加权平均弹性模量

图10 是花岗岩材料的巴西圆盘试验弹塑脆性数值模拟结果.石英、长石和云母分别占据图10a中圆盘面积的26%、71%和3%.假设石英、长石和云母的弹性模量分别为90、70和40 GPa，它们的抗拉强度分别为14、11和7 MPa.图10b中的前三个计算方案H1、H2和H3都是均质材料模型：H1具有100%单一石英材料性质参数；H2具有石英、长石和云母的面积加权平均材料参数性质；H3具有100%云母材料性质参数.第四个方案IH考虑了真实细观组分的非均质分布和对应三种矿物材料性质参数.从图10b可见以下这个重要规律：在突发拉张破坏前，弹性位移与载荷的变化关系均呈直线，该直线的坡度代表了对应材料的弹性模量；拥有最大弹性模量的石英方案H1的坡度最大；加权均质方案H2和细观非均质方案IH的坡度相当，位于中等；拥有最小弹性模量的云母方案H3的坡度最小.结果揭示了弹性模量加权平均方法可以预测非均质材料在加载作用下的宏观位移或沉降.

图10 考虑三种造岩矿物实际分布的花岗岩巴西圆盘试验弹塑脆性数值模拟结果(Chen et al.,2004a)(a)花岗岩截面照片；(b)位移与载荷的变化关系.Fig.10 Numerical Brazilian test results of granite with actual heterogeneity of feldspar,quartz and micas (Chen et al.,2004a)(a)Cross-section image of granite;(b)Curves of displacement versus load.

4.3 极大降低的抗拉强度

由图10b的计算结果可见另外一个重要规律.突发拉张破坏发生时，这四个计算方案所对应的加载分别是29.0、24.6、14.5和11.0 kN，所对应的均质材料抗拉强度分别是14.0、11.9、7.0和5.3 MPa.结果揭示，仅占面积3%的低抗拉强度材料云母，在非均质材料拉张破坏起到决定性作用.非均质材料在拉张破坏时所对应的均质材料抗拉强度(5.3 MPa)也仅仅是方案H3云母抗拉强度(7.0 MPa)的75.9%，是方案H2的面积加权抗拉强度(11.7 MPa)的45.4%.方案H2的面积加权抗拉强度(11.7 MPa)与在拉张破坏时所对应的均质材料抗拉强度(11.9 MPa)相当一致，相差仅0.18 MPa(1.5%).

以上三个重要规律也体现于考虑花岗岩细观矿物非均质分布的单轴拉伸或单轴抗压试验弹塑脆性数值试验结果(陈沙等,2005).它们同样地体现在如图11所示的考虑花岗岩细观矿物非均质分布的三维单轴抗压试验弹塑脆性数值试验结果(Chen et al.,2004a,2007;陈沙等,2005,2006;岳中琦,2006).

图11 考虑花岗岩细观矿物非均质分布的三维压缩试验弹塑脆性数值试验(陈沙等,2006)(a)多层长方体单元网格；(b)数值单轴抗压试验的应力-应变曲线.Fig.11 Three-dimensional numerical compression test results of granite with meso-heterogeneity of feldspar,quartz and mica (Chen et al.,2006)(a)Multi-layered three-dimensional rectangular element mesh;(b)Stress-strain curves of numerical uniaxial compression test.

4.4 渗透绕过岩块流动

图12是细观非均质土石混合体中渗流场的数值模拟结果.可见，土体中渗透流线绕过岩块流动.这种现象的原因在于，土体渗透系数比岩块渗透系数高200倍，地下水难以在低渗透能力的岩块中渗流.

图12 细观非均质土石混合体的渗流场数值模拟结果(Yue et al.,2003b)(a)土石混合体数字图像；(b)流线分布数值结果.Fig.12 Numerical results of seepage in meso-heterogeneous soil and rock mixtures (Yue et al.,2003b)(a)Digital image of soil and rock mixtures;(b)Numerical results of flow nets.

4.5 混凝土内部骨料排列定向规律

通过测量沥青混凝土内部骨料空间分布，岳中琦等(Yue et al.,1995)发现了骨料在水平面上剖面面积比其在竖直面上剖面面积大，定量说明了骨料主要剖面倾向于水平排列.这证明了水平碾压使原来因搅拌而混乱分布的骨料主剖面成大体水平定向排列.通过测量水泥混凝土内部骨料空间分布，岳中琦等也发现了水泥混凝土骨料在水平面上的剖面面积小于其在竖直方向上的剖面面积(Yue，2007；岳中琦，2006).这说明，电动棒竖直插入在骨料、水泥和水混合流体内的振动能导致骨料剖面成大体竖直排列.

5 小结与展望

本文主要介绍了真实细观非均质岩土材料力学响应的数值求解与分析方法体系，将真实细观非均质岩土材料平面图像精准转化为二维和三维数值网格的计算方法，和考虑真实细观非均质岩土材料在经典载荷作用下力学响应的几条重要规律.

随着数字图像和计算机技术广泛和飞速的发展，基于数字图像的真实细观非均质岩土材料力学响应数值方法成本低、方便易学的优势逐渐凸显，在实际需求量大、问题多的岩土工程领域得到了广泛应用.特别地，基于数字图像的岩石、土体、土石混合体、混凝土和它们与数值模拟相结合的研究，近十几年已经迅速地发展起来了.这个方向研究工作的未来发展空间更是极其广阔和重要.

第一，非均质细观材料空间信息的精准获取最为重要.所使用的数字图像获取方法和技术是早期的和简单的.现在可获得更加精准的数字图像技术(如X射线、Computed Tomography(CT)和扫描电镜(SEM))技术，已经大量应用于与该项目相关的研究课题.基于数字图像技术，单一细观和中-细-微观尺度等多尺度非均匀性问题都有了相当深入的研究，考虑非均质岩土材料的液-气-固多相性理论研究也有了发展.

其次，在与数字图像法有效结合的数值计算方法上，虽仅使用了有限元法和有限差分法，但可拓展到离散元法等数值方法.与先进数值计算相结合的这些方法，可以利用各种数值方法的优势来精确模拟相关复杂的实际问题.

第三，由于材料的细观和微观非均质空间分布是大量实际材料的基本性质，数字图像方法与数值计算和模拟方法相结合具有广泛的应用前景，目前仅进行了极其有限的非均质花岗岩和混凝土典型试验的数值试验研究.它们可以被拓展到更加精细问题的数值模拟，这些问题包括三轴试验条件下土样剪切带出现和形成规律、土工合成材料在拉伸试验过程中的应变分布特征、砂土地基重力场离心场承载力试验条件下滑动剪切带位置的形状及局部化问题、土石混合体边坡稳定性、滑坡问题和三维打印重建技术.

总之，基于数字图像的非均质岩土材料力学的数值模拟和分析已经在岩土力学与工程的多个领域有了深入和广泛的发展和应用，产生了不少定量的新方法、新知识和新规律，促进了真实非均质岩土和混凝土材料定量研究与数值计算的进步和发展.

致谢感谢陈沙博士、郑宏教授和谭国焕教授在香港大学的合作研究，感谢研究助理Bekking W和Mori I的早期研究协助，感谢北京大学、建设部综合勘察研究院、Carleton 大学、加拿大国家研究院、加拿大交通部、和乐中国有限公司、香港大学(中国)和香港特别行政区政府研究基金委员会(中国)在不同时期的研究资助.